人教版八年级数学上册第13章节轴对称(全章节)导学案(无答案)
文档属性
| 名称 | 人教版八年级数学上册第13章节轴对称(全章节)导学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 342.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-03 22:28:50 | ||
图片预览



文档简介
13.1.1轴对称
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)理解轴对称图形和两个图形关于某直线对称的概念。
(2)了解轴对称的对称轴,两个图形关于某直线对称的对称轴、对应点。
(3)掌握线段的垂直平分线的概念。
(4)理解和掌握轴对称的性质。
学习重点:轴对称图形和两个图形关于某直线对称的概念
学习难点:轴对称图形和两个图形关于某直线对称的区别与联系。
自学指导:阅读课本P58-60,完成下列各题:
1.预习学案:
(1).如果一个图形沿一条__________折叠,________两旁的部分能够完全________.这个图形就叫做轴对称图形,这条________就是它的 ,这时,我们也说这个图形关于这条_________(成轴) 对称.
(2).一个图形沿着某条直线折叠,如果他能 ( http: / / www.21cnjy.com )够与________重合,那么就说_______关于这条直线对称,这条直线叫做__________,折叠后________叫做对称点.
2.预习思考:
(1)成轴对称与轴对称图形的区别是什么?
图形轴对称的性质是什么?
二.自学检测
1.下面的图形是轴对称图形吗?如果是,指出对称轴。
2.我国的文字非常讲究对称美,分析图中的四个图案,图案( )有别于其余三个图案.
3.如图是我国几家银行的标志,在这几个图案中是轴对称图形的有哪些?它们各有几条对称轴,你能画出来吗?(小组讨论完成)
3、李芳同学球衣上的号码是253,当他把镜子放在号码的正左边时,镜子中的号码是( )
4、观察规律并填空:
5、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
(小组讨论回答)
( http: / / www.21cnjy.com )
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测
1、课本P64习题1、2、3
2、下面哪些选项的右边图形与左边图形成轴对称
3、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等 哪些线段相等
4、找出英文26个大写字母中哪些是轴对称图形?
5、你能举出三个是轴对称图形的汉字吗?
13.1.1 轴对称习题
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
一.选择题:
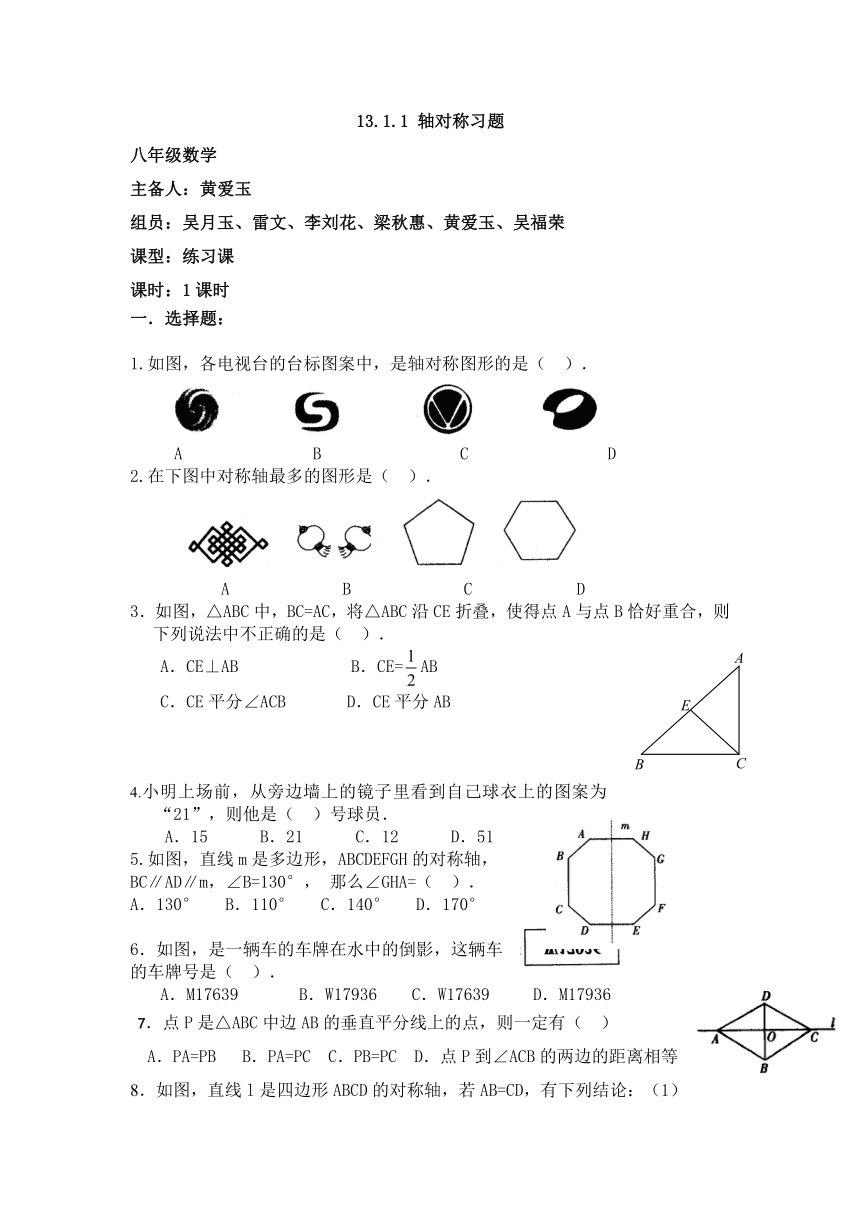
1.如图,各电视台的台标图案中,是轴对称图形的是( ).
A B C D
2.在下图中对称轴最多的图形是( ).
( http: / / / )
A B C D
3.如图,△ABC中,BC=AC,将△ABC沿CE折叠,使得点A与点B恰好重合,则下列说法中不正确的是( ).
A.CE⊥AB B.CE=AB
C.CE平分∠ACB D.CE平分AB
4.小明上场前,从旁边墙上的镜子里看到自己球衣上的图案为“21”,则他是( )号球员.
A.15 B.21 C.12 D.51
5.如图,直线m是多边形,ABCDEFGH的对称轴,
BC∥AD∥m,∠B=130°,那么∠GHA=( ).
A.130° B.110° C.140° D.170°
6.如图,是一辆车的车牌在水中的倒影,这辆车
的车牌号是( ).
M17639 B.W17936 C.W17639 D.M17936
7.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A.PA=PB B.PA=PC C.PB=PC D.点P到∠ACB的两边的距离相等
8.如图,直线l是四边形ABCD的对称 ( http: / / www.21cnjy.com )轴,若AB=CD,有下列结论:(1)AC⊥BD;(2)AB∥CD;(3)AO=CO;(4)AB⊥BC.其中正确的结论有( )个.
A.4 B.3 C.2 D.1
9.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是( )
A.9 B.8 C.7 D.6
二.填空题:
1.观察如下26个英文字母:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
其中是轴对称图形的有_______个.
2.汉字中有许多轴对称图形,请你举出这样的五个汉字: 。
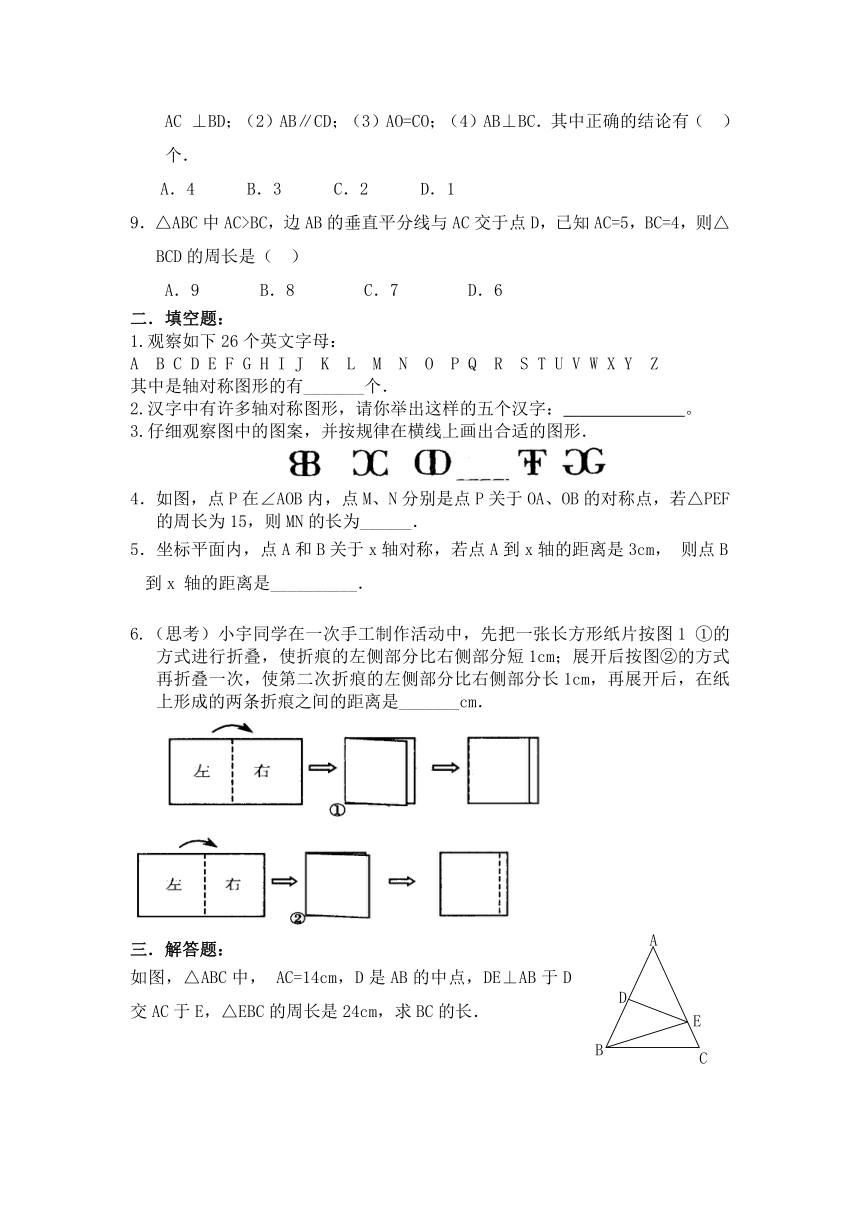
3.仔细观察图中的图案,并按规律在横线上画出合适的图形.
4.如图,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点,若△PEF的周长为15,则MN的长为______.
5.坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm, 则点B到x轴的距离是__________.
6.(思考)小宇同学在一次手工制作 ( http: / / www.21cnjy.com )活动中,先把一张长方形纸片按图1①的方式进行折叠,使折痕的左侧部分比右侧部分短1cm;展开后按图②的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm,再展开后,在纸上形成的两条折痕之间的距离是_______cm.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
三.解答题:
如图,△ABC中, AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,求BC的长.
13.1.2线段的垂直平分线的性质
13.1.2.1线段的垂直平分线的性质与判定
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
掌握线段的垂直平分线的性质与判定,能灵活运用线段的垂直平分线的性质与判定解题
学习重点:线段垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题
学习难点:灵活运用线段垂直平分线性质和判定解题
一:自学指导:阅读课本P61-62,完成下列各题:
预习学案
线段的垂直平分线的性质是 .
线段的垂直平分线的判定是 .
预习思考
如图,已知∠AOB和线段MN,求作一点P,使点P到∠AOB两边的距离相等,且PM=PN. ( http: / / www.21cnjy.com )
自学检测:
1、已知互不平行的两条线段AB, A′B′关于直线l对称,AB, A′B′所在的直线交于点P,判断下列正误。
1)AB=A′B′( ) 2)点P在直线l上( )
3)若A, A′是对称点,则l垂直平分线段A A′( )
4)若B, B′是对称点,则PB=P B′( )
2.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测:
1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
2、如图,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
13.1.2.2画对称轴
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:会画轴对称图形的对称轴
学习重点:轴对称图形的对称轴的画法
学习难点:轴对称图形的对称轴的画法
一:自学指导:阅读课本P62-63,完成下列各题:
预习学案
已知线段AB,求作AB的垂直平分线.
作法:
分别以点 为圆心,以 为半径作弧,两弧相较于C,D两点;
作 ;
为所求作的直线.
预习思考
画出下列图形的对称轴.
二.自学检测
1.试着画出下边两个轴对称图形的对称轴。
2.下面是我们学过的一些几何图形,说出下面图形是不是轴对称图形,并完成下表。
长方形 正方形 三角形 等腰三角形 等边三角形
平行四边形 任意梯形 等腰梯形 圆
图形 长方形 正方形 三角形 等腰三角形 等边三角形 平行 四边形 任意梯形 等腰梯形 圆
对称轴的条数
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测:
1、画出以下图形的对称轴
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.下列图形中:①角,②正方形,③梯形,④圆,⑤菱形,⑥平行四边形,其中是轴对称图形的有( )
A、2个 B、3个 C、4个 D、5个
3:下面的虚线,哪些是图形的对称轴,哪些不是
( http: / / www.21cnjy.com )
3、课本P64练习题3
4、课本P65习题5
13.1 轴对称 练习题
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
一.选择题:
1.如图,我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图中我国四大银行的商标图案中轴对称图形的是( )
① ② ③ ④
A.①②③ B.②③④ C.③④① D.④①②
2.下列图形中,不是轴对称图形的是( )
A.有两个角相等的三角形 B.有一个角为45 的直角三角形
C.有一个内角为30 ,一个内角为120 的三角形 D.有一个内角为30 的直角三角形
3.下列图形中,不是轴对称图形的是( )
A.角 B.等边三角形 C.线段 D.不等边三角形
4.正五角星的对称轴的条数是( )
A.1条 B.2条 C.5条 D.10条
5.下列图形中有4条对称轴的是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
6.已知△ABC与△A1B1C1关于直线MN对称,且BC与B1C1交与直线MN上一点O,则 ( )
A.点O是BC的中点 B.点O是B1C1的中点
C.线段OA与OA1关于直线MN对称 D.以上都不对
二.填空题
7.线段轴是对称图形,它有_______条对称轴.
8.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若CD=4,则点D到AB的距离是__________.
9.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,则∠BAC=____________.
10.△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=115°,则∠EAF=___________.
三.解答题
11.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹
( http: / / www.21cnjy.com )
12.如图,A、B两村在一条小河的的同一侧,要在河边建一水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请将上述两种情况下的自来水厂厂址标出,并保留 ( http: / / www.21cnjy.com )作图痕迹.
.B
A .
(A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
A
B
P
正方形
等边三角形
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)理解轴对称图形和两个图形关于某直线对称的概念。
(2)了解轴对称的对称轴,两个图形关于某直线对称的对称轴、对应点。
(3)掌握线段的垂直平分线的概念。
(4)理解和掌握轴对称的性质。
学习重点:轴对称图形和两个图形关于某直线对称的概念
学习难点:轴对称图形和两个图形关于某直线对称的区别与联系。
自学指导:阅读课本P58-60,完成下列各题:
1.预习学案:
(1).如果一个图形沿一条__________折叠,________两旁的部分能够完全________.这个图形就叫做轴对称图形,这条________就是它的 ,这时,我们也说这个图形关于这条_________(成轴) 对称.
(2).一个图形沿着某条直线折叠,如果他能 ( http: / / www.21cnjy.com )够与________重合,那么就说_______关于这条直线对称,这条直线叫做__________,折叠后________叫做对称点.
2.预习思考:
(1)成轴对称与轴对称图形的区别是什么?
图形轴对称的性质是什么?
二.自学检测
1.下面的图形是轴对称图形吗?如果是,指出对称轴。
2.我国的文字非常讲究对称美,分析图中的四个图案,图案( )有别于其余三个图案.
3.如图是我国几家银行的标志,在这几个图案中是轴对称图形的有哪些?它们各有几条对称轴,你能画出来吗?(小组讨论完成)
3、李芳同学球衣上的号码是253,当他把镜子放在号码的正左边时,镜子中的号码是( )
4、观察规律并填空:
5、参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
(小组讨论回答)
( http: / / www.21cnjy.com )
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测
1、课本P64习题1、2、3
2、下面哪些选项的右边图形与左边图形成轴对称
3、如图,若沿虚线对折,左边部分与右边部分重合,请找出图中A、B、C的对称点,并说出图中有哪些角相等 哪些线段相等
4、找出英文26个大写字母中哪些是轴对称图形?
5、你能举出三个是轴对称图形的汉字吗?
13.1.1 轴对称习题
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
一.选择题:
1.如图,各电视台的台标图案中,是轴对称图形的是( ).
A B C D
2.在下图中对称轴最多的图形是( ).
( http: / / / )
A B C D
3.如图,△ABC中,BC=AC,将△ABC沿CE折叠,使得点A与点B恰好重合,则下列说法中不正确的是( ).
A.CE⊥AB B.CE=AB
C.CE平分∠ACB D.CE平分AB
4.小明上场前,从旁边墙上的镜子里看到自己球衣上的图案为“21”,则他是( )号球员.
A.15 B.21 C.12 D.51
5.如图,直线m是多边形,ABCDEFGH的对称轴,
BC∥AD∥m,∠B=130°,那么∠GHA=( ).
A.130° B.110° C.140° D.170°
6.如图,是一辆车的车牌在水中的倒影,这辆车
的车牌号是( ).
M17639 B.W17936 C.W17639 D.M17936
7.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A.PA=PB B.PA=PC C.PB=PC D.点P到∠ACB的两边的距离相等
8.如图,直线l是四边形ABCD的对称 ( http: / / www.21cnjy.com )轴,若AB=CD,有下列结论:(1)AC⊥BD;(2)AB∥CD;(3)AO=CO;(4)AB⊥BC.其中正确的结论有( )个.
A.4 B.3 C.2 D.1
9.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是( )
A.9 B.8 C.7 D.6
二.填空题:
1.观察如下26个英文字母:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
其中是轴对称图形的有_______个.
2.汉字中有许多轴对称图形,请你举出这样的五个汉字: 。
3.仔细观察图中的图案,并按规律在横线上画出合适的图形.
4.如图,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点,若△PEF的周长为15,则MN的长为______.
5.坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm, 则点B到x轴的距离是__________.
6.(思考)小宇同学在一次手工制作 ( http: / / www.21cnjy.com )活动中,先把一张长方形纸片按图1①的方式进行折叠,使折痕的左侧部分比右侧部分短1cm;展开后按图②的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm,再展开后,在纸上形成的两条折痕之间的距离是_______cm.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
三.解答题:
如图,△ABC中, AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,求BC的长.
13.1.2线段的垂直平分线的性质
13.1.2.1线段的垂直平分线的性质与判定
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
掌握线段的垂直平分线的性质与判定,能灵活运用线段的垂直平分线的性质与判定解题
学习重点:线段垂直平分线的性质和判定,能灵活运用线段的垂直平分线的性质和判定解题
学习难点:灵活运用线段垂直平分线性质和判定解题
一:自学指导:阅读课本P61-62,完成下列各题:
预习学案
线段的垂直平分线的性质是 .
线段的垂直平分线的判定是 .
预习思考
如图,已知∠AOB和线段MN,求作一点P,使点P到∠AOB两边的距离相等,且PM=PN. ( http: / / www.21cnjy.com )
自学检测:
1、已知互不平行的两条线段AB, A′B′关于直线l对称,AB, A′B′所在的直线交于点P,判断下列正误。
1)AB=A′B′( ) 2)点P在直线l上( )
3)若A, A′是对称点,则l垂直平分线段A A′( )
4)若B, B′是对称点,则PB=P B′( )
2.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测:
1.如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
2、如图,△ABC中,AB=AC=18cm,BC= 10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
13.1.2.2画对称轴
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:会画轴对称图形的对称轴
学习重点:轴对称图形的对称轴的画法
学习难点:轴对称图形的对称轴的画法
一:自学指导:阅读课本P62-63,完成下列各题:
预习学案
已知线段AB,求作AB的垂直平分线.
作法:
分别以点 为圆心,以 为半径作弧,两弧相较于C,D两点;
作 ;
为所求作的直线.
预习思考
画出下列图形的对称轴.
二.自学检测
1.试着画出下边两个轴对称图形的对称轴。
2.下面是我们学过的一些几何图形,说出下面图形是不是轴对称图形,并完成下表。
长方形 正方形 三角形 等腰三角形 等边三角形
平行四边形 任意梯形 等腰梯形 圆
图形 长方形 正方形 三角形 等腰三角形 等边三角形 平行 四边形 任意梯形 等腰梯形 圆
对称轴的条数
三.课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四.课堂小测:
1、画出以下图形的对称轴
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.下列图形中:①角,②正方形,③梯形,④圆,⑤菱形,⑥平行四边形,其中是轴对称图形的有( )
A、2个 B、3个 C、4个 D、5个
3:下面的虚线,哪些是图形的对称轴,哪些不是
( http: / / www.21cnjy.com )
3、课本P64练习题3
4、课本P65习题5
13.1 轴对称 练习题
八年级数学
主备人:黄爱玉
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
一.选择题:
1.如图,我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图中我国四大银行的商标图案中轴对称图形的是( )
① ② ③ ④
A.①②③ B.②③④ C.③④① D.④①②
2.下列图形中,不是轴对称图形的是( )
A.有两个角相等的三角形 B.有一个角为45 的直角三角形
C.有一个内角为30 ,一个内角为120 的三角形 D.有一个内角为30 的直角三角形
3.下列图形中,不是轴对称图形的是( )
A.角 B.等边三角形 C.线段 D.不等边三角形
4.正五角星的对称轴的条数是( )
A.1条 B.2条 C.5条 D.10条
5.下列图形中有4条对称轴的是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
6.已知△ABC与△A1B1C1关于直线MN对称,且BC与B1C1交与直线MN上一点O,则 ( )
A.点O是BC的中点 B.点O是B1C1的中点
C.线段OA与OA1关于直线MN对称 D.以上都不对
二.填空题
7.线段轴是对称图形,它有_______条对称轴.
8.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若CD=4,则点D到AB的距离是__________.
9.若D为△ABC的边BC上一点,且AD=BD,AB=AC=CD,则∠BAC=____________.
10.△ABC中,AB、AC的垂直平分线分别交BC于点E、F,若∠BAC=115°,则∠EAF=___________.
三.解答题
11.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹
( http: / / www.21cnjy.com )
12.如图,A、B两村在一条小河的的同一侧,要在河边建一水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?
请将上述两种情况下的自来水厂厂址标出,并保留 ( http: / / www.21cnjy.com )作图痕迹.
.B
A .
(A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
A
B
P
正方形
等边三角形
