人教版八年级数学上册第12章节全等三角形(全章节)导学案(无答案)
文档属性
| 名称 | 人教版八年级数学上册第12章节全等三角形(全章节)导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-03 23:02:13 | ||
图片预览




文档简介
12.1 全等三角形
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)理解全等三角形的概念,能识别全等三角形的对应顶点、对应边、对应角。
(2)掌握全等三角形的性质,并运用性质解决有关的问题。
(3)会用符号表示全等三角形及他们的对应元素,培养大家的符号意识。
一、自学指导:阅读课本P31-32,完成下列各题:
1、能够______________的两个图形叫做全等形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的 ( http: / / www.21cnjy.com )顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、如图所示,△OCA≌△OBD,
对应顶点有:点 和点 ,点 和点 ,点 和点 ;
对应角有: 和 , 和 ,
和 ;
对应边有: 和 , 和 , 和 。
全等三角形的性质:全等三角形的 相等,
全等三角形的 相等。
二、自学检测:
1、如图,已知图中的两个三角形全等,填空:
(1)点A的对应点是 ,
点B的对应点是 ,
点C的对应点是 ;
(2)这两个三角形全等,记作△ABC≌ 。
2、如图,已知图中的两个三角形全等,填空:
(1)OA的对应边是 ,AC的对应边是 ,CO的对应边是
(2)∠A的对应角是 , ∠C的对应角是 ,
∠AOC的对应角是 ;
(3)这两个三角形全等,记作△ACO≌ 。
3、如图,图中有两对三角形全等,填空:
(1)△BOD≌ ;(2)△ACD≌ 。
4、课本32页练习。
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
第1题图 第2题图
1、如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD= 。
2、如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm;
(2)若∠A =50°,∠E=75°,则∠B= ,∠DFE= 。
3、如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
第3题图
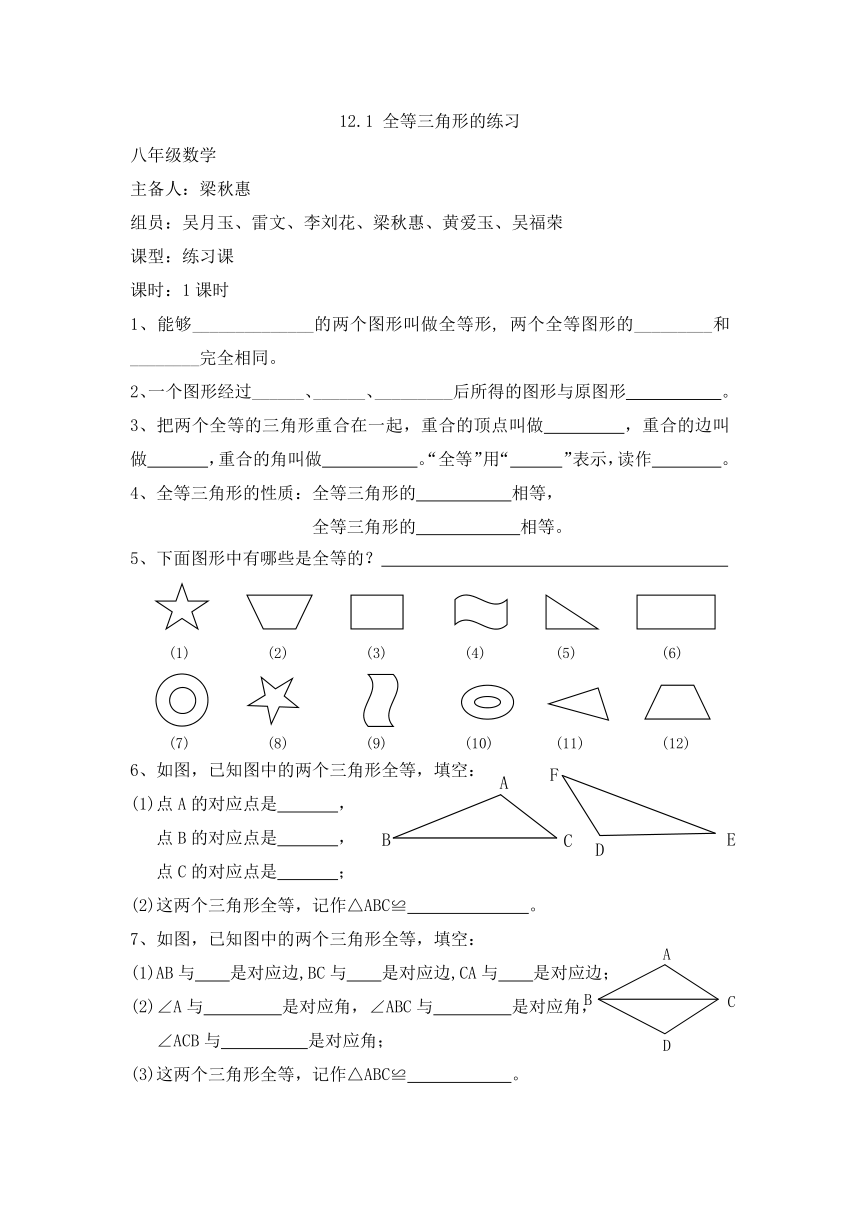
12.1 全等三角形的练习
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
1、能够______________的两个图形叫做全等形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的顶 ( http: / / www.21cnjy.com )点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、全等三角形的性质:全等三角形的 相等,
全等三角形的 相等。
5、下面图形中有哪些是全等的?
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
6、如图,已知图中的两个三角形全等,填空:
(1)点A的对应点是 ,
点B的对应点是 ,
点C的对应点是 ;
(2)这两个三角形全等,记作△ABC≌ 。
7、如图,已知图中的两个三角形全等,填空:
(1)AB与 是对应边,BC与 是对应边,CA与 是对应边;
(2)∠A与 是对应角,∠ABC与 是对应角,
∠ACB与 是对应角;
(3)这两个三角形全等,记作△ABC≌ 。
8、如图,△ABC≌△AEC,∠B=30°,∠ACB=85°。
求出△AEC各内角的度数。
9、如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,求∠C的度数?
12.2 三角形全等的判定(SSS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的SSS判定定理。
(2)会应用判定定理SSS进行简单的推理判定两个三角形全等。
(3)会作一个角等于已知角。
一、复习回顾:
什么是全等三角形?全等三角形有些什么性质?
如图,△ABC≌△DCB那么
相等的边是:
相等的角是:
二、自学指导:阅读课本P35-37,完成下列各题:
(1)已知一个三角形的三条 ( http: / / www.21cnjy.com )边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:
b.以小组为单位,把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的。
c.归纳:三边对应相等的两个三角形 ,简写为“ ”或“ 。
d.用数学语言表述:
在△ABC和△AˊBˊCˊ中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 ( http: / / www.21cnjy.com ) 。判断 ,叫做证明三角形全等。所以“SSS”是证明三角形全等的一个依据。
(2)[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
(3)尺规作图。
已知:∠AOB. 求作:∠DEF,使∠DEF=∠AOB。
作法:
1
2
3
4
三、自学检测:
1、如图,已知AB=CD,AD=BC,则 ≌ ,
≌
2、课本37页练习。
四、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
五、课堂小测:
1、如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
2、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
12.2 三角形全等的判定(SAS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的SAS判定定理。
(2)会应用判定定理SAS进行简单的推理判定两个三角形全等。
一、自学指导:阅读课本P37-39,完成下列各题:
探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵
∴△ABC≌
[例]如图,有一池塘,要测池塘两端 ( http: / / www.21cnjy.com )A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B。连接AC并延长到点D,使CD=CA。连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A,B的距离。为什么?
探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
自学检测:
1、如图,AD⊥BC,D为BC的中点,那么结论正确的有
A、△ABD≌△ACD
B、∠B=∠C
C、AD平分∠BAC
D、△ABC是等边三角形
2、课本39页练习。
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
1、如图,已知OA=OB,再加个条件 ,
就得到△AOC≌△BOD。
2、 如图,AC=BD,∠1= ∠2,求证:BC=AD.
3、 如图,AC=BD,BC=AD,求证:∠1= ∠2.
12.2 三角形全等的判定(SSS、SAS)的练习
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
1、三边对应相等的两个三角形 ,简写为“ ”或“ 。
用数学语言表述全等三角形判定(一):
在△ABC和△AˊBˊCˊ中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 。所以“SSS”是证明三角形全等的一个依据。
2、两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
用数学语言表述全等三角形判定(二):
在△ABC和中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 。所以“SAS”是证明三角形全等的一个依据。
3、如右图已知:AE=DE,EB=EC,AB=CD, ∠ACB=30°。
求:∠DBC 的度数?
解:∵AE=DE, = (已知)
∴AE+EC= + (等式的性质)
即 =BD
在△ABC和△DBC中:
AB= ( )
=BD(已证)
BC= ( ),
∴△ ≌△ ( )
∴∠ACB =∠ (全等三角形 相等)
∵∠ACB =30°( )
∴∠DBC = °( )
4、如图,已知:AD∥BC,AD=CB,AE=CF.
求证:∠D=∠B.
证明:∵AD∥BC,
∴∠A=∠ (两直线平行, 相等).
∵AE=CF
∴AF=
在△AFD和△CEB中,
∴△AFD≌△CEB( )
∴ =
5、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
6、 如图,AC=BD,BC=AD,求证:∠C=∠D
7、 如图,AC=BD,BC=AD,求证:∠A=∠B
12.2 三角形全等的判定(ASA,AAS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的ASA,AAS判定定理。
(2)会应用判定定理ASA,AAS进行简单的推理判定两个三角形全等。
一、自学指导:阅读课本P39-41,完成下列各题:
探究一:两角和它们的夹边对应相等的两个三角形是否全等?
(1)动手试一试。
已知:△ABC
求作:△,使=∠B, =∠C,=BC,(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(三)
在△ABC和中,
∵
∴△ABC≌
探究二:两角和其中一角的对边对应相等的两三角形是否全等?
(1)如图,在△ABC和△DEF中,∠A=∠ ( http: / / www.21cnjy.com )D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用前面学过的判定方法来证明你的结论吗?
(2)归纳;由上面的证明可以得出全等三角形判定(四):
两个角和其中一角的对边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(3)用数学语言表述全等三角形判定(四)
在△ABC和中,
∵
∴△ABC≌
自学检测:
1、满足下列哪种条件时,就能判定△ABC≌△DEF ( )
A. AB=DE,BC=EF, ∠A=∠D B. AB=DE,BC=EF, ∠C=∠F
C. ∠A=∠D,AC=EF, ∠C=∠F D. ∠A=∠D,AB=DE, ∠B=∠E
2、如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:( )
A. ∠B=∠E B.ED=BC
C. AB=EF D.AF=CD
3、已知:如图AB是∠CAD的平分线,∠C=∠D.
求证:BC=BD.
证明:∵AB是∠CAD的平分线
∴∠ =∠
在△ABC和△ABD中,
∴△ABC≌△ABD( )
∴ =
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
1、如图,已知AB∥DC,AD∥BC。
求证:△ABD≌△CDB。
证明:
∵AB∥DC,
∴∠ =∠
∵AD∥BC,
∴∠ =∠
在△ABD和△CDB中,
∴△ABD≌△CDB( )
2、已知,如图AB∥DC,OB=OD, 求证:OA=OC。
3、如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
12.2 三角形全等的判定(HL)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定直角三角形全等的HL判定定理。
(2)会应用判定定理HL进行简单的推理判定两个三角形全等。
一、复习回顾:
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,
斜边是 。
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF ( http: / / www.21cnjy.com ),AC=DF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
二、自学指导:阅读课本P41-42,完成下列各题:
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC。(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的 ( http: / / www.21cnjy.com )三角形,所以不仅有一般三角形判定全等的方法 “ ”、“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
三、自学检测:
1、如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
2、判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF
∴BF=CE
在Rt△ 和Rt△ 中
∵
∴ ≌ ( )
∴ =
∴ (内错角相等,两直线平行)
四、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
五、课堂小测:
1、已知:如图,△ABC中,AB=AC,AD是高,则______≌______。
依据是______,BD=______,∠BAD=______.
2、已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.
求证:DF=AE.
证明:∵CE=BF,
∴______=______
∵DF⊥BC,AE⊥BC,
∴∠CFD=___________=90°
在Rt△CDF和Rt△BAE中,
____________
____________
∴Rt△______≌Rt△______(HL).
∴DF=AE.
全等三角形的练习题
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
知识点:
全等三角形概念:
能够 的两个三角 ( http: / / www.21cnjy.com )形叫做全等三角形。把两个全等的三角形重合在一起, 叫做对应顶点, 叫做对应边, 叫做对应角。
全等三角形的表示方法:
“全等”用“ ”表示,读作“ ”,记两个三角形全等时,通常把对应顶点的字母写在 上。
寻找全等三角形的对应边和对应角:
两个全等三角形的对应角所对的边是对应边,两个对应角所夹的边是对应边;
两个全等三角形的对应边所对的角是对应角,两个对应边所夹的角是对应角;
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
两个全等三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
全等三角形性质:
(1)全等三角形的对应边、 相等;
(2)全等三角形对应边上的中线相等、对应边上的 相等、对应角上的
相等;
(3)全等三角形的周长相等、 相等。
三角形全等的判定方法:
(1) 对应相等的两个三角形全等(简称“SSS”或“ ”)
(2) 对应相等的两个三角形全等(简称“SAS”或“ ”)
(3) 对应相等的两个三角形全等(简称“ASA”或“ ”)
(4) 和其中一个角的 对应相等的两个三角形全等(简称“AAS”或“ ”)
(5) 对应相等的两个直角三角形全等(简称“HL”或“ ”)
全等三角形判定方法的选择:
已知两边对应相等:
A.证第三边相等,再用SSS证全等;
B.证已知边的夹角相等,再用SAS证全等。
(2)已知一角及其邻边相等:
A.证已知角的另一邻边相等,再用SAS证全等;
B.证已知边的另一邻角相等,再用ASA证全等;
C.证已知边的对角相等,再用AAS证全等。
(3)已知一角及其对边相等:
证另一角相等,再用AAS证全等。
(4)已知两角对应相等:
A. 证其夹边相等,再用ASA证全等;
B. 证一已知角的对边相等,再用AAS证全等。
练习:
1、如图,△ABC≌△CDA,AB和C ( http: / / www.21cnjy.com )D,BC和DA是对应边。写出其他对应边及对应角。
2、如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边。写出其他对应边及对应角。
3、填“一定”或“不一定”:
(1)两边对应相等的两个三角形 全等;
(2)一边一角对应相等的两个三角形 全等;
(3)两角对应相等的两个三角形 全等;
(4)三边对应相等的两个三角形 全等;
(5)两边和它们的夹角对应相等的两个三角形 全等;
(6)两边和其中一边的对角对应相等的两个三角形 全等;
(7)两角和它们的夹边对应相等的两个三角形 全等;
(8)两角和其中一角的对边对应相等的两个三角形 全等;
(9)三角对应相等的两个三角形 全等.
4、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
5、如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
6、已知,如图AB∥DC,OB=OD, 求证:OA=OC。
7、如图:已知AB=AD,AC=AE,求证:﹙1﹚△ABC≌△ADE ;﹙2﹚∠D=∠B。
8、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:测验课
课时:1课时
全等三角形的测试题
时间:45分钟 满分:100分
班别: 姓名: 座号: 得分:
一、选择题(每小题5分,6小题共30分)
1、已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
2、下列命题中:⑴形状相同的两个三 ( http: / / www.21cnjy.com )角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( )
A.3个 B.2个 C.1个 D.0个
3、下列条件中,不能判定△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠A=∠A′,AC=A′C′
B.AB=A′B′,∠A=∠A′,∠B=∠B′
C.AB=A′B′,∠A=∠A′,∠C=∠C′
D.∠A=∠A′,∠B=∠B′,∠C=∠C′
4、根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3cm,BC=4cm,AC=8cm
B. AB=4cm,BC=3cm,∠A=30°
C. ∠A=60°,∠B=45°,AB=4cm
D.∠C=90°, AB=6cm
第5题图 第6题图
5、如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC
6、如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )
A.150° B.40° C.80° D.90°
二、填空题(每小题5分,4小题共20分)
第7题图 第8题图 第9题图
7、如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对。
8、如图,在△ABC中,AB=AC,BE、CF是中线,则由 可得△AFC≌△AEB。
9、如图,AB=CD,AD=BC,O为B ( http: / / www.21cnjy.com )D中点,过O点作直线与DA、BC延长线交于E、F,若∠ADB=60°,EO=10,则∠DBC= ,FO= 。
10、如图,AD,A′D′分别是锐角 ( http: / / www.21cnjy.com )三角形ABC和锐角三角形A′B′C′中BC,B′C′边上的高,且AB=A′B′,AD=A′D′.若使△ABC≌△A′B′C′,请你补充条件________.(填写一个你认为适当的条件即可)
三、解答题(第11题8分,12、13、14题各10分,15题12分)
11、已知:△ABC
求作:△A′B′C′,使△ABC≌△A′B′C′。(保留作图痕迹)
12、如图,AC=BD,BC=AD,求证:∠1= ∠2。
13、已知:点D在AB上,点E在AC上,∠BAO=∠CAO ,BE⊥AC, CD⊥AB,相交于点O,AB=AC,求证:BD=CE。
14、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB。
15、如图:AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F。求证:DE=DF。
B
D
O
A
C
A
B
C
D
O
A
C
D
B
A F C D
1
2
E
B
A
B
C
A1
B1
C1
A
B
D
C
A
D
B
C
E
F
A
B
C
D
A′
B′
D′
C′
D
F
C
A
B
E
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)理解全等三角形的概念,能识别全等三角形的对应顶点、对应边、对应角。
(2)掌握全等三角形的性质,并运用性质解决有关的问题。
(3)会用符号表示全等三角形及他们的对应元素,培养大家的符号意识。
一、自学指导:阅读课本P31-32,完成下列各题:
1、能够______________的两个图形叫做全等形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的 ( http: / / www.21cnjy.com )顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、如图所示,△OCA≌△OBD,
对应顶点有:点 和点 ,点 和点 ,点 和点 ;
对应角有: 和 , 和 ,
和 ;
对应边有: 和 , 和 , 和 。
全等三角形的性质:全等三角形的 相等,
全等三角形的 相等。
二、自学检测:
1、如图,已知图中的两个三角形全等,填空:
(1)点A的对应点是 ,
点B的对应点是 ,
点C的对应点是 ;
(2)这两个三角形全等,记作△ABC≌ 。
2、如图,已知图中的两个三角形全等,填空:
(1)OA的对应边是 ,AC的对应边是 ,CO的对应边是
(2)∠A的对应角是 , ∠C的对应角是 ,
∠AOC的对应角是 ;
(3)这两个三角形全等,记作△ACO≌ 。
3、如图,图中有两对三角形全等,填空:
(1)△BOD≌ ;(2)△ACD≌ 。
4、课本32页练习。
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
第1题图 第2题图
1、如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD= 。
2、如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm;
(2)若∠A =50°,∠E=75°,则∠B= ,∠DFE= 。
3、如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
第3题图
12.1 全等三角形的练习
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
1、能够______________的两个图形叫做全等形, 两个全等图形的_________和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的顶 ( http: / / www.21cnjy.com )点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。
4、全等三角形的性质:全等三角形的 相等,
全等三角形的 相等。
5、下面图形中有哪些是全等的?
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
6、如图,已知图中的两个三角形全等,填空:
(1)点A的对应点是 ,
点B的对应点是 ,
点C的对应点是 ;
(2)这两个三角形全等,记作△ABC≌ 。
7、如图,已知图中的两个三角形全等,填空:
(1)AB与 是对应边,BC与 是对应边,CA与 是对应边;
(2)∠A与 是对应角,∠ABC与 是对应角,
∠ACB与 是对应角;
(3)这两个三角形全等,记作△ABC≌ 。
8、如图,△ABC≌△AEC,∠B=30°,∠ACB=85°。
求出△AEC各内角的度数。
9、如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,求∠C的度数?
12.2 三角形全等的判定(SSS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的SSS判定定理。
(2)会应用判定定理SSS进行简单的推理判定两个三角形全等。
(3)会作一个角等于已知角。
一、复习回顾:
什么是全等三角形?全等三角形有些什么性质?
如图,△ABC≌△DCB那么
相等的边是:
相等的角是:
二、自学指导:阅读课本P35-37,完成下列各题:
(1)已知一个三角形的三条 ( http: / / www.21cnjy.com )边长分别为6cm、8cm、10cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
a.作图方法:
b.以小组为单位,把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的。
c.归纳:三边对应相等的两个三角形 ,简写为“ ”或“ 。
d.用数学语言表述:
在△ABC和△AˊBˊCˊ中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 ( http: / / www.21cnjy.com ) 。判断 ,叫做证明三角形全等。所以“SSS”是证明三角形全等的一个依据。
(2)[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
(3)尺规作图。
已知:∠AOB. 求作:∠DEF,使∠DEF=∠AOB。
作法:
1
2
3
4
三、自学检测:
1、如图,已知AB=CD,AD=BC,则 ≌ ,
≌
2、课本37页练习。
四、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
五、课堂小测:
1、如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
2、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ △ ADE。
12.2 三角形全等的判定(SAS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的SAS判定定理。
(2)会应用判定定理SAS进行简单的推理判定两个三角形全等。
一、自学指导:阅读课本P37-39,完成下列各题:
探究一:两边和它们的夹角对应相等的两个三角形是否全等?
(1)动手试一试
已知:△ABC
求作:,使,,:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(二):
两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(二)
在△ABC和中,
∵
∴△ABC≌
[例]如图,有一池塘,要测池塘两端 ( http: / / www.21cnjy.com )A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B。连接AC并延长到点D,使CD=CA。连接BC并延长到点E,使CE=CB。连接DE,那么量出DE的长就是A,B的距离。为什么?
探究二:两边及其一边的对角对应相等的两个三角形是否全等?
通过画图或实验可以得出:
自学检测:
1、如图,AD⊥BC,D为BC的中点,那么结论正确的有
A、△ABD≌△ACD
B、∠B=∠C
C、AD平分∠BAC
D、△ABC是等边三角形
2、课本39页练习。
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
1、如图,已知OA=OB,再加个条件 ,
就得到△AOC≌△BOD。
2、 如图,AC=BD,∠1= ∠2,求证:BC=AD.
3、 如图,AC=BD,BC=AD,求证:∠1= ∠2.
12.2 三角形全等的判定(SSS、SAS)的练习
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
1、三边对应相等的两个三角形 ,简写为“ ”或“ 。
用数学语言表述全等三角形判定(一):
在△ABC和△AˊBˊCˊ中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 。所以“SSS”是证明三角形全等的一个依据。
2、两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”)
用数学语言表述全等三角形判定(二):
在△ABC和中,
∵
∴△ABC≌
用上面的规律可以判断两个三角形 。所以“SAS”是证明三角形全等的一个依据。
3、如右图已知:AE=DE,EB=EC,AB=CD, ∠ACB=30°。
求:∠DBC 的度数?
解:∵AE=DE, = (已知)
∴AE+EC= + (等式的性质)
即 =BD
在△ABC和△DBC中:
AB= ( )
=BD(已证)
BC= ( ),
∴△ ≌△ ( )
∴∠ACB =∠ (全等三角形 相等)
∵∠ACB =30°( )
∴∠DBC = °( )
4、如图,已知:AD∥BC,AD=CB,AE=CF.
求证:∠D=∠B.
证明:∵AD∥BC,
∴∠A=∠ (两直线平行, 相等).
∵AE=CF
∴AF=
在△AFD和△CEB中,
∴△AFD≌△CEB( )
∴ =
5、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC
6、 如图,AC=BD,BC=AD,求证:∠C=∠D
7、 如图,AC=BD,BC=AD,求证:∠A=∠B
12.2 三角形全等的判定(ASA,AAS)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定三角形全等的ASA,AAS判定定理。
(2)会应用判定定理ASA,AAS进行简单的推理判定两个三角形全等。
一、自学指导:阅读课本P39-41,完成下列各题:
探究一:两角和它们的夹边对应相等的两个三角形是否全等?
(1)动手试一试。
已知:△ABC
求作:△,使=∠B, =∠C,=BC,(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述全等三角形判定(三)
在△ABC和中,
∵
∴△ABC≌
探究二:两角和其中一角的对边对应相等的两三角形是否全等?
(1)如图,在△ABC和△DEF中,∠A=∠ ( http: / / www.21cnjy.com )D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用前面学过的判定方法来证明你的结论吗?
(2)归纳;由上面的证明可以得出全等三角形判定(四):
两个角和其中一角的对边对应相等的两个三角形 (可以简写成“ ”或“ ”)
(3)用数学语言表述全等三角形判定(四)
在△ABC和中,
∵
∴△ABC≌
自学检测:
1、满足下列哪种条件时,就能判定△ABC≌△DEF ( )
A. AB=DE,BC=EF, ∠A=∠D B. AB=DE,BC=EF, ∠C=∠F
C. ∠A=∠D,AC=EF, ∠C=∠F D. ∠A=∠D,AB=DE, ∠B=∠E
2、如图所示,已知∠A=∠D,∠1=∠2,那么要
得到△ABC≌△DEF,还应给出的条件是:( )
A. ∠B=∠E B.ED=BC
C. AB=EF D.AF=CD
3、已知:如图AB是∠CAD的平分线,∠C=∠D.
求证:BC=BD.
证明:∵AB是∠CAD的平分线
∴∠ =∠
在△ABC和△ABD中,
∴△ABC≌△ABD( )
∴ =
三、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
四、课堂小测:
1、如图,已知AB∥DC,AD∥BC。
求证:△ABD≌△CDB。
证明:
∵AB∥DC,
∴∠ =∠
∵AD∥BC,
∴∠ =∠
在△ABD和△CDB中,
∴△ABD≌△CDB( )
2、已知,如图AB∥DC,OB=OD, 求证:OA=OC。
3、如图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
12.2 三角形全等的判定(HL)
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:新授课
课时:1课时
学习目标:
(1)能自己试验探索出判定直角三角形全等的HL判定定理。
(2)会应用判定定理HL进行简单的推理判定两个三角形全等。
一、复习回顾:
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,
斜边是 。
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
②若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF ( http: / / www.21cnjy.com ),AC=DF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
二、自学指导:阅读课本P41-42,完成下列各题:
如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△, 使=90°, =AB, =BC。(不写作法,保留作图痕迹)
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的 ( http: / / www.21cnjy.com )三角形,所以不仅有一般三角形判定全等的方法 “ ”、“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
三、自学检测:
1、如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
2、判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF
∴BF=CE
在Rt△ 和Rt△ 中
∵
∴ ≌ ( )
∴ =
∴ (内错角相等,两直线平行)
四、课堂小结:通过这节课的学习,你有什么收获?还有什么疑惑吗?
五、课堂小测:
1、已知:如图,△ABC中,AB=AC,AD是高,则______≌______。
依据是______,BD=______,∠BAD=______.
2、已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.
求证:DF=AE.
证明:∵CE=BF,
∴______=______
∵DF⊥BC,AE⊥BC,
∴∠CFD=___________=90°
在Rt△CDF和Rt△BAE中,
____________
____________
∴Rt△______≌Rt△______(HL).
∴DF=AE.
全等三角形的练习题
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:练习课
课时:1课时
知识点:
全等三角形概念:
能够 的两个三角 ( http: / / www.21cnjy.com )形叫做全等三角形。把两个全等的三角形重合在一起, 叫做对应顶点, 叫做对应边, 叫做对应角。
全等三角形的表示方法:
“全等”用“ ”表示,读作“ ”,记两个三角形全等时,通常把对应顶点的字母写在 上。
寻找全等三角形的对应边和对应角:
两个全等三角形的对应角所对的边是对应边,两个对应角所夹的边是对应边;
两个全等三角形的对应边所对的角是对应角,两个对应边所夹的角是对应角;
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
两个全等三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
全等三角形性质:
(1)全等三角形的对应边、 相等;
(2)全等三角形对应边上的中线相等、对应边上的 相等、对应角上的
相等;
(3)全等三角形的周长相等、 相等。
三角形全等的判定方法:
(1) 对应相等的两个三角形全等(简称“SSS”或“ ”)
(2) 对应相等的两个三角形全等(简称“SAS”或“ ”)
(3) 对应相等的两个三角形全等(简称“ASA”或“ ”)
(4) 和其中一个角的 对应相等的两个三角形全等(简称“AAS”或“ ”)
(5) 对应相等的两个直角三角形全等(简称“HL”或“ ”)
全等三角形判定方法的选择:
已知两边对应相等:
A.证第三边相等,再用SSS证全等;
B.证已知边的夹角相等,再用SAS证全等。
(2)已知一角及其邻边相等:
A.证已知角的另一邻边相等,再用SAS证全等;
B.证已知边的另一邻角相等,再用ASA证全等;
C.证已知边的对角相等,再用AAS证全等。
(3)已知一角及其对边相等:
证另一角相等,再用AAS证全等。
(4)已知两角对应相等:
A. 证其夹边相等,再用ASA证全等;
B. 证一已知角的对边相等,再用AAS证全等。
练习:
1、如图,△ABC≌△CDA,AB和C ( http: / / www.21cnjy.com )D,BC和DA是对应边。写出其他对应边及对应角。
2、如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边。写出其他对应边及对应角。
3、填“一定”或“不一定”:
(1)两边对应相等的两个三角形 全等;
(2)一边一角对应相等的两个三角形 全等;
(3)两角对应相等的两个三角形 全等;
(4)三边对应相等的两个三角形 全等;
(5)两边和它们的夹角对应相等的两个三角形 全等;
(6)两边和其中一边的对角对应相等的两个三角形 全等;
(7)两角和它们的夹边对应相等的两个三角形 全等;
(8)两角和其中一角的对边对应相等的两个三角形 全等;
(9)三角对应相等的两个三角形 全等.
4、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
5、如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
6、已知,如图AB∥DC,OB=OD, 求证:OA=OC。
7、如图:已知AB=AD,AC=AE,求证:﹙1﹚△ABC≌△ADE ;﹙2﹚∠D=∠B。
8、如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN
八年级数学
主备人:梁秋惠
组员:吴月玉、雷文、李刘花、梁秋惠、黄爱玉、吴福荣
课型:测验课
课时:1课时
全等三角形的测试题
时间:45分钟 满分:100分
班别: 姓名: 座号: 得分:
一、选择题(每小题5分,6小题共30分)
1、已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )
A.50° B.80° C.50°或80° D.40°或65°
2、下列命题中:⑴形状相同的两个三 ( http: / / www.21cnjy.com )角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( )
A.3个 B.2个 C.1个 D.0个
3、下列条件中,不能判定△ABC≌△A′B′C′的是( )
A.AB=A′B′,∠A=∠A′,AC=A′C′
B.AB=A′B′,∠A=∠A′,∠B=∠B′
C.AB=A′B′,∠A=∠A′,∠C=∠C′
D.∠A=∠A′,∠B=∠B′,∠C=∠C′
4、根据下列已知条件,能画出唯一△ABC的是( )
A.AB=3cm,BC=4cm,AC=8cm
B. AB=4cm,BC=3cm,∠A=30°
C. ∠A=60°,∠B=45°,AB=4cm
D.∠C=90°, AB=6cm
第5题图 第6题图
5、如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC
6、如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )
A.150° B.40° C.80° D.90°
二、填空题(每小题5分,4小题共20分)
第7题图 第8题图 第9题图
7、如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对。
8、如图,在△ABC中,AB=AC,BE、CF是中线,则由 可得△AFC≌△AEB。
9、如图,AB=CD,AD=BC,O为B ( http: / / www.21cnjy.com )D中点,过O点作直线与DA、BC延长线交于E、F,若∠ADB=60°,EO=10,则∠DBC= ,FO= 。
10、如图,AD,A′D′分别是锐角 ( http: / / www.21cnjy.com )三角形ABC和锐角三角形A′B′C′中BC,B′C′边上的高,且AB=A′B′,AD=A′D′.若使△ABC≌△A′B′C′,请你补充条件________.(填写一个你认为适当的条件即可)
三、解答题(第11题8分,12、13、14题各10分,15题12分)
11、已知:△ABC
求作:△A′B′C′,使△ABC≌△A′B′C′。(保留作图痕迹)
12、如图,AC=BD,BC=AD,求证:∠1= ∠2。
13、已知:点D在AB上,点E在AC上,∠BAO=∠CAO ,BE⊥AC, CD⊥AB,相交于点O,AB=AC,求证:BD=CE。
14、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB。
15、如图:AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F。求证:DE=DF。
B
D
O
A
C
A
B
C
D
O
A
C
D
B
A F C D
1
2
E
B
A
B
C
A1
B1
C1
A
B
D
C
A
D
B
C
E
F
A
B
C
D
A′
B′
D′
C′
D
F
C
A
B
E
