8.2《正方形的判定》分课时教学设计-----2023-2024 八年级数学 下册 (人教版)
文档属性
| 名称 | 8.2《正方形的判定》分课时教学设计-----2023-2024 八年级数学 下册 (人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
8.2《正方形的判定》分课时教学设计
一、教材分析
《正方形》这节课选自人教版教科书八年级下册第十八章第二节第三课时,正方形是在学生掌握了平行四边形、矩形、菱形、正方形的性质的有关知识,并且具备了观察、操作等活动经验的基础上学习的内容.本节课注重新旧知识的联系与类比,正方形的研究突出体现了从一般到特殊的思路,当矩形的邻边相等时,或者当菱形的一个角变为直角时,它就变成了正方形.在动态演变过程中,引导学生类比矩形和菱形的定义,得出正方形的定义和判定定理,帮助学生理清正方形、菱形、矩形和平行四边形之间的关系,从而落实课标对本节课的要求“理解正方形的概念,以及正方形与平行四边形、菱形、矩形之间的关系;归纳正方形的判定定理。
二、学情分析
学生已经掌握了平行四边形、矩形、菱形的定义性质和判定以及正方形的性质,一部分学生掌握良好具有一定的主动学习和探究学习的能力,但另一部分学生基础一般,加上前面知识不扎实,所以这节课虽然是新课但也会起到对前面知识的复习的作用。通过初步的了解,我发现班上学生上课有较强的表现欲,为了锻炼他们的语言表达能力和动手能力,在本节课的教学过程中,设计了让学生动手探索发现结论,自己组织语言培养说理能力。
三、教学目标
理解并掌握运用正方形的定义;以及如何由平行四边形、矩形、菱形判定为正方形的;会用这些判定方法进行有关的论证和计算。
让学生经历探究正方形判定方法的过程,促使学生学会复习,学会归纳,提高自主学习的意识,培养学生的自学能力。
:通过学习正方形的有关知识,感受正方形的完美特点与和谐之美。让学生感受数学的乐趣,培养学生的主动探索、合作交流的能力和积极主动参与学习的精神。
四、教学重点和难点
教学重点:理解正方形与平行四边形、矩形、菱形之间的关系
教学难点:能熟练运用正方形的性质和判定进行有关的证明和计算.
教法分析
掌握正方形的概念是学好本节课的关键,通过动画演示,让学生认真观察图形变化,类比矩形、菱形的定义得出正方形的定义,通过问题引导,结合框架图和定义,理清正方形与菱形、矩形、平行四边形之间的关系,从而引导学生归纳出正方形的判定.利用图形进行比较教学,学生比较容易理解,同时很清楚各种图形之间的关系,发展学生系统归纳和逻辑思维能力。
六、学法分析
根据学法自由性原则,学生在教师创设的问题情景下,积极思考,自由参与知识的发生、发展、发现的过程,获取新的知识,体现了素质教育中学生学习能力的培养问题。在整个学习过程中,以“自主参与、勇于探索、合作交流”的探索式学法为主,加强学生自己会用类比方法学习,以达到教学的目的。
七、教学媒体与资源的选择与应用
1.在教学过程中,将制作好的课件在西沃白板上展示出来。2.让学生准备矩形纸片两张、小剪刀、三角板、菱形纸片一张。
八、教学过程
教学环节 教学过程
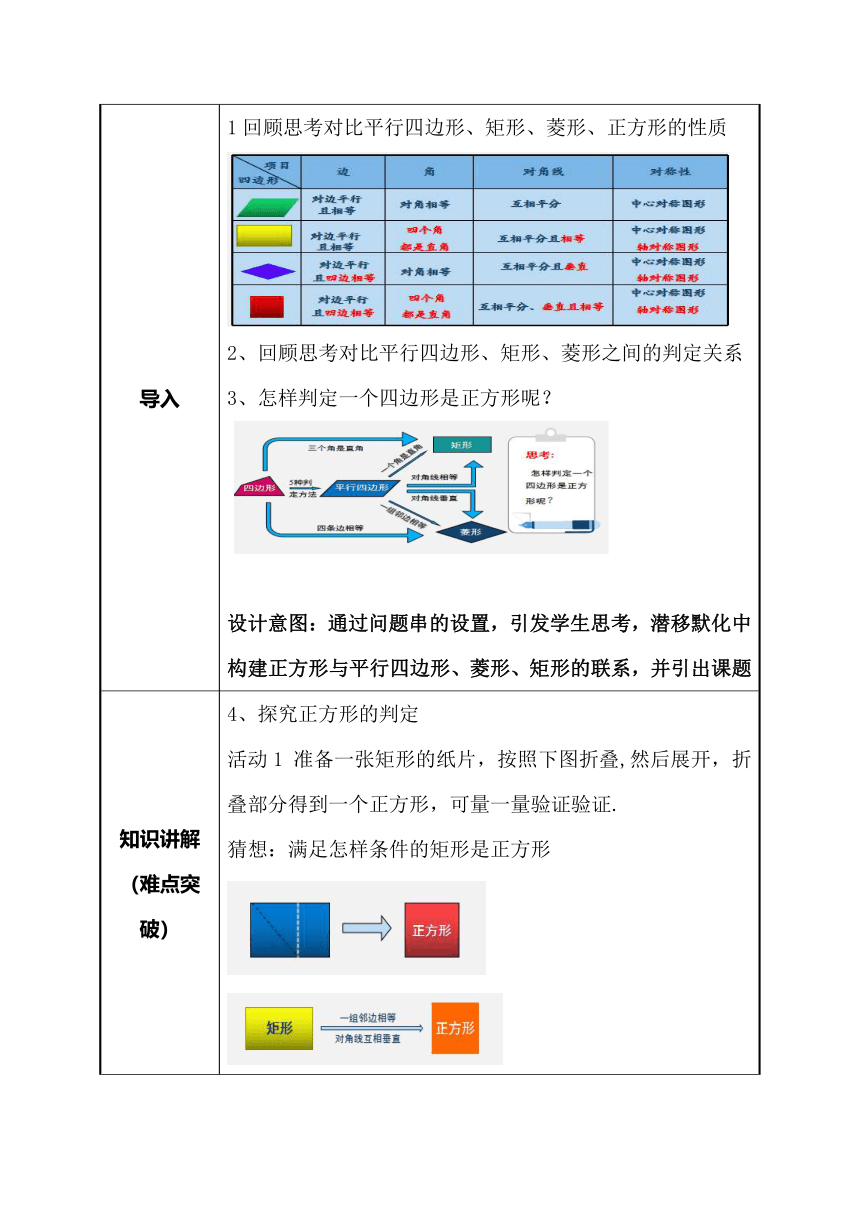
导入 1回顾思考对比平行四边形、矩形、菱形、正方形的性质 2、回顾思考对比平行四边形、矩形、菱形之间的判定关系 3、怎样判定一个四边形是正方形呢? 设计意图:通过问题串的设置,引发学生思考,潜移默化中构建正方形与平行四边形、菱形、矩形的联系,并引出课题
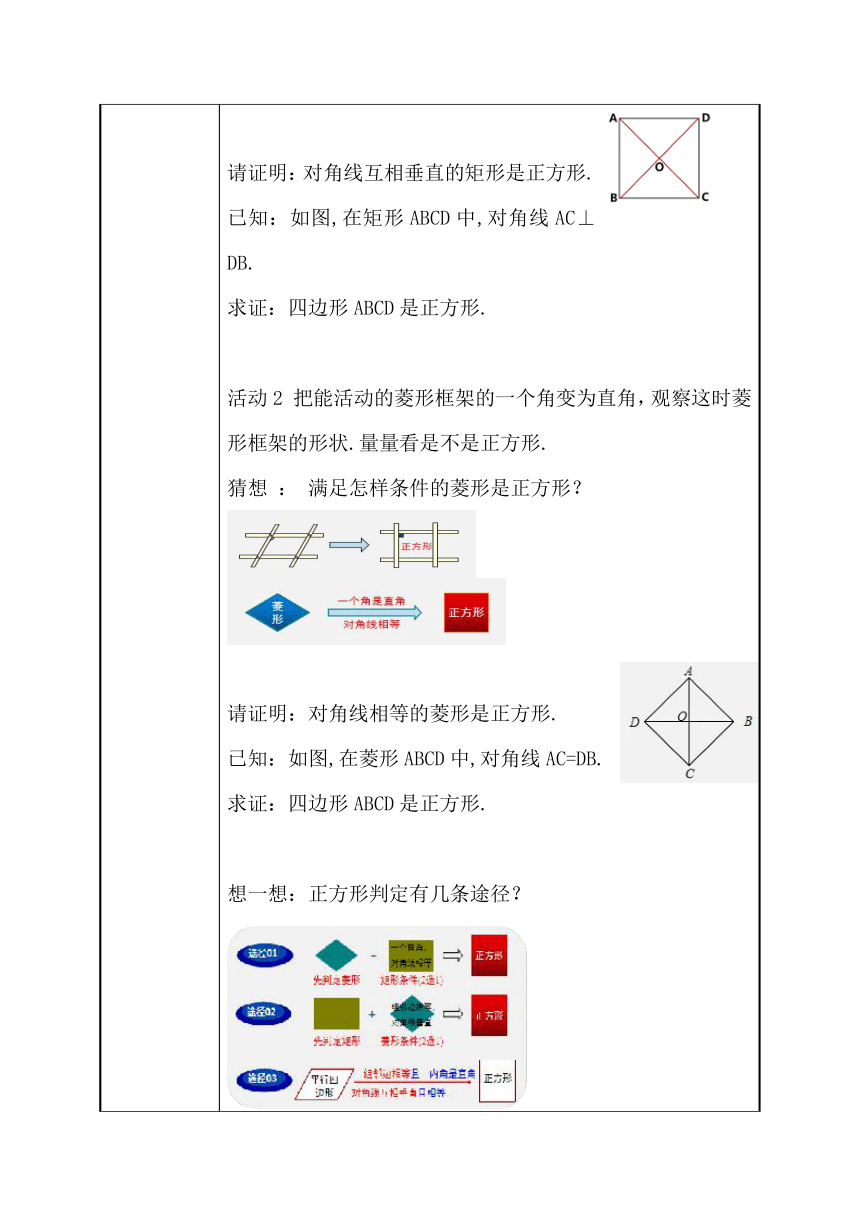
知识讲解 (难点突破) 探究正方形的判定 活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证. 猜想:满足怎样条件的矩形是正方形 请证明:对角线互相垂直的矩形是正方形. 已知:如图,在矩形ABCD中,对角线AC⊥DB. 求证:四边形ABCD是正方形. 活动2 把能活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形. 猜想 : 满足怎样条件的菱形是正方形? 请证明:对角线相等的菱形是正方形. 已知:如图,在菱形ABCD中,对角线AC=DB. 求证:四边形ABCD是正方形. 想一想:正方形判定有几条途径? 设计意图:调动学生已有的学习经验,结合正方形是特殊的矩形和特殊的菱形这一特性,使学生很自然的总结出正方形的判定.从“什么是正方形”,发展到“正方形是什么样的”,让学生自己总结出由菱形到正方形;由矩形到正方形;由平行四边形到正方形三条途径;实现思维方法上的延续与提升,让学生从正方形的性质中感悟做人的道理,提升学生的人为素养. 例题讲解 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形. 已知:如图,正方形ABCD中,对角线AC、BD相交于O. 求证:△ABO,△BCO,△CDO; △DAO是全等的等腰直角三角形 【设计意图】引导学生把几何命题符号化、具体化,进一步明确问题的条件和目标.教师强调书写格式的规范性、严谨性,体会转化思想在解决问题中的作用.
课堂练习 (难点巩固) 1.下列命题正确的是( ) A.四个角都相等的四边形是正方形 B.四条边都相等的四边形是正方形 C.对角线相等的平行四边形是正方形 D.对角线互相垂直的矩形是正方形 2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A.当AB=BC时,四边形ABCD是菱形 B.当AC⊥BD时,四边形ABCD是菱形 C.当∠ABC=90°时,四边形ABCD是矩形 D.当AC=BD时,四边形ABCD是正方形 3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件____________________,可得出该四边形是正方形. 4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号). 5.如图,在四边形ABCD中, AB=BC ,对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD ,垂足分别为M、N. (1) 求证:∠ADB=∠CDB; (2) 若∠ADC=90 ,求证:四边形MPND是正方形. 6.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB. (1)试说明四边形AEDF的形状,并说明理由; (2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么? (3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由. 设计意图:设置由浅入深的分层练习,让学生对正方形的判定进行巩固。最后一题设置第一问平行四边形,第二问为判定菱形,第三问为正方形,切合主题。
小结 平行四边形、矩形、菱形、正方形之间判定的关系 平行四边形、矩形、菱形 、正方形之间的关系 本章学习了哪些四边形?是按照怎样的研究思路进行的? 平行四边形——矩形、菱形——正方形........,按由一般到特殊的思路研究的。 研究各种四边形时,我们的研究内容、研究步骤、研究方法各是怎样的? 研究内容:边、角、对角线的特征 研究步骤:下定义、探性质、研判定。 研究方法: (1)把四边形的问题转化为三角形。 (2)特殊平行四边形类比平行四边形研究。 设计意图:对本节课的知识点进行总结,使学生在头脑中的知识得到强化和提炼。
作业布置 课本p68面,T5、T6、T14 板书设计 1.正方形的判定方法 一组邻边相等的矩形是正方形; 有一个角是直角的菱形是正方形. 正方形性质和判定的应用 【设计意图】清晰明了的板书设计,突出本节课的教学重点,便于学生梳理、归纳正方形的知识框架.
九、教学反思
本节课的教学注意挖掘教材中培养创新意识的素材,在探索正方形判定方法的过程中,充分发挥了学生主体性,让学生经历自主“做数学”的过程---动手折纸,演示自制教具,并播放矩形、菱形、平行四边形的一个角、一组邻边的变化得到正方形课件,成功的达到了学生对正方形直观认识,进而探索出正方形的判定方法。为学生营造一种创新的学习氛围,把学生引上探索问题之路,成功的达到了让学生直观认识正方形的目的。给学生动手操作的机会,变被动为主动学习,引导通过感官的思维去观察、探究、分析知识形成的过程,以此深化知识、更深刻理解知识、主动获取知识,养成良好的学习习惯.
一、教材分析
《正方形》这节课选自人教版教科书八年级下册第十八章第二节第三课时,正方形是在学生掌握了平行四边形、矩形、菱形、正方形的性质的有关知识,并且具备了观察、操作等活动经验的基础上学习的内容.本节课注重新旧知识的联系与类比,正方形的研究突出体现了从一般到特殊的思路,当矩形的邻边相等时,或者当菱形的一个角变为直角时,它就变成了正方形.在动态演变过程中,引导学生类比矩形和菱形的定义,得出正方形的定义和判定定理,帮助学生理清正方形、菱形、矩形和平行四边形之间的关系,从而落实课标对本节课的要求“理解正方形的概念,以及正方形与平行四边形、菱形、矩形之间的关系;归纳正方形的判定定理。
二、学情分析
学生已经掌握了平行四边形、矩形、菱形的定义性质和判定以及正方形的性质,一部分学生掌握良好具有一定的主动学习和探究学习的能力,但另一部分学生基础一般,加上前面知识不扎实,所以这节课虽然是新课但也会起到对前面知识的复习的作用。通过初步的了解,我发现班上学生上课有较强的表现欲,为了锻炼他们的语言表达能力和动手能力,在本节课的教学过程中,设计了让学生动手探索发现结论,自己组织语言培养说理能力。
三、教学目标
理解并掌握运用正方形的定义;以及如何由平行四边形、矩形、菱形判定为正方形的;会用这些判定方法进行有关的论证和计算。
让学生经历探究正方形判定方法的过程,促使学生学会复习,学会归纳,提高自主学习的意识,培养学生的自学能力。
:通过学习正方形的有关知识,感受正方形的完美特点与和谐之美。让学生感受数学的乐趣,培养学生的主动探索、合作交流的能力和积极主动参与学习的精神。
四、教学重点和难点
教学重点:理解正方形与平行四边形、矩形、菱形之间的关系
教学难点:能熟练运用正方形的性质和判定进行有关的证明和计算.
教法分析
掌握正方形的概念是学好本节课的关键,通过动画演示,让学生认真观察图形变化,类比矩形、菱形的定义得出正方形的定义,通过问题引导,结合框架图和定义,理清正方形与菱形、矩形、平行四边形之间的关系,从而引导学生归纳出正方形的判定.利用图形进行比较教学,学生比较容易理解,同时很清楚各种图形之间的关系,发展学生系统归纳和逻辑思维能力。
六、学法分析
根据学法自由性原则,学生在教师创设的问题情景下,积极思考,自由参与知识的发生、发展、发现的过程,获取新的知识,体现了素质教育中学生学习能力的培养问题。在整个学习过程中,以“自主参与、勇于探索、合作交流”的探索式学法为主,加强学生自己会用类比方法学习,以达到教学的目的。
七、教学媒体与资源的选择与应用
1.在教学过程中,将制作好的课件在西沃白板上展示出来。2.让学生准备矩形纸片两张、小剪刀、三角板、菱形纸片一张。
八、教学过程
教学环节 教学过程
导入 1回顾思考对比平行四边形、矩形、菱形、正方形的性质 2、回顾思考对比平行四边形、矩形、菱形之间的判定关系 3、怎样判定一个四边形是正方形呢? 设计意图:通过问题串的设置,引发学生思考,潜移默化中构建正方形与平行四边形、菱形、矩形的联系,并引出课题
知识讲解 (难点突破) 探究正方形的判定 活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证. 猜想:满足怎样条件的矩形是正方形 请证明:对角线互相垂直的矩形是正方形. 已知:如图,在矩形ABCD中,对角线AC⊥DB. 求证:四边形ABCD是正方形. 活动2 把能活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形. 猜想 : 满足怎样条件的菱形是正方形? 请证明:对角线相等的菱形是正方形. 已知:如图,在菱形ABCD中,对角线AC=DB. 求证:四边形ABCD是正方形. 想一想:正方形判定有几条途径? 设计意图:调动学生已有的学习经验,结合正方形是特殊的矩形和特殊的菱形这一特性,使学生很自然的总结出正方形的判定.从“什么是正方形”,发展到“正方形是什么样的”,让学生自己总结出由菱形到正方形;由矩形到正方形;由平行四边形到正方形三条途径;实现思维方法上的延续与提升,让学生从正方形的性质中感悟做人的道理,提升学生的人为素养. 例题讲解 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形. 已知:如图,正方形ABCD中,对角线AC、BD相交于O. 求证:△ABO,△BCO,△CDO; △DAO是全等的等腰直角三角形 【设计意图】引导学生把几何命题符号化、具体化,进一步明确问题的条件和目标.教师强调书写格式的规范性、严谨性,体会转化思想在解决问题中的作用.
课堂练习 (难点巩固) 1.下列命题正确的是( ) A.四个角都相等的四边形是正方形 B.四条边都相等的四边形是正方形 C.对角线相等的平行四边形是正方形 D.对角线互相垂直的矩形是正方形 2.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A.当AB=BC时,四边形ABCD是菱形 B.当AC⊥BD时,四边形ABCD是菱形 C.当∠ABC=90°时,四边形ABCD是矩形 D.当AC=BD时,四边形ABCD是正方形 3.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件____________________,可得出该四边形是正方形. 4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________________(只填写序号). 5.如图,在四边形ABCD中, AB=BC ,对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD ,垂足分别为M、N. (1) 求证:∠ADB=∠CDB; (2) 若∠ADC=90 ,求证:四边形MPND是正方形. 6.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB. (1)试说明四边形AEDF的形状,并说明理由; (2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么? (3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由. 设计意图:设置由浅入深的分层练习,让学生对正方形的判定进行巩固。最后一题设置第一问平行四边形,第二问为判定菱形,第三问为正方形,切合主题。
小结 平行四边形、矩形、菱形、正方形之间判定的关系 平行四边形、矩形、菱形 、正方形之间的关系 本章学习了哪些四边形?是按照怎样的研究思路进行的? 平行四边形——矩形、菱形——正方形........,按由一般到特殊的思路研究的。 研究各种四边形时,我们的研究内容、研究步骤、研究方法各是怎样的? 研究内容:边、角、对角线的特征 研究步骤:下定义、探性质、研判定。 研究方法: (1)把四边形的问题转化为三角形。 (2)特殊平行四边形类比平行四边形研究。 设计意图:对本节课的知识点进行总结,使学生在头脑中的知识得到强化和提炼。
作业布置 课本p68面,T5、T6、T14 板书设计 1.正方形的判定方法 一组邻边相等的矩形是正方形; 有一个角是直角的菱形是正方形. 正方形性质和判定的应用 【设计意图】清晰明了的板书设计,突出本节课的教学重点,便于学生梳理、归纳正方形的知识框架.
九、教学反思
本节课的教学注意挖掘教材中培养创新意识的素材,在探索正方形判定方法的过程中,充分发挥了学生主体性,让学生经历自主“做数学”的过程---动手折纸,演示自制教具,并播放矩形、菱形、平行四边形的一个角、一组邻边的变化得到正方形课件,成功的达到了学生对正方形直观认识,进而探索出正方形的判定方法。为学生营造一种创新的学习氛围,把学生引上探索问题之路,成功的达到了让学生直观认识正方形的目的。给学生动手操作的机会,变被动为主动学习,引导通过感官的思维去观察、探究、分析知识形成的过程,以此深化知识、更深刻理解知识、主动获取知识,养成良好的学习习惯.
