第二单元《3的倍数的特征》 分课时教学设计2023-2024 五年级数学 下册 (人教版)
文档属性
| 名称 | 第二单元《3的倍数的特征》 分课时教学设计2023-2024 五年级数学 下册 (人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 18:53:28 | ||
图片预览




文档简介
第二单元《3的倍数的特征》 分课时教学设计
教学内容
人教版义务教育教科书五年级下册第二单元第10~11页内容。
教材分析
《3的倍数的特征》是人教版小学数学五年级下册《因数和倍数》中的内容。本单元的内容是在学生已经学了一定的整数知识(整数的认识、整数的四则运算及应用)的基础上,进一步认识整数的性质,本单元的知识作为数论知识的初步,一直是小学数学教材中的重要内容。本课时的教学是在学生了解了因数与倍数的相关概念的基础上,从找一个数的倍数出发,掌握了2和5的倍数的特征后,进一步研究特殊数的倍数的特征的学习过程。2、5的倍数的特征体现在个位上,而3的倍数的特征,只看个位数来判定恰恰成了“陷阱”,怎样让学生想到转换思路,从只看个位到“求和”?教材通过学生对话插图,在学生思维的转折处引导学生观察、操作、推理、发现、归纳。重在培养学生的数感、运算能力、推理意识、应用意识和创新意识。
学情分析
学生学习了2、5倍数的特征,容易形成思维惯性,认为通过观察一个数的个位数就能发现3的倍数的特征,但这一活动经验恰恰是判定3的倍数特征的“陷阱”,打破思维定式,另辟蹊径,让思路及时转向对学生来说有一定的难度。让学生体验到探究式学习过程中“山穷水尽”的无力感与“柳暗花明”的成功喜悦感更有一定的难度。
设计思路
基于教材,基于儿童,在设计本课教学时我以“听音辨数”游戏激戏引入,让学生在观察——猜想——推翻猜想——再观察——再猜想——验证的过程中,概括出3的倍数的特征。
方法与策略
由于3的倍数的特征与2、5倍数的特征有很大的不同,如果教学时让学生依次算出3的倍数,再直截了当的提示:“把各位上的数相加,你发现了什么?”虽说效果明显,但问题过于直白,不利于学生获得探究的体验。基与以上思考,教学时让学生先在已有经验的基础上去猜想并质疑,再借助百数表推翻猜想,然后在计数器拨珠的过程重新猜想,借助百数表验证猜想,利用图形分割证明猜想,这一过程让学生亲历了探究式学习的全过程,更利于培养学生的数学核心素养。
教学目标
1.经历探索3的倍数的特征的过程,掌握3的倍数的特征,能依据3的倍数的特征判断一个数是否是3的倍数。
2.积累观察、猜想、归纳等思维活动经验,培养学生的数感,运算能力、合情推理的能力,发展学生的应用意识和创新意识。
3.在探索活动的过程中能主动与他人合作交流,感受数学学习的乐趣,感悟数学思维的严谨性。
教学重点:探索并掌握3的倍数的特征。
教学难点:理解3的倍数的特征,了解3的倍数特征的原理。
教学准备:多媒体课件、学习任务单
教学过程:
一、激趣引入
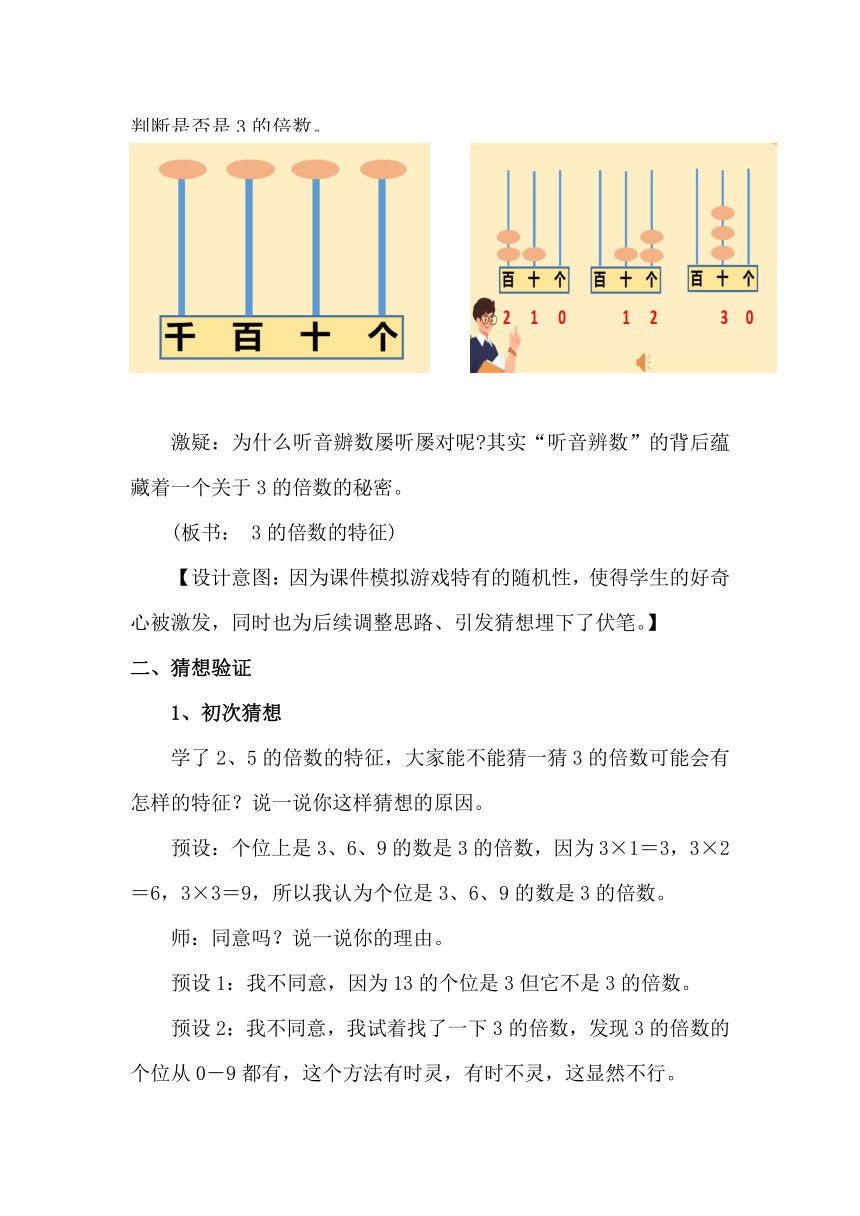
小游戏:学生拨珠(此处课件出示随机拨珠计数器),教师听音判断是否是3的倍数。
激疑:为什么听音辦数屡听屡对呢 其实“听音辨数”的背后蕴藏着一个关于3的倍数的秘密。
(板书: 3的倍数的特征)
【设计意图:因为课件模拟游戏特有的随机性,使得学生的好奇心被激发,同时也为后续调整思路、引发猜想埋下了伏笔。】
二、猜想验证
1、初次猜想
学了2、5的倍数的特征,大家能不能猜一猜3的倍数可能会有怎样的特征?说一说你这样猜想的原因。
预设:个位上是3、6、9的数是3的倍数,因为3×1=3,3×2=6,3×3=9,所以我认为个位是3、6、9的数是3的倍数。
师:同意吗?说一说你的理由。
预设1:我不同意,因为13的个位是3但它不是3的倍数。
预设2:我不同意,我试着找了一下3的倍数,发现3的倍数的个位从0-9都有,这个方法有时灵,有时不灵,这显然不行。
2、初次验证
师:到底是猜想更接近真相,还是我们的质疑更有道理,我们还需要验证。
(1)提出要求:请出老朋友“百数表”(课件出示百数表),圈出3的倍数,看看我们的猜想能否成立。
(2)学生活动。
(3)汇报结果
(4)小结:只要一个反例,就足以把猜想推翻。看来,判断一个数是不是3的倍数,只看个位是行不通的,需要换一个思路重新出发。
【设计意图:受2、5倍数的影响,学生极可能在类比猜想时产生的负迁移,教师以学定教,运用课件顺势而导,让学生经历类比推理可能无效的真实体验。培养学生的探索意识。】
3、再次猜想
(1)启发思路: “听音辨数”时(课件重温“听音辨数”),老师的判断又对又快,我们重温一下。在拨珠的过程中提问:老师有可能是根据什么来判断的呢
根据学生的回答,师板书:所用珠子的个数。
(2)再次猜想:到底怎样的数就一定是3的倍数呢?现在,你会有什么猜想
生:是3的倍数的数,所用珠子的个数也是3的倍数。
【设计意图:与“2、5的倍数的特征”相比,“3的倍数的特征”比较隐蔽,学生不容易发现。相比而言,课件中电子计数器的出现为学生提出了研究的方向,也更利于学生提出猜想,并验证猜想,从而发现规律。】
4、再次验证
(1)提出要求:
在百数表中任意找几个数,并在计数器上拨一拨(课件同步),然后在学习单上算出各用了几颗珠子,最后比对验证结果与猜想是否一致。
(2)学生活动
(3)学生汇报
预设1:我观察的是60、24、15……,在计数器上拨数时各用了6颗珠子,珠子总数是3的倍数,它们也是3的倍数。
预设2:我观察的是13、26、39,拨13、26时所用珠子的个数不是3的倍数,它们也不是3的倍数,拨39时用了12颗珠子,珠子总数是3的倍数,39也是3的倍数。
(4)小结:猜想结果正确。
【设计意图:“猜想—验证”是探究发现的重要方法。在举例验证猜想时采用小组合作探究的形式,让学生借助课件展示全面研究了“所选数是不是3的倍数”和“所用珠子的个数”之间的关系,在归纳推理中初步得出结论,培养了学生思维的严谨性和缜密性。】
三、得出结论
1、根据刚才的经验判断计数器上的312和153是不是3的倍数。
2、没有计数器作参考的数,怎样判断它是不是3的倍数?
根据学生的回答得到3的倍数的特征:3的倍数的数,各位上数的和是3的倍数。
【设计意图:从借助计数器看“珠子的个数”进行判断,到“没有珠、只有数”的直接判断,凸显了从“珠”到“数”的抽象,使推理有根有据。揭示“百数表”的秘密是本节课教学的小亮点,让学生更加清楚地看到了3的倍数的分布排列,从抽象回到具体,强化了学生对3的倍数的特征的认识。】
四、解释说理
提出问题:为什么2或5的倍数时只要看个位,而判断是不是3的倍数时,却要看各位上数的和呢?
1、结合课件演示,解释2、5的倍数要看个位的原理。
2、以42、422为例,结合刚才的经验,让学生在图上圈一圈,找一找3的倍数特征的原理。
五、应用提升
1、倍数消消乐——消除3的倍数比赛
2、狐狸爸爸每月工资为856元,他3个月的工资是多少?
狐狸爸爸认为:856×3=2468(元);
狐狸妈妈认为:856×3=2558(元);
小狐狸认为:856×3=2568(元)。
请你用今天学习的办法,快速地判断谁可能是正确的。
分别在方框里填上一个数字,使这个数是3 的倍数。
【设计意图:两个游戏的设计,两种不同层次的练习,不但让学生巩固了今天所学新知,同时也在新知中找到捷径。让学生体会到成果的喜悦。】
六、回顾反思
回顾一下这节课我们研究了什么?你有哪些收获呢 我们又是怎样一步步探究得出3的倍数的特征的呢
带着这些经验,你还能研究其它数的特征吗?
【设计意图:本节课的回顾反思力求让学生领悟探究这类数学问题的一般过程与基本方法,多媒体课件的运用促进了结构化的建构,引发学生自觉向课外延伸和拓展。】
练习设计
1、圈出3的倍数
92 75 36 206 65 3051 779 9999
111 49 165 5988 655 131 2222 72031
2、在 里填一个数,使组成的数是3的倍数, 里可以填几?
□7 4□2 □44 26□ □12
3、既是2的倍数,又是3的倍数的最大两位数是 ,既有因数5又有因数3的最小三位数是 。
4、学习商店每个笔记本6元,每只钢笔18元,王老师卖了一些笔记本和钢笔给了售货员100元,找回2元,对吗?为什么?
教学反思
如何让学生体验到探究式学习过程中“山水水尽”的无力感与“柳暗花明”的成功喜悦感?基于课标、基于教材、基于儿童我是这样设计并教学本课时的。
一、激趣引入。我以“听音辨数”游戏激戏引入——学生拨珠,教师听音判断是否是3的倍数。从“看数”判断一个数是否是2、5的倍数,到时“听数”就能判断一个数是否是3的倍数,由于游戏具有的随机性及从“看”到“听”判断方法的变换,使得学生的好奇心被激发,同时也为后续调整思路、引发猜想埋下了伏笔。
二、初次猜想。在游戏过程中老师为什么能够判断得又对又快?学生认为老师一定是掌握了3的倍数的特征,在此基础上我及时引发学生猜想——请大家猜一猜3的倍数有什么特征?大部分同学认为“个位是3、6、9的数一定是3的倍数”,也有部分同学对此猜想提出了质疑。到底是猜想更接近真相还是质疑更有道理?
三、初次验证。此时、及时请出“老朋友”百数表,组织学生开展数学活动“圈出百数表中3的倍数”,学生通过活动发现13、26、49这些数的个位是3、6、9但它们不是3的倍数。我及时小结“举一个反例就可以推翻猜想”,教给了学生探究过程中排除干扰的方法,再引导学生进一步观察圈起来的数的个位发现从0到9都有,显然,判断一个数是否是3的倍数,只看个位是行不通的,从而启发学生“另辟蹊径”换一个思路重新出发。受2、5倍数的影响,学生极可能在类比猜想时产生负迁移,我以学定教,顺势而导,让学历经类比推理可能无效的真实体验,培养了学生的探究意识。
四、再次猜想。那么3的倍数的特征到底隐藏在哪呢?我启发思路,重温“听音辨数”,在拨珠的过程中提问:老师有可能是根据什么来判断的呢?学生发现是根据所有珠子的个数来发现的。此时,让学生再次猜想3的倍数的特征。与“2、5的倍数的特征”相比,“3的倍数的特征”比较隐蔽,学生不容易发现。相比而言,计数器的出现为学生提出了研究的方向,也更利于学生提出猜想,并验证猜想。
教学内容
人教版义务教育教科书五年级下册第二单元第10~11页内容。
教材分析
《3的倍数的特征》是人教版小学数学五年级下册《因数和倍数》中的内容。本单元的内容是在学生已经学了一定的整数知识(整数的认识、整数的四则运算及应用)的基础上,进一步认识整数的性质,本单元的知识作为数论知识的初步,一直是小学数学教材中的重要内容。本课时的教学是在学生了解了因数与倍数的相关概念的基础上,从找一个数的倍数出发,掌握了2和5的倍数的特征后,进一步研究特殊数的倍数的特征的学习过程。2、5的倍数的特征体现在个位上,而3的倍数的特征,只看个位数来判定恰恰成了“陷阱”,怎样让学生想到转换思路,从只看个位到“求和”?教材通过学生对话插图,在学生思维的转折处引导学生观察、操作、推理、发现、归纳。重在培养学生的数感、运算能力、推理意识、应用意识和创新意识。
学情分析
学生学习了2、5倍数的特征,容易形成思维惯性,认为通过观察一个数的个位数就能发现3的倍数的特征,但这一活动经验恰恰是判定3的倍数特征的“陷阱”,打破思维定式,另辟蹊径,让思路及时转向对学生来说有一定的难度。让学生体验到探究式学习过程中“山穷水尽”的无力感与“柳暗花明”的成功喜悦感更有一定的难度。
设计思路
基于教材,基于儿童,在设计本课教学时我以“听音辨数”游戏激戏引入,让学生在观察——猜想——推翻猜想——再观察——再猜想——验证的过程中,概括出3的倍数的特征。
方法与策略
由于3的倍数的特征与2、5倍数的特征有很大的不同,如果教学时让学生依次算出3的倍数,再直截了当的提示:“把各位上的数相加,你发现了什么?”虽说效果明显,但问题过于直白,不利于学生获得探究的体验。基与以上思考,教学时让学生先在已有经验的基础上去猜想并质疑,再借助百数表推翻猜想,然后在计数器拨珠的过程重新猜想,借助百数表验证猜想,利用图形分割证明猜想,这一过程让学生亲历了探究式学习的全过程,更利于培养学生的数学核心素养。
教学目标
1.经历探索3的倍数的特征的过程,掌握3的倍数的特征,能依据3的倍数的特征判断一个数是否是3的倍数。
2.积累观察、猜想、归纳等思维活动经验,培养学生的数感,运算能力、合情推理的能力,发展学生的应用意识和创新意识。
3.在探索活动的过程中能主动与他人合作交流,感受数学学习的乐趣,感悟数学思维的严谨性。
教学重点:探索并掌握3的倍数的特征。
教学难点:理解3的倍数的特征,了解3的倍数特征的原理。
教学准备:多媒体课件、学习任务单
教学过程:
一、激趣引入
小游戏:学生拨珠(此处课件出示随机拨珠计数器),教师听音判断是否是3的倍数。
激疑:为什么听音辦数屡听屡对呢 其实“听音辨数”的背后蕴藏着一个关于3的倍数的秘密。
(板书: 3的倍数的特征)
【设计意图:因为课件模拟游戏特有的随机性,使得学生的好奇心被激发,同时也为后续调整思路、引发猜想埋下了伏笔。】
二、猜想验证
1、初次猜想
学了2、5的倍数的特征,大家能不能猜一猜3的倍数可能会有怎样的特征?说一说你这样猜想的原因。
预设:个位上是3、6、9的数是3的倍数,因为3×1=3,3×2=6,3×3=9,所以我认为个位是3、6、9的数是3的倍数。
师:同意吗?说一说你的理由。
预设1:我不同意,因为13的个位是3但它不是3的倍数。
预设2:我不同意,我试着找了一下3的倍数,发现3的倍数的个位从0-9都有,这个方法有时灵,有时不灵,这显然不行。
2、初次验证
师:到底是猜想更接近真相,还是我们的质疑更有道理,我们还需要验证。
(1)提出要求:请出老朋友“百数表”(课件出示百数表),圈出3的倍数,看看我们的猜想能否成立。
(2)学生活动。
(3)汇报结果
(4)小结:只要一个反例,就足以把猜想推翻。看来,判断一个数是不是3的倍数,只看个位是行不通的,需要换一个思路重新出发。
【设计意图:受2、5倍数的影响,学生极可能在类比猜想时产生的负迁移,教师以学定教,运用课件顺势而导,让学生经历类比推理可能无效的真实体验。培养学生的探索意识。】
3、再次猜想
(1)启发思路: “听音辨数”时(课件重温“听音辨数”),老师的判断又对又快,我们重温一下。在拨珠的过程中提问:老师有可能是根据什么来判断的呢
根据学生的回答,师板书:所用珠子的个数。
(2)再次猜想:到底怎样的数就一定是3的倍数呢?现在,你会有什么猜想
生:是3的倍数的数,所用珠子的个数也是3的倍数。
【设计意图:与“2、5的倍数的特征”相比,“3的倍数的特征”比较隐蔽,学生不容易发现。相比而言,课件中电子计数器的出现为学生提出了研究的方向,也更利于学生提出猜想,并验证猜想,从而发现规律。】
4、再次验证
(1)提出要求:
在百数表中任意找几个数,并在计数器上拨一拨(课件同步),然后在学习单上算出各用了几颗珠子,最后比对验证结果与猜想是否一致。
(2)学生活动
(3)学生汇报
预设1:我观察的是60、24、15……,在计数器上拨数时各用了6颗珠子,珠子总数是3的倍数,它们也是3的倍数。
预设2:我观察的是13、26、39,拨13、26时所用珠子的个数不是3的倍数,它们也不是3的倍数,拨39时用了12颗珠子,珠子总数是3的倍数,39也是3的倍数。
(4)小结:猜想结果正确。
【设计意图:“猜想—验证”是探究发现的重要方法。在举例验证猜想时采用小组合作探究的形式,让学生借助课件展示全面研究了“所选数是不是3的倍数”和“所用珠子的个数”之间的关系,在归纳推理中初步得出结论,培养了学生思维的严谨性和缜密性。】
三、得出结论
1、根据刚才的经验判断计数器上的312和153是不是3的倍数。
2、没有计数器作参考的数,怎样判断它是不是3的倍数?
根据学生的回答得到3的倍数的特征:3的倍数的数,各位上数的和是3的倍数。
【设计意图:从借助计数器看“珠子的个数”进行判断,到“没有珠、只有数”的直接判断,凸显了从“珠”到“数”的抽象,使推理有根有据。揭示“百数表”的秘密是本节课教学的小亮点,让学生更加清楚地看到了3的倍数的分布排列,从抽象回到具体,强化了学生对3的倍数的特征的认识。】
四、解释说理
提出问题:为什么2或5的倍数时只要看个位,而判断是不是3的倍数时,却要看各位上数的和呢?
1、结合课件演示,解释2、5的倍数要看个位的原理。
2、以42、422为例,结合刚才的经验,让学生在图上圈一圈,找一找3的倍数特征的原理。
五、应用提升
1、倍数消消乐——消除3的倍数比赛
2、狐狸爸爸每月工资为856元,他3个月的工资是多少?
狐狸爸爸认为:856×3=2468(元);
狐狸妈妈认为:856×3=2558(元);
小狐狸认为:856×3=2568(元)。
请你用今天学习的办法,快速地判断谁可能是正确的。
分别在方框里填上一个数字,使这个数是3 的倍数。
【设计意图:两个游戏的设计,两种不同层次的练习,不但让学生巩固了今天所学新知,同时也在新知中找到捷径。让学生体会到成果的喜悦。】
六、回顾反思
回顾一下这节课我们研究了什么?你有哪些收获呢 我们又是怎样一步步探究得出3的倍数的特征的呢
带着这些经验,你还能研究其它数的特征吗?
【设计意图:本节课的回顾反思力求让学生领悟探究这类数学问题的一般过程与基本方法,多媒体课件的运用促进了结构化的建构,引发学生自觉向课外延伸和拓展。】
练习设计
1、圈出3的倍数
92 75 36 206 65 3051 779 9999
111 49 165 5988 655 131 2222 72031
2、在 里填一个数,使组成的数是3的倍数, 里可以填几?
□7 4□2 □44 26□ □12
3、既是2的倍数,又是3的倍数的最大两位数是 ,既有因数5又有因数3的最小三位数是 。
4、学习商店每个笔记本6元,每只钢笔18元,王老师卖了一些笔记本和钢笔给了售货员100元,找回2元,对吗?为什么?
教学反思
如何让学生体验到探究式学习过程中“山水水尽”的无力感与“柳暗花明”的成功喜悦感?基于课标、基于教材、基于儿童我是这样设计并教学本课时的。
一、激趣引入。我以“听音辨数”游戏激戏引入——学生拨珠,教师听音判断是否是3的倍数。从“看数”判断一个数是否是2、5的倍数,到时“听数”就能判断一个数是否是3的倍数,由于游戏具有的随机性及从“看”到“听”判断方法的变换,使得学生的好奇心被激发,同时也为后续调整思路、引发猜想埋下了伏笔。
二、初次猜想。在游戏过程中老师为什么能够判断得又对又快?学生认为老师一定是掌握了3的倍数的特征,在此基础上我及时引发学生猜想——请大家猜一猜3的倍数有什么特征?大部分同学认为“个位是3、6、9的数一定是3的倍数”,也有部分同学对此猜想提出了质疑。到底是猜想更接近真相还是质疑更有道理?
三、初次验证。此时、及时请出“老朋友”百数表,组织学生开展数学活动“圈出百数表中3的倍数”,学生通过活动发现13、26、49这些数的个位是3、6、9但它们不是3的倍数。我及时小结“举一个反例就可以推翻猜想”,教给了学生探究过程中排除干扰的方法,再引导学生进一步观察圈起来的数的个位发现从0到9都有,显然,判断一个数是否是3的倍数,只看个位是行不通的,从而启发学生“另辟蹊径”换一个思路重新出发。受2、5倍数的影响,学生极可能在类比猜想时产生负迁移,我以学定教,顺势而导,让学历经类比推理可能无效的真实体验,培养了学生的探究意识。
四、再次猜想。那么3的倍数的特征到底隐藏在哪呢?我启发思路,重温“听音辨数”,在拨珠的过程中提问:老师有可能是根据什么来判断的呢?学生发现是根据所有珠子的个数来发现的。此时,让学生再次猜想3的倍数的特征。与“2、5的倍数的特征”相比,“3的倍数的特征”比较隐蔽,学生不容易发现。相比而言,计数器的出现为学生提出了研究的方向,也更利于学生提出猜想,并验证猜想。
