人教版六年级数学下册第4课时 立体图形的认识与测量课件(共18张PPT)
文档属性
| 名称 | 人教版六年级数学下册第4课时 立体图形的认识与测量课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 20:04:45 | ||
图片预览



文档简介
(共18张PPT)
六年级下册
立体图形的认识与测量(2)
复习导入
立体图形的表面积指的是什么?
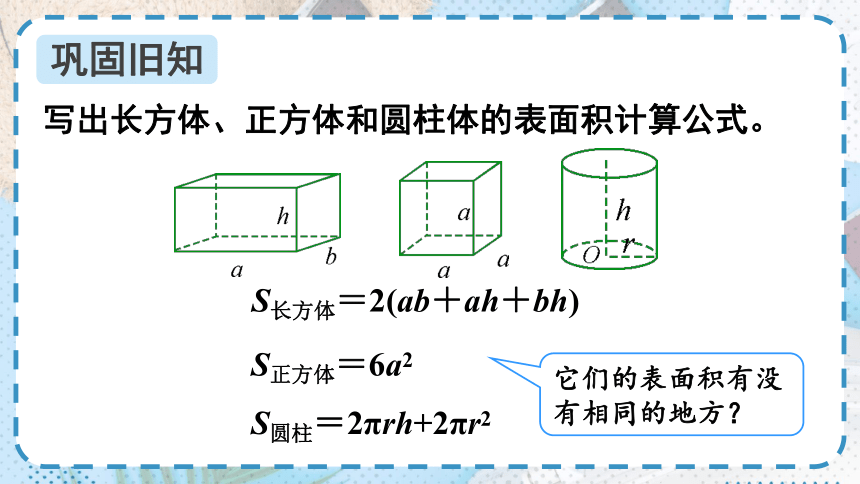
写出长方体、正方体和圆柱体的表面积计算公式。
S长方体=2(ab+ah+bh)
S正方体=6a2
S圆柱=2πrh+2πr2
巩固旧知
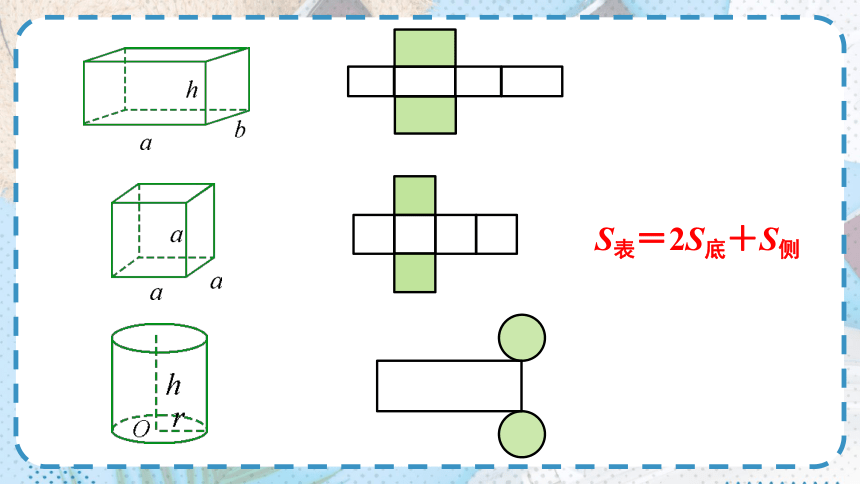
它们的表面积有没有相同的地方?
S表=2S底+S侧
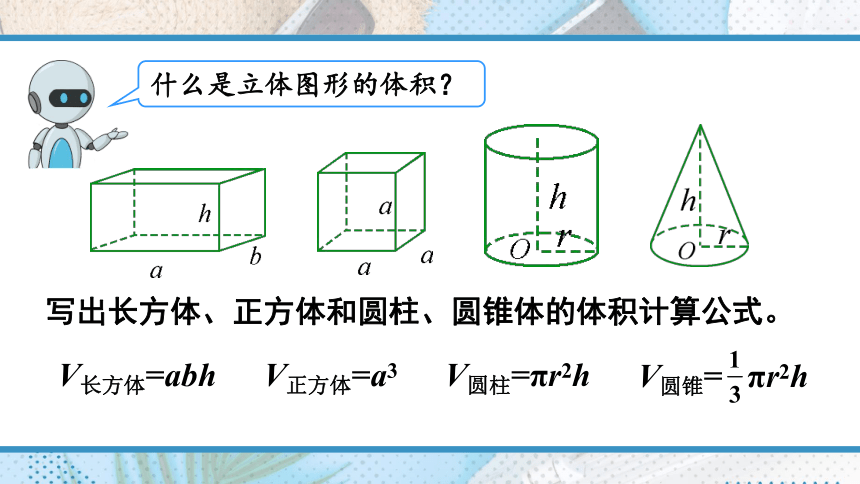
什么是立体图形的体积?
写出长方体、正方体和圆柱、圆锥体的体积计算公式。
V长方体=abh
V正方体=a3
V圆柱=πr2h
V圆锥= πr2h
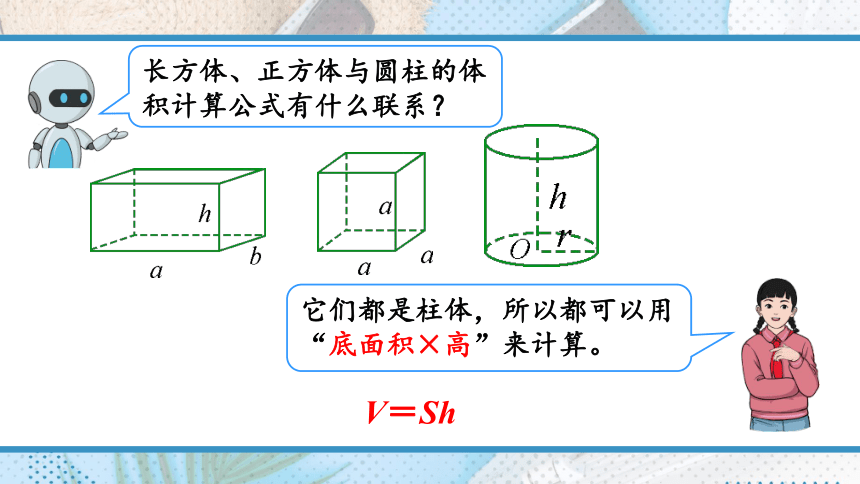
长方体、正方体与圆柱的体积计算公式有什么联系?
它们都是柱体,所以都可以用“底面积×高”来计算。
V=Sh
当物体作为容器时就需要计算容积,体积和容积有什么区别和联系?
体积和容积采用的计算方法相同,不同的是体积计算数据是从物体外面量得的,容积计算数据需要从里面量。
立体图形 表面积计算公式 体积计算公式
S=2(ab+ah+bh)
S=6a2
S=2πrh+2πr2
V=abh
V=a3
V=πr2h
V= πr2h
V=Sh
1.怎样测量出一块拳头大的鹅卵石的体积?
不规则物体体积 规则物体体积
转化
随堂练习
【教材P87 做一做 第1题】
在量杯中装一些水,并把鹅卵石浸没水中(水未溢出),读出放入鹅卵石前后量杯中水面的刻度,算出差,就是鹅卵石的体积。
2. 把下面这个展开图折成一个长方体(字母在长方体的内侧)。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
F
E
【教材P89 练习十八 第9题】
2. 把下面这个展开图折成一个长方体(字母在长方体的内侧)。
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
【教材P89 练习十八 第9题】
量出B面的长和宽,E面的宽。(合理即可)
3. 把一个棱长为6cm的正方体切成棱长为2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
【教材P89 练习十八 第10题】
大正方体的体积:6×6×6=216(cm3)
小正方体的体积:2×2×2=8(cm3)
216÷8=27(个)
大正方体的表面积:6×6×6=216(cm2)
小正方体的表面积:2×2×6×27=648(cm2)
648 – 216=432(cm2)
答:可以得到27个小正方体,它们的表面积之和比原来大正方体的表面积增加了432cm2。
4. 把一个棱长为10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留一位小数。)
10×10×10÷[ ×3.14×(20÷2)2]≈9.6(cm)
1
3
答:这个圆锥形铁块的高约是9.6cm。
【教材P90 练习十八 第11题】
5. 一个箱子下半部的形状是棱长为20cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
表面积:
20×20×5+3.14×20×20÷2+3.14×(20÷2)2
=2942(cm2)
体积:20×20×20+3.14×102×20÷2=11140(cm3)
【教材P90 练习十八 第13题】
6.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10÷4=7.85(cm2)
答:涂色部分的面积是7.85cm2。
【教材P90 练习十八 第15*题】
6.用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
当围成正方体时,用纸最多。
24÷12=2(cm) 2×2×6=24(cm2)
【教材P90 练习十八 第16*题】
课堂小结
S表=2S底+S侧
S长方体=2(ab+ah+bh)
S正方体=6a2
S圆柱=2πrh+2πr2
V=Sh
V长方体=abh
V正方体=a3
V圆柱=πr2h
V圆锥= πr2h
六年级下册
立体图形的认识与测量(2)
复习导入
立体图形的表面积指的是什么?
写出长方体、正方体和圆柱体的表面积计算公式。
S长方体=2(ab+ah+bh)
S正方体=6a2
S圆柱=2πrh+2πr2
巩固旧知
它们的表面积有没有相同的地方?
S表=2S底+S侧
什么是立体图形的体积?
写出长方体、正方体和圆柱、圆锥体的体积计算公式。
V长方体=abh
V正方体=a3
V圆柱=πr2h
V圆锥= πr2h
长方体、正方体与圆柱的体积计算公式有什么联系?
它们都是柱体,所以都可以用“底面积×高”来计算。
V=Sh
当物体作为容器时就需要计算容积,体积和容积有什么区别和联系?
体积和容积采用的计算方法相同,不同的是体积计算数据是从物体外面量得的,容积计算数据需要从里面量。
立体图形 表面积计算公式 体积计算公式
S=2(ab+ah+bh)
S=6a2
S=2πrh+2πr2
V=abh
V=a3
V=πr2h
V= πr2h
V=Sh
1.怎样测量出一块拳头大的鹅卵石的体积?
不规则物体体积 规则物体体积
转化
随堂练习
【教材P87 做一做 第1题】
在量杯中装一些水,并把鹅卵石浸没水中(水未溢出),读出放入鹅卵石前后量杯中水面的刻度,算出差,就是鹅卵石的体积。
2. 把下面这个展开图折成一个长方体(字母在长方体的内侧)。
(1)如果A面在底部,那么哪一面在上面?
(2)如果F面在前面,从左面看是B面,那么哪一面在上面?
F
E
【教材P89 练习十八 第9题】
2. 把下面这个展开图折成一个长方体(字母在长方体的内侧)。
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度?
【教材P89 练习十八 第9题】
量出B面的长和宽,E面的宽。(合理即可)
3. 把一个棱长为6cm的正方体切成棱长为2cm的小正方体,可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
【教材P89 练习十八 第10题】
大正方体的体积:6×6×6=216(cm3)
小正方体的体积:2×2×2=8(cm3)
216÷8=27(个)
大正方体的表面积:6×6×6=216(cm2)
小正方体的表面积:2×2×6×27=648(cm2)
648 – 216=432(cm2)
答:可以得到27个小正方体,它们的表面积之和比原来大正方体的表面积增加了432cm2。
4. 把一个棱长为10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留一位小数。)
10×10×10÷[ ×3.14×(20÷2)2]≈9.6(cm)
1
3
答:这个圆锥形铁块的高约是9.6cm。
【教材P90 练习十八 第11题】
5. 一个箱子下半部的形状是棱长为20cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
表面积:
20×20×5+3.14×20×20÷2+3.14×(20÷2)2
=2942(cm2)
体积:20×20×20+3.14×102×20÷2=11140(cm3)
【教材P90 练习十八 第13题】
6.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm2,涂色部分的面积是多少?
3.14×10÷4=7.85(cm2)
答:涂色部分的面积是7.85cm2。
【教材P90 练习十八 第15*题】
6.用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多?
当围成正方体时,用纸最多。
24÷12=2(cm) 2×2×6=24(cm2)
【教材P90 练习十八 第16*题】
课堂小结
S表=2S底+S侧
S长方体=2(ab+ah+bh)
S正方体=6a2
S圆柱=2πrh+2πr2
V=Sh
V长方体=abh
V正方体=a3
V圆柱=πr2h
V圆锥= πr2h
