26.3.1 探索生活中的抛物线形问题习题课件(30张PPT)2023-2024学年华东师大版数学九年级下册
文档属性
| 名称 | 26.3.1 探索生活中的抛物线形问题习题课件(30张PPT)2023-2024学年华东师大版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 21:11:25 | ||
图片预览










文档简介
(共30张PPT)
26.3 实践与探索
课时1 探索生活中的抛物线形问题
过基础 教材必备知识精练
1.[2023宜昌中考]如图,一名学生推铅球,铅球
行进高度 (单位: )与水平距离 (单
位: )之间的关系是
,则铅球推出的距离
____ .
10
【解析】 令 ,则 ,解得 ,
, .
2.[2023滨州中考]如图,要修一个圆形喷水池,在
池中心竖直安装一根水管,水管的顶端安一个喷水
头,使喷出的抛物线形水柱在与池中心的水平距离
为 处达到最高,高度为 ,水柱落地处离池
中心 ,水管长度应为_______.
2.25m
【解析】 以池的中心为原点,竖直安装的水管为 轴,与水管垂直的水
平线为 轴建立平面直角坐标系.因为在距池中心的水平距离为 处达
到最高,高度为 ,所以设抛物线的表达式为
(顶点式),将 代入,得 ,
所以该抛物线的表达式为 .令 ,则
,故水管长度为 .
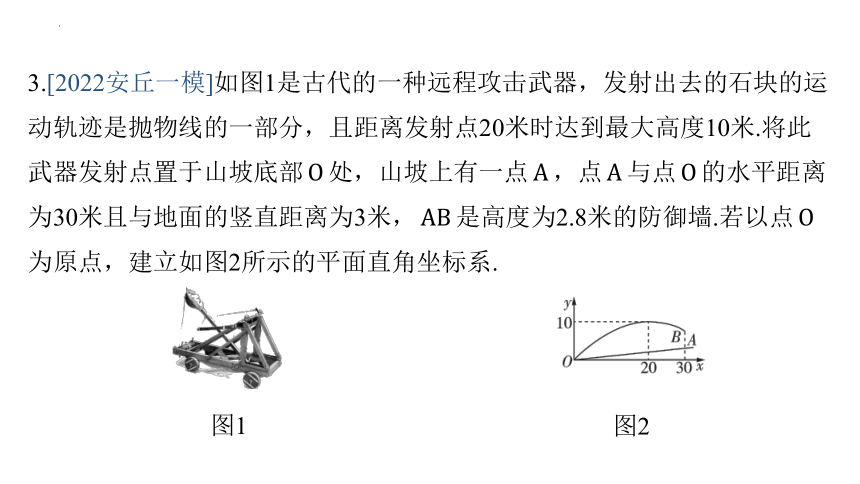
3.[2022安丘一模]如图1是古代的一种远程攻击武器,发射出去的石块的运
动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将此
武器发射点置于山坡底部 处,山坡上有一点 ,点 与点 的水平距离
为30米且与地面的竖直距离为3米, 是高度为2.8米的防御墙.若以点
为原点,建立如图2所示的平面直角坐标系.
图1
图2
(1)石块运动轨迹所在抛物线的表达式为_ ________________;
;
【解析】 设石块的运动轨迹所在抛物线的表达式为 ,
把 代入,得 ,解得 ,
,即 .
(2)石块____飞越防御墙 (填“能”或“不能”).
能
【解析】 把 代入 ,得 ,
, 石块能飞越防御墙 .
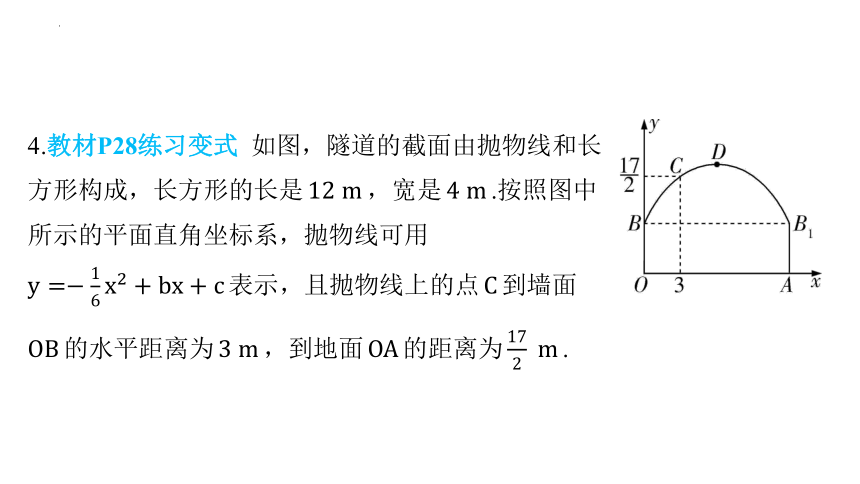
4.教材P28练习变式 如图,隧道的截面由抛物线和长
方形构成,长方形的长是 ,宽是 .按照图中
所示的平面直角坐标系,抛物线可用
表示,且抛物线上的点 到墙面
的水平距离为 ,到地面 的距离为 .
(1)求该抛物线对应的二次函数的表达式,并计算出拱顶 到地面
的距离.
解:由题意得点 的坐标为 ,点 的坐标为 ,
, 两点在抛物线 上,
解得
该抛物线对应的二次函数的表达式为 .
,
拱顶 到地面 的距离为 .
(2)一辆货运汽车载一长方体集装箱后高为 ,宽为 ,如果隧道
内设双向行车道,那么这辆货车能否安全通过?
由题意得这辆货车最外侧与地面 的交点为 或 ,
当 或 时, , ,
这辆货车能安全通过.
【解题通法】
判断汽车能否从隧道下通过
(1)固定汽车的宽,判断隧道是否够高(即已知 的值,根据函数
表达式求出 的值,比较限制的高与 值的大小);(2)固定汽车的高,
判断隧道是否够宽(即已知 的值,根据函数表达式求出 的值,比较限
制的宽与 值的大小).
26.3 实践与探索
课时1 探索生活中的抛物线形问题
过能力 学科关键能力构建
1.[2022黄冈三模]如图1,“东方之门”通过简单的几何曲线处理,将传统文
化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图2,“门”
的内侧曲线呈抛物线形,已知其底部宽度为 ,高度为 ,则离
地面 处的水平宽度(即 的长)为( )
图1
图2
C
A. B. C. D.
【解析】 如图,建立平面直角坐标系,易得 ,
, .设抛物线的表达式为
,将 代入,得
,解得 , 抛物线的表
达式为 .将 代入,得
,解得 , , ,
.
2.教材P34复习题 变式 株洲五桥主桥主孔为拱梁钢构组合体系,如图
1.小明在五桥观光,发现拱梁的路面部分有均匀排列着的9根支柱,他回
家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)为10米,于是
他建立了如图2所示的平面直角坐标系,将余下的8根支柱的高度都算出来
了,你认为中柱右边第二根支柱的高度是( )
图1
图2
D
A.7米 B.7.6米 C.8米 D.8.4米
【解析】 根据题意可得点 的坐标是 ,设抛物线对应的二次函数的表达式为 ,将点 的坐标代入 ,得 ,解得 ,所以该抛物线对应的函数表达式为
. 可设中柱右边第二根支柱上端点的坐标为 ,于是
,所以中柱右边第二根支柱的高度是 (米).
3.新情境[2023长春中考]2023年5月28日, 商业首航完成——中国民
航商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过
隆重的“水门礼”(寓意“接风洗尘”,是国际民航中高级别的礼仪).如图1,
在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水
柱近似看作形状相同的抛物线的一部分.如图2,当两辆消防车喷水口 ,
的水平距离为80米时,两条水柱在抛物线的顶点 处相遇,此时相遇
点 距地面20米,喷水口 , 距地面均为4米.若两辆消防车同时后退10
米,两条水柱的形状及喷水口 , 到地面的距离均保持不变,则此时
两条水柱相遇点 距地面____米.
19
图1
图2
【解析】 由题意可知, , , .设抛物线的表达
式为 ,将点 的坐标代入 ,解得
, 消防车同时后退10米, 抛物线
向左(右)平移10米,平移后抛物线的表达式为
,令 ,解得 .
素养提升
4.新考法 应用意识[2023贵州中考]如图1,是一座抛物线形拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图2),抛物线的顶点在 处,对称轴 与水平线 垂直, ,点 在抛物线上,且点 到对称轴的距离 ,点 在抛物线上,点 到对称轴的距离是1.
图1
图2
备用图
(1)求该抛物线的表达式;
解:设抛物线的表达式为 ,
把点 的坐标代入,得 ,解得 ,
该抛物线的表达式为 .
(2)如图2,为更加稳固,小星想在 上找一点 ,加装拉杆 , ,
同时使拉杆的长度之和最短,请你帮小星找到点 的位置并求出坐标;
【解析】 解题思路:作点 关于 轴的对称点 ,连接 交 于点 , 则点 即所求;
如图,作点 关于 轴的对称点 ,则 ,连接 交 于点 ,则点 即所求.
把 代入 ,得 ,
.
设直线 的表达式为 ,
解得 .
令 ,得 , 点 的坐标为 .
(3)为了造型更加美观,小星重新设计抛物线,其表达式为
,当 时,函数 的值总大于等于
9.求 的取值范围.
【解析】 解题思路:分 , ,
三种情况讨论,结合二次函数的图象和性质,列不等式求得
的取值范围.
,
抛物线的对称轴为直线 ,顶点坐标为 .
①当 时,得 ,
解得 , .
②当 时,由 ,得 ,
(抛物线开口向下,点离对称轴的距离越远,对应的函数值越小),解得 , .
由 ,得 ,
,解得 , .
故当 时,都成立.
③当 时,得 ,
解得 , .
综上所述, 的取值范围为 .
26.3 实践与探索
课时1 探索生活中的抛物线形问题
过基础 教材必备知识精练
1.[2023宜昌中考]如图,一名学生推铅球,铅球
行进高度 (单位: )与水平距离 (单
位: )之间的关系是
,则铅球推出的距离
____ .
10
【解析】 令 ,则 ,解得 ,
, .
2.[2023滨州中考]如图,要修一个圆形喷水池,在
池中心竖直安装一根水管,水管的顶端安一个喷水
头,使喷出的抛物线形水柱在与池中心的水平距离
为 处达到最高,高度为 ,水柱落地处离池
中心 ,水管长度应为_______.
2.25m
【解析】 以池的中心为原点,竖直安装的水管为 轴,与水管垂直的水
平线为 轴建立平面直角坐标系.因为在距池中心的水平距离为 处达
到最高,高度为 ,所以设抛物线的表达式为
(顶点式),将 代入,得 ,
所以该抛物线的表达式为 .令 ,则
,故水管长度为 .
3.[2022安丘一模]如图1是古代的一种远程攻击武器,发射出去的石块的运
动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将此
武器发射点置于山坡底部 处,山坡上有一点 ,点 与点 的水平距离
为30米且与地面的竖直距离为3米, 是高度为2.8米的防御墙.若以点
为原点,建立如图2所示的平面直角坐标系.
图1
图2
(1)石块运动轨迹所在抛物线的表达式为_ ________________;
;
【解析】 设石块的运动轨迹所在抛物线的表达式为 ,
把 代入,得 ,解得 ,
,即 .
(2)石块____飞越防御墙 (填“能”或“不能”).
能
【解析】 把 代入 ,得 ,
, 石块能飞越防御墙 .
4.教材P28练习变式 如图,隧道的截面由抛物线和长
方形构成,长方形的长是 ,宽是 .按照图中
所示的平面直角坐标系,抛物线可用
表示,且抛物线上的点 到墙面
的水平距离为 ,到地面 的距离为 .
(1)求该抛物线对应的二次函数的表达式,并计算出拱顶 到地面
的距离.
解:由题意得点 的坐标为 ,点 的坐标为 ,
, 两点在抛物线 上,
解得
该抛物线对应的二次函数的表达式为 .
,
拱顶 到地面 的距离为 .
(2)一辆货运汽车载一长方体集装箱后高为 ,宽为 ,如果隧道
内设双向行车道,那么这辆货车能否安全通过?
由题意得这辆货车最外侧与地面 的交点为 或 ,
当 或 时, , ,
这辆货车能安全通过.
【解题通法】
判断汽车能否从隧道下通过
(1)固定汽车的宽,判断隧道是否够高(即已知 的值,根据函数
表达式求出 的值,比较限制的高与 值的大小);(2)固定汽车的高,
判断隧道是否够宽(即已知 的值,根据函数表达式求出 的值,比较限
制的宽与 值的大小).
26.3 实践与探索
课时1 探索生活中的抛物线形问题
过能力 学科关键能力构建
1.[2022黄冈三模]如图1,“东方之门”通过简单的几何曲线处理,将传统文
化与现代建筑融为一体,最大程度地传承了苏州的历史文化.如图2,“门”
的内侧曲线呈抛物线形,已知其底部宽度为 ,高度为 ,则离
地面 处的水平宽度(即 的长)为( )
图1
图2
C
A. B. C. D.
【解析】 如图,建立平面直角坐标系,易得 ,
, .设抛物线的表达式为
,将 代入,得
,解得 , 抛物线的表
达式为 .将 代入,得
,解得 , , ,
.
2.教材P34复习题 变式 株洲五桥主桥主孔为拱梁钢构组合体系,如图
1.小明在五桥观光,发现拱梁的路面部分有均匀排列着的9根支柱,他回
家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)为10米,于是
他建立了如图2所示的平面直角坐标系,将余下的8根支柱的高度都算出来
了,你认为中柱右边第二根支柱的高度是( )
图1
图2
D
A.7米 B.7.6米 C.8米 D.8.4米
【解析】 根据题意可得点 的坐标是 ,设抛物线对应的二次函数的表达式为 ,将点 的坐标代入 ,得 ,解得 ,所以该抛物线对应的函数表达式为
. 可设中柱右边第二根支柱上端点的坐标为 ,于是
,所以中柱右边第二根支柱的高度是 (米).
3.新情境[2023长春中考]2023年5月28日, 商业首航完成——中国民
航商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过
隆重的“水门礼”(寓意“接风洗尘”,是国际民航中高级别的礼仪).如图1,
在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水
柱近似看作形状相同的抛物线的一部分.如图2,当两辆消防车喷水口 ,
的水平距离为80米时,两条水柱在抛物线的顶点 处相遇,此时相遇
点 距地面20米,喷水口 , 距地面均为4米.若两辆消防车同时后退10
米,两条水柱的形状及喷水口 , 到地面的距离均保持不变,则此时
两条水柱相遇点 距地面____米.
19
图1
图2
【解析】 由题意可知, , , .设抛物线的表达
式为 ,将点 的坐标代入 ,解得
, 消防车同时后退10米, 抛物线
向左(右)平移10米,平移后抛物线的表达式为
,令 ,解得 .
素养提升
4.新考法 应用意识[2023贵州中考]如图1,是一座抛物线形拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图2),抛物线的顶点在 处,对称轴 与水平线 垂直, ,点 在抛物线上,且点 到对称轴的距离 ,点 在抛物线上,点 到对称轴的距离是1.
图1
图2
备用图
(1)求该抛物线的表达式;
解:设抛物线的表达式为 ,
把点 的坐标代入,得 ,解得 ,
该抛物线的表达式为 .
(2)如图2,为更加稳固,小星想在 上找一点 ,加装拉杆 , ,
同时使拉杆的长度之和最短,请你帮小星找到点 的位置并求出坐标;
【解析】 解题思路:作点 关于 轴的对称点 ,连接 交 于点 , 则点 即所求;
如图,作点 关于 轴的对称点 ,则 ,连接 交 于点 ,则点 即所求.
把 代入 ,得 ,
.
设直线 的表达式为 ,
解得 .
令 ,得 , 点 的坐标为 .
(3)为了造型更加美观,小星重新设计抛物线,其表达式为
,当 时,函数 的值总大于等于
9.求 的取值范围.
【解析】 解题思路:分 , ,
三种情况讨论,结合二次函数的图象和性质,列不等式求得
的取值范围.
,
抛物线的对称轴为直线 ,顶点坐标为 .
①当 时,得 ,
解得 , .
②当 时,由 ,得 ,
(抛物线开口向下,点离对称轴的距离越远,对应的函数值越小),解得 , .
由 ,得 ,
,解得 , .
故当 时,都成立.
③当 时,得 ,
解得 , .
综上所述, 的取值范围为 .
