第十四章《三角形》(基础过关测试卷)(含解析)七年级数学下册沪教版
文档属性
| 名称 | 第十四章《三角形》(基础过关测试卷)(含解析)七年级数学下册沪教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览




文档简介
第十四章《三角形》(基础过关测试卷)
一、单选题(共6小题,每小题4分,共24分)
1.下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门
B.自行车的三角形车架
C.斜钉一根木条的长方形窗框
D.照相机的三脚架
2.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8 B.7 C.6 D.5
3.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
4.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD B.OC=OD C.∠CPO=∠DPO D.PC=PE
5.如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为( )
A.2 B.5 C.8 D.11
6.已知,如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下四个结论:①AD=BE;②△CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE.其中正确的结论是( )
A.①、② B.③、④ C.①、②、③ D.①、②、④
二、填空题(共12小题,每小题4分,共48分)
7.等腰△ABC,AB=AC,AD平分∠BAC交BC于D,如果BC=6,则BD= .
8.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
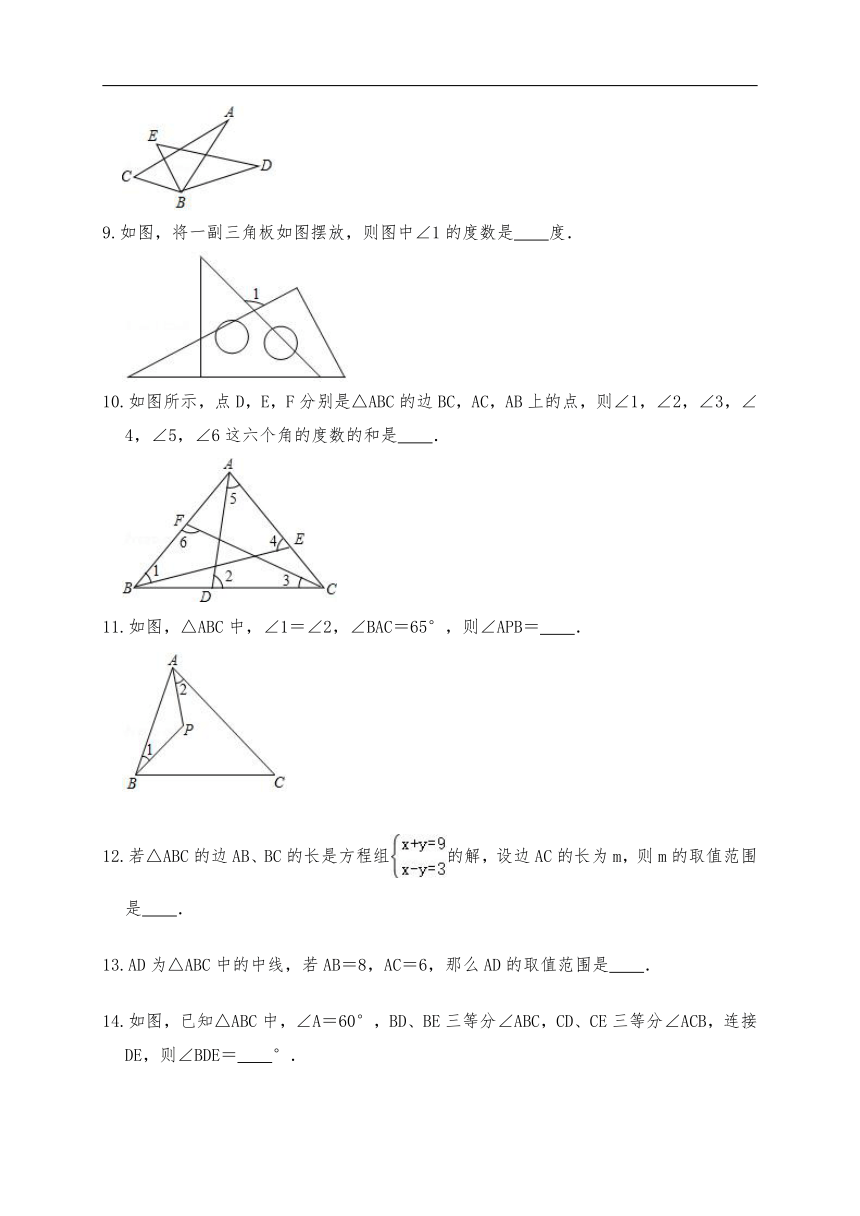
9.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
10.如图所示,点D,E,F分别是△ABC的边BC,AC,AB上的点,则∠1,∠2,∠3,∠4,∠5,∠6这六个角的度数的和是 .
11.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
12.若△ABC的边AB、BC的长是方程组的解,设边AC的长为m,则m的取值范围是 .
13.AD为△ABC中的中线,若AB=8,AC=6,那么AD的取值范围是 .
14.如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE= °.
15.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
16.已知等腰三角形的两边长分别为x和y,且x和y满足|x﹣3|+(y﹣1)2=0,则这个等腰三角形的周长为 .
17.如图,△ABC中,BE、CD分别平分∠ABC、∠ACB,并相交于点O,∠BOC=140°,则∠A= °.
18.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE.
(1)如图1,当CE∥AB时,若∠BAD=35°,则∠DEC 度;
(2)如图2,设∠BAC=α(90°<α<180°),在点D运动过程中,当DE⊥BC时,∠DEC= .(用含α的式子表示)
三、解答题(共78分)
19.如图,在△ABC和△DCB中,AB⊥AC,CD⊥BD,AB=DC,AC与BD交于点O.求证:AC=BD.
20.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
21.已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数.
(1)求c边的长;
(2)判断△ABC的形状.
22.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
23.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
24.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
25.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN
(1)求证:AM=BN;
(2)分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系(不需证明);
(3)如图4,当BM=AB时,证明:MN⊥AB.
答案
一、单选题
1.A
【分析】利用三角形的稳定性进行解答.
【解答】解:由四边形组成的伸缩门是利用了四边形的不稳定性,
而A、C、D选项都是利用了三角形的稳定性,
故选:A.
2.B
【分析】利用已知条件证明△ADE≌△ADC(SAS),得到ED=CD,从而BC=BD+CD=DE+BD=5,即可求得△BDE的周长.
【解答】解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故选:B.
3.D
【分析】利用SAS定理判定△ABC≌△DEC即可.
【解答】证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
4.D
【分析】根据AAS证明△POD≌△POC(AAS),可得结论.
【解答】解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
5.C
【分析】由“AAS”可证△BEF≌△CED,可得EF=DE,BF=CD=3,由线段垂直平分线的性质可得AD=AF=8.
【解答】解:∵E为BC的中点,
∴BE=EC,
∵AB∥CD,
在△BEF与△CED中,
,
∴△BEF≌△CED(AAS)
∴EF=DE,BF=CD=3,
∴AF=AB+BF=8,
∵AE⊥DE,EF=DE,
∴AF=AD=8,
故选:C.
6.D
【分析】先由SAS判定△ACD≌△BCE,证得①正确;再由ASA证△ACP≌△BCQ,得到CP=CQ,②正确,同理证得CM=CN,得到④正确;易得③不正确.
【解答】解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠BCD=∠BCD+∠ECD,∠BCD=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,故①正确;
∠CAD=∠CBE,
∵∠BCA=∠BCD=60°,AC=BC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
又∵∠PCQ=60°,
∴△CPQ是等边三角形,故②正确;
过C作CM⊥BE于M,CN⊥AD于N,
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵CD=CE,∠CND=∠CMA=90°,
∴△CDN≌△CEM(AAS),
∴CM=CN,
∵CM⊥BE,CN⊥AD,
∴OC平分∠AOE,故④正确;
当AC=CE时,AP平分∠BAC,
则∠PAC=30°,此时∠APC=180°﹣30°﹣60°=90°,
则AD⊥BC,故③不正确;
故选:D.
二、填空题
7.3
【分析】根据等腰三角形的三线合一解答即可.
【解答】解:∵AB=AC,AD平分∠BAC,
∴BD=CD=BC=3,
故答案为:3.
8.13
【分析】根据全等三角形的性质求出BC,根据三角形的面积公式计算,得到答案.
【解答】解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
9.105
【分析】根据三角形的外角性求出∠2,根据补角的概念求出∠1.
【解答】解:由三角形的外角性质控可知,∠2=30°+45°=75°,
∴∠1=180°﹣∠2=105°,
故答案为:105.
10.360°
【分析】利用三角形的外角的性质把这六个角转化到一个四边形中,即可求得结果.
【解答】解:不妨设AD和CF交于点M,BE和CF交于点N,
则∠AMC=∠2+∠3,∠ENF=∠1+∠6,
而∠AMC+∠ENF+∠4+∠5=360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
故答案为:360°.
11.115°
【分析】依据∠1=∠2,∠BAC=∠BAP+∠1=65°,即可得出∠BAP+∠2=65°,进而得到△ABP中,∠APB=180°﹣65°=115°.
【解答】解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
12.3<m<9
【分析】直接利用三角形三边关系得出答案.
【解答】解:∵△ABC的边AB、BC的长是方程组的解,边AC的长为m,
∴m的取值范围是:3<m<9,
故答案为:3<m<9.
13.1<AD<7
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系即可求解.
【解答】解:延长AD至E,使DE=AD,连接CE.
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB.
在△ACE中,CE﹣AC<AE<CE+AC,
即2<2AD<14,
∴1<AD<7,
故答案为:1<AD<7.
14.50
【分析】根据三角形内角和定理和三等分角的意义求解即可.
【解答】解:∵BD、BE三等分∠ABC,
∴∠DBC=∠ABC;
又∵CD、CE三等分∠ACB,
∴∠DCB=∠ACB;
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BDC=180°﹣(180°﹣∠A)=60°+∠A,
∵∠A=60°,
∴∠BDC=60°+×60°=100°,
∵BE,CE是△BDC的角平分线,
∴ED平分∠BDC,
∴∠BDE=∠BDC=50°,
故答案为:50.
15.①③④
【分析】①根据已知条件可以证明在△ABE和△ACF全等,即可得∠1=∠2;
②没有条件可以证明CD=DN,即可判断;
③结合①和已知条件即可得△ACN≌△ABM;
④根据△ABE≌△ACF,可得BE=CF,
【解答】解:①在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.
∴①正确;
没有条件可以证明CD=DN,
∴②错误;
∵△ABE≌△ACF,
∴AB=AC,
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),
∴③正确;
∵△ABE≌△ACF,
∴BE=CF,
∴④正确.
∴其中正确的结论有①③④.
故答案为:①③④.
16.7
【分析】根据非负数的性质求得x、y的值,然后得到三角形的三边长,接下来,利用三角形的三边关系进行验证,最后求得三角形的周长即可.
【解答】解:∵|x﹣3|+(y﹣1)2=0,
∴x=3,y=1.
当腰长为3时,三边长为3、3、1,周长=3+3+1=7;
当腰长为1时,三边长为3、1、1,1+1<3,不能组成三角形.
故答案为:7.
17.100
【分析】先根据BO平分∠ABC,CO平分∠ACB,可得∠ABC=2∠1,∠ACB=2∠2,再根据三角形内角和定理计算出∠1+∠2的度数,进而得到∠ABC+∠ACB,即可算出∠A的度数.
【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠BOC=140°,
∴∠1+∠2=180°﹣140°=40°,
∴∠ABC+∠ACB=2×40°=80°,
∴∠A=180°﹣80°=100°,
故答案为:100
18.【第1空】=25
【第2空】α-90°
【分析】(1)根据已知条件得到∠BAD=∠CAE,根据全等三角形的性质得到∠B=∠ACE,根据平行线的性质得到∠BAC=∠ACE,推出△ABC是等边三角形,得到∠BAC=∠DAE=∠ACB=∠ACE=60°,求得△DAE是等边三角形,于是得到结论;
(2)根据等腰三角形的性质得到∠B=∠ACB=(180°﹣α)=90°﹣,根据全等三角形的性质得到∠B=∠ACE=90°﹣,求得∠DCE=2(90°﹣)=180°﹣α,根据三角形的内角和即可得到结论.
【解答】解:(1)∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣35°﹣60°﹣60°=25°,
故答案为:25;
(2)连接CE,
∵∠BAC=α,AB=AC,
∴∠B=∠ACB=(180°﹣α)=90°﹣,
∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=90°﹣,
∴∠DCE=2(90°﹣)=180°﹣α,
∵DE⊥BC,
∴∠CDE=90°,
∴∠DEC=90°﹣∠DCE=α﹣90°.
故答案为:α﹣90°.
三、解答题
19.证明:∵AB⊥AC,CD⊥BD,
∴∠A=∠D=90°,
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL).
∴AC=BD.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AFD=∠CEB=90°,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
21.解:(1)∵a,b,c是△ABC的三边,a=4,b=6,
∴2<c<10,
∵三角形的周长是小于18的偶数,
∴2<c<8,
∴c=4或6;
(2)当c=4或6时,△ABC的形状都是等腰三角形.
22.解:(1)方法一:(m﹣n)2,
方法二:(m+n)2﹣4mn,
故答案为:(m﹣n)2;(m+n)2﹣4mn;
(2)(m﹣n)2=(m+n)2﹣4mn;
(3)当p+q=9,pq=7时,(p﹣q)2=(p+q)2﹣4pq=92﹣4×7=81﹣28=53.
23.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
24.解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,,
解得;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得;
综上所述,存在或使得△ACP与△BPQ全等.
25.(1)证明:∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,
∴∠APM=∠BPN.
在△APM≌△PBN中
,
∴△APM≌△PBN(SAS),
∴AM=BN.
(2)解:图2中BN=AB+BM;
图3中BN=BM﹣AB.
(3)证明:∵△PAB和△PMN是等边三角形,
∴∠ABP=∠PMN=60°,AB=PB,
∴∠PBM=120°,
∵BM=AB=PB,
∴∠BMP=30°,
∴∠BMN=∠PMN+∠BMP=90°,
∴MN⊥AB.
一、单选题(共6小题,每小题4分,共24分)
1.下列设计的原理不是利用三角形的稳定性的是( )
A.由四边形组成的伸缩门
B.自行车的三角形车架
C.斜钉一根木条的长方形窗框
D.照相机的三脚架
2.如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为( )
A.8 B.7 C.6 D.5
3.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
4.如图,OP平分∠AOB,PC⊥OA于点C,PD⊥OB于点D,延长CP,DP交OB,OA于点E,F.下列结论错误的是( )
A.PC=PD B.OC=OD C.∠CPO=∠DPO D.PC=PE
5.如图,在四边形ABCD中,AB∥DC,E为BC的中点,连接DE、AE,AE⊥DE,延长DE交AB的延长线于点F.若AB=5,CD=3,则AD的长为( )
A.2 B.5 C.8 D.11
6.已知,如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下四个结论:①AD=BE;②△CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE.其中正确的结论是( )
A.①、② B.③、④ C.①、②、③ D.①、②、④
二、填空题(共12小题,每小题4分,共48分)
7.等腰△ABC,AB=AC,AD平分∠BAC交BC于D,如果BC=6,则BD= .
8.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
9.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
10.如图所示,点D,E,F分别是△ABC的边BC,AC,AB上的点,则∠1,∠2,∠3,∠4,∠5,∠6这六个角的度数的和是 .
11.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
12.若△ABC的边AB、BC的长是方程组的解,设边AC的长为m,则m的取值范围是 .
13.AD为△ABC中的中线,若AB=8,AC=6,那么AD的取值范围是 .
14.如图,已知△ABC中,∠A=60°,BD、BE三等分∠ABC,CD、CE三等分∠ACB,连接DE,则∠BDE= °.
15.如图,EB交AC于点M,交CF于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②CD=DN;③△ACN≌△ABM;④BE=CF.其中正确的结论有 .(填序号)
16.已知等腰三角形的两边长分别为x和y,且x和y满足|x﹣3|+(y﹣1)2=0,则这个等腰三角形的周长为 .
17.如图,△ABC中,BE、CD分别平分∠ABC、∠ACB,并相交于点O,∠BOC=140°,则∠A= °.
18.如图,在△ABC中,AB=AC,D为线段BC上一动点(不与点B、C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接CE.
(1)如图1,当CE∥AB时,若∠BAD=35°,则∠DEC 度;
(2)如图2,设∠BAC=α(90°<α<180°),在点D运动过程中,当DE⊥BC时,∠DEC= .(用含α的式子表示)
三、解答题(共78分)
19.如图,在△ABC和△DCB中,AB⊥AC,CD⊥BD,AB=DC,AC与BD交于点O.求证:AC=BD.
20.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F,求证:BE=DF.
21.已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数.
(1)求c边的长;
(2)判断△ABC的形状.
22.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图②拼成一个正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积;
方法一: ;
方法二: ;
(2)观察图②,请直接写出下列三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
23.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
24.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
25.如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN
(1)求证:AM=BN;
(2)分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系(不需证明);
(3)如图4,当BM=AB时,证明:MN⊥AB.
答案
一、单选题
1.A
【分析】利用三角形的稳定性进行解答.
【解答】解:由四边形组成的伸缩门是利用了四边形的不稳定性,
而A、C、D选项都是利用了三角形的稳定性,
故选:A.
2.B
【分析】利用已知条件证明△ADE≌△ADC(SAS),得到ED=CD,从而BC=BD+CD=DE+BD=5,即可求得△BDE的周长.
【解答】解:∵AD是∠BAC的平分线,
∴∠EAD=∠CAD
在△ADE和△ADC中,
,
∴△ADE≌△ADC(SAS),
∴ED=CD,
∴BC=BD+CD=DE+BD=5,
∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.
故选:B.
3.D
【分析】利用SAS定理判定△ABC≌△DEC即可.
【解答】证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
4.D
【分析】根据AAS证明△POD≌△POC(AAS),可得结论.
【解答】解:∵OP平分∠AOB,
∴∠POD=∠POC,
∵PD⊥OB,PC⊥OA,
∴∠PCO=∠PDO,
在△POD和△POC中,
,
∴△POC≌△POD(AAS),
∴PC=PD,OC=OD,∠CPO=∠DPO,故A,B,C正确;
故选:D.
5.C
【分析】由“AAS”可证△BEF≌△CED,可得EF=DE,BF=CD=3,由线段垂直平分线的性质可得AD=AF=8.
【解答】解:∵E为BC的中点,
∴BE=EC,
∵AB∥CD,
在△BEF与△CED中,
,
∴△BEF≌△CED(AAS)
∴EF=DE,BF=CD=3,
∴AF=AB+BF=8,
∵AE⊥DE,EF=DE,
∴AF=AD=8,
故选:C.
6.D
【分析】先由SAS判定△ACD≌△BCE,证得①正确;再由ASA证△ACP≌△BCQ,得到CP=CQ,②正确,同理证得CM=CN,得到④正确;易得③不正确.
【解答】解:∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠BCD=∠BCD+∠ECD,∠BCD=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,故①正确;
∠CAD=∠CBE,
∵∠BCA=∠BCD=60°,AC=BC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
又∵∠PCQ=60°,
∴△CPQ是等边三角形,故②正确;
过C作CM⊥BE于M,CN⊥AD于N,
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵CD=CE,∠CND=∠CMA=90°,
∴△CDN≌△CEM(AAS),
∴CM=CN,
∵CM⊥BE,CN⊥AD,
∴OC平分∠AOE,故④正确;
当AC=CE时,AP平分∠BAC,
则∠PAC=30°,此时∠APC=180°﹣30°﹣60°=90°,
则AD⊥BC,故③不正确;
故选:D.
二、填空题
7.3
【分析】根据等腰三角形的三线合一解答即可.
【解答】解:∵AB=AC,AD平分∠BAC,
∴BD=CD=BC=3,
故答案为:3.
8.13
【分析】根据全等三角形的性质求出BC,根据三角形的面积公式计算,得到答案.
【解答】解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
9.105
【分析】根据三角形的外角性求出∠2,根据补角的概念求出∠1.
【解答】解:由三角形的外角性质控可知,∠2=30°+45°=75°,
∴∠1=180°﹣∠2=105°,
故答案为:105.
10.360°
【分析】利用三角形的外角的性质把这六个角转化到一个四边形中,即可求得结果.
【解答】解:不妨设AD和CF交于点M,BE和CF交于点N,
则∠AMC=∠2+∠3,∠ENF=∠1+∠6,
而∠AMC+∠ENF+∠4+∠5=360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
故答案为:360°.
11.115°
【分析】依据∠1=∠2,∠BAC=∠BAP+∠1=65°,即可得出∠BAP+∠2=65°,进而得到△ABP中,∠APB=180°﹣65°=115°.
【解答】解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
12.3<m<9
【分析】直接利用三角形三边关系得出答案.
【解答】解:∵△ABC的边AB、BC的长是方程组的解,边AC的长为m,
∴m的取值范围是:3<m<9,
故答案为:3<m<9.
13.1<AD<7
【分析】延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系即可求解.
【解答】解:延长AD至E,使DE=AD,连接CE.
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB.
在△ACE中,CE﹣AC<AE<CE+AC,
即2<2AD<14,
∴1<AD<7,
故答案为:1<AD<7.
14.50
【分析】根据三角形内角和定理和三等分角的意义求解即可.
【解答】解:∵BD、BE三等分∠ABC,
∴∠DBC=∠ABC;
又∵CD、CE三等分∠ACB,
∴∠DCB=∠ACB;
∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°﹣∠A),
∴∠BDC=180°﹣(180°﹣∠A)=60°+∠A,
∵∠A=60°,
∴∠BDC=60°+×60°=100°,
∵BE,CE是△BDC的角平分线,
∴ED平分∠BDC,
∴∠BDE=∠BDC=50°,
故答案为:50.
15.①③④
【分析】①根据已知条件可以证明在△ABE和△ACF全等,即可得∠1=∠2;
②没有条件可以证明CD=DN,即可判断;
③结合①和已知条件即可得△ACN≌△ABM;
④根据△ABE≌△ACF,可得BE=CF,
【解答】解:①在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.
∴①正确;
没有条件可以证明CD=DN,
∴②错误;
∵△ABE≌△ACF,
∴AB=AC,
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),
∴③正确;
∵△ABE≌△ACF,
∴BE=CF,
∴④正确.
∴其中正确的结论有①③④.
故答案为:①③④.
16.7
【分析】根据非负数的性质求得x、y的值,然后得到三角形的三边长,接下来,利用三角形的三边关系进行验证,最后求得三角形的周长即可.
【解答】解:∵|x﹣3|+(y﹣1)2=0,
∴x=3,y=1.
当腰长为3时,三边长为3、3、1,周长=3+3+1=7;
当腰长为1时,三边长为3、1、1,1+1<3,不能组成三角形.
故答案为:7.
17.100
【分析】先根据BO平分∠ABC,CO平分∠ACB,可得∠ABC=2∠1,∠ACB=2∠2,再根据三角形内角和定理计算出∠1+∠2的度数,进而得到∠ABC+∠ACB,即可算出∠A的度数.
【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠BOC=140°,
∴∠1+∠2=180°﹣140°=40°,
∴∠ABC+∠ACB=2×40°=80°,
∴∠A=180°﹣80°=100°,
故答案为:100
18.【第1空】=25
【第2空】α-90°
【分析】(1)根据已知条件得到∠BAD=∠CAE,根据全等三角形的性质得到∠B=∠ACE,根据平行线的性质得到∠BAC=∠ACE,推出△ABC是等边三角形,得到∠BAC=∠DAE=∠ACB=∠ACE=60°,求得△DAE是等边三角形,于是得到结论;
(2)根据等腰三角形的性质得到∠B=∠ACB=(180°﹣α)=90°﹣,根据全等三角形的性质得到∠B=∠ACE=90°﹣,求得∠DCE=2(90°﹣)=180°﹣α,根据三角形的内角和即可得到结论.
【解答】解:(1)∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠BAC=∠B,
∴AC=BC,
∴△ABC是等边三角形,
∴∠BAC=∠DAE=∠ACB=∠ACE=60°,
∴△DAE是等边三角形,
∴∠AED=60°,
∴∠DEC=180°﹣35°﹣60°﹣60°=25°,
故答案为:25;
(2)连接CE,
∵∠BAC=α,AB=AC,
∴∠B=∠ACB=(180°﹣α)=90°﹣,
∵∠DAE=∠BAC,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=90°﹣,
∴∠DCE=2(90°﹣)=180°﹣α,
∵DE⊥BC,
∴∠CDE=90°,
∴∠DEC=90°﹣∠DCE=α﹣90°.
故答案为:α﹣90°.
三、解答题
19.证明:∵AB⊥AC,CD⊥BD,
∴∠A=∠D=90°,
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL).
∴AC=BD.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE.
又∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AFD=∠CEB=90°,
在△AFD和△CEB中,
∴△AFD≌△CEB(AAS),
∴BE=DF.
21.解:(1)∵a,b,c是△ABC的三边,a=4,b=6,
∴2<c<10,
∵三角形的周长是小于18的偶数,
∴2<c<8,
∴c=4或6;
(2)当c=4或6时,△ABC的形状都是等腰三角形.
22.解:(1)方法一:(m﹣n)2,
方法二:(m+n)2﹣4mn,
故答案为:(m﹣n)2;(m+n)2﹣4mn;
(2)(m﹣n)2=(m+n)2﹣4mn;
(3)当p+q=9,pq=7时,(p﹣q)2=(p+q)2﹣4pq=92﹣4×7=81﹣28=53.
23.(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
24.解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,,
解得;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得;
综上所述,存在或使得△ACP与△BPQ全等.
25.(1)证明:∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,
∴∠APM=∠BPN.
在△APM≌△PBN中
,
∴△APM≌△PBN(SAS),
∴AM=BN.
(2)解:图2中BN=AB+BM;
图3中BN=BM﹣AB.
(3)证明:∵△PAB和△PMN是等边三角形,
∴∠ABP=∠PMN=60°,AB=PB,
∴∠PBM=120°,
∵BM=AB=PB,
∴∠BMP=30°,
∴∠BMN=∠PMN+∠BMP=90°,
∴MN⊥AB.
