第5单元三角形测试卷(含答案)2023-2024学年数学四年级下册人教版
文档属性
| 名称 | 第5单元三角形测试卷(含答案)2023-2024学年数学四年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 442.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览

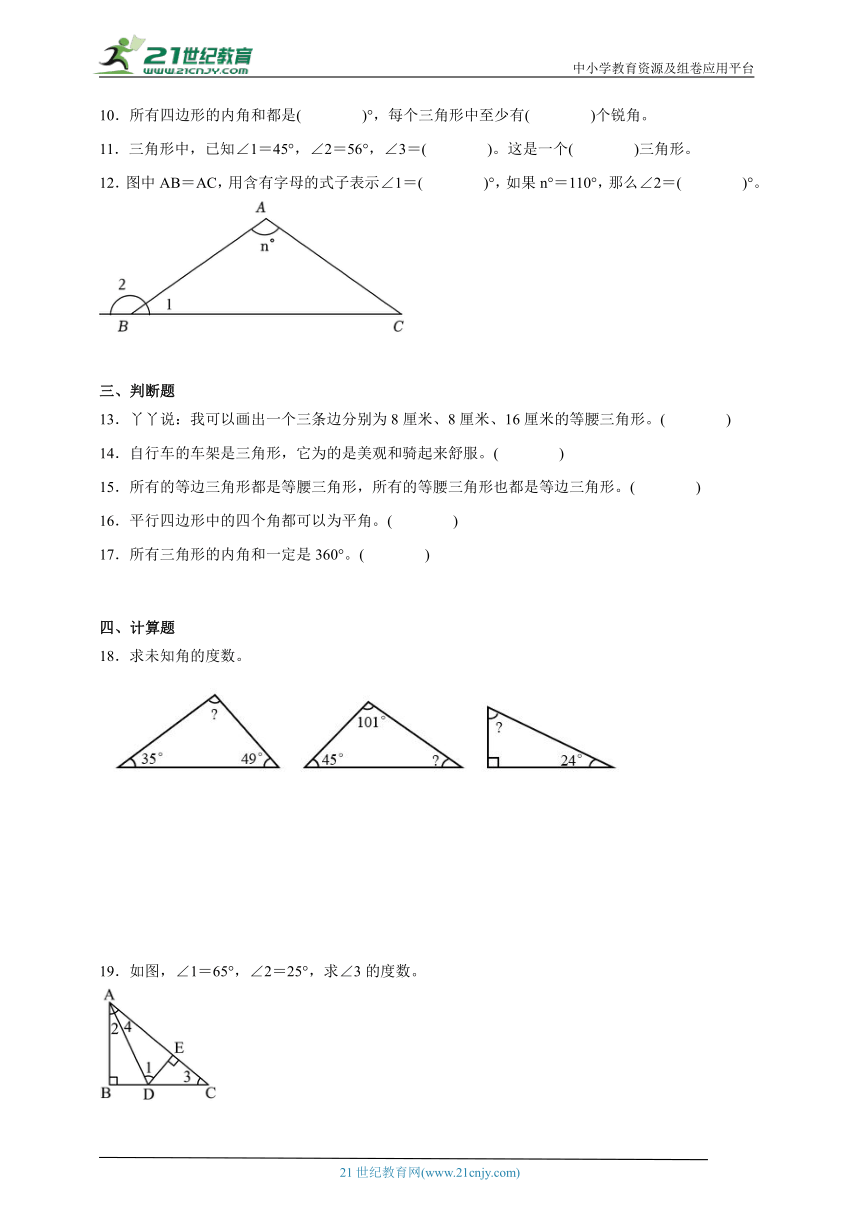



文档简介
中小学教育资源及组卷应用平台
第5单元三角形测试卷2023-2024学年数学四年级下册人教版
一、选择题
1.下面三组小棒,不能围成三角形的是( )。
A.3cm,4cm,5cm B.3cm,4cm,4cm C.3cm,3cm,6cm
2.一个三角形有一个角是45°,这个三角形不可能是( )。
A.等边三角形 B.直角三角形 C.钝角三角形
3.用三根长度为整厘米数的小棒围成一个三角形,如果其中两根小棒分别长、,那么第三根小棒最短是( )cm。
A.3 B.9 C.17
4.一个六边形的内角和是( )。
A.360° B.720° C.540°
5.下图是由一个等边三角形和一个任意三角形拼成的图形(三角形的边为整厘米数),拼成图形的周长最短是( )厘米。
A.21 B.22 C.27
6.任意大小的直角三角形中,两个锐角的和一定( )。
A.大于90° B.小于90° C.等于90°
二、填空题
7.把一根彩带平均截成3段,围成一个三角形,所围成三角形是( )三角形,它的每个角都是( )度。
8.如图,一块三角形纸片被撕去了一个角。这个角是( )度,原来这块纸片的形状是( )三角形。
9.已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是( )cm。
10.所有四边形的内角和都是( )°,每个三角形中至少有( )个锐角。
11.三角形中,已知∠1=45°,∠2=56°,∠3=( )。这是一个( )三角形。
12.图中AB=AC,用含有字母的式子表示∠1=( )°,如果n°=110°,那么∠2=( )°。
三、判断题
13.丫丫说:我可以画出一个三条边分别为8厘米、8厘米、16厘米的等腰三角形。( )
14.自行车的车架是三角形,它为的是美观和骑起来舒服。( )
15.所有的等边三角形都是等腰三角形,所有的等腰三角形也都是等边三角形。( )
16.平行四边形中的四个角都可以为平角。( )
17.所有三角形的内角和一定是360°。( )
四、计算题
18.求未知角的度数。
19.如图,∠1=65°,∠2=25°,求∠3的度数。
五、作图题
20.在如图的格子图上分别画一个钝角三角形、一个锐角三角形和一个等腰直角三角形。
六、解答题
21.盖房子时,在窗框未安装好之前,为了防止窗框变形,木工师傅常在窗框上斜钉一根木条,如果你是木工师傅,这根木条该怎样钉?在下图中画出来并说明理由。
22.一块等腰三角形的菜地,已知两条边分别长是79米和39米,如果在它的周围用篱笆围一圈,至少要用篱笆多少米?
23.一个等边三角形的花坛,边长30米,小明每天绕着花坛跑15圈,小明每天要跑多少米?
24.在一个直角三角形中,较大锐角的度数是较小锐角的4倍,较大锐角的度数是多少度?
25.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。金字塔每个侧面的底角大约是多少度?
参考答案:
1.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3+4>5,则长3cm,4cm,5cm的三根小棒能围成三角形;
B.3+4>4,则长3cm,4cm,4cm的三根小棒能围成三角形;
C.3+3=6,则长3cm,3cm,6cm的三根小棒不能围成三角形;
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
2.A
【分析】三角形的内角和是180°;
等边三角形:三条边相等的三角形;等边三角形的三个角都相等;
直角三角形:有一个角是直角的三角形;
钝角三角形:有一个角是钝角的三角形。
【详解】A.等边三角形的三个角都是180°÷3=60°,所以一个角是45°的三角形不可能是等边三角形;
B.如果是直角三角形,三个角是45°、45°和90°,所以一个角是45°的三角形可能是直角三角形;
C.如果是钝角三角形,三个角可能是45°、35°和100°,所以一个角是45°的三角形可能是钝角三角形。
故答案为:A
【点睛】本题考查三角形的分类和三角形的内角和的应用。
3.A
【分析】三角形任意两边之差小于第三边,任意两边之和大于第三边,据此即可解答。
【详解】8+10=18(cm)
10-8=2(cm)
2cm<第三边<18cm,所以第三根小棒最短是3cm,最长是17cm。
故答案为:A
【点睛】熟悉三角形的三边关系,能够结合题意列出合理的不等式,是解答此题的关键。
4.B
【分析】多边形的内角和=(多边形的边数-2)×180°,六边形有6条边,依此计算并选择即可。
【详解】(6-2)×180°
=4×180°
=720°
一个六边形的内角和是720°。
故答案为:B
【点睛】熟练掌握多边形内角和的计算方法,是解答此题的关键。
5.B
【分析】观察上图可知,等边三角形的边长为7厘米,等边三角形的周长为7×3=21(厘米),由于三角形任意两边之和大于第三边,所以拼成的四边形的周长大于等边三角形的周长,即拼成的四边形的周长大于21厘米,最短是22厘米,据此即可解答。
【详解】根据分析可知,图中是由一个等边三角形和一个任意三角形拼成的图形(三角形的边为整厘米数),拼成图形的周长最短是22厘米。
故答案为:B
【点睛】本题主要考查学生对三角形三边间关系的掌握和灵活运用。
6.C
【分析】三角形内角和180°,直角90°,三角形内角和-直角度数=两个锐角的度数和,据此分析。
【详解】180°-90°=90°
任意大小的直角三角形中,两个锐角的和一定等于90°。
故答案为:C
【点睛】关键是熟悉直角三角形特点,明确三角形内角和。
7. 等边 60
【分析】三条边相等的三角形是等边三角形,等边三角形的三个角都相等,等于60度,据此即可解答。
【详解】把一根彩带平均截成3段,围成一个三角形,这个三角形的三条边都相等,所围成三角形是等边三角形,它的每个角都是60度。
【点睛】熟练掌握三角形的分类知识是解答本题的关键。
8. 66 等腰
【分析】三角形的内角和为180°,因此用180°减去另外两个角的度数之和,然后再根据三角形的分类标准分类即可,依此解答。
【详解】66°+48°=114°
180°-114°=66°
66°=66°
由此可知,这个角是66度,原来这块纸片的形状是等腰三角形或(锐角三角形)。
【点睛】解答此题的关键是要熟练掌握三角形的分类标准,等腰三角形的特点,以及熟记三角形的内角和度数。
9.14
【分析】根据三角形3条边之间的关系,在三角形中,任意两边之和大于底三边,因此可知,这个等腰三角形的底是2厘米,腰是6厘米,根据三角形的周长公式解答即可。
【详解】根据分析可知,三角形周长:
2+6+6
=8+6
=14(cm)
已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是14cm。
【点睛】本题主要考查三角形周长公式的灵活运用,等腰三角形的特征及应用,关键是明确:在三角形中,任意两边之和大于底三边。
10. 360 2
【分析】多边形的内角和=(多边形的边数-2)×180°,一个三个形的内角和是180°,依此解答即可。
【详解】(4﹣2)×180°
=2×180°
=360°;
所有四边形的内角和都是360°。
如果一个三角形中只有一个锐角,则另外两个角是两个直角或两个钝角或一个直角和一个钝角,那么这两个角的和就大于180°,因此每个三角形中至少有2个锐角。
【点睛】解答此题的关键是要熟练掌握多边形内角和的计算方法,以及熟记三角形的内角和度数。
11. 79° 锐角
【分析】根据三角形的内角和为180°可知,∠1+∠2+∠3=180°,则∠3=180°-∠1-∠2=79°。这三个角都是锐角,则这个三角形是锐角三角形。
【详解】∠3=180°-∠1-∠2=180°-45°-56°=79°
这是一个锐角三角形。
【点睛】本题考查三角形的内角和定理以及三角形的分类,关键是求出∠3的度数。
12. 145
【分析】由题意可知:AB=AC,所以△ABC是等腰三角形,且A为顶角,因此可根据等腰三角形的性质及三角形内角和定理,可知∠1和∠C相等,用(180°-n°)÷2即可求出∠1的度数,把n°=110°代入(180°-n°)÷2计算即可求出∠1的度数,最后用180°减去∠1的度数,即可求出∠2的度数。
【详解】因为AB=AC
所以△ABC是等腰三角形,
∠1=∠C
所以∠1
=(180°-n°)÷2
=°
如果n°=110°,
那么∠1为(180°-110°)÷2
=70°÷2
=35°
180°-35°=145°
用含有字母的式子表示∠1=°,如果n°=110°,那么∠2=145°。
【点睛】本题主要考查了等腰三角形的性质及三角形内角和定理等知识的应用,由已知条件判断出∠A为顶角是正确解答本题的关键。
13.×
【分析】根据三角形的性质,任意两边之和大于第三边可以判断得出答案。
【详解】(厘米)
,因此8厘米、8厘米、16厘米不能组成一个三角形。
故答案为:×
【点睛】本题主要考查了三角形任意两边之和大于第三边的性质。
14.×
【分析】根据三角形具有稳定性,解答此题即可。
【详解】自行车的车架是三角形,是利用三角形的稳定性特点,它为的是稳固;
所以原题说法错误。
故答案为:×
【点睛】熟练掌握三角形的特性,是解答此题的关键。
15.×
【分析】有两条边相等的三角形叫等腰三角形,三条边相等的三角形叫等边三角形,等边三角形是特殊的等腰三角形,所以等边三角形一定是等腰三角形,但等腰三角形不一定是等边三角形。
【详解】根据分析可知,等边三角形一定是等腰三角形,但等腰三角形不一定是等边三角形,原说法错误。
故答案为:×
【点睛】本题主要考查学生对等边三角形和等腰三角形定义和二者之间关系的掌握。
16.×
【分析】四边形的内角和为360°,如果平行四边形中的四个角为平角,则内角和为180°×4=720°,所以平行四边形的四个角不能为平角,据此即可解答。
【详解】根据分析可知,平行四边形中的四个角不能为平角,原说法错误。
故答案为:×
【点睛】本题主要考查学生对多边形内角和知识的掌握和灵活运用。
17.×
【分析】根据三角形的内角和等于180°,解答此题即可。
【详解】所有三角形的内角和一定是180°,所以原题的说法错误。
故答案为:×
【点睛】熟练掌握三角形的内角和,是解答此题的关键。
18.96°;34°;66°
【分析】三角形的内角和是180°,1直角=90°,因此用180°减另外两个角的度数之和即可,依此计算。
【详解】180°-(35°+49°)
=180°-84°
=96°
180°-(101°+45°)
=180°-146°
=34°
180°-(90°+24°)
=180°-114°
=66°
19.40°
【分析】∠2=25°,则在直角三角形ABD中,∠ADB=180°-90°-∠2=65°,∠1、∠ADB和∠EDC组成一个平角,则∠EDC=180°-65°-65°=50°,在直角三角形EDC中,∠3=180°-90°-∠EDC=40°。
【详解】在直角三角形ABD中,
∠ADB=180°-90°-25°
=90。-25。
=65°
则∠EDC=180°-65°-65°
=115。-65。
=50°
在直角三角形EDC中,
∠3=180°-90°-50°
=90。-50。
=40°
【点睛】此题考查了三角形内角和的灵活运用。
20.见详解
【分析】(1)要画一个钝角三角形,可先画一个钝角,然后将这个角的两边用线段连接起来即可。
(2)要画一个锐角三角形,可先画一个锐角,然后将这个角的两边用线段连接起来即可(需保证三个角都是锐角)。
(3)要画一个等腰直角三角形,可先画一个直角且直角的两条边的长度得一样,然后用线段将两边连接起来即可。
【详解】
21.画图见详解;原来的窗框是长边形,容易变形,这样钉木条,利用了三角形不容易变形的特性(稳定性)。
【分析】窗框为长方形,长方形容易变形,因此为了防止窗框变形,则应使窗框更加稳定,而三角形具有稳定性,依此画图并解答即可。
【详解】根据分析可知,如果我是木工师傅,这根木条应该这样钉:
理由:原来的窗框是长边形,容易变形,这样钉木条,利用了三角形不容易变形的特性(稳定性)。
【点睛】熟练掌握三角形的稳定性及应用是解答此题的关键。
22.197米
【分析】先根据构成三角形的特征,任意两边之和大于第三边,任意两边之差小于第三边,判断等腰三角形的两腰以及底边的长度,再把三边的长度相加即可,据此解答。
【详解】
所以三角形的两腰分别是79米、79米,底边是39米,
答:至少要用篱笆197米。
【点睛】熟练掌握等腰三角形的特征以及三角形周长的计算方法是解答本题的关键。
23.1350米
【分析】先根据边长计算出一圈的长度,等边三角形的三边相等,再用乘法计算出15圈跑了多少米,据此解答。
【详解】
答:小明每天要跑1350米。
【点睛】熟练掌握等边三角形的特征以及两位数乘两位数的计算方法并灵活运用是解答本题的关键。
24.72°
【分析】根据三角形的内角和为180°可知,直角三角形的两个锐角度数和是180°-90°=90°。较大锐角的度数是较小锐角的4倍,则较小锐角的5倍是90°,较小锐角是90°÷5=18°。用较小锐角的度数乘4,求出较大锐角的度数。
【详解】180°-90°=90°
90°÷(1+4)×4
=90°÷5×4
=18°×4
=72°
答:较大锐角的度数是72°。
【点睛】本题考查三角形的内角和定理和三角形的分类,关键是明确较小锐角的5倍是90°。
25.64度
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和一个顶角是52°,先求得两个底角的度数,进而求得它的一个底角的度数。
【详解】180°-52°=128°
128°÷2=64°
答:金字塔每个侧面的底角大约是64度。
【点睛】此题根据等腰三角形的特征和三角形的内角和解决。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元三角形测试卷2023-2024学年数学四年级下册人教版
一、选择题
1.下面三组小棒,不能围成三角形的是( )。
A.3cm,4cm,5cm B.3cm,4cm,4cm C.3cm,3cm,6cm
2.一个三角形有一个角是45°,这个三角形不可能是( )。
A.等边三角形 B.直角三角形 C.钝角三角形
3.用三根长度为整厘米数的小棒围成一个三角形,如果其中两根小棒分别长、,那么第三根小棒最短是( )cm。
A.3 B.9 C.17
4.一个六边形的内角和是( )。
A.360° B.720° C.540°
5.下图是由一个等边三角形和一个任意三角形拼成的图形(三角形的边为整厘米数),拼成图形的周长最短是( )厘米。
A.21 B.22 C.27
6.任意大小的直角三角形中,两个锐角的和一定( )。
A.大于90° B.小于90° C.等于90°
二、填空题
7.把一根彩带平均截成3段,围成一个三角形,所围成三角形是( )三角形,它的每个角都是( )度。
8.如图,一块三角形纸片被撕去了一个角。这个角是( )度,原来这块纸片的形状是( )三角形。
9.已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是( )cm。
10.所有四边形的内角和都是( )°,每个三角形中至少有( )个锐角。
11.三角形中,已知∠1=45°,∠2=56°,∠3=( )。这是一个( )三角形。
12.图中AB=AC,用含有字母的式子表示∠1=( )°,如果n°=110°,那么∠2=( )°。
三、判断题
13.丫丫说:我可以画出一个三条边分别为8厘米、8厘米、16厘米的等腰三角形。( )
14.自行车的车架是三角形,它为的是美观和骑起来舒服。( )
15.所有的等边三角形都是等腰三角形,所有的等腰三角形也都是等边三角形。( )
16.平行四边形中的四个角都可以为平角。( )
17.所有三角形的内角和一定是360°。( )
四、计算题
18.求未知角的度数。
19.如图,∠1=65°,∠2=25°,求∠3的度数。
五、作图题
20.在如图的格子图上分别画一个钝角三角形、一个锐角三角形和一个等腰直角三角形。
六、解答题
21.盖房子时,在窗框未安装好之前,为了防止窗框变形,木工师傅常在窗框上斜钉一根木条,如果你是木工师傅,这根木条该怎样钉?在下图中画出来并说明理由。
22.一块等腰三角形的菜地,已知两条边分别长是79米和39米,如果在它的周围用篱笆围一圈,至少要用篱笆多少米?
23.一个等边三角形的花坛,边长30米,小明每天绕着花坛跑15圈,小明每天要跑多少米?
24.在一个直角三角形中,较大锐角的度数是较小锐角的4倍,较大锐角的度数是多少度?
25.埃及金字塔的四个侧面的形状都是等腰三角形,每个等腰三角形的顶角约是52°。金字塔每个侧面的底角大约是多少度?
参考答案:
1.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.3+4>5,则长3cm,4cm,5cm的三根小棒能围成三角形;
B.3+4>4,则长3cm,4cm,4cm的三根小棒能围成三角形;
C.3+3=6,则长3cm,3cm,6cm的三根小棒不能围成三角形;
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
2.A
【分析】三角形的内角和是180°;
等边三角形:三条边相等的三角形;等边三角形的三个角都相等;
直角三角形:有一个角是直角的三角形;
钝角三角形:有一个角是钝角的三角形。
【详解】A.等边三角形的三个角都是180°÷3=60°,所以一个角是45°的三角形不可能是等边三角形;
B.如果是直角三角形,三个角是45°、45°和90°,所以一个角是45°的三角形可能是直角三角形;
C.如果是钝角三角形,三个角可能是45°、35°和100°,所以一个角是45°的三角形可能是钝角三角形。
故答案为:A
【点睛】本题考查三角形的分类和三角形的内角和的应用。
3.A
【分析】三角形任意两边之差小于第三边,任意两边之和大于第三边,据此即可解答。
【详解】8+10=18(cm)
10-8=2(cm)
2cm<第三边<18cm,所以第三根小棒最短是3cm,最长是17cm。
故答案为:A
【点睛】熟悉三角形的三边关系,能够结合题意列出合理的不等式,是解答此题的关键。
4.B
【分析】多边形的内角和=(多边形的边数-2)×180°,六边形有6条边,依此计算并选择即可。
【详解】(6-2)×180°
=4×180°
=720°
一个六边形的内角和是720°。
故答案为:B
【点睛】熟练掌握多边形内角和的计算方法,是解答此题的关键。
5.B
【分析】观察上图可知,等边三角形的边长为7厘米,等边三角形的周长为7×3=21(厘米),由于三角形任意两边之和大于第三边,所以拼成的四边形的周长大于等边三角形的周长,即拼成的四边形的周长大于21厘米,最短是22厘米,据此即可解答。
【详解】根据分析可知,图中是由一个等边三角形和一个任意三角形拼成的图形(三角形的边为整厘米数),拼成图形的周长最短是22厘米。
故答案为:B
【点睛】本题主要考查学生对三角形三边间关系的掌握和灵活运用。
6.C
【分析】三角形内角和180°,直角90°,三角形内角和-直角度数=两个锐角的度数和,据此分析。
【详解】180°-90°=90°
任意大小的直角三角形中,两个锐角的和一定等于90°。
故答案为:C
【点睛】关键是熟悉直角三角形特点,明确三角形内角和。
7. 等边 60
【分析】三条边相等的三角形是等边三角形,等边三角形的三个角都相等,等于60度,据此即可解答。
【详解】把一根彩带平均截成3段,围成一个三角形,这个三角形的三条边都相等,所围成三角形是等边三角形,它的每个角都是60度。
【点睛】熟练掌握三角形的分类知识是解答本题的关键。
8. 66 等腰
【分析】三角形的内角和为180°,因此用180°减去另外两个角的度数之和,然后再根据三角形的分类标准分类即可,依此解答。
【详解】66°+48°=114°
180°-114°=66°
66°=66°
由此可知,这个角是66度,原来这块纸片的形状是等腰三角形或(锐角三角形)。
【点睛】解答此题的关键是要熟练掌握三角形的分类标准,等腰三角形的特点,以及熟记三角形的内角和度数。
9.14
【分析】根据三角形3条边之间的关系,在三角形中,任意两边之和大于底三边,因此可知,这个等腰三角形的底是2厘米,腰是6厘米,根据三角形的周长公式解答即可。
【详解】根据分析可知,三角形周长:
2+6+6
=8+6
=14(cm)
已知一个等腰三角形的两条边长度分别是2cm、6cm,这个三角形的周长是14cm。
【点睛】本题主要考查三角形周长公式的灵活运用,等腰三角形的特征及应用,关键是明确:在三角形中,任意两边之和大于底三边。
10. 360 2
【分析】多边形的内角和=(多边形的边数-2)×180°,一个三个形的内角和是180°,依此解答即可。
【详解】(4﹣2)×180°
=2×180°
=360°;
所有四边形的内角和都是360°。
如果一个三角形中只有一个锐角,则另外两个角是两个直角或两个钝角或一个直角和一个钝角,那么这两个角的和就大于180°,因此每个三角形中至少有2个锐角。
【点睛】解答此题的关键是要熟练掌握多边形内角和的计算方法,以及熟记三角形的内角和度数。
11. 79° 锐角
【分析】根据三角形的内角和为180°可知,∠1+∠2+∠3=180°,则∠3=180°-∠1-∠2=79°。这三个角都是锐角,则这个三角形是锐角三角形。
【详解】∠3=180°-∠1-∠2=180°-45°-56°=79°
这是一个锐角三角形。
【点睛】本题考查三角形的内角和定理以及三角形的分类,关键是求出∠3的度数。
12. 145
【分析】由题意可知:AB=AC,所以△ABC是等腰三角形,且A为顶角,因此可根据等腰三角形的性质及三角形内角和定理,可知∠1和∠C相等,用(180°-n°)÷2即可求出∠1的度数,把n°=110°代入(180°-n°)÷2计算即可求出∠1的度数,最后用180°减去∠1的度数,即可求出∠2的度数。
【详解】因为AB=AC
所以△ABC是等腰三角形,
∠1=∠C
所以∠1
=(180°-n°)÷2
=°
如果n°=110°,
那么∠1为(180°-110°)÷2
=70°÷2
=35°
180°-35°=145°
用含有字母的式子表示∠1=°,如果n°=110°,那么∠2=145°。
【点睛】本题主要考查了等腰三角形的性质及三角形内角和定理等知识的应用,由已知条件判断出∠A为顶角是正确解答本题的关键。
13.×
【分析】根据三角形的性质,任意两边之和大于第三边可以判断得出答案。
【详解】(厘米)
,因此8厘米、8厘米、16厘米不能组成一个三角形。
故答案为:×
【点睛】本题主要考查了三角形任意两边之和大于第三边的性质。
14.×
【分析】根据三角形具有稳定性,解答此题即可。
【详解】自行车的车架是三角形,是利用三角形的稳定性特点,它为的是稳固;
所以原题说法错误。
故答案为:×
【点睛】熟练掌握三角形的特性,是解答此题的关键。
15.×
【分析】有两条边相等的三角形叫等腰三角形,三条边相等的三角形叫等边三角形,等边三角形是特殊的等腰三角形,所以等边三角形一定是等腰三角形,但等腰三角形不一定是等边三角形。
【详解】根据分析可知,等边三角形一定是等腰三角形,但等腰三角形不一定是等边三角形,原说法错误。
故答案为:×
【点睛】本题主要考查学生对等边三角形和等腰三角形定义和二者之间关系的掌握。
16.×
【分析】四边形的内角和为360°,如果平行四边形中的四个角为平角,则内角和为180°×4=720°,所以平行四边形的四个角不能为平角,据此即可解答。
【详解】根据分析可知,平行四边形中的四个角不能为平角,原说法错误。
故答案为:×
【点睛】本题主要考查学生对多边形内角和知识的掌握和灵活运用。
17.×
【分析】根据三角形的内角和等于180°,解答此题即可。
【详解】所有三角形的内角和一定是180°,所以原题的说法错误。
故答案为:×
【点睛】熟练掌握三角形的内角和,是解答此题的关键。
18.96°;34°;66°
【分析】三角形的内角和是180°,1直角=90°,因此用180°减另外两个角的度数之和即可,依此计算。
【详解】180°-(35°+49°)
=180°-84°
=96°
180°-(101°+45°)
=180°-146°
=34°
180°-(90°+24°)
=180°-114°
=66°
19.40°
【分析】∠2=25°,则在直角三角形ABD中,∠ADB=180°-90°-∠2=65°,∠1、∠ADB和∠EDC组成一个平角,则∠EDC=180°-65°-65°=50°,在直角三角形EDC中,∠3=180°-90°-∠EDC=40°。
【详解】在直角三角形ABD中,
∠ADB=180°-90°-25°
=90。-25。
=65°
则∠EDC=180°-65°-65°
=115。-65。
=50°
在直角三角形EDC中,
∠3=180°-90°-50°
=90。-50。
=40°
【点睛】此题考查了三角形内角和的灵活运用。
20.见详解
【分析】(1)要画一个钝角三角形,可先画一个钝角,然后将这个角的两边用线段连接起来即可。
(2)要画一个锐角三角形,可先画一个锐角,然后将这个角的两边用线段连接起来即可(需保证三个角都是锐角)。
(3)要画一个等腰直角三角形,可先画一个直角且直角的两条边的长度得一样,然后用线段将两边连接起来即可。
【详解】
21.画图见详解;原来的窗框是长边形,容易变形,这样钉木条,利用了三角形不容易变形的特性(稳定性)。
【分析】窗框为长方形,长方形容易变形,因此为了防止窗框变形,则应使窗框更加稳定,而三角形具有稳定性,依此画图并解答即可。
【详解】根据分析可知,如果我是木工师傅,这根木条应该这样钉:
理由:原来的窗框是长边形,容易变形,这样钉木条,利用了三角形不容易变形的特性(稳定性)。
【点睛】熟练掌握三角形的稳定性及应用是解答此题的关键。
22.197米
【分析】先根据构成三角形的特征,任意两边之和大于第三边,任意两边之差小于第三边,判断等腰三角形的两腰以及底边的长度,再把三边的长度相加即可,据此解答。
【详解】
所以三角形的两腰分别是79米、79米,底边是39米,
答:至少要用篱笆197米。
【点睛】熟练掌握等腰三角形的特征以及三角形周长的计算方法是解答本题的关键。
23.1350米
【分析】先根据边长计算出一圈的长度,等边三角形的三边相等,再用乘法计算出15圈跑了多少米,据此解答。
【详解】
答:小明每天要跑1350米。
【点睛】熟练掌握等边三角形的特征以及两位数乘两位数的计算方法并灵活运用是解答本题的关键。
24.72°
【分析】根据三角形的内角和为180°可知,直角三角形的两个锐角度数和是180°-90°=90°。较大锐角的度数是较小锐角的4倍,则较小锐角的5倍是90°,较小锐角是90°÷5=18°。用较小锐角的度数乘4,求出较大锐角的度数。
【详解】180°-90°=90°
90°÷(1+4)×4
=90°÷5×4
=18°×4
=72°
答:较大锐角的度数是72°。
【点睛】本题考查三角形的内角和定理和三角形的分类,关键是明确较小锐角的5倍是90°。
25.64度
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和一个顶角是52°,先求得两个底角的度数,进而求得它的一个底角的度数。
【详解】180°-52°=128°
128°÷2=64°
答:金字塔每个侧面的底角大约是64度。
【点睛】此题根据等腰三角形的特征和三角形的内角和解决。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
