物理人教版(2019)必修第一册3.5共点力的平衡 课件(共73张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册3.5共点力的平衡 课件(共73张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览




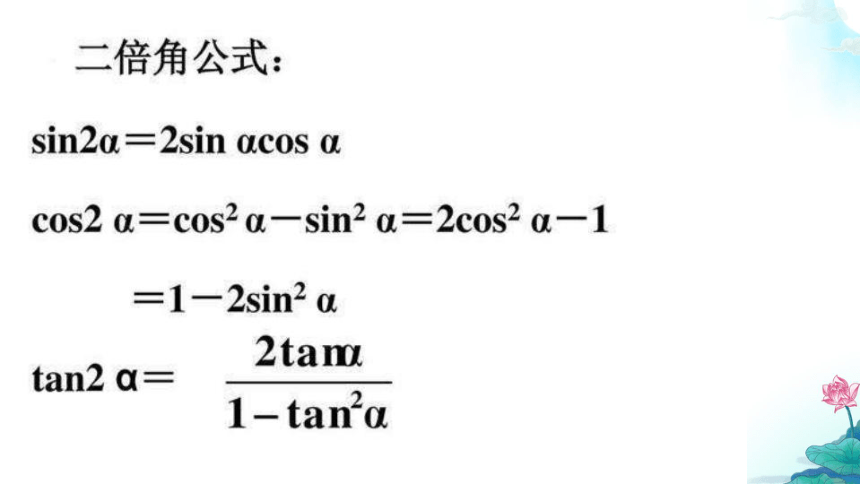






文档简介
(共73张PPT)
第三章 相互作用——力
第五节 共点力的平衡
数学知识的普及
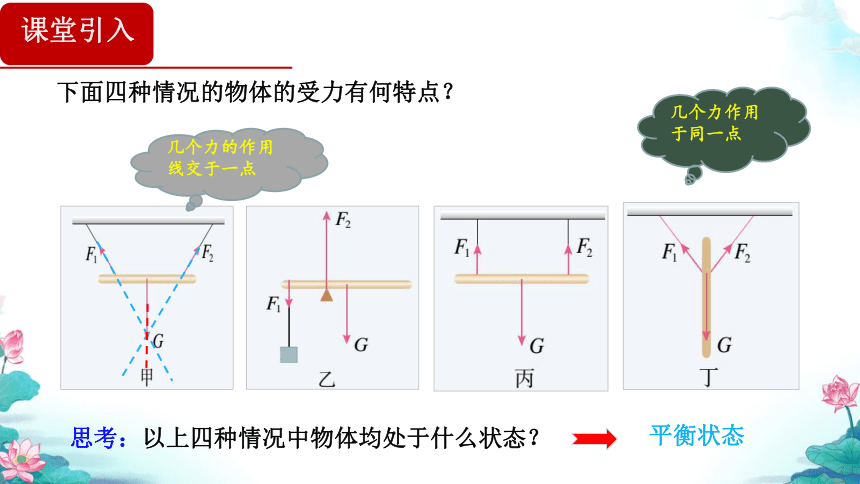
下面四种情况的物体的受力有何特点?
思考:以上四种情况中物体均处于什么状态?
几个力的作用线交于一点
几个力作用于同一点
课堂引入
平衡状态
G
FN
一、平衡状态
二力平衡时两个力:
大小相等,方向相反
G
FN
平衡状态:物体处于静止或者匀速直线运动的状态。
G
F1
F2
G
N
f
当物体受到多个力作用平衡时,它们的受力有何特点
F
f
N
G
合力等于零,即F合=0
一、平衡状态
平衡状态的运动学特征:v=0 或v不变,即:a=0
注意:保持静止和瞬时速度为0意义不同
平衡条件
共点力合力为0的具体表达形式
F合 = 0
物体受三个力:
三个力首尾相接构成一个闭合三角形
任意两个力的合力和第三个力是一对平衡力
正交分解:
Fx = 0
Fy = 0
物体受多个力时:
正交分解:
Fx = 0
Fy = 0
物体受两个力时:
一、平衡状态
可以举些例子吗?
【例题1】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
二、共点力平衡实例分析
A
B
C
方法一:正交分解法
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
F1
F2
二、共点力平衡实例分析
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等值反向
方法二:合成法
二、共点力平衡实例分析
FN
G
G’
Ff
A
B
C
θ
θ
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
G
Ff
FN
合成法:把物体所受的力合成为两个力,则这两个力大小相等、方向相反,并且在同一条直线上。
正交分解法:把物体所受的力在两个互相垂直的方向上分解,每个方向上合力都为0。
两种方法的特点:
二、共点力平衡实例分析
模型演示
1.确定研究对象;
2.对研究对象进行受力分析;
3.根据共点力的平衡条件列方程;
4.求解平衡方程;
5.讨论解的合理性和实际意义。
共点力平衡问题的解题步骤
二、共点力平衡实例分析
【例题2】如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
F3
F2
F1
二、共点力平衡实例分析
合成法
F3
F2
F1
F5
F3
F2
F1
F6
乙
丙
F3
F1
F2
F4
甲
对于三力平衡问题,可以选择任意的两个力进行合成。对甲:
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
二、共点力平衡实例分析
【例题3】如图示,BO为一轻杆,AO和CO为两段细绳,重物质量为m,在图示状态静止,求AO绳的张力.
45°
30°
正交分解法
T=G
N
F
x
y
Nx
Ny
Fx
Fy
受力特点:三个力互相不垂直,且夹角(方向)已知。
二、共点力平衡实例分析
受力特点:三个力互相不垂直,且夹角(方向)未知。
【例题4】如图,半径为R的光滑半球的正上方,离球面顶端距离为h的O点,用一根长为l的细线悬挂质量为m的小球,小球靠在半球面上.试求小球对球面压力的大小.
F
N
G
相似三角形法:力的三角形与空间三角形相似
T
二、共点力平衡实例分析
受力特点:三个力互相不垂直,且夹角(方向)未知。
【例题4】如图,半径为R的光滑半球的正上方,离球面顶端距离为h的O点,用一根长为l的细线悬挂质量为m的小球,小球靠在半球面上.试求小球对球面压力的大小.
F
N
G
相似三角形法:力的三角形与空间三角形相似
T
二、共点力平衡实例分析
【例题5】城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂。图为这类结构的一种简化模型。图中硬杆OB可绕通过B点且垂直于纸面的轴转动,钢索和杆的重量都可忽略。如果悬挂物的重量是G,角AOB 等于θ ,钢索AO对O点的拉力和杆OB对O点的支持力各是多大?
二、共点力平衡实例分析
方法一:解析法
水平方向:
竖直方向:
O点受力如图,对O点由共点力平衡条件,
方法2 用正交分解的方法求解。
二、共点力平衡实例分析
方法二:正交分解法
绳子的死结和活结
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
方法2 用正交分解的方法求解。
二、共点力平衡实例分析
方法2 用正交分解的方法求解。
处理平衡问题的常用方法
动态平衡问题是指通过控制某些物理量的变化,使物体的状态发生缓慢改变,“缓慢”指物体的速度很小,可认为速度为零,所以在变化程中可认为物体处于平衡状态,把物体的这种状态称为动态平衡态。
三、动态平衡
F4
【例题5】如果悬绳AO与竖直方向的夹角θ 减小,BO仍保持水平,重物仍然静止悬挂,悬绳AO和水平绳BO 所受的拉力将分别如何变化?
F3
F1
F2
θ 减小,cosθ 增大,tanθ 减小
减小
减小
三、动态平衡
方法一
:解析法
解析法应用一般步骤:
(1)选某一状态对物体进行受力分析;
(2)将其中两力合成,合力与第三个力等大反向;
(3)列平衡方程求出未知量与已知量的关系表达式;
(4)根据已知量的变化情况来确定未知量的变化情况。
解析法适用于有特殊三角形的时候(直角始终存在)。
是否可以用其他方法解决问题?
三、动态平衡
F3
F1
F2
F4
F3
F1
F2
A′
θ
F4
F3
F1
F2
A′
θ
F4
F1′
F2′
夹角θ 减小,悬绳AO和水平绳BO 所受的拉力都减小。
A
θ =0
F3
F1
F3
F1
F2
F4
方法二
:图解法
图解法适用于三力动态平衡:一力大小方向均不变、一力方向不变、一力大小方向都变。
1.确定恒力、定向力、第三力
2.画出恒力,从恒力末端画出与定向力同方向的虚线,将第三力平移与恒力、定向力构成矢量三角形。
3.根据题中变化条件,比较这些不同形状的矢量三角形,判断各力的大小及变化。
图解法应用一般步骤:
三、动态平衡
【例题6】如图所示,质量均可忽略的轻绳与轻杆承受弹力的最大值一定,杆的A端用铰链固定,光滑轻小滑轮在A点正上方,B端吊一重物,现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前(均未断),关于绳子的拉力F和杆受的弹力N的变化,判断正确的是( )
A.F变大 B.F变小
C.N变大 D.N变小
三、动态平衡
相似三角形法
Tg=G
N
F
T=G
TNB ∽ OBA
N
AB
F
OB
T
OA
=
=
三、动态平衡
【正确答案】B
相似三角形法:物体在三个共点力作用下处于平衡状态时,根据合力为零,把三个力画在一个三角形中,看力的三角形与哪个三角形相似,找到力的三角形与空间三角形相似后,根据相似三角形的对应边成比例,列方程求解.
相似三角形法适用于:有一恒力,另外两个力大小、方向都变。
三、动态平衡
【解析】方法一:解析法
整个装置顺时针转过一个角度后,小球受力如图所示,设AC绳与竖直方向夹角为α,则由平衡条件,有
FT1cosα+FT2cos(θ-α)-mg=0
FT1sinα-FT2sin(θ-α)=0
联立,解得
α从90°逐渐减小为0°,则由上式可知FT1先变大后变小;FT2一直变小,当α=0°时,FT2=0。
【答案】BD
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
三、动态平衡
--
【解析】方法二:正弦定理
整个装置顺时针缓慢转动90°的过程中θ角和mg保持不变,β角从90°减小到0,α角从30°增大到120°,易知FT1先变大后变小;FT2一直变小,当β=0°时,由图易知FT2=0。
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
【答案】BD
--
【解析】方法三:辅助圆
如图,力的三角形的外接圆正好是以初态时的FT2为直径的圆,FT1先变大到最大为圆周直径,然后变小,FT2一直变小,直到0。
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
【答案】BD
辅助圆法:
适用于物体受三个力处于动态平衡时,其中一个力大小、方向均确定,另两个力大小、方向均不确定,但是这两个力的方向夹角保持不变。
方法点拨
课堂小结
平衡状态:物体处于静止或者匀速直线运动的状态。
平衡状态
共点力平衡
动态平衡
F合 = 0
Fx = 0
Fy = 0
F3
F1
F2
F4
正交分解法
第三章 相互作用——力
专题 受力分析
把指定物体(研究对象)在特定的物理环境中受到的所有外力都找出来,并画出受力示意图的过程。
一、受力分析
一、明确研究对象:即明确分析哪个物体的受力情况。
二、按顺序分析物体所受的力:
一重 、二弹、 三摩擦 、四其他
A
三、正确画出物体受力示意图:不要求严格按照要求 画出每个力的大小,但是方向必须准确。
四、检查:防止错画力、多画力、漏画力。
二、受力分析的一般步骤
一、只分析研究对象所受的力,不分析研究对象对其他物体所施的力。
二、只分析根据性质命名的力:重力、弹力、摩擦力、分子力、电磁力、核力。
三、合力与分力不能同时分析。
三、受力分析注意事项
1、单个物体(可看作质点)静止在水平面
地面光滑
四、实例分析
A
向右匀速
(地面光滑)
A
向右运动
(地面粗糙)
A
向右运动
(墙面粗糙)
F>G
2、单个物体(可看作质点)在水平面上运动
四、实例分析
A
A
斜面光滑
3、单个物体(可看作质点)静止在斜面上①
四、实例分析
A
各接触面均光滑
A
各接触面均光滑
3、单个物体(可看作质点)静止在斜面上②
四、实例分析
做一做:木块静止在斜面上,分析斜面的受力情况。
M
m
Gm
FN
Ff
GM
FN′
FN1
Ff ′
A
接触面不光滑
A
接触面不光滑
4、单个物体(可看作质点)在斜面上运动
四、实例分析
1. 水平传送带
2. 倾斜传送带
A
物体随水平传送带一起匀速向右运动
A
物体随倾斜传送带一起匀速斜向上运动
3. 倾斜传送带
A
物体随倾斜传送带一起匀速斜向下运动
5、单个物体(可看作质点)在传送带上
四、实例分析
A
A
墙壁光滑
墙壁粗糙
墙壁光滑
6、单个物体(可看作质点)静止在竖直面上
四、实例分析
A
A
A
A沿竖直墙面下滑
向上爬竿的运动员(无需画出弹力)
7、单个物体(可看作质点)在竖直面上运动
四、实例分析
墙壁光滑,地面粗糙
墙壁光滑,地面粗糙
8、单个物体(非质点问题)静止①
四、实例分析
半球光滑,地面粗糙
杆静止在光滑碗中
8、单个物体(非质点问题)静止②
四、实例分析
8、单个物体(非质点问题)静止③
四、实例分析
OA、OB、AB是三根轻绳,它们构成一个正三角形,装置静止在下图所示的位置,此时OA竖直.画出A、B两球的受力示意图
挑战一下:
G
FA
G
FB
对多个物体的受力情况你会处理吗?
问题1:分别画出A、B、C的三个物体所受的力。
A
B
C
A
对于物体A:
FA
GA
B
对于物体B:
FB
GB
C
对于物体C:
FC
GC
FA ′
FB ′
不要把作用在其它物体上的力错误的认为通过“力的传递”作用在研究对象上。
问题2:在水平桌面上叠放着木块P和Q,水平力F推动两个木块做匀速直线运动,则P和Q的受力情况。
V
P
Q
F
P
GP
F1
Q
f
GQ
F1 ′
F
F2
对多个物体的受力情况有没有更好的处理方法呢?
整体法:就是将几个物体视为一个整体来进行分析的方法。
五、整体法和隔离法
隔离法:将研究对象从周围其他物体中分离出来,单独进行分析的方法。
情景1:
A
B
A、B一起匀速向右运动
A
B
A
B
隔离法
整体法
A
B
A、B一起匀速向右运动
A
B
A
B
情景2:
A
B
C
地面粗糙,计算地面产生的摩擦力
情景3:
A
B
A
B
A
B
情景4:
A
B
A、B静止
滑轮
情景5:
A
B
A、B静止
A
B
A
B
情景6:
C
A
B
情景7:
A
C
B
A
轻绳
轻杆
静止,分析结点A的受力
A
静止,分析结点A的受力
铰链连接
情景8:
A、B静止
A
B
A
B
A
B
情景9:
A、B静止
B
A
A
B
B
A
情景10:
(1)当求整体内部各个物体之间的相互作用力时,优先考虑采用隔离法。
(2)对于多物体问题,如果不求物体间的相互作用力,我们优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便。
两种方法的选用原则:
五、整体法和隔离法
连接体问题的分析,关键是受力分析研究对象的选取
分析:
1.若绳子的拉力为零
2.若绳子有拉力
答案:ACD
总结:(1)分析弹力时,并不一定有接触就一定有弹力,有接触且发生弹性形变才能有弹力.
(2)有面接触产生弹力的位置,也不一定有摩擦力
斜面光滑
第三章 相互作用——力
第五节 共点力的平衡
数学知识的普及
下面四种情况的物体的受力有何特点?
思考:以上四种情况中物体均处于什么状态?
几个力的作用线交于一点
几个力作用于同一点
课堂引入
平衡状态
G
FN
一、平衡状态
二力平衡时两个力:
大小相等,方向相反
G
FN
平衡状态:物体处于静止或者匀速直线运动的状态。
G
F1
F2
G
N
f
当物体受到多个力作用平衡时,它们的受力有何特点
F
f
N
G
合力等于零,即F合=0
一、平衡状态
平衡状态的运动学特征:v=0 或v不变,即:a=0
注意:保持静止和瞬时速度为0意义不同
平衡条件
共点力合力为0的具体表达形式
F合 = 0
物体受三个力:
三个力首尾相接构成一个闭合三角形
任意两个力的合力和第三个力是一对平衡力
正交分解:
Fx = 0
Fy = 0
物体受多个力时:
正交分解:
Fx = 0
Fy = 0
物体受两个力时:
一、平衡状态
可以举些例子吗?
【例题1】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
模型构建
G
Ff
A
B
C
FN
受力分析
二、共点力平衡实例分析
A
B
C
方法一:正交分解法
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图:
沿平行和垂直于斜面两个方向建立直角坐标系,把重力G沿两个坐标轴方向分解为F1和F2。三力平衡转化为四力平衡。
G
FN
Ff
θ
θ
x
y
F1
F2
二、共点力平衡实例分析
以滑梯上正匀速下滑的小孩为研究对象,受力分析如图所示,
支持力和摩擦力的合力与重力等值反向
方法二:合成法
二、共点力平衡实例分析
FN
G
G’
Ff
A
B
C
θ
θ
Ff=μFN
解得 tanθ =μ
可得:h=μ·AC=0.4×6m=2.4m
G
Ff
FN
合成法:把物体所受的力合成为两个力,则这两个力大小相等、方向相反,并且在同一条直线上。
正交分解法:把物体所受的力在两个互相垂直的方向上分解,每个方向上合力都为0。
两种方法的特点:
二、共点力平衡实例分析
模型演示
1.确定研究对象;
2.对研究对象进行受力分析;
3.根据共点力的平衡条件列方程;
4.求解平衡方程;
5.讨论解的合理性和实际意义。
共点力平衡问题的解题步骤
二、共点力平衡实例分析
【例题2】如图悬吊重物的细绳,其 O 点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
F3
F2
F1
二、共点力平衡实例分析
合成法
F3
F2
F1
F5
F3
F2
F1
F6
乙
丙
F3
F1
F2
F4
甲
对于三力平衡问题,可以选择任意的两个力进行合成。对甲:
正交分解法:如图,以O为原点建立直角坐标系。F2方向为x轴正方向,向上为y轴正方向。F1在两坐标轴方向的分矢量分别为F1x 和F1y 。因x、y两方向的合力都等于0,可列方程:
F2 - F1x =0
F1y - F3 =0
即 F2 - F1sinθ=0 (1)
F1cosθ-G =0 (2)
由(1)(2)式解得 F1=G/cosθ,F2=Gtanθ。
即绳AO和绳BO所受的拉力大小分别为Gcosθ和G tanθ。
F3
F1
F2
x
y
F1y
F1x
二、共点力平衡实例分析
【例题3】如图示,BO为一轻杆,AO和CO为两段细绳,重物质量为m,在图示状态静止,求AO绳的张力.
45°
30°
正交分解法
T=G
N
F
x
y
Nx
Ny
Fx
Fy
受力特点:三个力互相不垂直,且夹角(方向)已知。
二、共点力平衡实例分析
受力特点:三个力互相不垂直,且夹角(方向)未知。
【例题4】如图,半径为R的光滑半球的正上方,离球面顶端距离为h的O点,用一根长为l的细线悬挂质量为m的小球,小球靠在半球面上.试求小球对球面压力的大小.
F
N
G
相似三角形法:力的三角形与空间三角形相似
T
二、共点力平衡实例分析
受力特点:三个力互相不垂直,且夹角(方向)未知。
【例题4】如图,半径为R的光滑半球的正上方,离球面顶端距离为h的O点,用一根长为l的细线悬挂质量为m的小球,小球靠在半球面上.试求小球对球面压力的大小.
F
N
G
相似三角形法:力的三角形与空间三角形相似
T
二、共点力平衡实例分析
【例题5】城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂。图为这类结构的一种简化模型。图中硬杆OB可绕通过B点且垂直于纸面的轴转动,钢索和杆的重量都可忽略。如果悬挂物的重量是G,角AOB 等于θ ,钢索AO对O点的拉力和杆OB对O点的支持力各是多大?
二、共点力平衡实例分析
方法一:解析法
水平方向:
竖直方向:
O点受力如图,对O点由共点力平衡条件,
方法2 用正交分解的方法求解。
二、共点力平衡实例分析
方法二:正交分解法
绳子的死结和活结
(1)“活结”:一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的。绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
(2)“死结”:两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。
方法2 用正交分解的方法求解。
二、共点力平衡实例分析
方法2 用正交分解的方法求解。
处理平衡问题的常用方法
动态平衡问题是指通过控制某些物理量的变化,使物体的状态发生缓慢改变,“缓慢”指物体的速度很小,可认为速度为零,所以在变化程中可认为物体处于平衡状态,把物体的这种状态称为动态平衡态。
三、动态平衡
F4
【例题5】如果悬绳AO与竖直方向的夹角θ 减小,BO仍保持水平,重物仍然静止悬挂,悬绳AO和水平绳BO 所受的拉力将分别如何变化?
F3
F1
F2
θ 减小,cosθ 增大,tanθ 减小
减小
减小
三、动态平衡
方法一
:解析法
解析法应用一般步骤:
(1)选某一状态对物体进行受力分析;
(2)将其中两力合成,合力与第三个力等大反向;
(3)列平衡方程求出未知量与已知量的关系表达式;
(4)根据已知量的变化情况来确定未知量的变化情况。
解析法适用于有特殊三角形的时候(直角始终存在)。
是否可以用其他方法解决问题?
三、动态平衡
F3
F1
F2
F4
F3
F1
F2
A′
θ
F4
F3
F1
F2
A′
θ
F4
F1′
F2′
夹角θ 减小,悬绳AO和水平绳BO 所受的拉力都减小。
A
θ =0
F3
F1
F3
F1
F2
F4
方法二
:图解法
图解法适用于三力动态平衡:一力大小方向均不变、一力方向不变、一力大小方向都变。
1.确定恒力、定向力、第三力
2.画出恒力,从恒力末端画出与定向力同方向的虚线,将第三力平移与恒力、定向力构成矢量三角形。
3.根据题中变化条件,比较这些不同形状的矢量三角形,判断各力的大小及变化。
图解法应用一般步骤:
三、动态平衡
【例题6】如图所示,质量均可忽略的轻绳与轻杆承受弹力的最大值一定,杆的A端用铰链固定,光滑轻小滑轮在A点正上方,B端吊一重物,现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前(均未断),关于绳子的拉力F和杆受的弹力N的变化,判断正确的是( )
A.F变大 B.F变小
C.N变大 D.N变小
三、动态平衡
相似三角形法
Tg=G
N
F
T=G
TNB ∽ OBA
N
AB
F
OB
T
OA
=
=
三、动态平衡
【正确答案】B
相似三角形法:物体在三个共点力作用下处于平衡状态时,根据合力为零,把三个力画在一个三角形中,看力的三角形与哪个三角形相似,找到力的三角形与空间三角形相似后,根据相似三角形的对应边成比例,列方程求解.
相似三角形法适用于:有一恒力,另外两个力大小、方向都变。
三、动态平衡
【解析】方法一:解析法
整个装置顺时针转过一个角度后,小球受力如图所示,设AC绳与竖直方向夹角为α,则由平衡条件,有
FT1cosα+FT2cos(θ-α)-mg=0
FT1sinα-FT2sin(θ-α)=0
联立,解得
α从90°逐渐减小为0°,则由上式可知FT1先变大后变小;FT2一直变小,当α=0°时,FT2=0。
【答案】BD
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
三、动态平衡
--
【解析】方法二:正弦定理
整个装置顺时针缓慢转动90°的过程中θ角和mg保持不变,β角从90°减小到0,α角从30°增大到120°,易知FT1先变大后变小;FT2一直变小,当β=0°时,由图易知FT2=0。
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
【答案】BD
--
【解析】方法三:辅助圆
如图,力的三角形的外接圆正好是以初态时的FT2为直径的圆,FT1先变大到最大为圆周直径,然后变小,FT2一直变小,直到0。
【例题7】如图所示,装置中两根细绳拴住一球,保持两细绳间的夹角θ=120°不变,若把整个装置顺时针缓慢转过90°,则在转动过程中,CA绳的拉力FT1,CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
D.FT2一直变小,且最终变为零
【答案】BD
辅助圆法:
适用于物体受三个力处于动态平衡时,其中一个力大小、方向均确定,另两个力大小、方向均不确定,但是这两个力的方向夹角保持不变。
方法点拨
课堂小结
平衡状态:物体处于静止或者匀速直线运动的状态。
平衡状态
共点力平衡
动态平衡
F合 = 0
Fx = 0
Fy = 0
F3
F1
F2
F4
正交分解法
第三章 相互作用——力
专题 受力分析
把指定物体(研究对象)在特定的物理环境中受到的所有外力都找出来,并画出受力示意图的过程。
一、受力分析
一、明确研究对象:即明确分析哪个物体的受力情况。
二、按顺序分析物体所受的力:
一重 、二弹、 三摩擦 、四其他
A
三、正确画出物体受力示意图:不要求严格按照要求 画出每个力的大小,但是方向必须准确。
四、检查:防止错画力、多画力、漏画力。
二、受力分析的一般步骤
一、只分析研究对象所受的力,不分析研究对象对其他物体所施的力。
二、只分析根据性质命名的力:重力、弹力、摩擦力、分子力、电磁力、核力。
三、合力与分力不能同时分析。
三、受力分析注意事项
1、单个物体(可看作质点)静止在水平面
地面光滑
四、实例分析
A
向右匀速
(地面光滑)
A
向右运动
(地面粗糙)
A
向右运动
(墙面粗糙)
F>G
2、单个物体(可看作质点)在水平面上运动
四、实例分析
A
A
斜面光滑
3、单个物体(可看作质点)静止在斜面上①
四、实例分析
A
各接触面均光滑
A
各接触面均光滑
3、单个物体(可看作质点)静止在斜面上②
四、实例分析
做一做:木块静止在斜面上,分析斜面的受力情况。
M
m
Gm
FN
Ff
GM
FN′
FN1
Ff ′
A
接触面不光滑
A
接触面不光滑
4、单个物体(可看作质点)在斜面上运动
四、实例分析
1. 水平传送带
2. 倾斜传送带
A
物体随水平传送带一起匀速向右运动
A
物体随倾斜传送带一起匀速斜向上运动
3. 倾斜传送带
A
物体随倾斜传送带一起匀速斜向下运动
5、单个物体(可看作质点)在传送带上
四、实例分析
A
A
墙壁光滑
墙壁粗糙
墙壁光滑
6、单个物体(可看作质点)静止在竖直面上
四、实例分析
A
A
A
A沿竖直墙面下滑
向上爬竿的运动员(无需画出弹力)
7、单个物体(可看作质点)在竖直面上运动
四、实例分析
墙壁光滑,地面粗糙
墙壁光滑,地面粗糙
8、单个物体(非质点问题)静止①
四、实例分析
半球光滑,地面粗糙
杆静止在光滑碗中
8、单个物体(非质点问题)静止②
四、实例分析
8、单个物体(非质点问题)静止③
四、实例分析
OA、OB、AB是三根轻绳,它们构成一个正三角形,装置静止在下图所示的位置,此时OA竖直.画出A、B两球的受力示意图
挑战一下:
G
FA
G
FB
对多个物体的受力情况你会处理吗?
问题1:分别画出A、B、C的三个物体所受的力。
A
B
C
A
对于物体A:
FA
GA
B
对于物体B:
FB
GB
C
对于物体C:
FC
GC
FA ′
FB ′
不要把作用在其它物体上的力错误的认为通过“力的传递”作用在研究对象上。
问题2:在水平桌面上叠放着木块P和Q,水平力F推动两个木块做匀速直线运动,则P和Q的受力情况。
V
P
Q
F
P
GP
F1
Q
f
GQ
F1 ′
F
F2
对多个物体的受力情况有没有更好的处理方法呢?
整体法:就是将几个物体视为一个整体来进行分析的方法。
五、整体法和隔离法
隔离法:将研究对象从周围其他物体中分离出来,单独进行分析的方法。
情景1:
A
B
A、B一起匀速向右运动
A
B
A
B
隔离法
整体法
A
B
A、B一起匀速向右运动
A
B
A
B
情景2:
A
B
C
地面粗糙,计算地面产生的摩擦力
情景3:
A
B
A
B
A
B
情景4:
A
B
A、B静止
滑轮
情景5:
A
B
A、B静止
A
B
A
B
情景6:
C
A
B
情景7:
A
C
B
A
轻绳
轻杆
静止,分析结点A的受力
A
静止,分析结点A的受力
铰链连接
情景8:
A、B静止
A
B
A
B
A
B
情景9:
A、B静止
B
A
A
B
B
A
情景10:
(1)当求整体内部各个物体之间的相互作用力时,优先考虑采用隔离法。
(2)对于多物体问题,如果不求物体间的相互作用力,我们优先采用整体法,这样涉及的研究对象少,未知量少,方程少,求解简便。
两种方法的选用原则:
五、整体法和隔离法
连接体问题的分析,关键是受力分析研究对象的选取
分析:
1.若绳子的拉力为零
2.若绳子有拉力
答案:ACD
总结:(1)分析弹力时,并不一定有接触就一定有弹力,有接触且发生弹性形变才能有弹力.
(2)有面接触产生弹力的位置,也不一定有摩擦力
斜面光滑
