数学人教A版(2019)选择性必修第三册7.4.2超几何分布 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.4.2超几何分布 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 22:47:54 | ||
图片预览





文档简介
(共21张PPT)
第七章 随机变量及其分布
7.4.2 超几何分布
学习目标
新课程标准解读 核心素养
通过具体实例,理解超几何分布,并能解决简单的实际问题. 逻辑推理、数学运算、数学建模
导
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有
外观相同的10个乒乓球,其中
有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
奖
奖
奖
导
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有外观相同的10个乒乓球,其中有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
如果你是顾客,你选择哪种方案?
方案一:
有放回抽奖两次
方案二:
无放回抽奖两次
解:设X表示抽取10个零件中不合格品数,X的可能取值为0,1,2,3
其分布列为
问题1 一批零件共有30个,其中有3个不合格. 随机抽取10个零件进行检测,求至少有1件不合格的概率.
∴至少有1件不合格的概率为
(直接法)
(间接法)
学
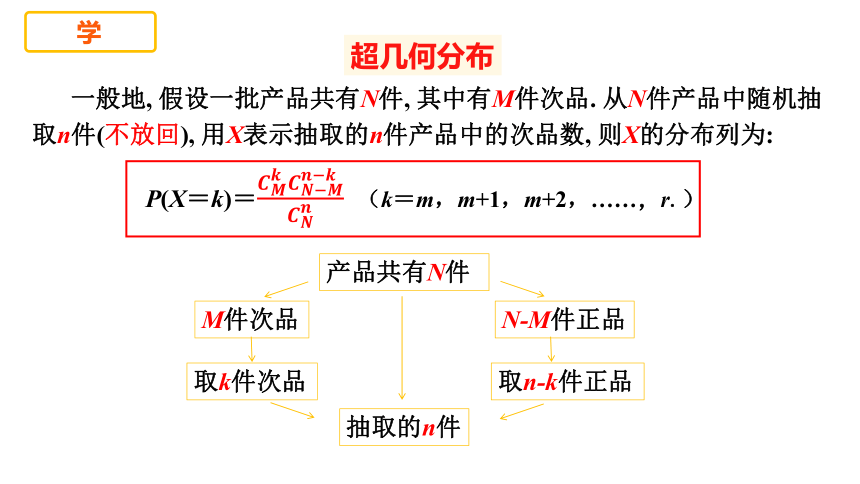
超几何分布
古典概型
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
P(X=k)= (k=m,m+1,m+2,……,r.)
学
产品共有N件
抽取的n件
M件次品
N-M件正品
取k件次品
取n-k件正品
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
其中n, N, M∈N*, M≤N, n≤N, m=max{0, n-(N-M)}, r=min{n, M}. 如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
P(X=k)= (k=m,m+1,m+2,……,r.)
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
问题2:公式中各个字母的含义是什么?
学
①总体是否可分为两类不同的个体;
②不放回地抽取;
③随机变量是否为样本中其中一类个体的数量.
问题3: 怎样判断一个变量是否服从超几何分布?
学
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
P(X=k)= (k=m,m+1,m+2,……,r.)
学
[例1] 下列问题中,哪些属于超几何分布问题,说明理由.
(1)盒子中有红球3只,黄球4只,蓝球5只,任取3只球,把不是红色的球的个数记为X,求X的分布列;
(2)某班级有男生25人,女生20人.选派4名学生参加学校组织的活动,其中女生人数记为X,求X的分布列;
(3)将一枚硬币连抛3次,正面向上的次数X;
(4)某射手射击的命中率为0.8,现对目标射击3次,记命中目标的次数为X.
分两类是红球和不是红球,随机变量X表示抽取n件样本某类样本被抽取的件数,是超几何分布
分两类是红球和不是红球,随机变量X表示抽取n件样本某类样本被抽取的件数,是超几何分布
独立重复试验,X服从二项分布
独立重复试验,X服从二项分布
解:设5名学生中甲被选中为事件A
[例2] 从50 名学生中随机选出5名学生代表,求甲被选中的概率.
因此甲被选中的概率为
学
究
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有外观相同的10个乒乓球,其中有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
如果你是顾客,你选择哪种方案?
方案一:
有放回抽奖两次
方案二:
无放回抽奖两次
究
每个小组分成两个部分,分别进行“有放回抽奖”和“不放回抽奖”,两种方案的计算,再进行小组讨论,给出合理的决策方案.
提示:假设中奖次数为X,奖金为Y,随机变量X的分布列和期望、方差是什么?由此数据你可以给出合理的决策吗?
合作交流
方案二:无放回抽奖两次
究
方案一:有放回抽奖两次
记中奖次数为X,奖金为Y元
X 0 1 2
P
问题6:二项分布、超几何分布有什么区别和联系?
超几何分布 二项分布
试验类型 抽样 抽样
试验种数 有 种物品 有 种结果
总体容量 个 个
随机变量取值的概率 利用 计算 利用 计算
联系 不放回
放回
两
两
有限
无限
古典概型
独立重复试验
(当总体容量很大时)
超几何分布可近似看做二项分布
练
练
练
练
练
(2)请对甲、乙两人进行分析比较,谁获胜的可能性大?
课堂小结
本节课你学到了什么
如何区别二项分布与超几何分布?
课堂小结
具体实例
超几何分布
与二项分布的区别
解决简单的实际问题
P(X=k)=
区别有放回和不放回抽样
利用古典概型计算概率
从特殊到一般
辩模型定取值用公式
第七章 随机变量及其分布
7.4.2 超几何分布
学习目标
新课程标准解读 核心素养
通过具体实例,理解超几何分布,并能解决简单的实际问题. 逻辑推理、数学运算、数学建模
导
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有
外观相同的10个乒乓球,其中
有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
奖
奖
奖
导
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有外观相同的10个乒乓球,其中有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
如果你是顾客,你选择哪种方案?
方案一:
有放回抽奖两次
方案二:
无放回抽奖两次
解:设X表示抽取10个零件中不合格品数,X的可能取值为0,1,2,3
其分布列为
问题1 一批零件共有30个,其中有3个不合格. 随机抽取10个零件进行检测,求至少有1件不合格的概率.
∴至少有1件不合格的概率为
(直接法)
(间接法)
学
超几何分布
古典概型
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
P(X=k)= (k=m,m+1,m+2,……,r.)
学
产品共有N件
抽取的n件
M件次品
N-M件正品
取k件次品
取n-k件正品
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
其中n, N, M∈N*, M≤N, n≤N, m=max{0, n-(N-M)}, r=min{n, M}. 如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
P(X=k)= (k=m,m+1,m+2,……,r.)
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
问题2:公式中各个字母的含义是什么?
学
①总体是否可分为两类不同的个体;
②不放回地抽取;
③随机变量是否为样本中其中一类个体的数量.
问题3: 怎样判断一个变量是否服从超几何分布?
学
一般地, 假设一批产品共有N件, 其中有M件次品. 从N件产品中随机抽取n件(不放回), 用X表示抽取的n件产品中的次品数, 则X的分布列为:
超几何分布
P(X=k)= (k=m,m+1,m+2,……,r.)
学
[例1] 下列问题中,哪些属于超几何分布问题,说明理由.
(1)盒子中有红球3只,黄球4只,蓝球5只,任取3只球,把不是红色的球的个数记为X,求X的分布列;
(2)某班级有男生25人,女生20人.选派4名学生参加学校组织的活动,其中女生人数记为X,求X的分布列;
(3)将一枚硬币连抛3次,正面向上的次数X;
(4)某射手射击的命中率为0.8,现对目标射击3次,记命中目标的次数为X.
分两类是红球和不是红球,随机变量X表示抽取n件样本某类样本被抽取的件数,是超几何分布
分两类是红球和不是红球,随机变量X表示抽取n件样本某类样本被抽取的件数,是超几何分布
独立重复试验,X服从二项分布
独立重复试验,X服从二项分布
解:设5名学生中甲被选中为事件A
[例2] 从50 名学生中随机选出5名学生代表,求甲被选中的概率.
因此甲被选中的概率为
学
究
五一假期即将来临,某商家拟推出一项抽奖优惠活动:在一个不透明的箱子中,放有外观相同的10个乒乓球,其中有3个乒乓球的表面写有“奖”字,顾客消费满500元便可获得两次抽奖机会,每次从箱子中任意摸取一个球,抽中带“奖”字的乒乓球,均可获得100元现金代金券。
如果你是顾客,你选择哪种方案?
方案一:
有放回抽奖两次
方案二:
无放回抽奖两次
究
每个小组分成两个部分,分别进行“有放回抽奖”和“不放回抽奖”,两种方案的计算,再进行小组讨论,给出合理的决策方案.
提示:假设中奖次数为X,奖金为Y,随机变量X的分布列和期望、方差是什么?由此数据你可以给出合理的决策吗?
合作交流
方案二:无放回抽奖两次
究
方案一:有放回抽奖两次
记中奖次数为X,奖金为Y元
X 0 1 2
P
问题6:二项分布、超几何分布有什么区别和联系?
超几何分布 二项分布
试验类型 抽样 抽样
试验种数 有 种物品 有 种结果
总体容量 个 个
随机变量取值的概率 利用 计算 利用 计算
联系 不放回
放回
两
两
有限
无限
古典概型
独立重复试验
(当总体容量很大时)
超几何分布可近似看做二项分布
练
练
练
练
练
(2)请对甲、乙两人进行分析比较,谁获胜的可能性大?
课堂小结
本节课你学到了什么
如何区别二项分布与超几何分布?
课堂小结
具体实例
超几何分布
与二项分布的区别
解决简单的实际问题
P(X=k)=
区别有放回和不放回抽样
利用古典概型计算概率
从特殊到一般
辩模型定取值用公式
