2023-2024学年华东师大版数学九年级下册 26.2.8 求二次函数的表达式课件 (共22张PPT)
文档属性
| 名称 | 2023-2024学年华东师大版数学九年级下册 26.2.8 求二次函数的表达式课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 905.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
26.2 二次函数的图象与性质
课时8 求二次函数的表达式
过基础 教材必备知识精练
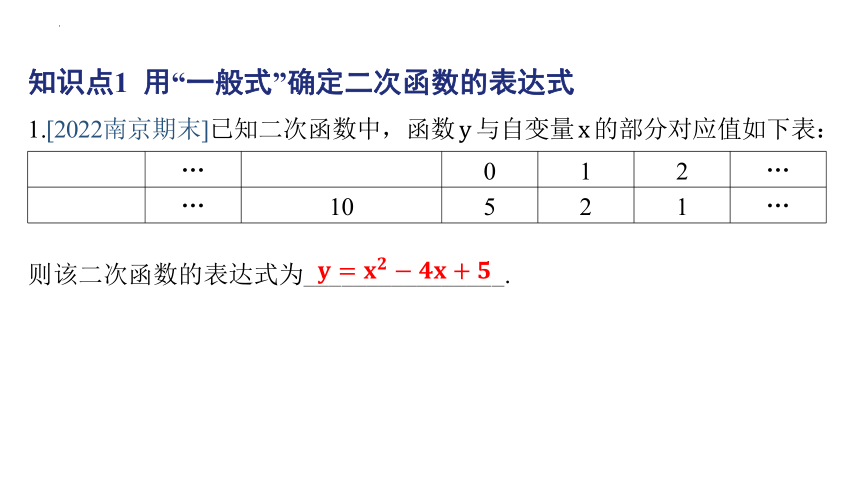
知识点1 用“一般式”确定二次函数的表达式
1.[2022南京期末]已知二次函数中,函数 与自变量 的部分对应值如下表:
… 0 1 2 …
… 10 5 2 1 …
则该二次函数的表达式为_ _______________.
【解析】 设该二次函数的表达式为 .由题表中数
据知,当 时, ,当 时, ,当 时,
, 解得 该二次函数的表达式为
.
2.[2023张家口月考]将抛物线 平移后经过点 , ,求
平移后抛物线的表达式.
解:设平移后抛物线的表达式为 ,
抛物线 经过点 , ,
解得
平移后抛物线的表达式为 .
3.[2022湖州期中]已知抛物线 经过点 , .
(1)求 , 的值;
解:把 , 分别代入 ,
得 解得
(2)若 , 是抛物线上不同的两点,且 ,求
的值.
由(1)得抛物线的表达式为 ,
把 代入 ,得 ,
, .
又 抛物线的对称轴为直线 ,
, .
知识点2 用“顶点式”确定二次函数的表达式
4.若抛物线的顶点在原点,且过点 ,则抛物线对应的函数表达式是
( )
C
A. B. C. D.
【解析】 设该抛物线对应的函数表达式是 .因为抛物线过点
,所以 ,所以 ,所以 .
5.[2023驻马店期中]与抛物线 的形状、开口方向完全相同,且顶
点坐标是 的抛物线的表达式为( )
B
A. B.
C. D.
【解析】 该抛物线的表达式为 .
6.二次函数的图象如图所示,则这个二次函数的表达式
为_ _______________.
【解析】 由题图可知图象的顶点坐标是 ,与
轴负半轴的交点坐标是 ,所以可设二次函数的表
达式为 ,把 代入,得
,解得 ,所以
.
变式 [2023北京昌平区期中]二次函数的部分图象如图
所示,对称轴是直线 ,则这个二次函数的表达
式为_ ________________.
【解析】 由题图知二次函数的图象的对称轴为直线
,且过点 , .设二次函数的表达式
为 ,将 , 分别代入,
得 解得 则这个二次函数的表达
式为 .
知识点3 用“交点式”确定二次函数的表达式
7.如图,已知二次函数 的图象与
轴交于 , 两点,与 轴交于点 ,
则二次函数的图象的顶点坐标是_ _______.
【解析】 设该二次函数的表达式为
,把点 的坐标代入,得
,
, 二次函数的图象的顶点坐标是 .
26.2 二次函数的图象与性质
课时8 求二次函数的表达式
过能力 学科关键能力构建
1.[2022新余一中期中]如图,抛物线 与过点
且平行于 轴的直线相交于点 , ,与 轴交于点 .若 为直角,则该
抛物线的表达式为( )
B
A.
B.
C.
D.
【解析】 如图,设直线 与 轴交于点 ,则
, .根据抛物线的对称性及直
线 过点 且平行于 轴,得 为等腰三角
形, , 为等腰直角三角形,
, .把 代入 ,得
,解得 , 该抛物线的表达式为 .
2.[2023长春模拟]在“探索函数 的系数
, , 与图象的关系”活动中,老师给出了平面直角坐标
系中的四个点: , , , ,如图.同
学们探索了经过这四个点中的三个点的二次函数的图
A
A. B. C. D.
象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
【解析】 抛物线经过的三点有四种情况,分别为: , , ; ,
, ; , , ; , , .通过描大致图象可知,当抛物线经过
点 , , 或 , , 时, ;当抛物线经过点 , , 或 ,
, 时, .①抛物线经过点 , , 时,易知 .将点 , 的
坐标分别代入 ,可求得 ②抛物线经过点 , ,
时,易知 ,将点 , 的坐标分别代入 ,可求
得 .故 的值最大为 .
3.[2023朔州朔城区期中]在平面直角坐标系中,抛物线 与
轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为
( )
A
A. B.
C. D.
【解析】 抛物线 的顶点坐标是 ,
点 的坐标为 ,所以与该抛物线关于点 成中心对称的抛物线的顶
点坐标是 ,且开口向下,所以与该抛物线关于点 成中心对称的
抛物线的表达式为 .
4.新趋势·结论开放[2022沈阳模拟]如果抛物线 的顶点在抛物线 上,
抛物线 的顶点也在抛物线 上,此时我们称抛物线 与 是“互为关
联”的抛物线.那么与抛物线 是“互为关联”且顶点不同的抛物线的
函数表达式可以是_ ________________________________.(写出一个即可)
(答案不唯一)
【解析】 抛物线 的顶点坐标为 ,设与其“互为关联”抛物线
的函数表达式为 ,把 的坐标代入,得 ,
所以与抛物线 是“互为关联”的抛物线的函数表达式为
.当 时, .
5.[2022黔东南州中考]在平面直角坐标系中,将抛物线 先
绕原点旋转 ,再向下平移5个单位,所得到的抛物线的顶点坐标是
_ _______.
【解析】 将抛物线 绕原点旋转 后,所得的抛物线
为 ,整理后为 将抛物线
向下平移5个单位,得抛物线
,所以所得到的抛物线的顶点坐标
是 .
6.[2023绍兴中考]已知二次函数 .
(1)当 , 时,
①求该函数图象的顶点坐标;
解:当 , 时, ,
该函数图象的顶点坐标为 .
②当 时,求 的取值范围.
中含有顶点的横坐标2,
当 时, 有最大值7.
,
当 时, 有最小值 .
当 时, .
(2)当 时, 的最大值为2;当 时, 的最大值为3.求二次函
数的表达式.
由题意,得抛物线的对称轴直线 在 轴的右侧, .
抛物线开口向下,当 时, 的最大值为2, .
, .
, , .
26.2 二次函数的图象与性质
课时8 求二次函数的表达式
过基础 教材必备知识精练
知识点1 用“一般式”确定二次函数的表达式
1.[2022南京期末]已知二次函数中,函数 与自变量 的部分对应值如下表:
… 0 1 2 …
… 10 5 2 1 …
则该二次函数的表达式为_ _______________.
【解析】 设该二次函数的表达式为 .由题表中数
据知,当 时, ,当 时, ,当 时,
, 解得 该二次函数的表达式为
.
2.[2023张家口月考]将抛物线 平移后经过点 , ,求
平移后抛物线的表达式.
解:设平移后抛物线的表达式为 ,
抛物线 经过点 , ,
解得
平移后抛物线的表达式为 .
3.[2022湖州期中]已知抛物线 经过点 , .
(1)求 , 的值;
解:把 , 分别代入 ,
得 解得
(2)若 , 是抛物线上不同的两点,且 ,求
的值.
由(1)得抛物线的表达式为 ,
把 代入 ,得 ,
, .
又 抛物线的对称轴为直线 ,
, .
知识点2 用“顶点式”确定二次函数的表达式
4.若抛物线的顶点在原点,且过点 ,则抛物线对应的函数表达式是
( )
C
A. B. C. D.
【解析】 设该抛物线对应的函数表达式是 .因为抛物线过点
,所以 ,所以 ,所以 .
5.[2023驻马店期中]与抛物线 的形状、开口方向完全相同,且顶
点坐标是 的抛物线的表达式为( )
B
A. B.
C. D.
【解析】 该抛物线的表达式为 .
6.二次函数的图象如图所示,则这个二次函数的表达式
为_ _______________.
【解析】 由题图可知图象的顶点坐标是 ,与
轴负半轴的交点坐标是 ,所以可设二次函数的表
达式为 ,把 代入,得
,解得 ,所以
.
变式 [2023北京昌平区期中]二次函数的部分图象如图
所示,对称轴是直线 ,则这个二次函数的表达
式为_ ________________.
【解析】 由题图知二次函数的图象的对称轴为直线
,且过点 , .设二次函数的表达式
为 ,将 , 分别代入,
得 解得 则这个二次函数的表达
式为 .
知识点3 用“交点式”确定二次函数的表达式
7.如图,已知二次函数 的图象与
轴交于 , 两点,与 轴交于点 ,
则二次函数的图象的顶点坐标是_ _______.
【解析】 设该二次函数的表达式为
,把点 的坐标代入,得
,
, 二次函数的图象的顶点坐标是 .
26.2 二次函数的图象与性质
课时8 求二次函数的表达式
过能力 学科关键能力构建
1.[2022新余一中期中]如图,抛物线 与过点
且平行于 轴的直线相交于点 , ,与 轴交于点 .若 为直角,则该
抛物线的表达式为( )
B
A.
B.
C.
D.
【解析】 如图,设直线 与 轴交于点 ,则
, .根据抛物线的对称性及直
线 过点 且平行于 轴,得 为等腰三角
形, , 为等腰直角三角形,
, .把 代入 ,得
,解得 , 该抛物线的表达式为 .
2.[2023长春模拟]在“探索函数 的系数
, , 与图象的关系”活动中,老师给出了平面直角坐标
系中的四个点: , , , ,如图.同
学们探索了经过这四个点中的三个点的二次函数的图
A
A. B. C. D.
象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
【解析】 抛物线经过的三点有四种情况,分别为: , , ; ,
, ; , , ; , , .通过描大致图象可知,当抛物线经过
点 , , 或 , , 时, ;当抛物线经过点 , , 或 ,
, 时, .①抛物线经过点 , , 时,易知 .将点 , 的
坐标分别代入 ,可求得 ②抛物线经过点 , ,
时,易知 ,将点 , 的坐标分别代入 ,可求
得 .故 的值最大为 .
3.[2023朔州朔城区期中]在平面直角坐标系中,抛物线 与
轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为
( )
A
A. B.
C. D.
【解析】 抛物线 的顶点坐标是 ,
点 的坐标为 ,所以与该抛物线关于点 成中心对称的抛物线的顶
点坐标是 ,且开口向下,所以与该抛物线关于点 成中心对称的
抛物线的表达式为 .
4.新趋势·结论开放[2022沈阳模拟]如果抛物线 的顶点在抛物线 上,
抛物线 的顶点也在抛物线 上,此时我们称抛物线 与 是“互为关
联”的抛物线.那么与抛物线 是“互为关联”且顶点不同的抛物线的
函数表达式可以是_ ________________________________.(写出一个即可)
(答案不唯一)
【解析】 抛物线 的顶点坐标为 ,设与其“互为关联”抛物线
的函数表达式为 ,把 的坐标代入,得 ,
所以与抛物线 是“互为关联”的抛物线的函数表达式为
.当 时, .
5.[2022黔东南州中考]在平面直角坐标系中,将抛物线 先
绕原点旋转 ,再向下平移5个单位,所得到的抛物线的顶点坐标是
_ _______.
【解析】 将抛物线 绕原点旋转 后,所得的抛物线
为 ,整理后为 将抛物线
向下平移5个单位,得抛物线
,所以所得到的抛物线的顶点坐标
是 .
6.[2023绍兴中考]已知二次函数 .
(1)当 , 时,
①求该函数图象的顶点坐标;
解:当 , 时, ,
该函数图象的顶点坐标为 .
②当 时,求 的取值范围.
中含有顶点的横坐标2,
当 时, 有最大值7.
,
当 时, 有最小值 .
当 时, .
(2)当 时, 的最大值为2;当 时, 的最大值为3.求二次函
数的表达式.
由题意,得抛物线的对称轴直线 在 轴的右侧, .
抛物线开口向下,当 时, 的最大值为2, .
, .
, , .
