2023-2024学年华东师大版数学九年级下册 26.2.4 二次函数y=a(x-h)^2 k的图象与性质课件-(共24张PPT)
文档属性
| 名称 | 2023-2024学年华东师大版数学九年级下册 26.2.4 二次函数y=a(x-h)^2 k的图象与性质课件-(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 955.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 10:08:17 | ||
图片预览








文档简介
(共24张PPT)
26.2 二次函数的图象与性质
课时4 二次函数y=图象与性质
过基础 教材必备知识精练
知识点1 二次函数 与 的图象之间的
关系
1.[2023广西中考]将抛物线 先向右平移3个单位,再向上平移4个单
位,得到的抛物线是( )
A
A. B.
C. D.
【方法指导】
平移的规律:“上加下减”常数项,“左加右减”自变量.
知识点2 二次函数 的图象与性质
2.把二次函数 的图象向右平移1个单位,平移后图象的函数
关系式为( )
C
A. B.
C. D.
3.[2022郴州中考]关于二次函数 ,下列说法正确的是
( )
D
A.函数图象的开口向下
B.函数图象的顶点坐标是
C.该函数有最大值,最大值是5
D.当 时, 随 的增大而增大
【解析】 二次函数 的图象开口向上,顶点坐标是 ,
故A,B错误;函数图象的开口向上,该函数有最小值5,故C错误;函数
图象的对称轴为直线 ,当 时, 随 的增大而减小,当
时, 随 的增大而增大,故D正确.
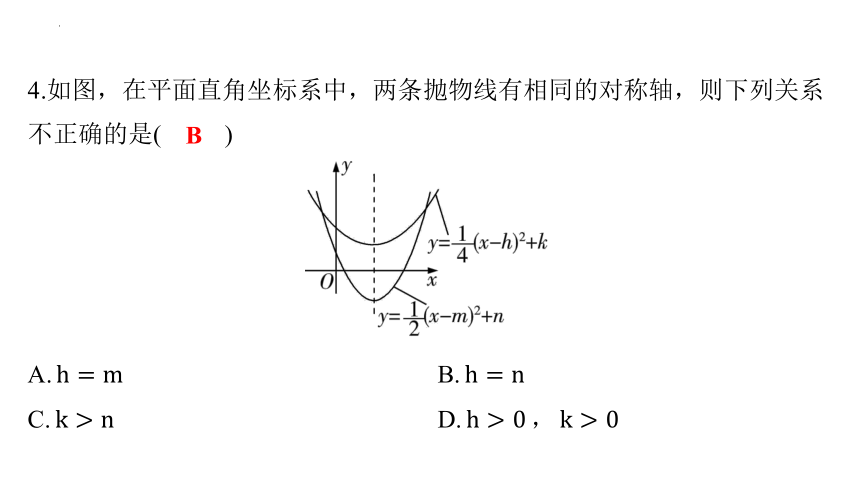
4.如图,在平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系
不正确的是( )
B
A. B.
C. D. ,
【解析】 由题中图象,可知 , ,故D中的关系正确;因为两条抛物线有相同的对称轴,所以 ,故A中的关系正确;由 , , ,得 , ,故B中的关系不正确,C中的关系正确.
5.设 , , 是抛物线 上的三
点,则 , , 的大小关系为_ ____________.(用“ ”连接)
【解析】 抛物线 的开口向下,对称轴为直线 ,点 关于直线 的对称点的坐标为 ,当 时, 随 的增大而增大,因为 ,所以 .
6.教材P16练习T3变式 已知抛物线 .
(1)请你直接写出该抛物线的顶点坐标和对称轴;
解:抛物线 的顶点坐标是 ,对称轴是直线 .
(2)请你在所给平面直角坐标系(如图1)中画出该抛物线上满足
的一段.
经过 , , 三点画抛物线上满足 的一段
如图2所示.
图1 图2
26.2 二次函数的图象与性质
课时4 二次函数y=图象与性质
过能力 学科关键能力构建
1.教材P16练习T2变式 [2023泰安模拟]抛物线的函数关系式为
,若将 轴向上平移2个单位,将 轴向左平移3个单位,
则该抛物线在新的平面直角坐标系中的函数关系式为( )
C
A. B.
C. D.
【解析】 将 轴向上平移2个单位,将 轴向左平移3个单位,相当于将
抛物线 向下平移2个单位,再向右平移3个单位,故抛
物线在新的平面直角坐标系中的函数关系式为 ,
即 .
2.[2022温州中考]已知点 , , 都在抛物线
上,点 在点 左侧,下列选项正确的是( )
D
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【解析】 抛物线 的对称轴为直线 ,且开口向
上, 当 时, 随 的增大而增大,当 时, 随 的增大而
减小. 点 , 都在抛物线 上,点 在点
左侧, , .若 , , , ,故
选项A,B都不符合题意.若 , , , ,
故选项C不符合题意,选项D符合题意.
3.[2023济南二模]已知抛物线 与 轴有两个交点
, ,抛物线 与 轴的一个交点是
,则 的值是( )
C
A.5 B. C.5或1 D. 或
【解析】 抛物线 的对称轴为直线 ,抛物线
的对称轴为直线 , 当点 平
移后的对应点为 时, ;当点 平移后的对应
点为 时, .综上可得, 的值为5或1.
4.已知二次函数 为常数),当
取不同的值时,其图象构成一个“抛物线系”.如图是当
取四个不同数值时此二次函数的图象,发现它们的顶
点在同一条直线上,那么这条直线的关系式是________
_______.
【解析】 抛物线 的顶点坐标为
,设 ①, ,
① ,得 ,即 ,故这条
直线的关系式是 .
5.已知二次函数 的图象如图所示.
(1)请在同一平面直角坐标系中画出二次函数 的图象;
解:二次函数 的图象如图所示:
(2)平行于 轴的直线 在抛物线 上截得线段
(点 在点 的左边),求抛物线 的顶点到线
段 的距离;
已知线段 ,
易知点 和点 关于直线 对称,
所以点 和点 的横坐标分别为0,4.
将 代入 ,得 ,所以 .
因为抛物线 的顶点坐标为 ,
所以抛物线 的顶点到线段 的距离为 .
(3)当 时,利用函数图象比较 与 的大小.
当 时, ;
当 时, ;
当 时, .
素养提升
6.运算能力[2023湖州期中]如图,已知点 , 在二次函
数 的图象上,且 .
(1)若 , ,求顶点到 的距离.
解: ,
二次函数的表达式为 ,顶点坐标为 .
, 点 , 关于抛物线的对称轴对称.
抛物线的对称轴是直线 ,且 ,
, .
当 时, ,
当 时,顶点到 的距离为 .
(2)当 时,二次函数的最大值与最小值的差为1,点 ,
在对称轴的异侧,求 的取值范围.
已知点 , 在对称轴的异侧,对称轴为直线 .
若 ,则 ,且 .
, .
函数的最大值为 ,最小值为 ,
, .
, .
若 ,则 ,且 .
, .
函数的最大值为 ,最小值为 ,
, .
, .
综上所述, 的取值范围为 .
26.2 二次函数的图象与性质
课时4 二次函数y=图象与性质
过基础 教材必备知识精练
知识点1 二次函数 与 的图象之间的
关系
1.[2023广西中考]将抛物线 先向右平移3个单位,再向上平移4个单
位,得到的抛物线是( )
A
A. B.
C. D.
【方法指导】
平移的规律:“上加下减”常数项,“左加右减”自变量.
知识点2 二次函数 的图象与性质
2.把二次函数 的图象向右平移1个单位,平移后图象的函数
关系式为( )
C
A. B.
C. D.
3.[2022郴州中考]关于二次函数 ,下列说法正确的是
( )
D
A.函数图象的开口向下
B.函数图象的顶点坐标是
C.该函数有最大值,最大值是5
D.当 时, 随 的增大而增大
【解析】 二次函数 的图象开口向上,顶点坐标是 ,
故A,B错误;函数图象的开口向上,该函数有最小值5,故C错误;函数
图象的对称轴为直线 ,当 时, 随 的增大而减小,当
时, 随 的增大而增大,故D正确.
4.如图,在平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系
不正确的是( )
B
A. B.
C. D. ,
【解析】 由题中图象,可知 , ,故D中的关系正确;因为两条抛物线有相同的对称轴,所以 ,故A中的关系正确;由 , , ,得 , ,故B中的关系不正确,C中的关系正确.
5.设 , , 是抛物线 上的三
点,则 , , 的大小关系为_ ____________.(用“ ”连接)
【解析】 抛物线 的开口向下,对称轴为直线 ,点 关于直线 的对称点的坐标为 ,当 时, 随 的增大而增大,因为 ,所以 .
6.教材P16练习T3变式 已知抛物线 .
(1)请你直接写出该抛物线的顶点坐标和对称轴;
解:抛物线 的顶点坐标是 ,对称轴是直线 .
(2)请你在所给平面直角坐标系(如图1)中画出该抛物线上满足
的一段.
经过 , , 三点画抛物线上满足 的一段
如图2所示.
图1 图2
26.2 二次函数的图象与性质
课时4 二次函数y=图象与性质
过能力 学科关键能力构建
1.教材P16练习T2变式 [2023泰安模拟]抛物线的函数关系式为
,若将 轴向上平移2个单位,将 轴向左平移3个单位,
则该抛物线在新的平面直角坐标系中的函数关系式为( )
C
A. B.
C. D.
【解析】 将 轴向上平移2个单位,将 轴向左平移3个单位,相当于将
抛物线 向下平移2个单位,再向右平移3个单位,故抛
物线在新的平面直角坐标系中的函数关系式为 ,
即 .
2.[2022温州中考]已知点 , , 都在抛物线
上,点 在点 左侧,下列选项正确的是( )
D
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【解析】 抛物线 的对称轴为直线 ,且开口向
上, 当 时, 随 的增大而增大,当 时, 随 的增大而
减小. 点 , 都在抛物线 上,点 在点
左侧, , .若 , , , ,故
选项A,B都不符合题意.若 , , , ,
故选项C不符合题意,选项D符合题意.
3.[2023济南二模]已知抛物线 与 轴有两个交点
, ,抛物线 与 轴的一个交点是
,则 的值是( )
C
A.5 B. C.5或1 D. 或
【解析】 抛物线 的对称轴为直线 ,抛物线
的对称轴为直线 , 当点 平
移后的对应点为 时, ;当点 平移后的对应
点为 时, .综上可得, 的值为5或1.
4.已知二次函数 为常数),当
取不同的值时,其图象构成一个“抛物线系”.如图是当
取四个不同数值时此二次函数的图象,发现它们的顶
点在同一条直线上,那么这条直线的关系式是________
_______.
【解析】 抛物线 的顶点坐标为
,设 ①, ,
① ,得 ,即 ,故这条
直线的关系式是 .
5.已知二次函数 的图象如图所示.
(1)请在同一平面直角坐标系中画出二次函数 的图象;
解:二次函数 的图象如图所示:
(2)平行于 轴的直线 在抛物线 上截得线段
(点 在点 的左边),求抛物线 的顶点到线
段 的距离;
已知线段 ,
易知点 和点 关于直线 对称,
所以点 和点 的横坐标分别为0,4.
将 代入 ,得 ,所以 .
因为抛物线 的顶点坐标为 ,
所以抛物线 的顶点到线段 的距离为 .
(3)当 时,利用函数图象比较 与 的大小.
当 时, ;
当 时, ;
当 时, .
素养提升
6.运算能力[2023湖州期中]如图,已知点 , 在二次函
数 的图象上,且 .
(1)若 , ,求顶点到 的距离.
解: ,
二次函数的表达式为 ,顶点坐标为 .
, 点 , 关于抛物线的对称轴对称.
抛物线的对称轴是直线 ,且 ,
, .
当 时, ,
当 时,顶点到 的距离为 .
(2)当 时,二次函数的最大值与最小值的差为1,点 ,
在对称轴的异侧,求 的取值范围.
已知点 , 在对称轴的异侧,对称轴为直线 .
若 ,则 ,且 .
, .
函数的最大值为 ,最小值为 ,
, .
, .
若 ,则 ,且 .
, .
函数的最大值为 ,最小值为 ,
, .
, .
综上所述, 的取值范围为 .
