2023-2024学年华东师大版数学九年级下册第26章 二次函数专项3 利用二次函数解决几何中的最值问题课件-(共25张PPT)
文档属性
| 名称 | 2023-2024学年华东师大版数学九年级下册第26章 二次函数专项3 利用二次函数解决几何中的最值问题课件-(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 913.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 10:10:19 | ||
图片预览







文档简介
(共25张PPT)
第26章 二次函数
专项3 利用二次函数解决几何中的最值问题
过专项 阶段强化专项训练
类型1 线段(周长)的最值问题
【方法指导】
常见构造二次函数关系求线段的最值问题
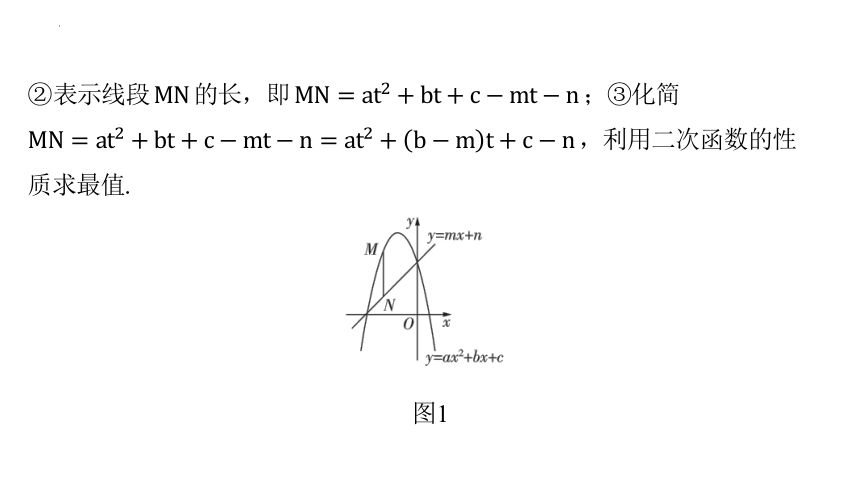
1.求竖直线段 长度最值的步骤(如图1,点 在点 上方):①设点 ,则 ;
②表示线段 的长,即 ;③化简
,利用二次函数的性
质求最值.
图1
2.求斜线段 长度最值的步骤(如图2):①设点 ,
;②用式子表示出 ,即
;③化简 ,利用二次函
数的性质求最值.
图2
图1
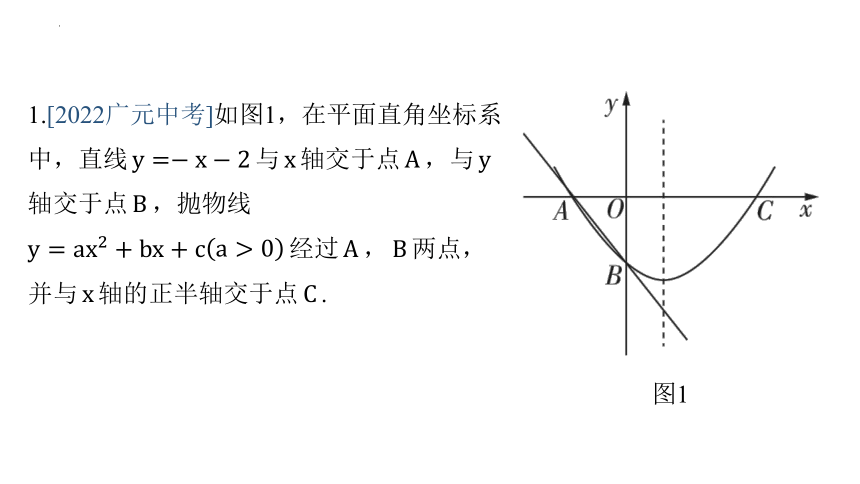
1.[2022广元中考]如图1,在平面直角坐标系
中,直线 与 轴交于点 ,与
轴交于点 ,抛物线
经过 , 两点,
并与 轴的正半轴交于点 .
(1)求 , 满足的关系式及 的值;
解:已知直线 ,
当 时, , ,
当 时, , , .
将 , 的坐标分别代入 ,
得 , , .
(2)当 时,若点 是抛物线对称轴上的一个动点,求 周长
的最小值;
图1
当 时, , ,
,
抛物线的表达式为
,
抛物线的对称轴是直线 .
由抛物线的对称性可得 ,
要使 的周长最小,只需 的长度最小即可.
如图1,连接 交直线 于点 ,连接 ,
点 与点 关于直线 对称, ,
,
此时 的周长最小,其周长为 .
在 中, .
在 中, .
周长的最小值为 .
图2
(3)如图2,当 时,若点 是直线 下
方抛物线上的一个动点,过点 作 于
点 ,当 的值最大时,求此时点 的坐标及
的最大值.
图2
当 时, , ,
,
, , ,
, 是等腰直角三角形,
.
如图2,过点 作 轴于点 ,交 于点 ,
则 是等腰直角三角形.
设 ,则 ,
,
.
当 时, 有最大值 .
当 时, .
综上,点 的坐标为 时, 有最大值 .
类型2 面积的最值问题
【方法指导】
1.割补法:解题的关键点为利用割或补的方法,将所求不规则图形的面积转化为规则图形面积的和或差,然后利用规则图形的面积公式求解.
2.平移法:思路的两处关键点为①底定三角形的面积最值由高确定;②平行线间的距离处处相等.解法的两处关键点为①由直线与抛物线只有一个交点得“根的判别式为0”,进而解出交点坐标;②由“平行线间的距离处处相等”将所求三角形的面积转化为一边在 轴或 轴上的三角形的面积,或有一边平行于 轴或 轴的三角形的面积,
如图,将 的面积转化为 的面积(点 为过点 与 平行
的直线与 轴的交点)求解.
2.一题多解[2023珠海期中]如图,在 中,
, , ,点 从
点 出发沿 向点 以 的速度运动,同时
点 从点 出发沿 向点 以 的速度运动
15
(当一个点到达终点时,另一个点也停止运动),在运动过程中,四边
形 的面积的最小值为____ .
【解析】解法一 在 中, , , , .设运动时间为 ,易知 ,则
, , , 当 时,四边形 的面积取得最小值,最小值为
.
解法二 , 当 的面积最大时,四
边形 的面积最小.在 中, , ,
, .设运动时间为 ,易知
,则 , ,
, 当
时, 的面积取得最大值,最大值为 , 四边形
的面积的最小值为 .
3.一题多解如图,已知抛物线经过两点 , ,且其对称轴为
直线 .
(1)求此抛物线的表达式;
解:已知抛物线的对称轴是直线 ,且抛物线经过点 ,
由抛物线的对称性可知,抛物线经过点 .
设抛物线的表达式为 .
把 的坐标代入 ,得 , ,
抛物线的表达式为 .
(2)若点 是抛物线上点 与点 之间的动点(不包括点 、点 ,求
的面积的最大值,并求出此时点 的坐标.
解法一 设直线 的函数表达式为
,
, , 解得
直线 的函数表达式为 .
如图,过点 作 轴于点 ,交直线 于点 .
设 , ,则 .
,
.
当 时, 有最大值,最大值为 ,此时点 的纵坐标为
,
的面积的最大值为 ,此时点 的坐标为 , .
解法二 如图,将直线 平移,使其与抛物线只有
一个交点 ,连接 ,此时 的面积最大.
由解法一知直线 的函数表达式为 ,
可设直线 的表达式为 .
联立,得 ,
即 .
由 ,得 .
由求根公式,得 ,此时 .
.
, , ,
.
的面积的最大值为 ,此时点 的坐标为 .
第26章 二次函数
专项3 利用二次函数解决几何中的最值问题
过专项 阶段强化专项训练
类型1 线段(周长)的最值问题
【方法指导】
常见构造二次函数关系求线段的最值问题
1.求竖直线段 长度最值的步骤(如图1,点 在点 上方):①设点 ,则 ;
②表示线段 的长,即 ;③化简
,利用二次函数的性
质求最值.
图1
2.求斜线段 长度最值的步骤(如图2):①设点 ,
;②用式子表示出 ,即
;③化简 ,利用二次函
数的性质求最值.
图2
图1
1.[2022广元中考]如图1,在平面直角坐标系
中,直线 与 轴交于点 ,与
轴交于点 ,抛物线
经过 , 两点,
并与 轴的正半轴交于点 .
(1)求 , 满足的关系式及 的值;
解:已知直线 ,
当 时, , ,
当 时, , , .
将 , 的坐标分别代入 ,
得 , , .
(2)当 时,若点 是抛物线对称轴上的一个动点,求 周长
的最小值;
图1
当 时, , ,
,
抛物线的表达式为
,
抛物线的对称轴是直线 .
由抛物线的对称性可得 ,
要使 的周长最小,只需 的长度最小即可.
如图1,连接 交直线 于点 ,连接 ,
点 与点 关于直线 对称, ,
,
此时 的周长最小,其周长为 .
在 中, .
在 中, .
周长的最小值为 .
图2
(3)如图2,当 时,若点 是直线 下
方抛物线上的一个动点,过点 作 于
点 ,当 的值最大时,求此时点 的坐标及
的最大值.
图2
当 时, , ,
,
, , ,
, 是等腰直角三角形,
.
如图2,过点 作 轴于点 ,交 于点 ,
则 是等腰直角三角形.
设 ,则 ,
,
.
当 时, 有最大值 .
当 时, .
综上,点 的坐标为 时, 有最大值 .
类型2 面积的最值问题
【方法指导】
1.割补法:解题的关键点为利用割或补的方法,将所求不规则图形的面积转化为规则图形面积的和或差,然后利用规则图形的面积公式求解.
2.平移法:思路的两处关键点为①底定三角形的面积最值由高确定;②平行线间的距离处处相等.解法的两处关键点为①由直线与抛物线只有一个交点得“根的判别式为0”,进而解出交点坐标;②由“平行线间的距离处处相等”将所求三角形的面积转化为一边在 轴或 轴上的三角形的面积,或有一边平行于 轴或 轴的三角形的面积,
如图,将 的面积转化为 的面积(点 为过点 与 平行
的直线与 轴的交点)求解.
2.一题多解[2023珠海期中]如图,在 中,
, , ,点 从
点 出发沿 向点 以 的速度运动,同时
点 从点 出发沿 向点 以 的速度运动
15
(当一个点到达终点时,另一个点也停止运动),在运动过程中,四边
形 的面积的最小值为____ .
【解析】解法一 在 中, , , , .设运动时间为 ,易知 ,则
, , , 当 时,四边形 的面积取得最小值,最小值为
.
解法二 , 当 的面积最大时,四
边形 的面积最小.在 中, , ,
, .设运动时间为 ,易知
,则 , ,
, 当
时, 的面积取得最大值,最大值为 , 四边形
的面积的最小值为 .
3.一题多解如图,已知抛物线经过两点 , ,且其对称轴为
直线 .
(1)求此抛物线的表达式;
解:已知抛物线的对称轴是直线 ,且抛物线经过点 ,
由抛物线的对称性可知,抛物线经过点 .
设抛物线的表达式为 .
把 的坐标代入 ,得 , ,
抛物线的表达式为 .
(2)若点 是抛物线上点 与点 之间的动点(不包括点 、点 ,求
的面积的最大值,并求出此时点 的坐标.
解法一 设直线 的函数表达式为
,
, , 解得
直线 的函数表达式为 .
如图,过点 作 轴于点 ,交直线 于点 .
设 , ,则 .
,
.
当 时, 有最大值,最大值为 ,此时点 的纵坐标为
,
的面积的最大值为 ,此时点 的坐标为 , .
解法二 如图,将直线 平移,使其与抛物线只有
一个交点 ,连接 ,此时 的面积最大.
由解法一知直线 的函数表达式为 ,
可设直线 的表达式为 .
联立,得 ,
即 .
由 ,得 .
由求根公式,得 ,此时 .
.
, , ,
.
的面积的最大值为 ,此时点 的坐标为 .
