2023-2024学年华东师大版数学九年级下册 27.2.2 直线与圆的位置关系课件-(共23张PPT)
文档属性
| 名称 | 2023-2024学年华东师大版数学九年级下册 27.2.2 直线与圆的位置关系课件-(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
27.2 与圆有关的位置关系
课时2 直线与圆的位置关系
过基础 教材必备知识精练
知识点1 直线与圆的位置关系的判定
1.[2022六盘水中考]如图是“光盘行动”的宣传海报,图中
餐盘与筷子可看成直线和圆的位置关系是( )
B
A.相切 B.相交 C.相离 D.平行
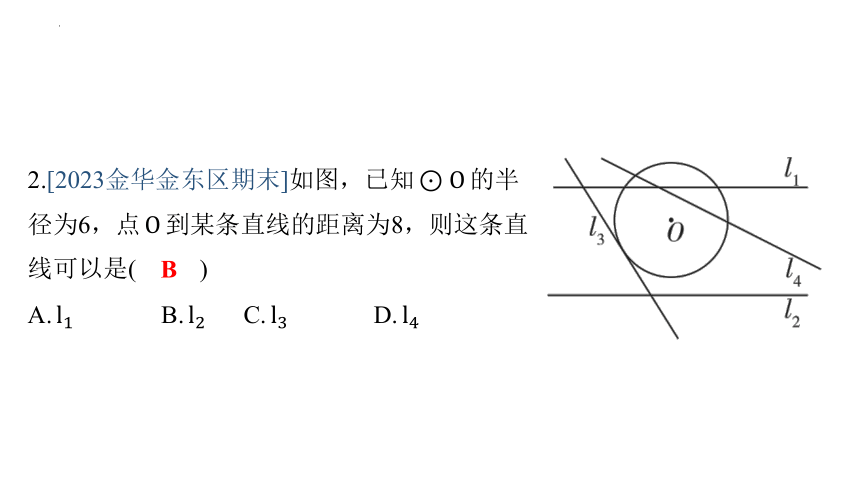
2.[2023金华金东区期末]如图,已知 的半
径为6,点 到某条直线的距离为8,则这条直
线可以是( )
B
A. B. C. D.
3.圆的直径为 ,如果圆心与直线的距离是 ,那么( )
C
A.当 时,直线与圆相交 B.当 时,直线与圆相离
C.当 时,直线与圆相切 D.当 时,直线与圆相切
【解析】 因为圆的直径为 ,所以圆的半径为 .当 时,直线与圆相切,当 时,直线与圆相交,当 时,直线与圆相离,故选项A,B,D错误,选项C正确.
4.新趋势·跨学科“金乌跃海映波红,栩栩升腾背向东.后羿挽弓怜万物,一
轮悬宇亮长空.”这首诗为我们描绘了太阳从海平面下逐渐升起,直至高挂
于天空的过程.将太阳抽象成圆,海平面抽象成直线,则在此过程中太阳
与海平面的位置关系是先______,再______,最后______.(填“相交”“相
离”或“相切”)
相交
相切
相离
【解析】 开始时,太阳与海平面“相交”;随着太阳的升起,太阳与海平面“相切”;当太阳“亮长空”时,太阳与海平面“相离”.
5.易错题[2023武汉新洲区第一初级中学练习]已知 的半径为 ,圆
心 到直线 上某点的距离为 ,则直线 与 的位置关系为______
______.
相切或相交
【解析】 的半径为 ,圆心 到直线 上某点的距离为 ,
圆心 到直线 的距离小于或等于 (易错点:切勿混淆圆心到直
线的距离与圆心到直线上一点的距离),即圆心 到直线 的距离小于或
等于圆的半径, 直线 和 相切或相交.
知识点2 直线与圆的位置关系的性质
6.教材P50练习 变式已知 的半径为3,直线 与 相离,则圆心
到直线 的距离 的取值范围是( )
B
A. B. C. D.
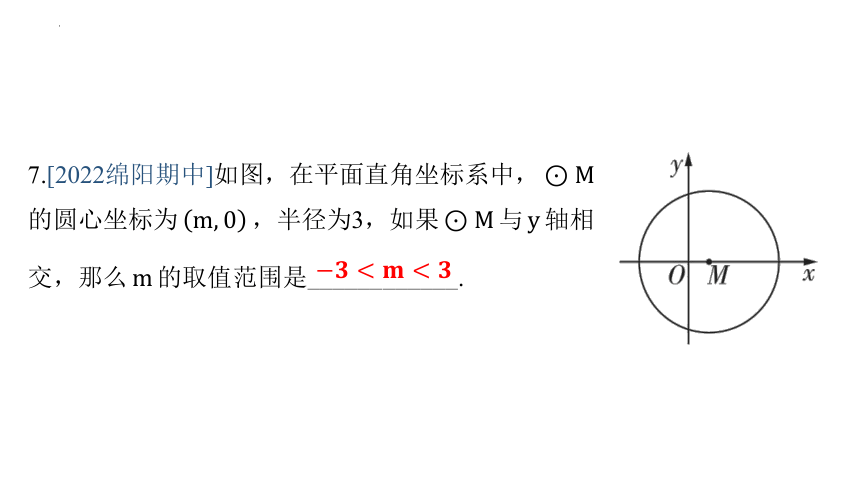
7.[2022绵阳期中]如图,在平面直角坐标系中,
的圆心坐标为 ,半径为3,如果 与 轴相
交,那么 的取值范围是_ ___________.
8.[2022韶关期末]如图,在半径为 的 中,直线 交
于 , 两点,且弦 ,要使直线 与 相切,求直线
需要向下平移的距离.
解:如图,过点 作 于点 ,连接 .
的半径为 ,弦 ,
, , . ,
要使直线 与 相切,则直线 需要向下平移 .
27.2 与圆有关的位置关系
课时2 直线与圆的位置关系
过能力 学科关键能力构建
1.[2022石家庄28中期末]如图, 的半径为1,
, ,则直线 与 的位置关系是
( )
A
A.相离 B.相切
C.相交 D.以上情况均有可能
【解析】 如图,过点 作 于点 ,在 中,
, ,所以 ( 角所对的
直角边等于斜边的一半),所以直线 与 的位置关系是相离.
2.已知 的半径 是一元二次方程 的一个根,圆心
到直线 的距离 ,则直线 与 的位置关系是( )
D
A.相交 B.相切 C.相离或相切 D.相交或相切
【解析】 &1&
3.[2022周口川汇区期末]在平面直角坐标系中,原点为 ,点 在函数
的图象上,以点 为圆心、 的长为半径的圆与直线
的位置关系是( )
B
A.相离 B.相切
C.相交 D.三种情况均有可能
【解析】 设 ,
抛物线的顶点坐标
为 , 点在直线 的上方, 点到直线 的距离
为 , 点到直线 的距离等于圆的半
径, 以点 为圆心、 的长为半径的圆与直线 的位置关系是
相切.
4.如图,直线 与 互相垂直,垂足为 , , ,垂足分别为点
, , , .以点 为圆心、 为半径作 ,根据下列条件,确
定 的取值范围:
(1)若 与两直线没有公共点,则 的取值范围为_ ____________;
(2)若 与两直线共有一个公共点,则 的取值范围为_ ________;
(3)若 与两直线共有两个公共点,则 的取值范围为_ ____________;
(4)若 与两直线共有三个公共点,则 的取值范围为______________
____;
或
(5)若 与两直线共有四个公共点,则 的取值范围为_ ______________.
且
5.如图, 为正比例函数 图象上的一个动点, 的半径为3,设点
的坐标为 .
(1)求 与直线 相切时点 的坐标.
解:过点 作直线 的垂线,垂足为 .
当点 在直线 的右侧时,
由 ,得 ,则 ;
当点 在直线 的左侧时,
由 ,得 ,则 .
当 与直线 相切时,点 的坐标为 或 .
(2)请直接写出 与直线 相交、相离时 的取值范围.
当 时, 与直线 相交;
当 或 时, 与直线 相离.
素养提升
6.运算能力[2022肇庆中学期末]如图,在矩形 中,
, ,点 在对角线 上, 的半径为2,如果
与矩形 的各边都没有公共点,那么线段 长的取
值范围是_ ____________.
【解析】 根据勾股定理,可得
.如图,当 与 相切时,
记点 为 ,设切点为 ,连接 ,则
.当 与 相切时,记点 为 ,
设切点为 ,连接 ,则 .分析可知,
当点 在点 , 之间时(不与点 , 重合), 与矩形
的各边都没有公共点. , ,
.同理可得 , .故线段 长的取值范围是
.
27.2 与圆有关的位置关系
课时2 直线与圆的位置关系
过基础 教材必备知识精练
知识点1 直线与圆的位置关系的判定
1.[2022六盘水中考]如图是“光盘行动”的宣传海报,图中
餐盘与筷子可看成直线和圆的位置关系是( )
B
A.相切 B.相交 C.相离 D.平行
2.[2023金华金东区期末]如图,已知 的半
径为6,点 到某条直线的距离为8,则这条直
线可以是( )
B
A. B. C. D.
3.圆的直径为 ,如果圆心与直线的距离是 ,那么( )
C
A.当 时,直线与圆相交 B.当 时,直线与圆相离
C.当 时,直线与圆相切 D.当 时,直线与圆相切
【解析】 因为圆的直径为 ,所以圆的半径为 .当 时,直线与圆相切,当 时,直线与圆相交,当 时,直线与圆相离,故选项A,B,D错误,选项C正确.
4.新趋势·跨学科“金乌跃海映波红,栩栩升腾背向东.后羿挽弓怜万物,一
轮悬宇亮长空.”这首诗为我们描绘了太阳从海平面下逐渐升起,直至高挂
于天空的过程.将太阳抽象成圆,海平面抽象成直线,则在此过程中太阳
与海平面的位置关系是先______,再______,最后______.(填“相交”“相
离”或“相切”)
相交
相切
相离
【解析】 开始时,太阳与海平面“相交”;随着太阳的升起,太阳与海平面“相切”;当太阳“亮长空”时,太阳与海平面“相离”.
5.易错题[2023武汉新洲区第一初级中学练习]已知 的半径为 ,圆
心 到直线 上某点的距离为 ,则直线 与 的位置关系为______
______.
相切或相交
【解析】 的半径为 ,圆心 到直线 上某点的距离为 ,
圆心 到直线 的距离小于或等于 (易错点:切勿混淆圆心到直
线的距离与圆心到直线上一点的距离),即圆心 到直线 的距离小于或
等于圆的半径, 直线 和 相切或相交.
知识点2 直线与圆的位置关系的性质
6.教材P50练习 变式已知 的半径为3,直线 与 相离,则圆心
到直线 的距离 的取值范围是( )
B
A. B. C. D.
7.[2022绵阳期中]如图,在平面直角坐标系中,
的圆心坐标为 ,半径为3,如果 与 轴相
交,那么 的取值范围是_ ___________.
8.[2022韶关期末]如图,在半径为 的 中,直线 交
于 , 两点,且弦 ,要使直线 与 相切,求直线
需要向下平移的距离.
解:如图,过点 作 于点 ,连接 .
的半径为 ,弦 ,
, , . ,
要使直线 与 相切,则直线 需要向下平移 .
27.2 与圆有关的位置关系
课时2 直线与圆的位置关系
过能力 学科关键能力构建
1.[2022石家庄28中期末]如图, 的半径为1,
, ,则直线 与 的位置关系是
( )
A
A.相离 B.相切
C.相交 D.以上情况均有可能
【解析】 如图,过点 作 于点 ,在 中,
, ,所以 ( 角所对的
直角边等于斜边的一半),所以直线 与 的位置关系是相离.
2.已知 的半径 是一元二次方程 的一个根,圆心
到直线 的距离 ,则直线 与 的位置关系是( )
D
A.相交 B.相切 C.相离或相切 D.相交或相切
【解析】 &1&
3.[2022周口川汇区期末]在平面直角坐标系中,原点为 ,点 在函数
的图象上,以点 为圆心、 的长为半径的圆与直线
的位置关系是( )
B
A.相离 B.相切
C.相交 D.三种情况均有可能
【解析】 设 ,
抛物线的顶点坐标
为 , 点在直线 的上方, 点到直线 的距离
为 , 点到直线 的距离等于圆的半
径, 以点 为圆心、 的长为半径的圆与直线 的位置关系是
相切.
4.如图,直线 与 互相垂直,垂足为 , , ,垂足分别为点
, , , .以点 为圆心、 为半径作 ,根据下列条件,确
定 的取值范围:
(1)若 与两直线没有公共点,则 的取值范围为_ ____________;
(2)若 与两直线共有一个公共点,则 的取值范围为_ ________;
(3)若 与两直线共有两个公共点,则 的取值范围为_ ____________;
(4)若 与两直线共有三个公共点,则 的取值范围为______________
____;
或
(5)若 与两直线共有四个公共点,则 的取值范围为_ ______________.
且
5.如图, 为正比例函数 图象上的一个动点, 的半径为3,设点
的坐标为 .
(1)求 与直线 相切时点 的坐标.
解:过点 作直线 的垂线,垂足为 .
当点 在直线 的右侧时,
由 ,得 ,则 ;
当点 在直线 的左侧时,
由 ,得 ,则 .
当 与直线 相切时,点 的坐标为 或 .
(2)请直接写出 与直线 相交、相离时 的取值范围.
当 时, 与直线 相交;
当 或 时, 与直线 相离.
素养提升
6.运算能力[2022肇庆中学期末]如图,在矩形 中,
, ,点 在对角线 上, 的半径为2,如果
与矩形 的各边都没有公共点,那么线段 长的取
值范围是_ ____________.
【解析】 根据勾股定理,可得
.如图,当 与 相切时,
记点 为 ,设切点为 ,连接 ,则
.当 与 相切时,记点 为 ,
设切点为 ,连接 ,则 .分析可知,
当点 在点 , 之间时(不与点 , 重合), 与矩形
的各边都没有公共点. , ,
.同理可得 , .故线段 长的取值范围是
.
