第26章 二次函数专项一: 二次函数的图象信息题课件(23张PPT)2023-2024学年华东师大版数学九年级下册
文档属性
| 名称 | 第26章 二次函数专项一: 二次函数的图象信息题课件(23张PPT)2023-2024学年华东师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第26章 二次函数
专项1 二次函数的图象信息题
过专项 阶段强化专项训练
解法归纳
1.根据抛物线开口方向判断 开口向上, ;开口向下, .
2.由 和对称轴的位置判断 规律是“左同右异”,即对称轴在 轴左
侧, , 同号;对称轴在 轴右侧, , 异号.
3.由抛物线与 轴的交点位置判断 交于正半轴, ;交于负半
轴, ;交于原点, .
4.特殊式子的判断:已知抛物线 ,看到 ,令 ;看到 ,令 ;看到 ,令 ;看到 ,令 ,然后看纵坐标.
5.根据 或 判断 的符号;根据 或 判断 的符号
类型1 函数图象共存问题
1.[2023河南中考]二次函数 的图象如图所
示,则一次函数 的图象一定不经过( )
D
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 由题图可得 , , ,
的图象经过第一、二、三象限,不经过第
四象限.
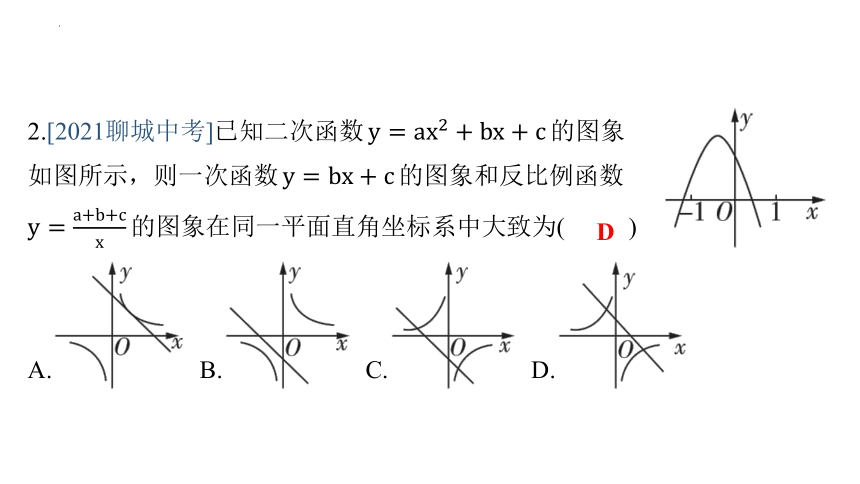
2.[2021聊城中考]已知二次函数 的图象
如图所示,则一次函数 的图象和反比例函数
的图象在同一平面直角坐标系中大致为( )
D
A.&1& B.&2& C.&3& D.&4&
【解析】 因为抛物线开口向下,所以 .因为 ,所以 .因为抛物线与 轴相交于正半轴,所以 ,所以直线 经过第一、二、四象限.由题图可知,当 时, ,所以 ,所以反比例函数 的图象必在第二、四象限,故选项A,B,C错误,选项D正确.
类型2函 数图象与 , , 之间的关系
3.[2023眉山中考]如图,二次函数 的图
象与 轴的一个交点的坐标为 ,对称轴为直线 ,
给出下列四个结论:① ;② ;
③ ;④当 时, .其中正确
结论的个数为( )
D
A.1 B.2 C.3 D.4
【解析】 抛物线 开口向上,与 轴交于负半
轴, , 该抛物线的对称轴为直线 ,
, , ,故①正确. 抛物线
与 轴的一个交点的坐标为 , 该抛物线
与 轴的另一个交点的坐标为 , 当 时,
,当 时, , ,故②④正
确.当 时, , , ,
,故③正确.
4.[2022广元中考]二次函数
的部分图象如图所示,图象过点 ,对称轴为
直线 .给出下列结论:① ;②
;③ ;④若点 、
点 、点 在该函数图象上,则
;⑤ ( 为常
数).其中正确的结论有( )
C
A.5个 B.4个 C.3个 D.2个
【解析】 抛物线的开口向下, 抛物线的对称轴为直线
, 抛物线与 轴交于正半轴, ,
,①正确. , 抛物线经过点 ,
, ,
, ,
,②不正确. ,③正确.
, , , ,④错误.
当 时, , ,
( 为常数),⑤正确.
第26章 二次函数
专项2 数学思想方法在二次函数中的应用
过专项 阶段强化专项训练
类型1 数形结合思想在二次函数中的应用
1.[2022山西中考]阅读与思考
下面是小宇同学的数学小论文,请仔细阅读并完成相应的任务.
用函数观点认识一元二次方程根的情况
我们知道,一元二次方程 的根就是相应的
二次函数 的图象(称为抛物线)与 轴交点的
横坐标.抛物线与 轴的交点有三种情况:有两个交点、有一个交点、无
交点.与此相对应,一元二次方程的根也有三种情况:有两个不相等的实
数根、有两个相等的实数根、无实数根.因此可用抛物线与 轴的交点个
数确定一元二次方程根的情况.
下面根据抛物线的顶点坐标 , 和一元二次方程根的判
别式 ,分 和 两种情况进行分析:
(1) 时,抛物线开口向上.
①当 时,有 , 顶点纵坐
标 , 顶点在 轴的下方,抛物线与 轴有两个交点(如图
1), 一元二次方程 有两个不相等的实数根.
__________________________________________________________________
图1
图2
续表
②当 时,有 , 顶点纵坐
标 , 顶点在 轴上,抛物线与 轴有一个交点(如图
2), 一元二次方程 有两个相等的实数根.
③当 时,
(2) 时,抛物线开口向下.
……
续表
任务
(1)上面小论文中的分析过程,主要运用的数学思想是_______________
______.(从下面选项中选出两个即可)
A, ,D或C,
A.数形结合 B.统计思想 C.分类讨论 D.转化思想
(2)请参照小论文中当 时①②的分析过程,写出③中当 ,
时,一元二次方程根的情况的分析过程,并画出相应的示意图.
当 时,有 ,
顶点纵坐标 , 顶点在 轴的上方,抛物线
与 轴无交点,如图, 一元二次方程
无实数根.
(3)实际上,除一元二次方程外,初中数学还有一些知识也可以用函数
观点来认识.例如:可用函数观点来认识一元一次方程的解.请你再举出一
例为__________________________________________________.
可用函数观点认识二元一次方程组的解(答案不唯一)
类型2 分类讨论思想在二次函数中的应用
2.[2023南充中考]抛物线 与 轴的一个交点为
,若 ,求实数 的取值范围.
解: 抛物线 与 轴有交点,
, ,解得 或 .
抛物线 的对称轴为直线 .
①当 时,抛物线的对称轴在直线 左侧,
此时抛物线 与 轴的一个交点为 ,
,如图1,
,解得 ;
图1
②当 时,抛物线的对称轴在直线 右侧,
此时抛物线 与 轴的一个交点为 ,
,如图2,
,解得 , .
综上, 或 .
图2
第26章 二次函数
专项1 二次函数的图象信息题
过专项 阶段强化专项训练
解法归纳
1.根据抛物线开口方向判断 开口向上, ;开口向下, .
2.由 和对称轴的位置判断 规律是“左同右异”,即对称轴在 轴左
侧, , 同号;对称轴在 轴右侧, , 异号.
3.由抛物线与 轴的交点位置判断 交于正半轴, ;交于负半
轴, ;交于原点, .
4.特殊式子的判断:已知抛物线 ,看到 ,令 ;看到 ,令 ;看到 ,令 ;看到 ,令 ,然后看纵坐标.
5.根据 或 判断 的符号;根据 或 判断 的符号
类型1 函数图象共存问题
1.[2023河南中考]二次函数 的图象如图所
示,则一次函数 的图象一定不经过( )
D
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 由题图可得 , , ,
的图象经过第一、二、三象限,不经过第
四象限.
2.[2021聊城中考]已知二次函数 的图象
如图所示,则一次函数 的图象和反比例函数
的图象在同一平面直角坐标系中大致为( )
D
A.&1& B.&2& C.&3& D.&4&
【解析】 因为抛物线开口向下,所以 .因为 ,所以 .因为抛物线与 轴相交于正半轴,所以 ,所以直线 经过第一、二、四象限.由题图可知,当 时, ,所以 ,所以反比例函数 的图象必在第二、四象限,故选项A,B,C错误,选项D正确.
类型2函 数图象与 , , 之间的关系
3.[2023眉山中考]如图,二次函数 的图
象与 轴的一个交点的坐标为 ,对称轴为直线 ,
给出下列四个结论:① ;② ;
③ ;④当 时, .其中正确
结论的个数为( )
D
A.1 B.2 C.3 D.4
【解析】 抛物线 开口向上,与 轴交于负半
轴, , 该抛物线的对称轴为直线 ,
, , ,故①正确. 抛物线
与 轴的一个交点的坐标为 , 该抛物线
与 轴的另一个交点的坐标为 , 当 时,
,当 时, , ,故②④正
确.当 时, , , ,
,故③正确.
4.[2022广元中考]二次函数
的部分图象如图所示,图象过点 ,对称轴为
直线 .给出下列结论:① ;②
;③ ;④若点 、
点 、点 在该函数图象上,则
;⑤ ( 为常
数).其中正确的结论有( )
C
A.5个 B.4个 C.3个 D.2个
【解析】 抛物线的开口向下, 抛物线的对称轴为直线
, 抛物线与 轴交于正半轴, ,
,①正确. , 抛物线经过点 ,
, ,
, ,
,②不正确. ,③正确.
, , , ,④错误.
当 时, , ,
( 为常数),⑤正确.
第26章 二次函数
专项2 数学思想方法在二次函数中的应用
过专项 阶段强化专项训练
类型1 数形结合思想在二次函数中的应用
1.[2022山西中考]阅读与思考
下面是小宇同学的数学小论文,请仔细阅读并完成相应的任务.
用函数观点认识一元二次方程根的情况
我们知道,一元二次方程 的根就是相应的
二次函数 的图象(称为抛物线)与 轴交点的
横坐标.抛物线与 轴的交点有三种情况:有两个交点、有一个交点、无
交点.与此相对应,一元二次方程的根也有三种情况:有两个不相等的实
数根、有两个相等的实数根、无实数根.因此可用抛物线与 轴的交点个
数确定一元二次方程根的情况.
下面根据抛物线的顶点坐标 , 和一元二次方程根的判
别式 ,分 和 两种情况进行分析:
(1) 时,抛物线开口向上.
①当 时,有 , 顶点纵坐
标 , 顶点在 轴的下方,抛物线与 轴有两个交点(如图
1), 一元二次方程 有两个不相等的实数根.
__________________________________________________________________
图1
图2
续表
②当 时,有 , 顶点纵坐
标 , 顶点在 轴上,抛物线与 轴有一个交点(如图
2), 一元二次方程 有两个相等的实数根.
③当 时,
(2) 时,抛物线开口向下.
……
续表
任务
(1)上面小论文中的分析过程,主要运用的数学思想是_______________
______.(从下面选项中选出两个即可)
A, ,D或C,
A.数形结合 B.统计思想 C.分类讨论 D.转化思想
(2)请参照小论文中当 时①②的分析过程,写出③中当 ,
时,一元二次方程根的情况的分析过程,并画出相应的示意图.
当 时,有 ,
顶点纵坐标 , 顶点在 轴的上方,抛物线
与 轴无交点,如图, 一元二次方程
无实数根.
(3)实际上,除一元二次方程外,初中数学还有一些知识也可以用函数
观点来认识.例如:可用函数观点来认识一元一次方程的解.请你再举出一
例为__________________________________________________.
可用函数观点认识二元一次方程组的解(答案不唯一)
类型2 分类讨论思想在二次函数中的应用
2.[2023南充中考]抛物线 与 轴的一个交点为
,若 ,求实数 的取值范围.
解: 抛物线 与 轴有交点,
, ,解得 或 .
抛物线 的对称轴为直线 .
①当 时,抛物线的对称轴在直线 左侧,
此时抛物线 与 轴的一个交点为 ,
,如图1,
,解得 ;
图1
②当 时,抛物线的对称轴在直线 右侧,
此时抛物线 与 轴的一个交点为 ,
,如图2,
,解得 , .
综上, 或 .
图2
