27.1.3圆周角 课件(48张PPT)2023-2024学年华东师大版数学九年级下册
文档属性
| 名称 | 27.1.3圆周角 课件(48张PPT)2023-2024学年华东师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 10:19:15 | ||
图片预览



文档简介
(共48张PPT)
27.1 圆的认识
课时4 圆周角
过基础 教材必备知识精练
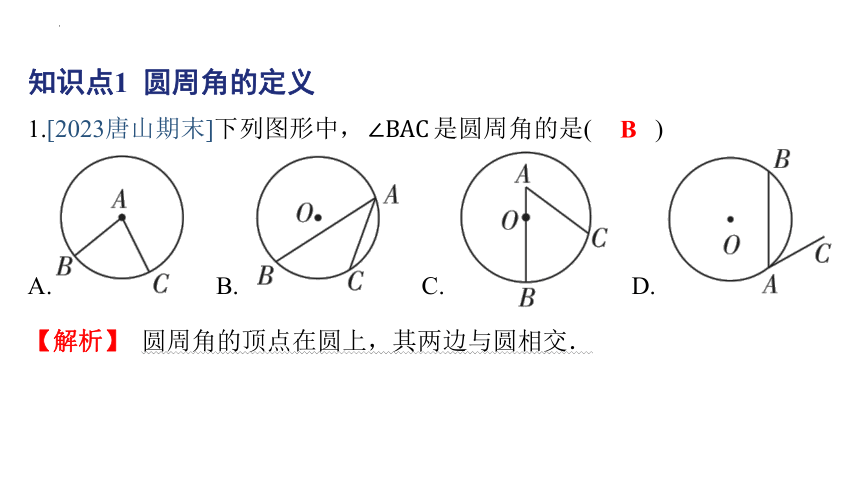
知识点1 圆周角的定义
1.[2023唐山期末]下列图形中, 是圆周角的是( )
B
A.&1& B.&2& C.&3& D.&4&
【解析】 圆周角的顶点在圆上,其两边与圆相交.
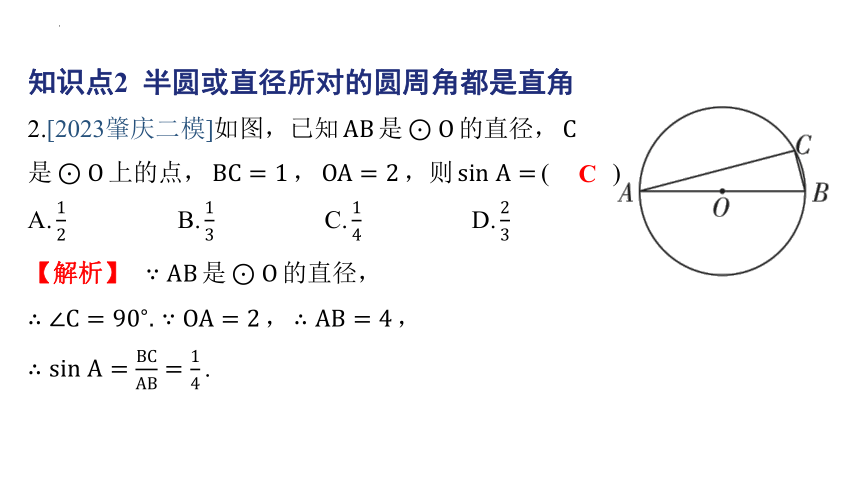
知识点2 半圆或直径所对的圆周角都是直角
2.[2023肇庆二模]如图,已知 是 的直径,
是 上的点, , ,则 ( )
C
A. B. C. D.
【解析】 是 的直径,
, ,
.
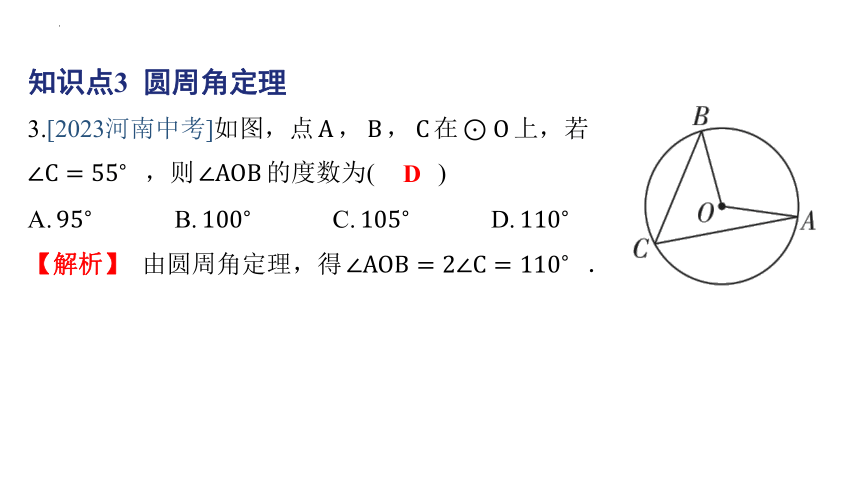
知识点3 圆周角定理
3.[2023河南中考]如图,点 , , 在 上,若
,则 的度数为( )
D
A. B. C. D.
【解析】 由圆周角定理,得 .
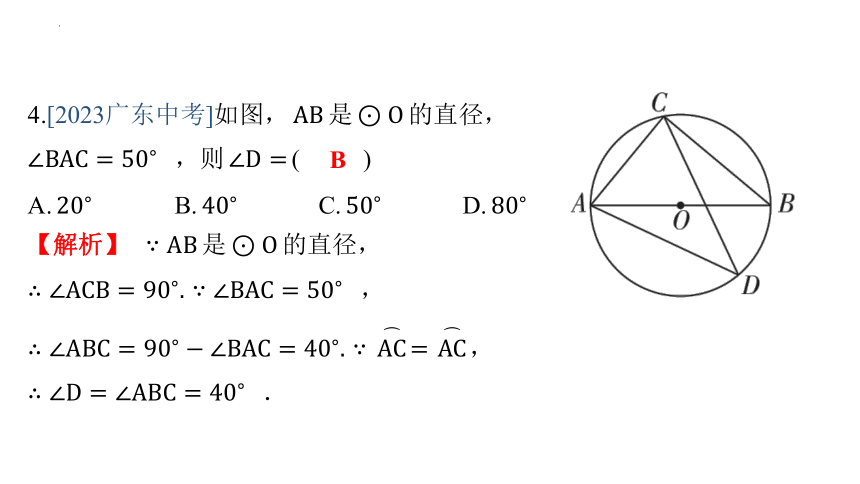
4.[2023广东中考]如图, 是 的直径,
,则 ( )
B
A. B. C. D.
【解析】 是 的直径,
,
,
.
5.[2023枣庄中考]如图,在 中,弦 , 相交于
点 .若 , ,则 的度数为
_ ____.
【解析】 , , .
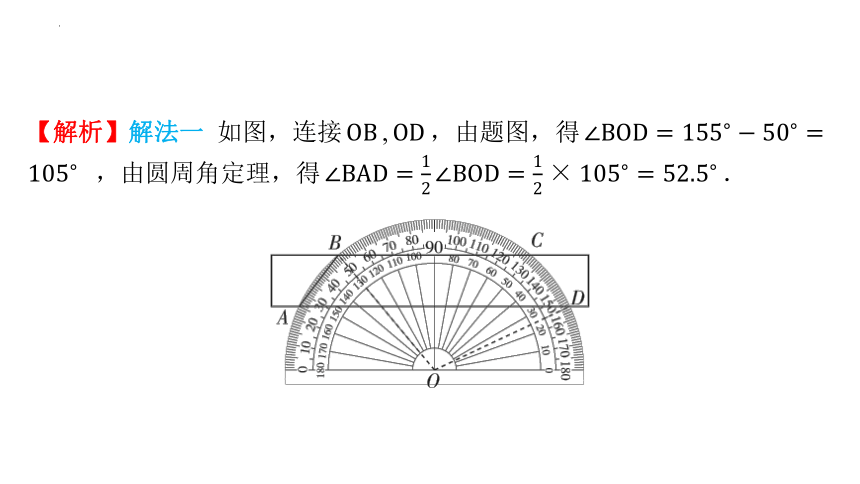
6.一题多解[2023烟台中考]如图,将一个
量角器与一把无刻度直尺水平摆放,直
尺的长边与量角器的外弧分别交于点
, , , ,连接 ,则 的
度数为_ ______.
【解析】解法一 如图,连接 , ,由题图,得
,由圆周角定理,得 .
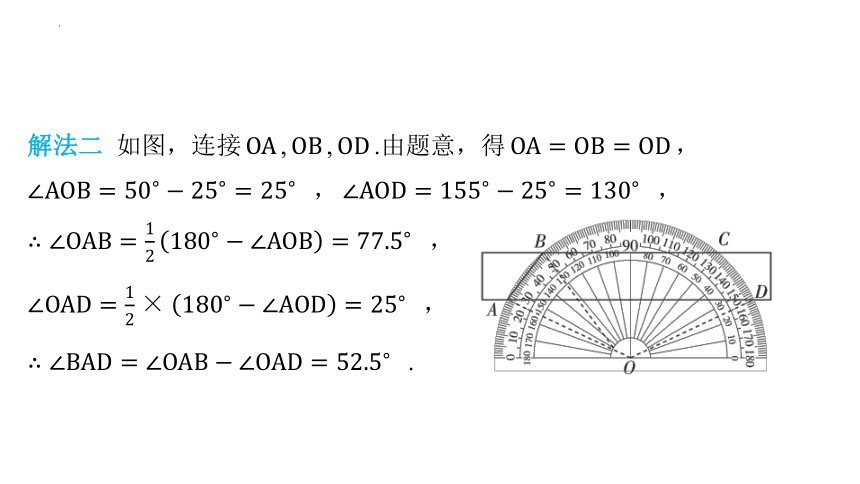
解法二 如图,连接 , , .由题意,得 ,
, ,
,
,
.
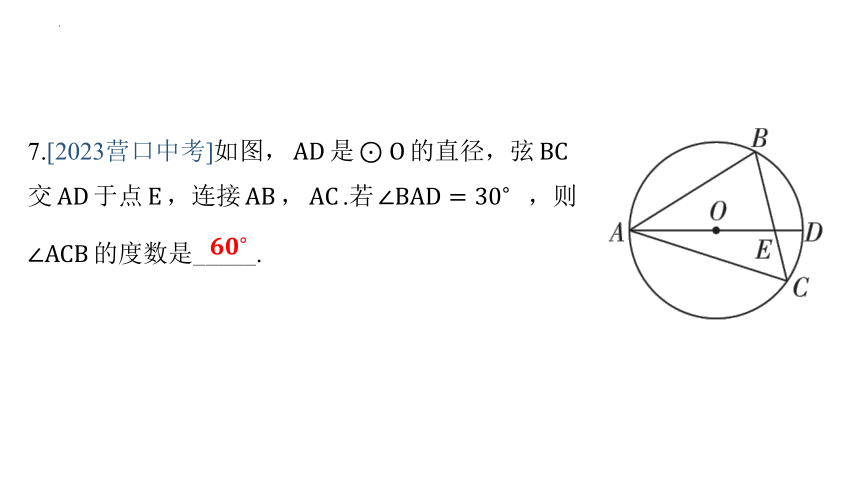
7.[2023营口中考]如图, 是 的直径,弦
交 于点 ,连接 , .若 ,则
的度数是_ ____.
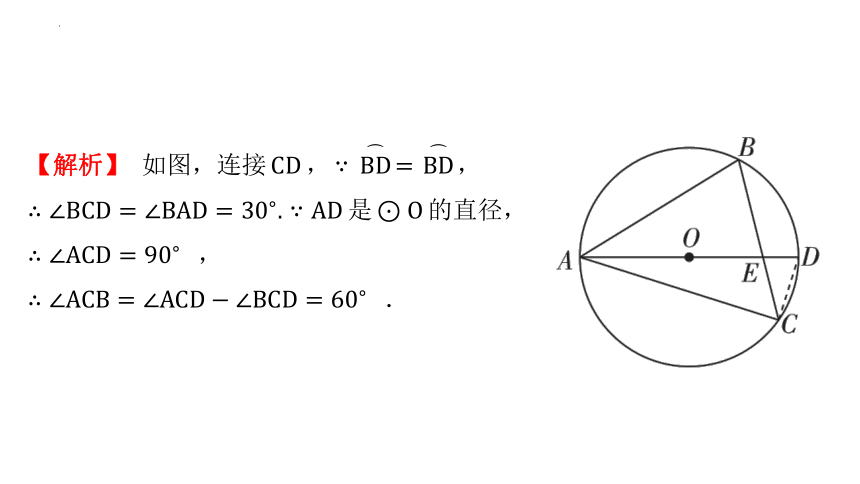
【解析】 如图,连接 , ,
是 的直径,
,
.
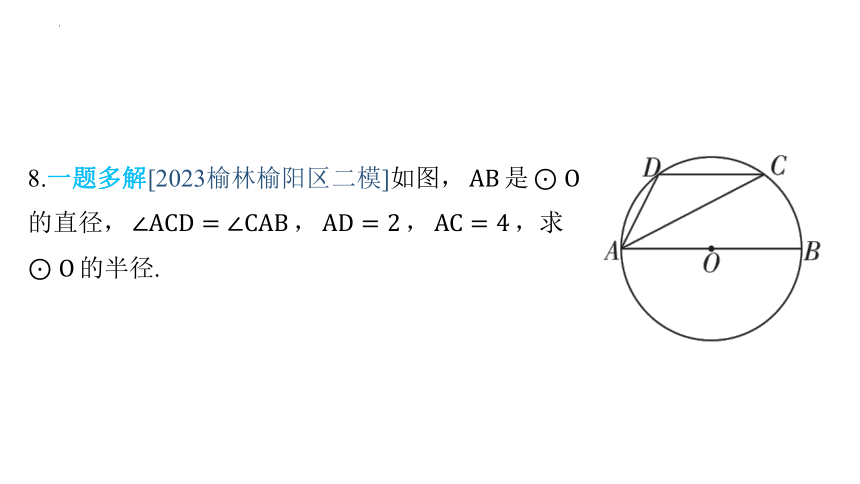
8.一题多解[2023榆林榆阳区二模]如图, 是
的直径, , , ,求
的半径.
解:解法一 连接 ,如图1,
, , .
为 的直径, ,
, .
图1
解法二 如图2,连接 并延长交 于点 ,连接 , , .
, ,
, .
是 的直径, .
在 中, , ,
, 的半径为 .
图2
知识点4 圆周角定理的推论
9.教材P44练习T3变式[2023台州期中]某圆形工件需要找出圆心,且只有
一块足够大的直角三角板(无刻度)可以使用,为此同学们需要先得到两
条不同的直径,下列寻找直径 的方法正确的是( )
B
A.&5& B.&6& C.&7& D.&8&
【解析】 的圆周角所对的弦是直径.
10.[2023绍兴中考]如图,四边形 内接于圆 ,
若 ,则 的度数是_ ____.
【解析】 四边形 内接于 , , .
11.[2023泰安中考]如图, 是 的直径, , 是
上的点.若 ,则 的度数是_ ____.
【解析】 , 是 的直径, , .
27.1 圆的认识
课时4 圆周角
过能力 学科关键能力构建
1.2023牡丹江中考T4变式如图,在圆内接四边形
中, ,连接 , , , ,
,则 的度数是( )
A
A. B. C. D.
【解析】 , , , , .
2.[2022福州期中]如图, 是 的直径,点 ,
, 在 上 .若 ,则 的度数为
( )
B
A. B. C. D.
【解析】 &9& .
3.[2023凉山州中考]如图,在 中, ,
, ,则 ( )
B
A.1 B.2 C. D.4
【解析】 如图,连接 , ,
,
, .在
中, , , .
4.新情境[2023郴州中考]如图,某博览会上有一圆形
展示区,在其圆形边缘的点 处安装了一台监视器,
它的监控角度是 ,为了监控整个展区,最少需
要在圆形边缘上安装这样的监视器___台.
4
【解析】 , 对应的圆心角为
, 最少需要在圆形边
缘上安装这样的监视器4台.
5.[2023重庆中考A卷]如图, 是矩形 的外接圆,
若 , ,则图中阴影部分的面积为_ ________.
(结果保留
【解析】 连接 ,易得 是 的直径. ,
, , 的半径为
, 的面积为 ,矩形的面积为
, 图中阴影部分的面积为 .
6.如图,四边形 内接于 , 交 的延
长线于点 .若 平分 , , ,则
_ _____.
【解析】 如图,连接 .
7.一题多解[2023包头中考]如图, 是 的直径, 是弦, 是
上的一点, 是 延长线上的一点,连接 , , .
(1)求证: .(请用两种证法解答)
证明:证法一 如图1,连接 ,
, .
是 的直径, .
, ,
.
图1
证法二 如图2,连接 ,
四边形 是 的内接四边形,
.
是 的直径, ,
, ,
.
图2
(2)若 , 的半径为3, ,求 的长.
图3
解:如图3,连接 ,
, ,
.
, ,
, .
的半径为3, .
在 中, ,
, , .
素养提升
8.运算能力[2023苏州中考]如图, 是半圆 的直径,
点 , 在半圆上, ,连接 , , ,过
点 作 ,交 的延长线于点 .设 的
面积为 , 的面积为 .
若 ,则 的值为( )
A
A. B. C. D.
【解析】 如图,过点 作 于点 ,
, ,
,
, . ,
, , .设 ,则
, ,
, .
一题多变
利用圆周角定理解决动点问题
1.母题如图,四边形 中的三个顶点在 上,点
是优弧 上的一个动点(不与点 , 重合).当圆心
在 内部, 时,求
的度数.
解:如图,连接 , , ,
, ,
,即
,
.
2.条件变为四边形 为平行四边形如图,平行四边形 中的三个
顶点在 上,点 是优弧 上的一个动点(不与点 , 重合).当
圆心 在 内部时,求 的度数.
解: 四边形 为平行四边形, .
, .
,即 , .
3.条件与结论互换如图,平行四边形 中的三个顶点
在 上,点 是优弧 上的一个动点(不与点 ,
重合).当圆心 在 内部时,试确定 与
的数量关系并说明理由.
解: .理由如下:
如图,连接 ,易知 (注:由第2题的结论可
知).
, ,
, ,
.
4.变为圆心 在 外部如图,平行四边形 中
的三个顶点在 上,点 是优弧 上的一个动点
(不与点 , 重合).当圆心 在 外部时,请
画出图形,确定 与 的数量关系并说明理
由.
解: .理由如下:
易知 ,如图1,连接 ,
, .
, .
,
,即 .
图1
如图2,同理可得 ,即 .
综上, 与 的数量关系为 .
图2
27.1 圆的认识
课时4 圆周角
过基础 教材必备知识精练
知识点1 圆周角的定义
1.[2023唐山期末]下列图形中, 是圆周角的是( )
B
A.&1& B.&2& C.&3& D.&4&
【解析】 圆周角的顶点在圆上,其两边与圆相交.
知识点2 半圆或直径所对的圆周角都是直角
2.[2023肇庆二模]如图,已知 是 的直径,
是 上的点, , ,则 ( )
C
A. B. C. D.
【解析】 是 的直径,
, ,
.
知识点3 圆周角定理
3.[2023河南中考]如图,点 , , 在 上,若
,则 的度数为( )
D
A. B. C. D.
【解析】 由圆周角定理,得 .
4.[2023广东中考]如图, 是 的直径,
,则 ( )
B
A. B. C. D.
【解析】 是 的直径,
,
,
.
5.[2023枣庄中考]如图,在 中,弦 , 相交于
点 .若 , ,则 的度数为
_ ____.
【解析】 , , .
6.一题多解[2023烟台中考]如图,将一个
量角器与一把无刻度直尺水平摆放,直
尺的长边与量角器的外弧分别交于点
, , , ,连接 ,则 的
度数为_ ______.
【解析】解法一 如图,连接 , ,由题图,得
,由圆周角定理,得 .
解法二 如图,连接 , , .由题意,得 ,
, ,
,
,
.
7.[2023营口中考]如图, 是 的直径,弦
交 于点 ,连接 , .若 ,则
的度数是_ ____.
【解析】 如图,连接 , ,
是 的直径,
,
.
8.一题多解[2023榆林榆阳区二模]如图, 是
的直径, , , ,求
的半径.
解:解法一 连接 ,如图1,
, , .
为 的直径, ,
, .
图1
解法二 如图2,连接 并延长交 于点 ,连接 , , .
, ,
, .
是 的直径, .
在 中, , ,
, 的半径为 .
图2
知识点4 圆周角定理的推论
9.教材P44练习T3变式[2023台州期中]某圆形工件需要找出圆心,且只有
一块足够大的直角三角板(无刻度)可以使用,为此同学们需要先得到两
条不同的直径,下列寻找直径 的方法正确的是( )
B
A.&5& B.&6& C.&7& D.&8&
【解析】 的圆周角所对的弦是直径.
10.[2023绍兴中考]如图,四边形 内接于圆 ,
若 ,则 的度数是_ ____.
【解析】 四边形 内接于 , , .
11.[2023泰安中考]如图, 是 的直径, , 是
上的点.若 ,则 的度数是_ ____.
【解析】 , 是 的直径, , .
27.1 圆的认识
课时4 圆周角
过能力 学科关键能力构建
1.2023牡丹江中考T4变式如图,在圆内接四边形
中, ,连接 , , , ,
,则 的度数是( )
A
A. B. C. D.
【解析】 , , , , .
2.[2022福州期中]如图, 是 的直径,点 ,
, 在 上 .若 ,则 的度数为
( )
B
A. B. C. D.
【解析】 &9& .
3.[2023凉山州中考]如图,在 中, ,
, ,则 ( )
B
A.1 B.2 C. D.4
【解析】 如图,连接 , ,
,
, .在
中, , , .
4.新情境[2023郴州中考]如图,某博览会上有一圆形
展示区,在其圆形边缘的点 处安装了一台监视器,
它的监控角度是 ,为了监控整个展区,最少需
要在圆形边缘上安装这样的监视器___台.
4
【解析】 , 对应的圆心角为
, 最少需要在圆形边
缘上安装这样的监视器4台.
5.[2023重庆中考A卷]如图, 是矩形 的外接圆,
若 , ,则图中阴影部分的面积为_ ________.
(结果保留
【解析】 连接 ,易得 是 的直径. ,
, , 的半径为
, 的面积为 ,矩形的面积为
, 图中阴影部分的面积为 .
6.如图,四边形 内接于 , 交 的延
长线于点 .若 平分 , , ,则
_ _____.
【解析】 如图,连接 .
7.一题多解[2023包头中考]如图, 是 的直径, 是弦, 是
上的一点, 是 延长线上的一点,连接 , , .
(1)求证: .(请用两种证法解答)
证明:证法一 如图1,连接 ,
, .
是 的直径, .
, ,
.
图1
证法二 如图2,连接 ,
四边形 是 的内接四边形,
.
是 的直径, ,
, ,
.
图2
(2)若 , 的半径为3, ,求 的长.
图3
解:如图3,连接 ,
, ,
.
, ,
, .
的半径为3, .
在 中, ,
, , .
素养提升
8.运算能力[2023苏州中考]如图, 是半圆 的直径,
点 , 在半圆上, ,连接 , , ,过
点 作 ,交 的延长线于点 .设 的
面积为 , 的面积为 .
若 ,则 的值为( )
A
A. B. C. D.
【解析】 如图,过点 作 于点 ,
, ,
,
, . ,
, , .设 ,则
, ,
, .
一题多变
利用圆周角定理解决动点问题
1.母题如图,四边形 中的三个顶点在 上,点
是优弧 上的一个动点(不与点 , 重合).当圆心
在 内部, 时,求
的度数.
解:如图,连接 , , ,
, ,
,即
,
.
2.条件变为四边形 为平行四边形如图,平行四边形 中的三个
顶点在 上,点 是优弧 上的一个动点(不与点 , 重合).当
圆心 在 内部时,求 的度数.
解: 四边形 为平行四边形, .
, .
,即 , .
3.条件与结论互换如图,平行四边形 中的三个顶点
在 上,点 是优弧 上的一个动点(不与点 ,
重合).当圆心 在 内部时,试确定 与
的数量关系并说明理由.
解: .理由如下:
如图,连接 ,易知 (注:由第2题的结论可
知).
, ,
, ,
.
4.变为圆心 在 外部如图,平行四边形 中
的三个顶点在 上,点 是优弧 上的一个动点
(不与点 , 重合).当圆心 在 外部时,请
画出图形,确定 与 的数量关系并说明理
由.
解: .理由如下:
易知 ,如图1,连接 ,
, .
, .
,
,即 .
图1
如图2,同理可得 ,即 .
综上, 与 的数量关系为 .
图2
