4.1.2 认识三角形(第2课时) 课件(共25张PPT)
文档属性
| 名称 | 4.1.2 认识三角形(第2课时) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
新课标 北师大版
七年级下册
4.1.2认识三角形(2)
第四章
三角形
学习目标
1 掌握三角形按边分类的方法,能够判定三角形是否为特殊三角形;
2 掌握三角形的三边关系,能运用三角形三边关系解决有关的问题.
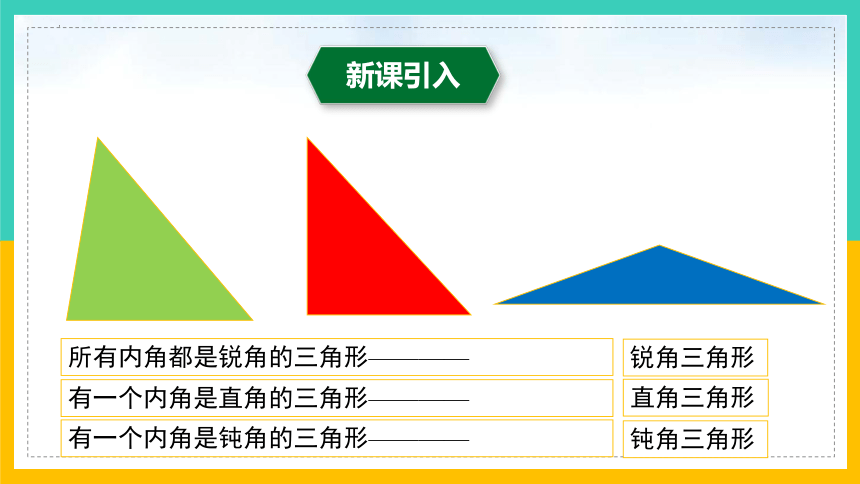
新课引入
所有内角都是锐角的三角形————
有一个内角是直角的三角形————
锐角三角形
直角三角形
钝角三角形
有一个内角是钝角的三角形————
新课引入
在一个由三条边构成的三角形小城里,老大仗着自己最长,常欺负老二和老三.一天,老二灵机一动,想出了对付老大的方法,他对老三说:“只要我们两合作,加起来一定比老大长,这样他就不敢再欺负我们了.”老大不信,无论怎么用力伸展变长,就是没有老二老三加起来长,老大终于意识到自己的不足了,从此再也不敢欺负老二和老三了.
同学们,你们知道其中的道理吗?
核心知识点一
探究学习
三角形按边分类
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
有两边相等的三角形叫做等腰三角形,
如图.三边都相等的三角形是等边三角形,也叫正三角形.
腰
腰
底边
顶角
底角
底角
等边三角形
三角形按
边分类
不等边三角形
等腰三角形
腰和底不等的等腰三角形
练一练:
1.等腰三角形一腰为3cm,底为4cm,则它的周长是__________;
2.等腰三角形的一边长为3cm,另一边长为4cm,则
它的周长是______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则
它的周长是__________.
10cm
10cm或11cm
19cm
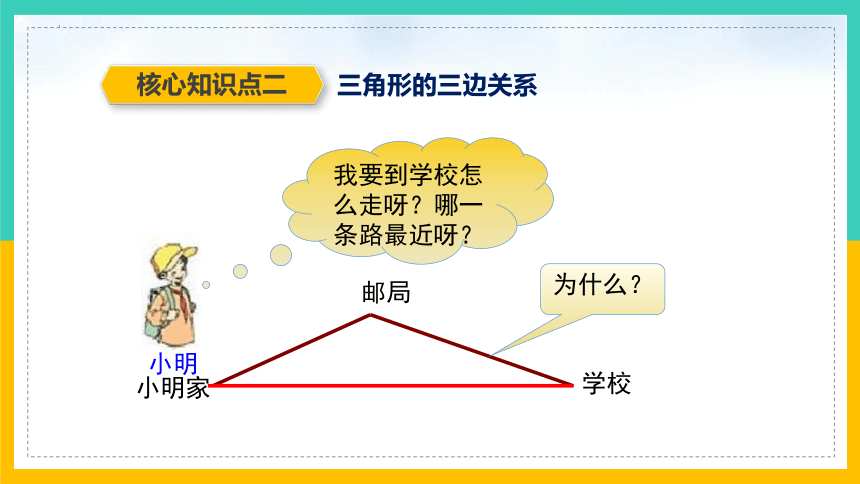
核心知识点二
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
B(学校)
C(邮局)
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
解:路线2较短;两点之间线段最短.
由此可以得到:
A(小明家)
请问:路线1、路线2哪条路程较短,你能说出根据吗?
分别量出(图4-14)三个三角形的三边长度,并填入空格内.
(1)a=________,
b=________,
c=________,
(2)a=________,
b=________,
c=________,
(3)a=________,
b=________,
c=________,
计算每个三角形的任意两边之差,并与第三边比较,
你能得到什么结论 再画一些三角形试一试.
议一议:
1.在同一个三角形中,任意两边之和与第三边有什么大小关系
2.在同一个三角形中,任意两边之差与第三边有什么大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三条线段能够组成三角形的判定条件
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
三角形的三边关系
例:有两根长度分别为 5 cm和 8 cm的木棒,用长度为 2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5 =7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
提示:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
通过多个条件确定三角形第三边的方法:
已知两边
第三边小于已知两边的和而大于已知两边的差
第三边的范围
附加条件
确定第三边
归纳总结
随堂练习
(2)等边三角形是特殊的等腰三角形;( )
(1)一个钝角三角形一定不是等腰三角形;( )
(3)等腰三角形的腰和底一定不相等;( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形;( )
×
√
2.长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
B
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7
C.5,6,12 D.6,8,10
C
4.下列长度的三根小木棒能构成三角形的是( )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4cm
D
7.如果等腰三角形的一边长是4cm,另一边长是9cm, 则这个等腰三角形的周长为________.
6.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
5.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长可以构成____个三角形.
3
22cm
18cm或21cm
8.三角形两边长分别为3和5,第三边的长可以是8吗?可以是2吗?说说你的理由.
解:不可以是8,也不可以是2.
理由:三角形任意两边之和大于第三边,任意两边之差小于第三边.
9.在△ABC中,a=4,b=2,若第三边c的长是偶数,求c的长.
解:在△ABC中,a=4,b=2,
所以a-b又因为c为偶数,
所以c=4.
课堂小结
谢谢聆听
新课标 北师大版
七年级下册
4.1.2认识三角形(2)
第四章
三角形
学习目标
1 掌握三角形按边分类的方法,能够判定三角形是否为特殊三角形;
2 掌握三角形的三边关系,能运用三角形三边关系解决有关的问题.
新课引入
所有内角都是锐角的三角形————
有一个内角是直角的三角形————
锐角三角形
直角三角形
钝角三角形
有一个内角是钝角的三角形————
新课引入
在一个由三条边构成的三角形小城里,老大仗着自己最长,常欺负老二和老三.一天,老二灵机一动,想出了对付老大的方法,他对老三说:“只要我们两合作,加起来一定比老大长,这样他就不敢再欺负我们了.”老大不信,无论怎么用力伸展变长,就是没有老二老三加起来长,老大终于意识到自己的不足了,从此再也不敢欺负老二和老三了.
同学们,你们知道其中的道理吗?
核心知识点一
探究学习
三角形按边分类
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
有两边相等的三角形叫做等腰三角形,
如图.三边都相等的三角形是等边三角形,也叫正三角形.
腰
腰
底边
顶角
底角
底角
等边三角形
三角形按
边分类
不等边三角形
等腰三角形
腰和底不等的等腰三角形
练一练:
1.等腰三角形一腰为3cm,底为4cm,则它的周长是__________;
2.等腰三角形的一边长为3cm,另一边长为4cm,则
它的周长是______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则
它的周长是__________.
10cm
10cm或11cm
19cm
核心知识点二
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
B(学校)
C(邮局)
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
解:路线2较短;两点之间线段最短.
由此可以得到:
A(小明家)
请问:路线1、路线2哪条路程较短,你能说出根据吗?
分别量出(图4-14)三个三角形的三边长度,并填入空格内.
(1)a=________,
b=________,
c=________,
(2)a=________,
b=________,
c=________,
(3)a=________,
b=________,
c=________,
计算每个三角形的任意两边之差,并与第三边比较,
你能得到什么结论 再画一些三角形试一试.
议一议:
1.在同一个三角形中,任意两边之和与第三边有什么大小关系
2.在同一个三角形中,任意两边之差与第三边有什么大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三条线段能够组成三角形的判定条件
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
三角形的三边关系
例:有两根长度分别为 5 cm和 8 cm的木棒,用长度为 2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5 =7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
提示:只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
通过多个条件确定三角形第三边的方法:
已知两边
第三边小于已知两边的和而大于已知两边的差
第三边的范围
附加条件
确定第三边
归纳总结
随堂练习
(2)等边三角形是特殊的等腰三角形;( )
(1)一个钝角三角形一定不是等腰三角形;( )
(3)等腰三角形的腰和底一定不相等;( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形;( )
×
√
2.长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A.4 B.5 C.6 D.7
B
3.下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7
C.5,6,12 D.6,8,10
C
4.下列长度的三根小木棒能构成三角形的是( )
A.2 cm,3 cm,5 cm
B.7 cm,4 cm,2 cm
C.3 cm,4 cm,8 cm
D.3 cm,3 cm,4cm
D
7.如果等腰三角形的一边长是4cm,另一边长是9cm, 则这个等腰三角形的周长为________.
6.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
5.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长可以构成____个三角形.
3
22cm
18cm或21cm
8.三角形两边长分别为3和5,第三边的长可以是8吗?可以是2吗?说说你的理由.
解:不可以是8,也不可以是2.
理由:三角形任意两边之和大于第三边,任意两边之差小于第三边.
9.在△ABC中,a=4,b=2,若第三边c的长是偶数,求c的长.
解:在△ABC中,a=4,b=2,
所以a-b
所以c=4.
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
