19.1.2 函数的表示方法(第2课时) 课件(共34张PPT)
文档属性
| 名称 | 19.1.2 函数的表示方法(第2课时) 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 17:50:39 | ||
图片预览







文档简介
(共34张PPT)
【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版)
19.1.2 函数的表示方法(第2课时)
第19章 一次函数
02
03
05
06
04
目
录
分层练习
新知探究
情景导入
课堂小结
课堂反馈
01
学习目标
1.了解函数的三种表示方法及其优点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;(重点)
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.(难点)
学习目标
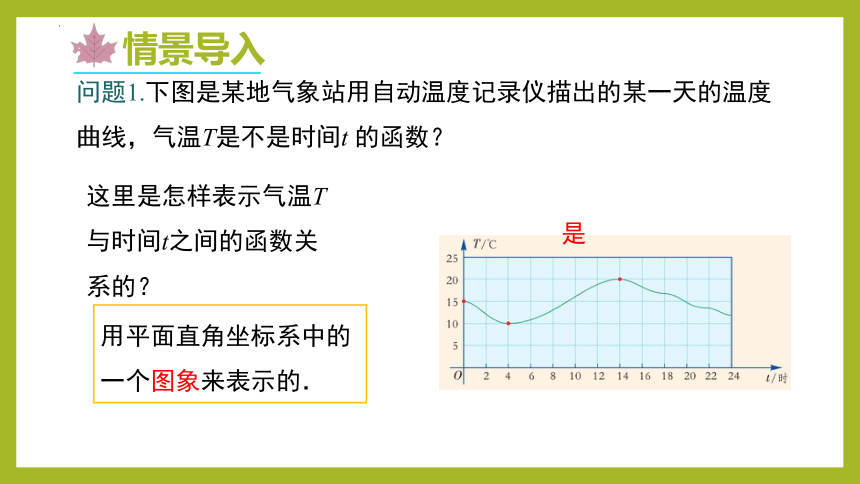
用平面直角坐标系中的一个图象来表示的.
问题1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
情景导入
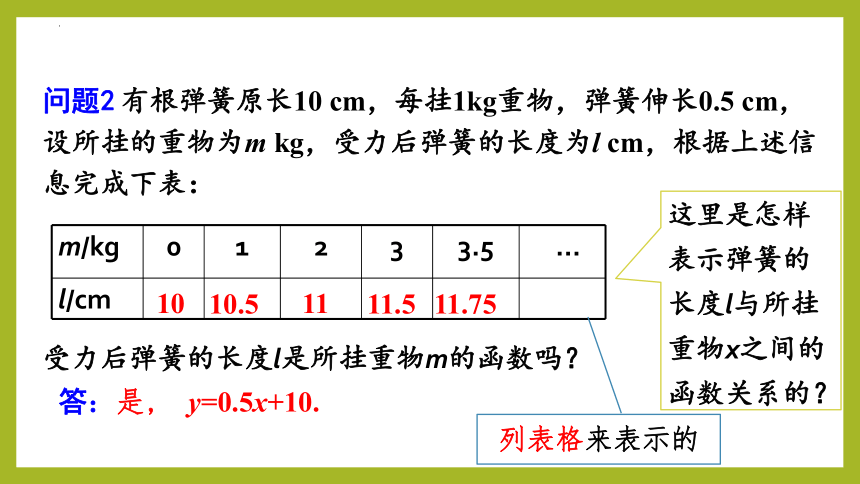
问题2 有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表:
受力后弹簧的长度l是所挂重物m的函数吗?
m/kg 0 1 2 3 3.5 …
l/cm
答:是, y=0.5x+10.
11.75
11.5
11
10.5
10
这里是怎样表示弹簧的长度l与所挂重物x之间的函数关系的?
列表格来表示的
问题3 有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了x(x>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?
答:是, y=8+2(x-3)
=2x+2
这里是怎样表示所付费用y与所走路程x的函数关系的?
用函数解析式来表示.
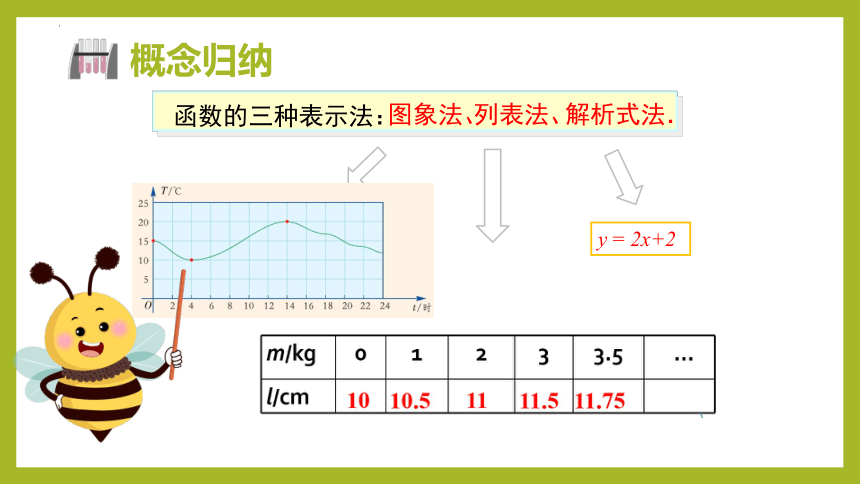
函数的三种表示法:
y = 2x+2
图象法、
列表法、
解析式法.
概念归纳
归纳总结
函数的三种表示方法:
(1)列表法:用_______列出自变量与函数的对应值,表示函数两个变量之间的关系,这种表示函数的方法叫做列表法.
(2)图象法:用_______表示两个变量之间的函数关系,这种表示函数的方法叫做图象法.
(3)解析式法:用__________表示函数的方法叫做解析式法.
表格
图象
数学式
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
这三种表示函数的方法各有什么优点?
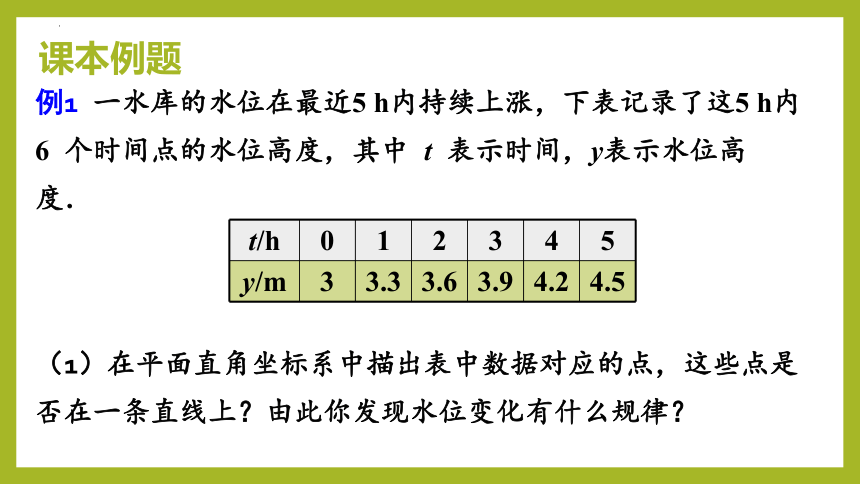
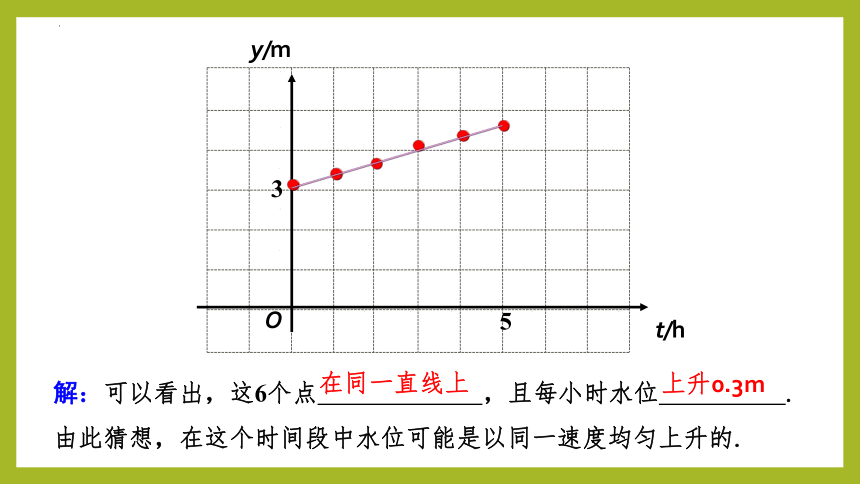
例1 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
课本例题
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
3
O
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
3
O
5
其函数的图象如下:
5
A
B
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n 3 4 5 6 …
m …
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
课本练习
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).
a … 1 2 3 4 …
l … 3 6 9 12 …
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
课本练习
3.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离(s)是时间(t)的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
s = 200-25t
船速度为(200-150)÷2=25m/min,
s=200-25t
课本练习
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
…
12
10
8
6
4
2
y(元)
…
6
5
4
3
2
1
x(支)
y=15-x
0<x<15
分层练习-基础
5.09
A
D
分层练习-基础
C
C
分层练习-巩固
A
分层练习-巩固
y=0.5x+12
分层练习-巩固
分层练习-巩固
分层练习-巩固
x 3 4 5 6 … 10 11
y 18 16
分层练习-拓展
分层练习-拓展
C
课堂反馈
课堂反馈
课堂反馈
课堂反馈
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结
【大单元教学】2023-2024学年八年级数学下册同步备课系列(人教版)
19.1.2 函数的表示方法(第2课时)
第19章 一次函数
02
03
05
06
04
目
录
分层练习
新知探究
情景导入
课堂小结
课堂反馈
01
学习目标
1.了解函数的三种表示方法及其优点;
2.能用适当的方式表示简单实际问题中的变量之间
的函数关系;(重点)
3.能对函数关系进行分析,对变量的变化情况进行
初步讨论.(难点)
学习目标
用平面直角坐标系中的一个图象来表示的.
问题1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
情景导入
问题2 有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表:
受力后弹簧的长度l是所挂重物m的函数吗?
m/kg 0 1 2 3 3.5 …
l/cm
答:是, y=0.5x+10.
11.75
11.5
11
10.5
10
这里是怎样表示弹簧的长度l与所挂重物x之间的函数关系的?
列表格来表示的
问题3 有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了x(x>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?
答:是, y=8+2(x-3)
=2x+2
这里是怎样表示所付费用y与所走路程x的函数关系的?
用函数解析式来表示.
函数的三种表示法:
y = 2x+2
图象法、
列表法、
解析式法.
概念归纳
归纳总结
函数的三种表示方法:
(1)列表法:用_______列出自变量与函数的对应值,表示函数两个变量之间的关系,这种表示函数的方法叫做列表法.
(2)图象法:用_______表示两个变量之间的函数关系,这种表示函数的方法叫做图象法.
(3)解析式法:用__________表示函数的方法叫做解析式法.
表格
图象
数学式
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
这三种表示函数的方法各有什么优点?
例1 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
课本例题
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
3
O
5
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
3
O
5
其函数的图象如下:
5
A
B
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:因为n表示的是多边形的边数,所以n是大于等于3的自然数,列表如下:
n 3 4 5 6 …
m …
所以m=(n-2)·180°(n≥3,且n为自然数).
180
360
540
720
提示:n边形的内角和公式是:(n-2) ×180°.
课本练习
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).
a … 1 2 3 4 …
l … 3 6 9 12 …
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
课本练习
3.一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离(s)是时间(t)的函数吗?
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
t/min 0 2 4 6 ……
s/m 200 150 100 50 ……
是
s = 200-25t
船速度为(200-150)÷2=25m/min,
s=200-25t
课本练习
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
…
12
10
8
6
4
2
y(元)
…
6
5
4
3
2
1
x(支)
y=15-x
0<x<15
分层练习-基础
5.09
A
D
分层练习-基础
C
C
分层练习-巩固
A
分层练习-巩固
y=0.5x+12
分层练习-巩固
分层练习-巩固
分层练习-巩固
x 3 4 5 6 … 10 11
y 18 16
分层练习-拓展
分层练习-拓展
C
课堂反馈
课堂反馈
课堂反馈
课堂反馈
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结
