24.5 三角形的内切圆
图片预览




文档简介
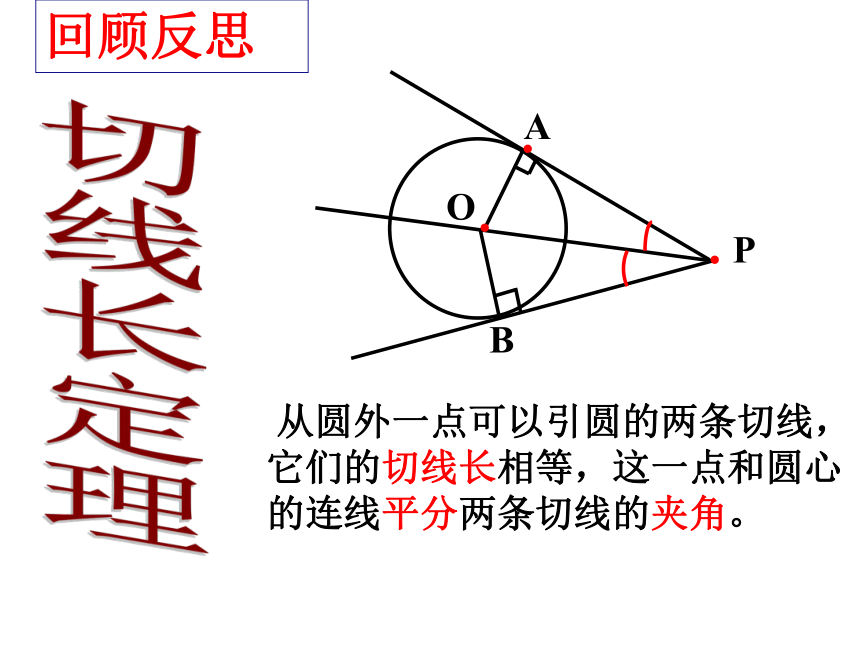
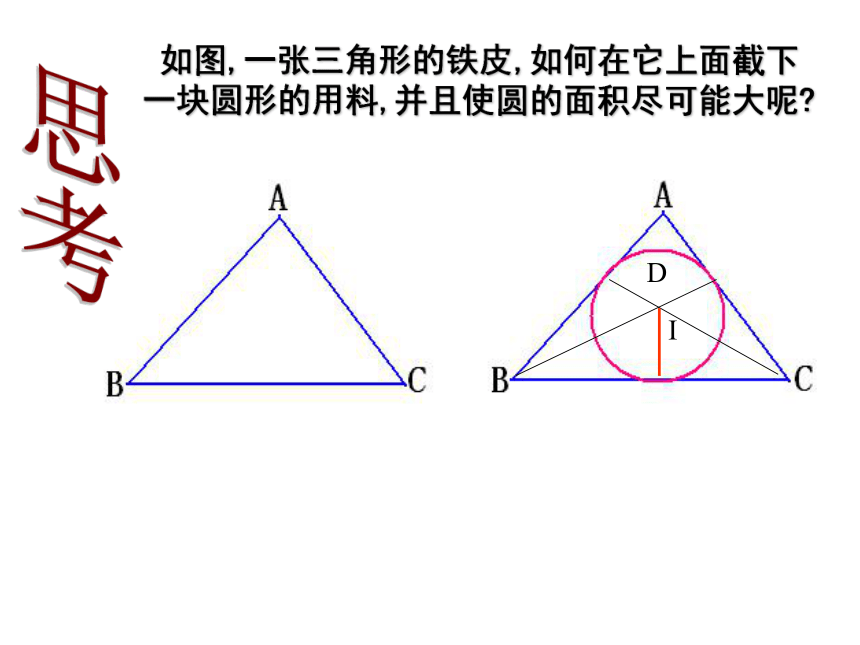
课件31张PPT。第24章 圆义门中心校 数学组九年级 上册24.5 三角形的内切圆回顾反思 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。切线长定理 如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?ID思考三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆三角形的内心:三角形的内切圆的圆心叫做三角形的内心三角形的内心是三角形三
条角平分线的交点,它到
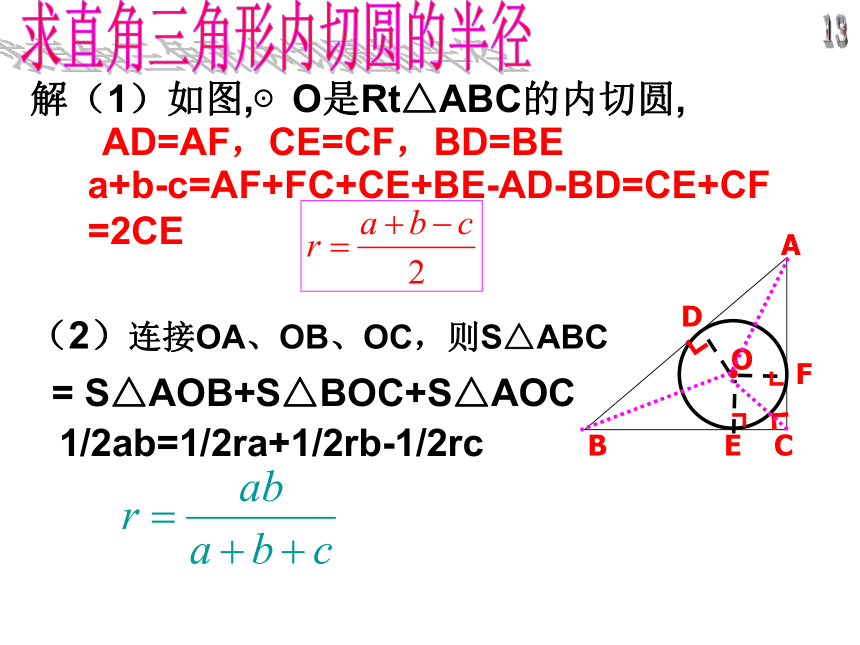
三角形三边的距离相等。概念介绍已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.求⊙O的半径r. Rt△的三边长与其内切圆半径间的关系探 究(1)求直角三角形内切圆的半径P43习题25、6 第 5题解(1)如图,⊙O是Rt△ABC的内切圆,13
求直角三角形内切圆的半径AD=AF,CE=CF,BD=BEa+b-c=AF+FC+CE+BE-AD-BD=CE+CF
=2CE = S△AOB+S△BOC+S△AOC1/2ab=1/2ra+1/2rb-1/2rc(2)连接OA、OB、OC,则S△ABC解(1)如图,⊙O是Rt△ABC的内切圆,13
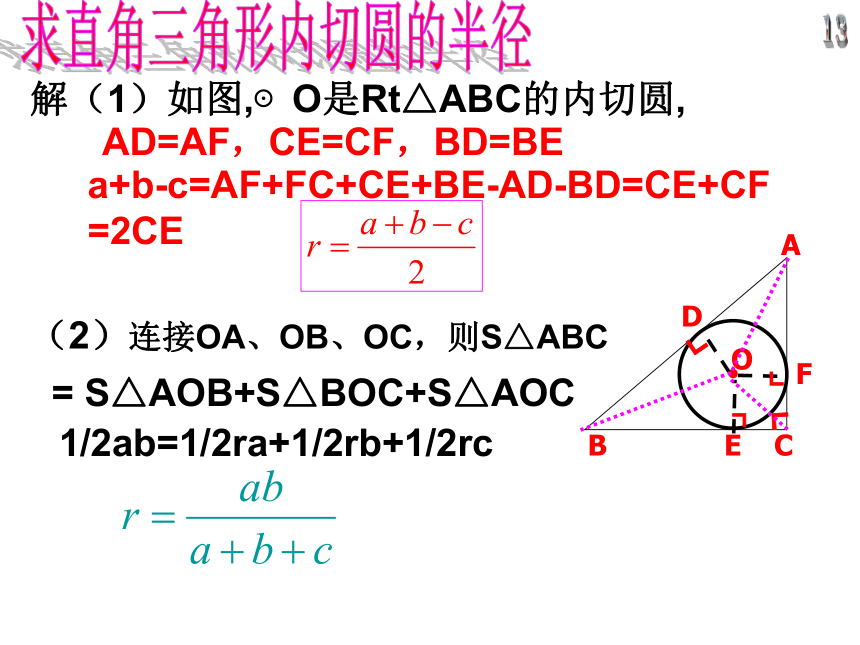
求直角三角形内切圆的半径AD=AF,CE=CF,BD=BEa+b-c=AF+FC+CE+BE-AD-BD=CE+CF
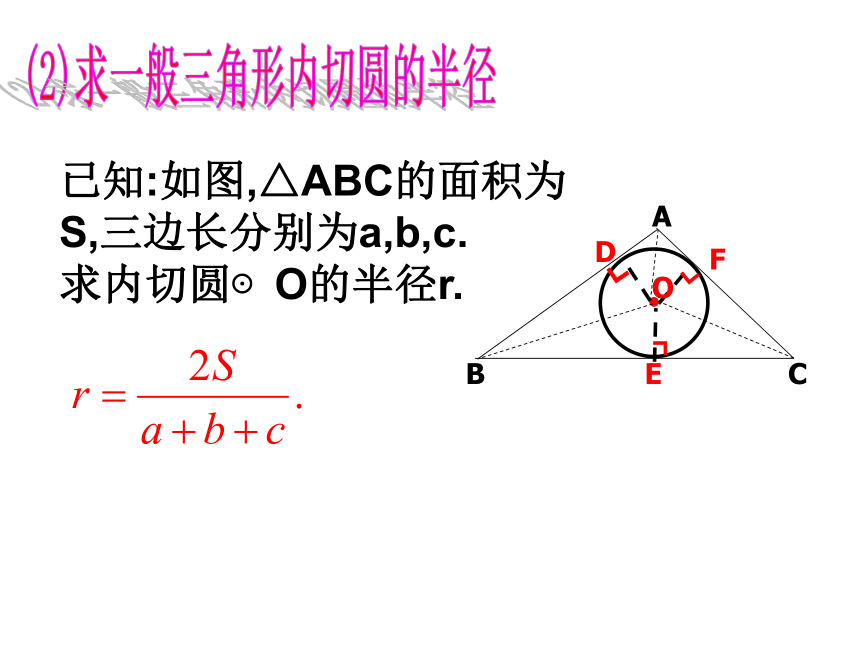
=2CE = S△AOB+S△BOC+S△AOC1/2ab=1/2ra+1/2rb+1/2rc(2)连接OA、OB、OC,则S△ABC(2)求一般三角形内切圆的半径已知:如图,△ABC的面积为S,三边长分别为a,b,c.
求内切圆⊙O的半径r.
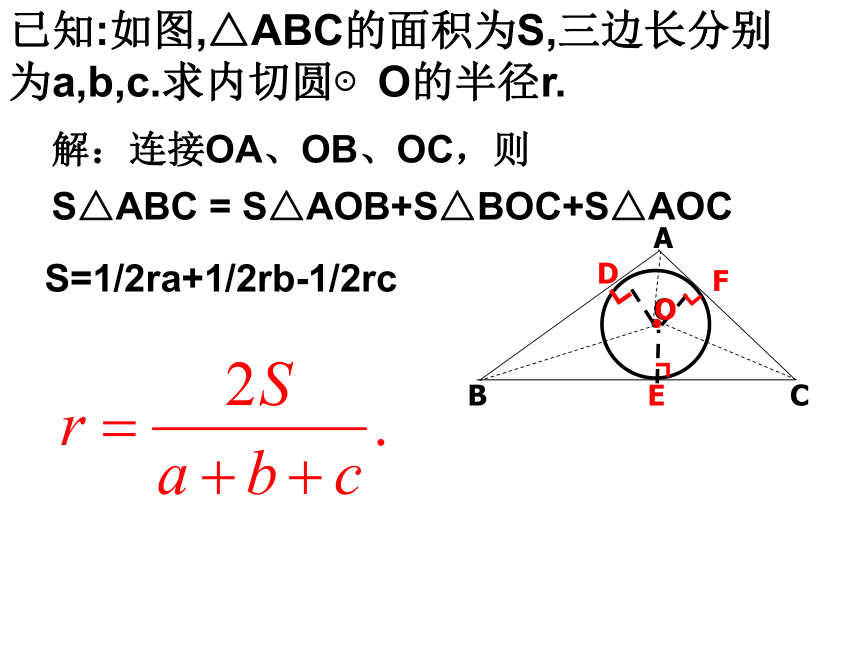
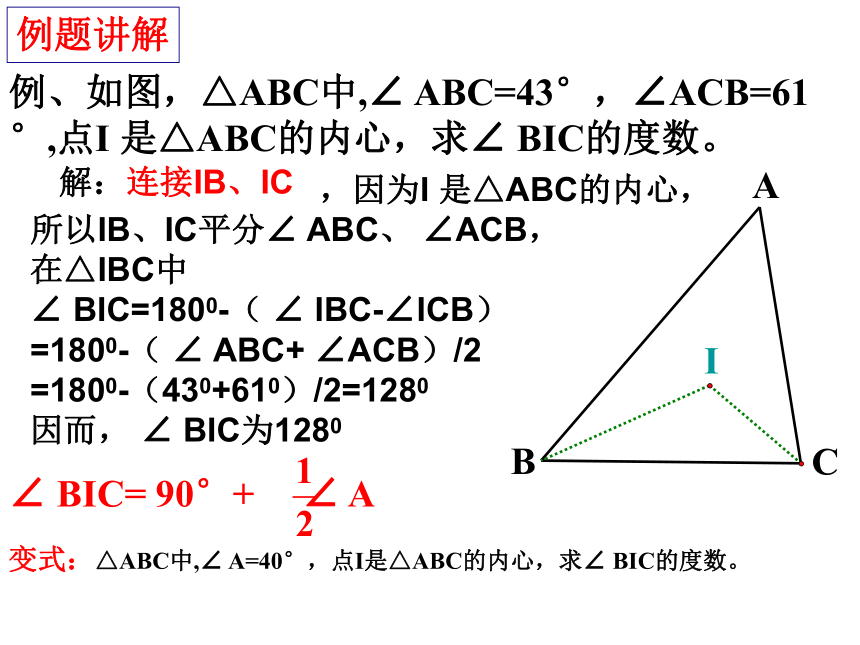
已知:如图,△ABC的面积为S,三边长分别为a,b,c.求内切圆⊙O的半径r.解:连接OA、OB、OC,则S△ABC = S△AOB+S△BOC+S△AOCS=1/2ra+1/2rb-1/2rc例、如图,△ABC中,∠ ABC=43°,∠ACB=61 °,点I 是△ABC的内心,求∠ BIC的度数。AICB例题讲解变式:△ABC中,∠ A=40°,点I是△ABC的内心,求∠ BIC的度数。∠ BIC= 90°+ ∠ A ,因为I 是△ABC的内心,
所以IB、IC平分∠ ABC、 ∠ACB,
在△IBC中
∠ BIC=1800-( ∠ IBC-∠ICB)
=1800-( ∠ ABC+ ∠ACB)/2
=1800-(430+610)/2=1280
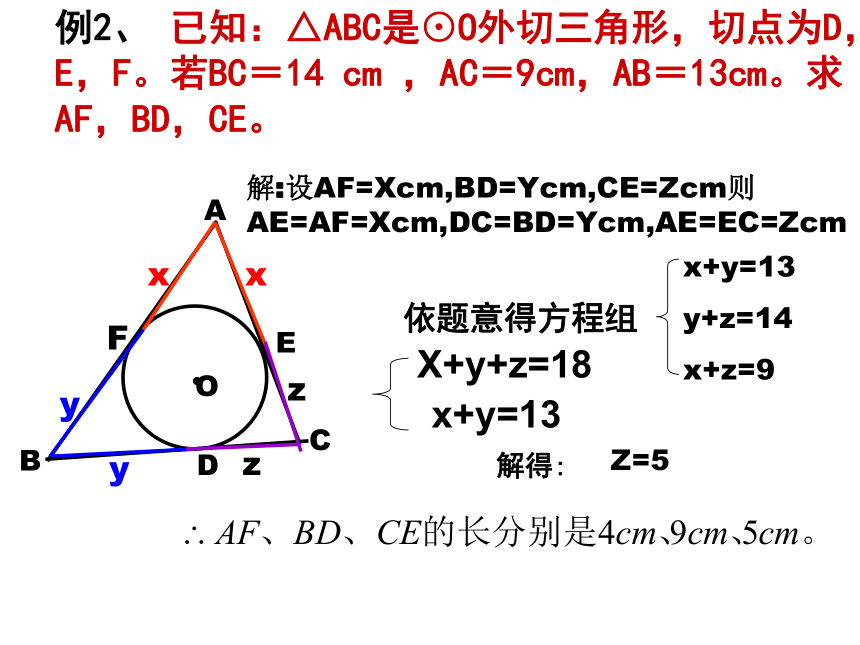
因而, ∠ BIC为1280解:连接IB、IC例2、 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。ABCDEFxxyyzz解:设AF=Xcm,BD=Ycm,CE=Zcm则AE=AF=Xcm,DC=BD=Ycm,AE=EC=Zcm依题意得方程组14
小练习1.边长为3、4、5的三角形的内切圆的半径为——2. 边长为5、5、6的三角形的内切圆的半径为——3. 已知:△ABC的面积S=4cm,周长等于10cm.求内切圆⊙O的半径r.1、如图, △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。x13﹣xx13﹣x9﹣x9﹣x例题分析2、△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积。(提示:设内心为O,连接OA、OB、OC。)OACBrrr若△ABC的内切圆半径为 r ,
周长为 l ,
则S△ABC= lr例题分析知识拓展一、直角三角形的外接圆与内切圆1.直角三角形外接圆的圆心(外心)在__________,半径为___________.abc斜边中点斜边的一半知识拓展3.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.14.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______.22cm2.直角三角形内切圆的圆心(内心)在__________,
半径r=___________.三角形内部回顾反思1.切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。回顾反思2.三角形的内切圆、内心、内心的性质1、如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
(A)50 (B) 52 (C)54 (D) 56课堂练习:B2、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.课堂练习 解:(1)OA⊥PA,OB⊥PB,PE⊥AB (2)设半径为r,则PA2=PDXPE
=PD(PD+2r)解得,OA=r=33、试一试:如图△ABC中,∠C=90?,AC=6,BC=8,三角形三边与⊙O均相切,切点分别是D、E、F,求⊙O的半径。 课堂练习AB2=AC2+BC2=62+82=100,AB=10证明:等边三角形的内心与外心重合,并且外接圆半径是内切圆半径的2倍 如图:等边△ABC中,I为圆心,
内切圆半径为r,外接圆半径为R
求证:①I为外心???②R=2r
证明①:连接AI、BI、CI,并延长;分别交对边于D、E、F
∵I是内心 ∴AD、CF、BF分别是△ABC的角平分线,
又△ABC是等边三角形,由等边三角形“三线合一”知
AD、BE、CF是△ABC的三条高,也是三角形的中线,
∴I是外心
②:由①知,BI=R,ID=r。在Rt△BID中∠IBD=1/2∠ABC=30°
∴ID=1/2IB,即R=2rP43习题25、6 第 2题解:设等边三角形ABC, 过点A作AD
垂直于BC 垂点为D,过B点做BE垂直于
AC 垂点为EAD与BE相交于点I ,
连接CI,并延长CI交AB于GF ∵AD和BE为高,而ABC是等边三角形 ∴BD=AE=1/2AC,∠CBE=∠DAC=30° ∠BEA=∠BDA=90°∴△BDI≌△AEI ∴BI=AFI,又∵BC=AC,CI=CI
∴△BIC≌△AIC ∴∠BCF=∠ACF,所以CF⊥AB ∵ID,IE,IF分别垂直于AB,BC,AC ,∴I就是△ABC的内心 BI=IC, BD=CD, DI=DI。 ∴△BDI≌△CDI , ∴BF=CF。同理可得 BI=CI。F 为△ABC的外心,且DI为内切圆半径,
BI为外接圆半径,又∵AD⊥BC,所以三角形BDI为直角三角形。又∠FBI=1/2∠ABC=30°, ∴ID=1/2BI 用全等三角形详解如图,圆O为△ABC的内切圆,切点为E、F、G,∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求圆O的半径r 解:连接OF,OE,则OFCE为边长为r的正方形 △OED ∽ △ ACD 故OE:AC=DE:DC r:4=(1-r):1 解得:r=4/5 P43习题25、6 第 4题解:连接BE, ∵点E为△ABC的内心, ∴∠BAD=∠DAC,
∠ABE=∠EBC. ∴BD=DC. ∵∠DAC与∠DBC都是
弧DC所对的圆周角, ∴∠DAC=∠DBC=∠BAD, ∵∠EBD=∠CBD+∠CBE,∠BED=∠ABE+∠BAD, ∴∠EBD=∠BED. ∴BD=ED. ∴BD=ED=DC.4.已知,如图,在△ABC中,点E是内心,延长AE交△ABC?的外接圆于点D,连接BD、DC、EC,求证:DB=DC=DE P43习题25、6 第 6题2、已知:在△ABC中,BC=14cm,AC=9cm,AB=13cm,BC,AC,AB分别与⊙O切于点D、E、F,求AF,BD和CE的长。P43习题25、6 第 8题分析:利用切线长定理可以得到AE=AF,BF=BD,CD=CE,因而可以设AF=xcm,BD=ycm,CE=zcm,根据BC=14cm,AC=9cm,AB=13cm即可得到一个关于x,y,z的方程组,即可求解. 解:设AF=xcm,BD=ycm,CE=zcm. ∵AF、AE是圆的切线∴AE=AF=xcm, 同理:BF=BD=ycm,CD=CE=zcm.根据题意得
解得,
.
即:AF=4cm,BD=9cm,CE=5cm. 如图,在△ABC中BC=14cm,AC=9cm,AB=13cm,内切圆⊙O分别和BC、AC、AB切于点D、E、F,求AF、BD、CE的长 x+y=13
x+z=9
y+z=14x=4,y=9,z=51.已知:两个同心圆PA、PB是大圆的两条切线,PC、PD是小圆的两条切线,A、B、C、D为切点。求证:AC=BD布置作业 3、以正方形ABCD的一边BC为直径的半圆上有一个动点K,过点K作半圆的切线EF,EF分别交AB、CD于点E、F,试问:四边形AEFD的周长是否会因K点的变动而变化?为什么?4、如图,在梯形ABCD中,AD//BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6,
求边AD、BC的长。5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,∠P=70°,求:△PEF的长和∠EOF的大小。
一块圆形的用料,并且使圆的面积尽可能大呢?ID思考三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆三角形的内心:三角形的内切圆的圆心叫做三角形的内心三角形的内心是三角形三
条角平分线的交点,它到
三角形三边的距离相等。概念介绍已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,三边长分别是a,b,c.求⊙O的半径r. Rt△的三边长与其内切圆半径间的关系探 究(1)求直角三角形内切圆的半径P43习题25、6 第 5题解(1)如图,⊙O是Rt△ABC的内切圆,13
求直角三角形内切圆的半径AD=AF,CE=CF,BD=BEa+b-c=AF+FC+CE+BE-AD-BD=CE+CF
=2CE = S△AOB+S△BOC+S△AOC1/2ab=1/2ra+1/2rb-1/2rc(2)连接OA、OB、OC,则S△ABC解(1)如图,⊙O是Rt△ABC的内切圆,13
求直角三角形内切圆的半径AD=AF,CE=CF,BD=BEa+b-c=AF+FC+CE+BE-AD-BD=CE+CF
=2CE = S△AOB+S△BOC+S△AOC1/2ab=1/2ra+1/2rb+1/2rc(2)连接OA、OB、OC,则S△ABC(2)求一般三角形内切圆的半径已知:如图,△ABC的面积为S,三边长分别为a,b,c.
求内切圆⊙O的半径r.
已知:如图,△ABC的面积为S,三边长分别为a,b,c.求内切圆⊙O的半径r.解:连接OA、OB、OC,则S△ABC = S△AOB+S△BOC+S△AOCS=1/2ra+1/2rb-1/2rc例、如图,△ABC中,∠ ABC=43°,∠ACB=61 °,点I 是△ABC的内心,求∠ BIC的度数。AICB例题讲解变式:△ABC中,∠ A=40°,点I是△ABC的内心,求∠ BIC的度数。∠ BIC= 90°+ ∠ A ,因为I 是△ABC的内心,
所以IB、IC平分∠ ABC、 ∠ACB,
在△IBC中
∠ BIC=1800-( ∠ IBC-∠ICB)
=1800-( ∠ ABC+ ∠ACB)/2
=1800-(430+610)/2=1280
因而, ∠ BIC为1280解:连接IB、IC例2、 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。ABCDEFxxyyzz解:设AF=Xcm,BD=Ycm,CE=Zcm则AE=AF=Xcm,DC=BD=Ycm,AE=EC=Zcm依题意得方程组14
小练习1.边长为3、4、5的三角形的内切圆的半径为——2. 边长为5、5、6的三角形的内切圆的半径为——3. 已知:△ABC的面积S=4cm,周长等于10cm.求内切圆⊙O的半径r.1、如图, △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长。x13﹣xx13﹣x9﹣x9﹣x例题分析2、△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积。(提示:设内心为O,连接OA、OB、OC。)OACBrrr若△ABC的内切圆半径为 r ,
周长为 l ,
则S△ABC= lr例题分析知识拓展一、直角三角形的外接圆与内切圆1.直角三角形外接圆的圆心(外心)在__________,半径为___________.abc斜边中点斜边的一半知识拓展3.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.14.直角三角形的外接圆半径为5cm,内切圆半径为1cm,则此三角形的周长是_______.22cm2.直角三角形内切圆的圆心(内心)在__________,
半径r=___________.三角形内部回顾反思1.切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。回顾反思2.三角形的内切圆、内心、内心的性质1、如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
(A)50 (B) 52 (C)54 (D) 56课堂练习:B2、已知,如图,PA、PB是⊙O的两条切线,A、B为切点.直线 OP 交 ⊙O 于点 D、E,交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长.课堂练习 解:(1)OA⊥PA,OB⊥PB,PE⊥AB (2)设半径为r,则PA2=PDXPE
=PD(PD+2r)解得,OA=r=33、试一试:如图△ABC中,∠C=90?,AC=6,BC=8,三角形三边与⊙O均相切,切点分别是D、E、F,求⊙O的半径。 课堂练习AB2=AC2+BC2=62+82=100,AB=10证明:等边三角形的内心与外心重合,并且外接圆半径是内切圆半径的2倍 如图:等边△ABC中,I为圆心,
内切圆半径为r,外接圆半径为R
求证:①I为外心???②R=2r
证明①:连接AI、BI、CI,并延长;分别交对边于D、E、F
∵I是内心 ∴AD、CF、BF分别是△ABC的角平分线,
又△ABC是等边三角形,由等边三角形“三线合一”知
AD、BE、CF是△ABC的三条高,也是三角形的中线,
∴I是外心
②:由①知,BI=R,ID=r。在Rt△BID中∠IBD=1/2∠ABC=30°
∴ID=1/2IB,即R=2rP43习题25、6 第 2题解:设等边三角形ABC, 过点A作AD
垂直于BC 垂点为D,过B点做BE垂直于
AC 垂点为EAD与BE相交于点I ,
连接CI,并延长CI交AB于GF ∵AD和BE为高,而ABC是等边三角形 ∴BD=AE=1/2AC,∠CBE=∠DAC=30° ∠BEA=∠BDA=90°∴△BDI≌△AEI ∴BI=AFI,又∵BC=AC,CI=CI
∴△BIC≌△AIC ∴∠BCF=∠ACF,所以CF⊥AB ∵ID,IE,IF分别垂直于AB,BC,AC ,∴I就是△ABC的内心 BI=IC, BD=CD, DI=DI。 ∴△BDI≌△CDI , ∴BF=CF。同理可得 BI=CI。F 为△ABC的外心,且DI为内切圆半径,
BI为外接圆半径,又∵AD⊥BC,所以三角形BDI为直角三角形。又∠FBI=1/2∠ABC=30°, ∴ID=1/2BI 用全等三角形详解如图,圆O为△ABC的内切圆,切点为E、F、G,∠C=90°,AO的延长线交BC于点D,AC=4,CD=1.求圆O的半径r 解:连接OF,OE,则OFCE为边长为r的正方形 △OED ∽ △ ACD 故OE:AC=DE:DC r:4=(1-r):1 解得:r=4/5 P43习题25、6 第 4题解:连接BE, ∵点E为△ABC的内心, ∴∠BAD=∠DAC,
∠ABE=∠EBC. ∴BD=DC. ∵∠DAC与∠DBC都是
弧DC所对的圆周角, ∴∠DAC=∠DBC=∠BAD, ∵∠EBD=∠CBD+∠CBE,∠BED=∠ABE+∠BAD, ∴∠EBD=∠BED. ∴BD=ED. ∴BD=ED=DC.4.已知,如图,在△ABC中,点E是内心,延长AE交△ABC?的外接圆于点D,连接BD、DC、EC,求证:DB=DC=DE P43习题25、6 第 6题2、已知:在△ABC中,BC=14cm,AC=9cm,AB=13cm,BC,AC,AB分别与⊙O切于点D、E、F,求AF,BD和CE的长。P43习题25、6 第 8题分析:利用切线长定理可以得到AE=AF,BF=BD,CD=CE,因而可以设AF=xcm,BD=ycm,CE=zcm,根据BC=14cm,AC=9cm,AB=13cm即可得到一个关于x,y,z的方程组,即可求解. 解:设AF=xcm,BD=ycm,CE=zcm. ∵AF、AE是圆的切线∴AE=AF=xcm, 同理:BF=BD=ycm,CD=CE=zcm.根据题意得
解得,
.
即:AF=4cm,BD=9cm,CE=5cm. 如图,在△ABC中BC=14cm,AC=9cm,AB=13cm,内切圆⊙O分别和BC、AC、AB切于点D、E、F,求AF、BD、CE的长 x+y=13
x+z=9
y+z=14x=4,y=9,z=51.已知:两个同心圆PA、PB是大圆的两条切线,PC、PD是小圆的两条切线,A、B、C、D为切点。求证:AC=BD布置作业 3、以正方形ABCD的一边BC为直径的半圆上有一个动点K,过点K作半圆的切线EF,EF分别交AB、CD于点E、F,试问:四边形AEFD的周长是否会因K点的变动而变化?为什么?4、如图,在梯形ABCD中,AD//BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6,
求边AD、BC的长。5、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,∠P=70°,求:△PEF的长和∠EOF的大小。
