北师大版六年级下册数学 正比例 (课件)
文档属性
| 名称 | 北师大版六年级下册数学 正比例 (课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
北师大版 小学数学 六年级下册
正 比 例
第一课时
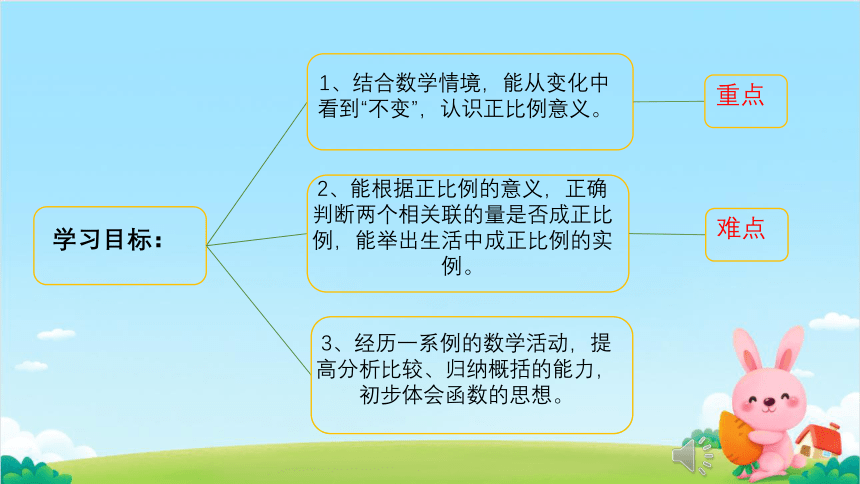
学习目标:
1、结合数学情境,能从变化中看到“不变”,认识正比例意义。
重点
2、能根据正比例的意义,正确判断两个相关联的量是否成正比例,能举出生活中成正比例的实例。
难点
3、经历一系例的数学活动,提高分析比较、归纳概括的能力,初步体会函数的思想。
同学们请看下面的这幅图,你会想到什么四字成语?请用前一节课学过的数学知识简单解释这种现象。
趣味引入
风起云涌
风起云飞
风云
变色
风吹草动
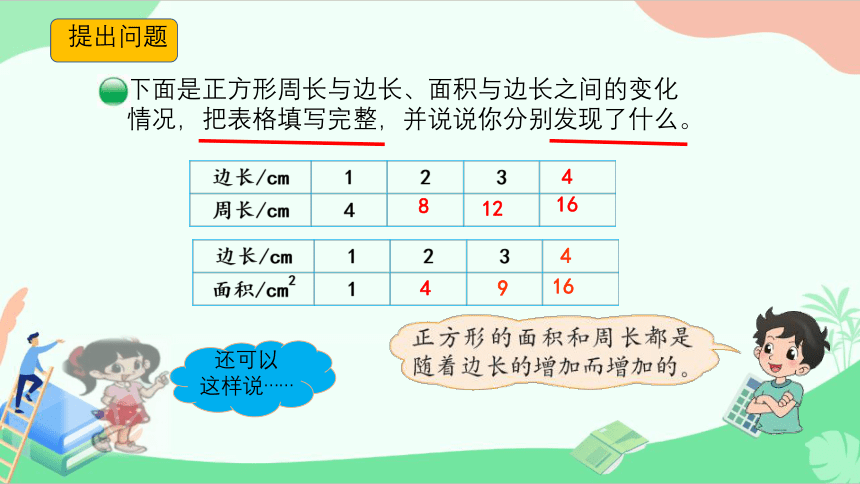
提出问题
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
8
12
4
16
4
4
16
9
还可以
这样说……
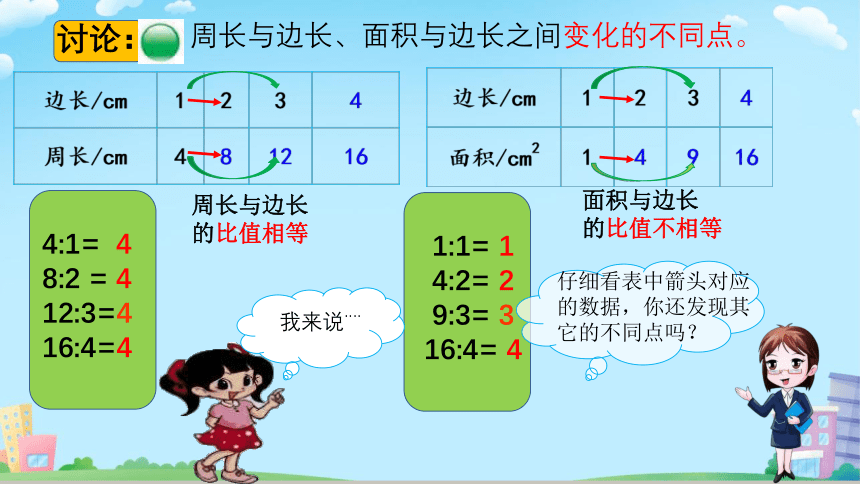
讨论:
周长与边长、面积与边长之间变化的不同点。
周长与边长的比值相等
面积与边长
的比值不相等
4:1= 4
8:2 = 4
12:3=4
16:4=4
1:1= 1
4:2= 2
9:3= 3
16:4= 4
仔细看表中箭头对应的数据,你还发现其它的不同点吗?
Q我来说¨¨
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
探究学习一
时 间:1 2 3 4 5 6 7 8
路 程:90 180 270 360 450 540 630 720
我发现:路程随着时间的变化而变化。
从左往右:路程随着时间的扩大而扩大。
从右往左:路程随着时间的缩小而缩小。
450
540
630
8
720
1、路程是如何随时间的变化而变化的?
2、任意写出三组路程和时间的比,并求出比值。
90:1 180:2 270:3
= = =
探究学习二
(一定)
90
90
90
3、你也可以通过看上面对应的箭头,说说每两对数字可组成的比例有哪些?同桌互相说说,尽量多说。
如:1:2=90:180、1:90=2:180
路程和时间是两种相关联的量,
时间变化,所行驶的路程也随着变化,
而且路程与时间的比值(也就是速度)一定,
我们就说路程和时间成正比例。
请根据下表,说说当速度不变时,路程和时间的变化规律。
探究学习三
周长随着边长的变化而变化。
周长与边长的
比值相等。(一定)
面积随着边长的变化而变化。
面积与边长
的比值不一定。
正方形的周长与
边长成正比例。
正方形的面积与边长不成正比例
4:1= 4
8:2 = 4
12:3=4
16:4=4
1:1= 1
4:2= 2
9:3= 3
16:4= 4
新课检验
第一个问题中,正方形的周长与边长,面积与边长成正比例吗?
课堂小结:
填一填:
两种( )量,一种量变化,另一种量也( ),如果这两种量中( )的两个数的( )一定,这两种量就叫做成正比例的量,它们的关系叫做( )关系。
相关联
随着变化
相对应
比值
正比例
这是同学们参加研学的人数与钱数情况统计如下表,说说人数与钱数的关系。
表中有( ) 和( )两个量,( )变化,( )也随着变化,而且钱数与人数的比值一定,
我们就说人数与钱数成正比例。
人数
人数
钱数
一、学以致用:
钱数
根据下表,仿照课本p41,说一说
巩固练习
⑴说一说竿影的长与竹竿的高的变化关系。
⑵写出竿影的长与竹竿的高的比,你有什么发现?
⑶竹竿的高与竿影的长是不是成正比例?说明理由。
⑴说一说竿影的长与竹竿的高的变化关系。
答:竿影的长随着竹竿的高的增长而增长。
0.4:1=0.4 0.8:2=0.4 1.2:3=0.4 1.6:4=0.4
2.4:6=0.4 3.2:8=0.4
我发现:比值都是0.4
答:竹竿的高与竿影的长成正比例。因为竿影的长随着竹竿的高的变化而变化,而且竿影的长与竹竿的高的比值一定。
(2)写出竿影的长与竹竿对应的高的比, 你有什么发现?
(3)竹竿的高与竿影的长是不是成正比例? 说明理由。
1.学校科学小组在同一时间、同一地点进行
观察实验,测得竹竿的高与竿影的长如下表。
二、练一练
我 还发现…
1、长方形的长一定,面积与宽成正比例。( )
2、汽车行驶的速度一定,路程与时间成正比例。( )
3、订阅《广东第一课堂》的钱数和人数成正比例。( )
4、做早操时,如果每列人数相等,那么总人数和列数成正比例。( )
5、工作总量与工作时间成正比例。( )
三、明辨是非
判断下面的对错,对的在括号里打√,错的打×
×
√
√
√
√
200
7
根据x、y成正比例,填写表中空格
100
四、拓展练习:
五、趣味 乐园
边听音乐边观察表格,听完音乐后
具体说出下表中有哪些量是成正比例的量。
通过这节课的学习,你学到了什么?还有哪些疑惑?
布置作业:(用作业纸打印给学生)
*必做题、文具店卖出书包的情况如下表:
1、说一说总价和数量的变化关系。
2、写出三组总价与数量相对应的比,并求出比值,
你发现了什么?
3、总价与数量是成正比例吗? 说明理由
选做题、举例说说小学阶段所学过的数学公式中,当什么量一定时,另两个量成正比例。 ( 每人写2个例子)
如:当圆柱的底面积一定时,体积和高成正比例
谢谢大家的聆听!
北师大版 小学数学 六年级下册
正 比 例
第一课时
学习目标:
1、结合数学情境,能从变化中看到“不变”,认识正比例意义。
重点
2、能根据正比例的意义,正确判断两个相关联的量是否成正比例,能举出生活中成正比例的实例。
难点
3、经历一系例的数学活动,提高分析比较、归纳概括的能力,初步体会函数的思想。
同学们请看下面的这幅图,你会想到什么四字成语?请用前一节课学过的数学知识简单解释这种现象。
趣味引入
风起云涌
风起云飞
风云
变色
风吹草动
提出问题
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整,并说说你分别发现了什么。
8
12
4
16
4
4
16
9
还可以
这样说……
讨论:
周长与边长、面积与边长之间变化的不同点。
周长与边长的比值相等
面积与边长
的比值不相等
4:1= 4
8:2 = 4
12:3=4
16:4=4
1:1= 1
4:2= 2
9:3= 3
16:4= 4
仔细看表中箭头对应的数据,你还发现其它的不同点吗?
Q我来说¨¨
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么?
探究学习一
时 间:1 2 3 4 5 6 7 8
路 程:90 180 270 360 450 540 630 720
我发现:路程随着时间的变化而变化。
从左往右:路程随着时间的扩大而扩大。
从右往左:路程随着时间的缩小而缩小。
450
540
630
8
720
1、路程是如何随时间的变化而变化的?
2、任意写出三组路程和时间的比,并求出比值。
90:1 180:2 270:3
= = =
探究学习二
(一定)
90
90
90
3、你也可以通过看上面对应的箭头,说说每两对数字可组成的比例有哪些?同桌互相说说,尽量多说。
如:1:2=90:180、1:90=2:180
路程和时间是两种相关联的量,
时间变化,所行驶的路程也随着变化,
而且路程与时间的比值(也就是速度)一定,
我们就说路程和时间成正比例。
请根据下表,说说当速度不变时,路程和时间的变化规律。
探究学习三
周长随着边长的变化而变化。
周长与边长的
比值相等。(一定)
面积随着边长的变化而变化。
面积与边长
的比值不一定。
正方形的周长与
边长成正比例。
正方形的面积与边长不成正比例
4:1= 4
8:2 = 4
12:3=4
16:4=4
1:1= 1
4:2= 2
9:3= 3
16:4= 4
新课检验
第一个问题中,正方形的周长与边长,面积与边长成正比例吗?
课堂小结:
填一填:
两种( )量,一种量变化,另一种量也( ),如果这两种量中( )的两个数的( )一定,这两种量就叫做成正比例的量,它们的关系叫做( )关系。
相关联
随着变化
相对应
比值
正比例
这是同学们参加研学的人数与钱数情况统计如下表,说说人数与钱数的关系。
表中有( ) 和( )两个量,( )变化,( )也随着变化,而且钱数与人数的比值一定,
我们就说人数与钱数成正比例。
人数
人数
钱数
一、学以致用:
钱数
根据下表,仿照课本p41,说一说
巩固练习
⑴说一说竿影的长与竹竿的高的变化关系。
⑵写出竿影的长与竹竿的高的比,你有什么发现?
⑶竹竿的高与竿影的长是不是成正比例?说明理由。
⑴说一说竿影的长与竹竿的高的变化关系。
答:竿影的长随着竹竿的高的增长而增长。
0.4:1=0.4 0.8:2=0.4 1.2:3=0.4 1.6:4=0.4
2.4:6=0.4 3.2:8=0.4
我发现:比值都是0.4
答:竹竿的高与竿影的长成正比例。因为竿影的长随着竹竿的高的变化而变化,而且竿影的长与竹竿的高的比值一定。
(2)写出竿影的长与竹竿对应的高的比, 你有什么发现?
(3)竹竿的高与竿影的长是不是成正比例? 说明理由。
1.学校科学小组在同一时间、同一地点进行
观察实验,测得竹竿的高与竿影的长如下表。
二、练一练
我 还发现…
1、长方形的长一定,面积与宽成正比例。( )
2、汽车行驶的速度一定,路程与时间成正比例。( )
3、订阅《广东第一课堂》的钱数和人数成正比例。( )
4、做早操时,如果每列人数相等,那么总人数和列数成正比例。( )
5、工作总量与工作时间成正比例。( )
三、明辨是非
判断下面的对错,对的在括号里打√,错的打×
×
√
√
√
√
200
7
根据x、y成正比例,填写表中空格
100
四、拓展练习:
五、趣味 乐园
边听音乐边观察表格,听完音乐后
具体说出下表中有哪些量是成正比例的量。
通过这节课的学习,你学到了什么?还有哪些疑惑?
布置作业:(用作业纸打印给学生)
*必做题、文具店卖出书包的情况如下表:
1、说一说总价和数量的变化关系。
2、写出三组总价与数量相对应的比,并求出比值,
你发现了什么?
3、总价与数量是成正比例吗? 说明理由
选做题、举例说说小学阶段所学过的数学公式中,当什么量一定时,另两个量成正比例。 ( 每人写2个例子)
如:当圆柱的底面积一定时,体积和高成正比例
谢谢大家的聆听!
