人教版 六年级数学下册《比例的基本性质》课件(共19张PPT)
文档属性
| 名称 | 人教版 六年级数学下册《比例的基本性质》课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 777.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 11:01:54 | ||
图片预览


文档简介
(共19张PPT)
比例的基本性质
什么叫做比例?
表示两个比相等的式子叫做比例。
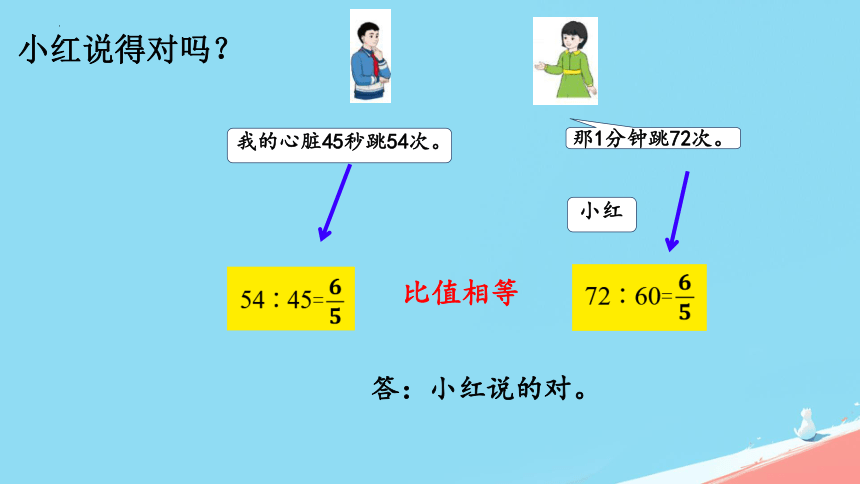
小红说得对吗?
那1分钟跳72次。
我的心脏45秒跳54次。
小红
答:小红说的对。
比值相等
2.4∶1.6 和 60∶ 40
=
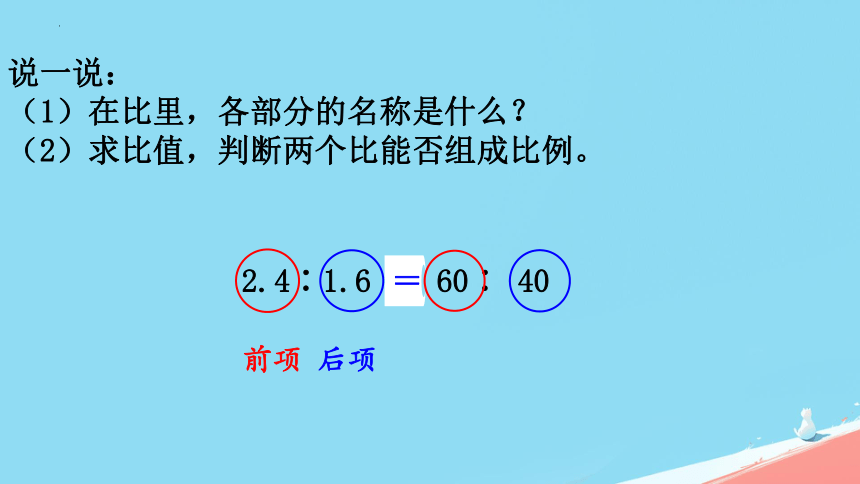
说一说:
(1)在比里,各部分的名称是什么?
(2)求比值,判断两个比能否组成比例。
前项
后项
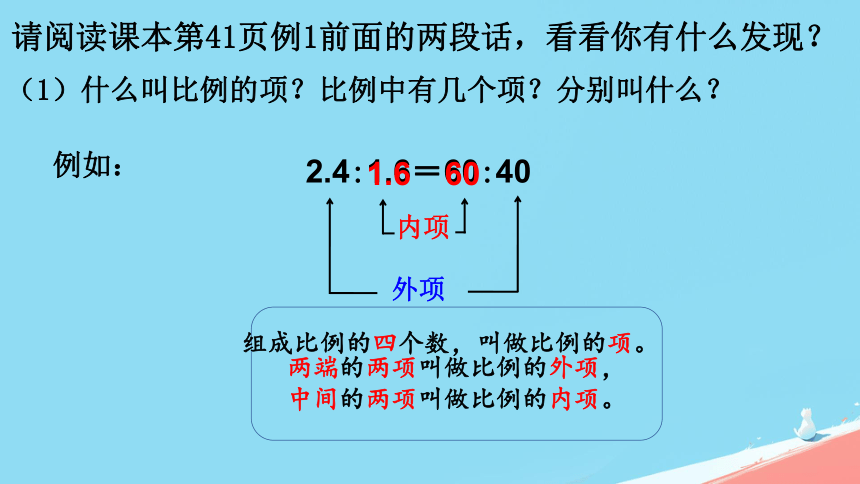
请阅读课本第41页例1前面的两段话,看看你有什么发现?
(1)什么叫比例的项?比例中有几个项?分别叫什么?
例如:
2.4:1.6=60:40
1.6
60
内项
外项
两端的两项叫做比例的外项,
中间的两项叫做比例的内项。
组成比例的四个数,叫做比例的项。
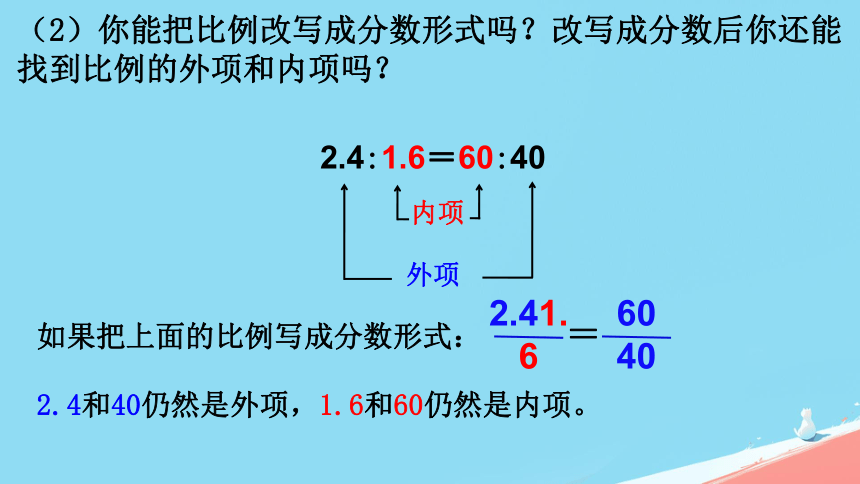
(2)你能把比例改写成分数形式吗?改写成分数后你还能找到比例的外项和内项吗?
如果把上面的比例写成分数形式:
2.4和40仍然是外项,1.6和60仍然是内项。
2.4:1.6=60:40
内项
外项
2.41.6
6040
=
( )
35
9 15
=
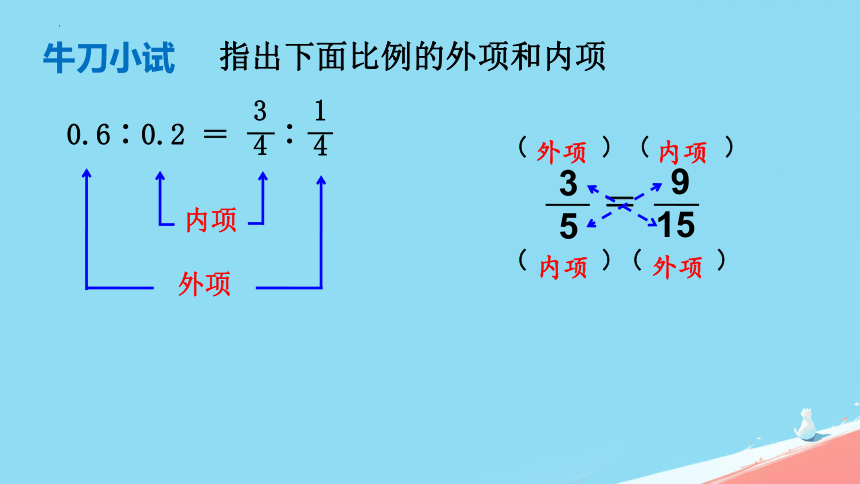
牛刀小试
指出下面比例的外项和内项
0.6∶0.2 = ∶
( )
内项
( )
( )
外项
外项
内项
34
14
外项
内项
( )
( )
把下面比例改写成分数形式,并找出它的外项和内项。
6 : 10 = 9 : 15 0.2 : 2.5 = 4 : 50
( )
内项
( )
外项
外项
内项
( )
内项
( )
( )
( )
外项
外项
内项
6 10
9 15
=
0.22.5
4 50
=
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(1) 2.4:1.6=60:40
2.4×40=96
1.6×60=96
观察计算结果,你有什么发现吗?
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(2) =
9 15
35
3×15= 45
5×9= 45
先计算,再观察,看看有什么发现?
你能举一个例子,验证你的发现吗?
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
你能用字母表示这个性质吗?
如果 a:b=c:d(b、d≠0)
ad = bc
或
交叉相乘积相等
ab
cd
=
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(1)6:3和8:5
6×5=30
3×8=24
不能组成比例
(2)0.2:2.5和4:50
0.2×50=10
2.5×4=10
可以组成比例
做一做
0.2:2.5=4:50
(3) 和
(4)1.2: 和 : 5
可以组成比例
不能组成比例
13
16
∶
12
14
∶
1 12
13
14
×
=
12
16
×
=
1 12
13
16
∶
12
14
∶
=
34
45
1.2×5= 6
34
45
×
=
35
(2)0.2 : 2.5 = 4 : ( )
应用比例的基本性质填空
(1)6:3 =( ):5
10
50
(3) :( ) = :
13
12
14
( ) 8
54
(4)
=
16
10
(1)在比例里,两个内项的积是18,其中一个外项是2,另一个外项是( )。
9
填空题:
(1)两块水稻田的产量与面积之比,是否可以组成比例?
3.75:0.5 和 6:0.8
3.75×0.8=3
0.5×6=3
答:两块水稻田的产量与面积之比,可以组成比例。
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。
3.75:0.5=6:0.8
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。
(2)如果可以组成比例,指出比例的内项和外项。
3.75 : 0.5 = 6 : 0.8
内项
外项
答:比例的内项是0.5和6,比例的外项是3.75和0.8。
张师傅昨天6小时做了72个零件,今天8小时做了96个零件,写出张师傅昨天和今天所做零件个数的比和所用时间的比。这两个比能组成比例吗?为什么?
零件个数比是 72:96
所用时间比是 6:8
假设72:96=6:8
内项积96×6=576
外项积72×8=576
所以72:96和6:8能组成比例
72:96=6:8
比和比例的区别与联系
表示两个数相除
表示两个比相等
2项
4项
比是一个除法算式
比例是一个等式
这节课你们都学会了哪些知识?
比例的各部分名称及基本性质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
判断比例是否成立的方法:
①看比值是否相等。
②运用比例的基本性质判断。
比例的基本性质
什么叫做比例?
表示两个比相等的式子叫做比例。
小红说得对吗?
那1分钟跳72次。
我的心脏45秒跳54次。
小红
答:小红说的对。
比值相等
2.4∶1.6 和 60∶ 40
=
说一说:
(1)在比里,各部分的名称是什么?
(2)求比值,判断两个比能否组成比例。
前项
后项
请阅读课本第41页例1前面的两段话,看看你有什么发现?
(1)什么叫比例的项?比例中有几个项?分别叫什么?
例如:
2.4:1.6=60:40
1.6
60
内项
外项
两端的两项叫做比例的外项,
中间的两项叫做比例的内项。
组成比例的四个数,叫做比例的项。
(2)你能把比例改写成分数形式吗?改写成分数后你还能找到比例的外项和内项吗?
如果把上面的比例写成分数形式:
2.4和40仍然是外项,1.6和60仍然是内项。
2.4:1.6=60:40
内项
外项
2.41.6
6040
=
( )
35
9 15
=
牛刀小试
指出下面比例的外项和内项
0.6∶0.2 = ∶
( )
内项
( )
( )
外项
外项
内项
34
14
外项
内项
( )
( )
把下面比例改写成分数形式,并找出它的外项和内项。
6 : 10 = 9 : 15 0.2 : 2.5 = 4 : 50
( )
内项
( )
外项
外项
内项
( )
内项
( )
( )
( )
外项
外项
内项
6 10
9 15
=
0.22.5
4 50
=
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(1) 2.4:1.6=60:40
2.4×40=96
1.6×60=96
观察计算结果,你有什么发现吗?
计算下面比例中两个外项的积和两个内项的积。
比较一下,你能发现什么?
(2) =
9 15
35
3×15= 45
5×9= 45
先计算,再观察,看看有什么发现?
你能举一个例子,验证你的发现吗?
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
你能用字母表示这个性质吗?
如果 a:b=c:d(b、d≠0)
ad = bc
或
交叉相乘积相等
ab
cd
=
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
(1)6:3和8:5
6×5=30
3×8=24
不能组成比例
(2)0.2:2.5和4:50
0.2×50=10
2.5×4=10
可以组成比例
做一做
0.2:2.5=4:50
(3) 和
(4)1.2: 和 : 5
可以组成比例
不能组成比例
13
16
∶
12
14
∶
1 12
13
14
×
=
12
16
×
=
1 12
13
16
∶
12
14
∶
=
34
45
1.2×5= 6
34
45
×
=
35
(2)0.2 : 2.5 = 4 : ( )
应用比例的基本性质填空
(1)6:3 =( ):5
10
50
(3) :( ) = :
13
12
14
( ) 8
54
(4)
=
16
10
(1)在比例里,两个内项的积是18,其中一个外项是2,另一个外项是( )。
9
填空题:
(1)两块水稻田的产量与面积之比,是否可以组成比例?
3.75:0.5 和 6:0.8
3.75×0.8=3
0.5×6=3
答:两块水稻田的产量与面积之比,可以组成比例。
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。
3.75:0.5=6:0.8
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。
(2)如果可以组成比例,指出比例的内项和外项。
3.75 : 0.5 = 6 : 0.8
内项
外项
答:比例的内项是0.5和6,比例的外项是3.75和0.8。
张师傅昨天6小时做了72个零件,今天8小时做了96个零件,写出张师傅昨天和今天所做零件个数的比和所用时间的比。这两个比能组成比例吗?为什么?
零件个数比是 72:96
所用时间比是 6:8
假设72:96=6:8
内项积96×6=576
外项积72×8=576
所以72:96和6:8能组成比例
72:96=6:8
比和比例的区别与联系
表示两个数相除
表示两个比相等
2项
4项
比是一个除法算式
比例是一个等式
这节课你们都学会了哪些知识?
比例的各部分名称及基本性质
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
判断比例是否成立的方法:
①看比值是否相等。
②运用比例的基本性质判断。
