23.3 相似三角形(第6课时)相似三角形的应用习题课件(22张PPT)2023-2024学年华东师大版数学九年级上册
文档属性
| 名称 | 23.3 相似三角形(第6课时)相似三角形的应用习题课件(22张PPT)2023-2024学年华东师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 14:01:19 | ||
图片预览






文档简介
(共22张PPT)
23.3 相似三角形
课时6 相似三角形的应用
过基础 教材必备知识精练
知识点1 利用相似三角形的性质测量
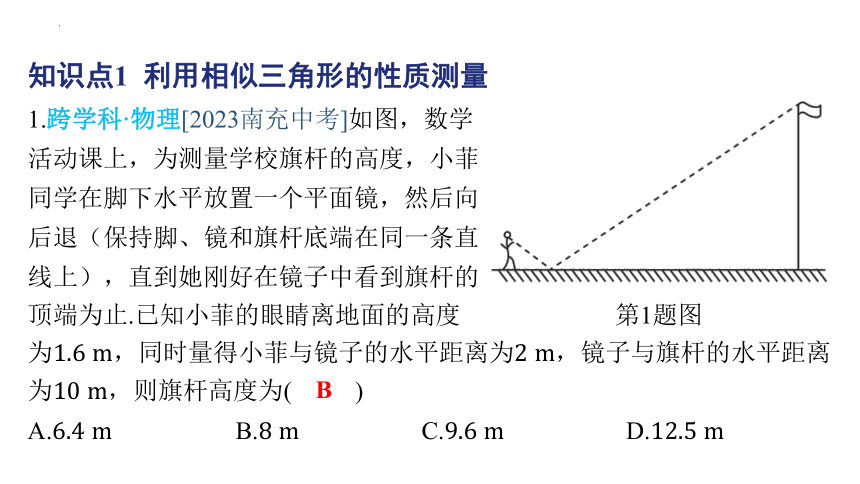
第1题图
1.跨学科·物理[2023南充中考]如图,数学
活动课上,为测量学校旗杆的高度,小菲
同学在脚下水平放置一个平面镜,然后向
后退(保持脚、镜和旗杆底端在同一条直
线上),直到她刚好在镜子中看到旗杆的
顶端为止.已知小菲的眼睛离地面的高度
B
A. B. C. D.
为,同时量得小菲与镜子的水平距离为 ,镜子与旗杆的水平距离
为 ,则旗杆高度为( )
【解析】 如图,,, ,又
(反射角=入射角,等角的余角相等),
,,, .
第2题图
2.[2024漳州期中]图1是装了液体的高脚杯示意图
(数据如图),用去一部分液体后如图2所示,此时液
面 ( )
C
A. B. C. D.
【解析】 根据“相似三角形对应高的比等于相似比”可
知,即, .
3.[2022十堰中考]如图,某零件的外径为 ,用一个交
叉卡钳(两条尺长和 相等)可测量零件的内孔直径
.若,且量得 ,则零
件的厚度为____ .
0.5
【解析】 , ,
, ,
. 该零件的外径为, 零件的厚度 为
.
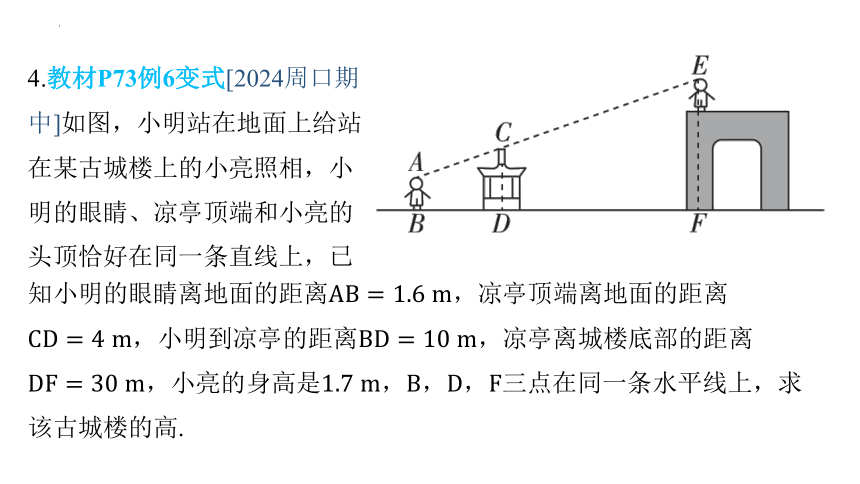
4.教材P73例6变式[2024周口期
中]如图,小明站在地面上给站
在某古城楼上的小亮照相,小
明的眼睛、凉亭顶端和小亮的
头顶恰好在同一条直线上,已
知小明的眼睛离地面的距离 ,凉亭顶端离地面的距离
,小明到凉亭的距离 ,凉亭离城楼底部的距离
,小亮的身高是,,, 三点在同一条水平线上,求
该古城楼的高.
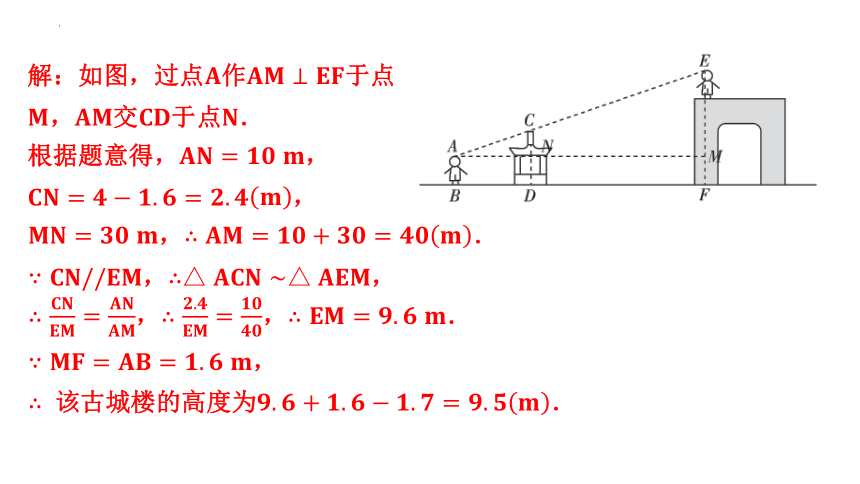
解:如图,过点作 于点
,交于点 .
根据题意得, ,
,
, .
, ,
,, .
,
该古城楼的高度为 .
知识点2 利用相似三角形的性质证明等积式
5.[2023福州一中(初中部)月考]如图,在中,点在 边上,连
接,点在边上,过点作,交于点,过点作 ,
交于点 ,则下列式子一定正确的是( )
C
A. B. C. D.
【解析】 ,, ,故选项A中的式子错
误.,,, 只有当 时,
才成立,此时,故选项B中的式子不一定正确. ,
,, ,故选项C中的式子一定正确.只有当
时, 才成立,故选项D中的式子不一定正确.
6.如图,在四边形中, ,
过点作对角线的垂线,分别交, 于点
,,求证: .
证明: , ,
,, .
, ,
, ,
, .
23.3 相似三角形
课时6 相似三角形的应用
过能力 学科关键能力构建
1.新趋势·数学文化[2024杭州西
湖区月考]我国古代数学著作
《九章算术》中记载了一个问题:
“今有邑方不知大小,各开中门,
出北门三十步有木,出西门七百
五十步见木,问:邑方几何?”
A
A.300步 B.275步 C.285步 D.315步
其大意是:如图,一座正方形城池,为北门中点,从点 往正北方向走
30步到处有一树木,为西门中点,从点往正西方向走750步到 处正好
看到 处的树木,则正方形城池的边长为 ( )
【解析】 如图,设正方形城池的边长为步,则 步
,,又 ,
,,, .
2.[2024长治期中]如图,在某小区内的一段小
路上,有一个儿童在2号楼一侧的 处玩耍,
此时有一辆小轿车从2号楼另一侧的 处驶来.
已知于点,点在 延长线上,
于点,与交于点 ,
,, ,
,则汽车从处前行的距离
_____时,才能发现 处的儿童.
5.75
【解析】 在中,, ,
, ,
,,,.在
中,,, ,
, 汽车从处前行时,才能发现 处
的儿童.
3.[2023攀枝花中考]拜寺口双塔,分为
东西两塔,位于宁夏回族自治区银川市
贺兰县拜寺口内,是保存最为完整的西
夏佛塔,已有近1 000年历史,是中国佛塔建筑史上不可多得的艺术珍品.
某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的
原理,来测量东塔的高度.如图,东塔的高度为,选取与塔底 在同一水
平地面上的,两点,分别垂直地面竖立两根高为的标杆和 ,
两标杆间隔为,并且东塔、标杆和 在同一竖直平面内.从
标杆后退到处(即),从处观察点,,, 三点
在同一条直线上;从标杆后退到处(即),从 处观察
点,,,三点也在同一条直线上,且,,,, 在同一条直
线上.请你根据以上测量数据,帮助兴趣小组求出东塔 的高度.
解:设 ,则
.
,, ,
,, .
同理,可证, ,
,,解得 .
经检验,是原方程的解, ,
, 东塔的高度为 .
素养提升
4.推理能力[2023绍兴期中]如图,在正方形
中,,分别是边,上的点, ,垂
足是点 .
(1)求证: .
证明: 四边形 是正方形,
, .
, , .
又 , .
在和中,
, .
【解析】 解题思路:利用正方形的四条边相等及每个角为 证明
;
(2)连接,,若,求证: .
四边形是正方形,,, ,
.
, .
又,, .
由(1)得,, ,
, .
【解析】 解题思路:先利用正方形的对边平行得到相等的角,再结合题
中条件证明 ,得到成比例线段,最后结合(1)中全等三
角形的性质(边相等)即可证得 .
23.3 相似三角形
课时6 相似三角形的应用
过基础 教材必备知识精练
知识点1 利用相似三角形的性质测量
第1题图
1.跨学科·物理[2023南充中考]如图,数学
活动课上,为测量学校旗杆的高度,小菲
同学在脚下水平放置一个平面镜,然后向
后退(保持脚、镜和旗杆底端在同一条直
线上),直到她刚好在镜子中看到旗杆的
顶端为止.已知小菲的眼睛离地面的高度
B
A. B. C. D.
为,同时量得小菲与镜子的水平距离为 ,镜子与旗杆的水平距离
为 ,则旗杆高度为( )
【解析】 如图,,, ,又
(反射角=入射角,等角的余角相等),
,,, .
第2题图
2.[2024漳州期中]图1是装了液体的高脚杯示意图
(数据如图),用去一部分液体后如图2所示,此时液
面 ( )
C
A. B. C. D.
【解析】 根据“相似三角形对应高的比等于相似比”可
知,即, .
3.[2022十堰中考]如图,某零件的外径为 ,用一个交
叉卡钳(两条尺长和 相等)可测量零件的内孔直径
.若,且量得 ,则零
件的厚度为____ .
0.5
【解析】 , ,
, ,
. 该零件的外径为, 零件的厚度 为
.
4.教材P73例6变式[2024周口期
中]如图,小明站在地面上给站
在某古城楼上的小亮照相,小
明的眼睛、凉亭顶端和小亮的
头顶恰好在同一条直线上,已
知小明的眼睛离地面的距离 ,凉亭顶端离地面的距离
,小明到凉亭的距离 ,凉亭离城楼底部的距离
,小亮的身高是,,, 三点在同一条水平线上,求
该古城楼的高.
解:如图,过点作 于点
,交于点 .
根据题意得, ,
,
, .
, ,
,, .
,
该古城楼的高度为 .
知识点2 利用相似三角形的性质证明等积式
5.[2023福州一中(初中部)月考]如图,在中,点在 边上,连
接,点在边上,过点作,交于点,过点作 ,
交于点 ,则下列式子一定正确的是( )
C
A. B. C. D.
【解析】 ,, ,故选项A中的式子错
误.,,, 只有当 时,
才成立,此时,故选项B中的式子不一定正确. ,
,, ,故选项C中的式子一定正确.只有当
时, 才成立,故选项D中的式子不一定正确.
6.如图,在四边形中, ,
过点作对角线的垂线,分别交, 于点
,,求证: .
证明: , ,
,, .
, ,
, ,
, .
23.3 相似三角形
课时6 相似三角形的应用
过能力 学科关键能力构建
1.新趋势·数学文化[2024杭州西
湖区月考]我国古代数学著作
《九章算术》中记载了一个问题:
“今有邑方不知大小,各开中门,
出北门三十步有木,出西门七百
五十步见木,问:邑方几何?”
A
A.300步 B.275步 C.285步 D.315步
其大意是:如图,一座正方形城池,为北门中点,从点 往正北方向走
30步到处有一树木,为西门中点,从点往正西方向走750步到 处正好
看到 处的树木,则正方形城池的边长为 ( )
【解析】 如图,设正方形城池的边长为步,则 步
,,又 ,
,,, .
2.[2024长治期中]如图,在某小区内的一段小
路上,有一个儿童在2号楼一侧的 处玩耍,
此时有一辆小轿车从2号楼另一侧的 处驶来.
已知于点,点在 延长线上,
于点,与交于点 ,
,, ,
,则汽车从处前行的距离
_____时,才能发现 处的儿童.
5.75
【解析】 在中,, ,
, ,
,,,.在
中,,, ,
, 汽车从处前行时,才能发现 处
的儿童.
3.[2023攀枝花中考]拜寺口双塔,分为
东西两塔,位于宁夏回族自治区银川市
贺兰县拜寺口内,是保存最为完整的西
夏佛塔,已有近1 000年历史,是中国佛塔建筑史上不可多得的艺术珍品.
某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的
原理,来测量东塔的高度.如图,东塔的高度为,选取与塔底 在同一水
平地面上的,两点,分别垂直地面竖立两根高为的标杆和 ,
两标杆间隔为,并且东塔、标杆和 在同一竖直平面内.从
标杆后退到处(即),从处观察点,,, 三点
在同一条直线上;从标杆后退到处(即),从 处观察
点,,,三点也在同一条直线上,且,,,, 在同一条直
线上.请你根据以上测量数据,帮助兴趣小组求出东塔 的高度.
解:设 ,则
.
,, ,
,, .
同理,可证, ,
,,解得 .
经检验,是原方程的解, ,
, 东塔的高度为 .
素养提升
4.推理能力[2023绍兴期中]如图,在正方形
中,,分别是边,上的点, ,垂
足是点 .
(1)求证: .
证明: 四边形 是正方形,
, .
, , .
又 , .
在和中,
, .
【解析】 解题思路:利用正方形的四条边相等及每个角为 证明
;
(2)连接,,若,求证: .
四边形是正方形,,, ,
.
, .
又,, .
由(1)得,, ,
, .
【解析】 解题思路:先利用正方形的对边平行得到相等的角,再结合题
中条件证明 ,得到成比例线段,最后结合(1)中全等三
角形的性质(边相等)即可证得 .
