第24章 解直角三角形易错疑难集训习题课件(20张PPT)2023-2024学年华东师大版数学九年级上册
文档属性
| 名称 | 第24章 解直角三角形易错疑难集训习题课件(20张PPT)2023-2024学年华东师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 810.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览

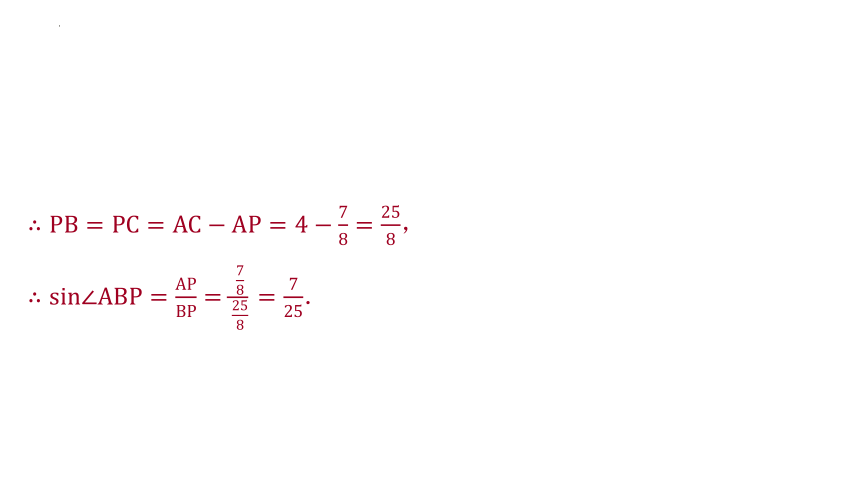






文档简介
(共20张PPT)
快速核答案
过易错 教材易混易错集训
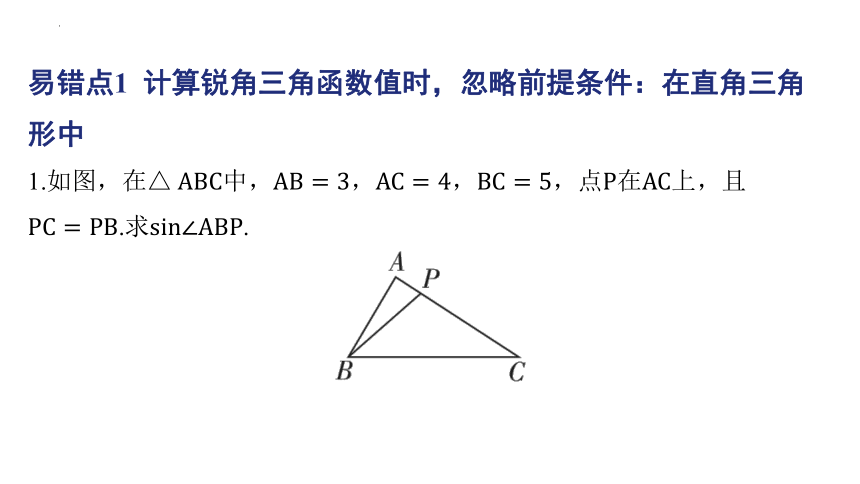
易错点1 计算锐角三角函数值时,忽略前提条件:在直角三角形中
1.解:
设
在
易错点2 忽略锐角三角函数的取值范围
2.解:
在
过疑难 常考疑难问题突破
疑难点 三角形与四边形的综合应用
1.解:在
由平移的性质可知,
2.(1)解:
(2)设
整理得,
舍去),
易错疑难集训
过易错 教材易混易错集训
易错点1 计算锐角三角函数值时,忽略前提条件:在直角三角
形中
1.如图,在中,,,,点在 上,且
.求 .
解:,,, ,
是直角三角形,且 .
设,则 .
在中, ,
,解得, ,
,
.
易错点2 忽略锐角三角函数的取值范围
2.在中, ,.若是方程 的根,求
的长.
解: 方程的根为 或1,
或 .
在中, , 为锐角,
, .
, .
【易错分析】
本题中没有说明 ,直接应用正弦函数的定义进行解答是错
误的,应先证明为直角三角形且 后才能应用正弦函数的
定义进行解答.
易错疑难集训
过疑难 常考疑难问题突破
疑难点 三角形与四边形的综合应用
1.[2023赤峰中考改编]如图,在 中,
,,,是 的中点,
连接,把线段沿射线方向平移到,点 在
上,求线段 在平移过程中扫过区域形成的四边
形 的周长和面积.
解:在中, ,,, .
是的中点, ,
由平移的性质可知,, ,
四边形是平行四边形,, ,
.
是的中点,是 的中点,
是的中位线, ,
四边形的周长为 ,面积为
.
2.新情境[2023湖州中考改编]如图,标号为①,②,
③,④的四个直角三角形和标号为⑤的正方形恰
好拼成对角互补的四边形 ,相邻图形之间
互不重叠也无缝隙,①和②分别是等腰直角三角
形和,③和④分别是 和
,⑤是正方形,直角顶点, ,
,分别在边,,, 上.
(1)若,,求 的长;
解:和 都是等腰直角三角形,
, .
, ,
.
, .
(2)若,求 的值.
设,已知,设, .
四边形是正方形, .
和 都是等腰直角三角形,
,, ,
,
.
四边形 的对角互补,
, .
四边形是正方形, ,
, ,
,, ,
整理得,,解得, (不合题意,
舍去),
.
快速核答案
过易错 教材易混易错集训
易错点1 计算锐角三角函数值时,忽略前提条件:在直角三角形中
1.解:
设
在
易错点2 忽略锐角三角函数的取值范围
2.解:
在
过疑难 常考疑难问题突破
疑难点 三角形与四边形的综合应用
1.解:在
由平移的性质可知,
2.(1)解:
(2)设
整理得,
舍去),
易错疑难集训
过易错 教材易混易错集训
易错点1 计算锐角三角函数值时,忽略前提条件:在直角三角
形中
1.如图,在中,,,,点在 上,且
.求 .
解:,,, ,
是直角三角形,且 .
设,则 .
在中, ,
,解得, ,
,
.
易错点2 忽略锐角三角函数的取值范围
2.在中, ,.若是方程 的根,求
的长.
解: 方程的根为 或1,
或 .
在中, , 为锐角,
, .
, .
【易错分析】
本题中没有说明 ,直接应用正弦函数的定义进行解答是错
误的,应先证明为直角三角形且 后才能应用正弦函数的
定义进行解答.
易错疑难集训
过疑难 常考疑难问题突破
疑难点 三角形与四边形的综合应用
1.[2023赤峰中考改编]如图,在 中,
,,,是 的中点,
连接,把线段沿射线方向平移到,点 在
上,求线段 在平移过程中扫过区域形成的四边
形 的周长和面积.
解:在中, ,,, .
是的中点, ,
由平移的性质可知,, ,
四边形是平行四边形,, ,
.
是的中点,是 的中点,
是的中位线, ,
四边形的周长为 ,面积为
.
2.新情境[2023湖州中考改编]如图,标号为①,②,
③,④的四个直角三角形和标号为⑤的正方形恰
好拼成对角互补的四边形 ,相邻图形之间
互不重叠也无缝隙,①和②分别是等腰直角三角
形和,③和④分别是 和
,⑤是正方形,直角顶点, ,
,分别在边,,, 上.
(1)若,,求 的长;
解:和 都是等腰直角三角形,
, .
, ,
.
, .
(2)若,求 的值.
设,已知,设, .
四边形是正方形, .
和 都是等腰直角三角形,
,, ,
,
.
四边形 的对角互补,
, .
四边形是正方形, ,
, ,
,, ,
整理得,,解得, (不合题意,
舍去),
.
