24.4 解直角三角形(第1课时)习题课件(22张PPT)2023-2024学年华东师大版数学九年级上册
文档属性
| 名称 | 24.4 解直角三角形(第1课时)习题课件(22张PPT)2023-2024学年华东师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览




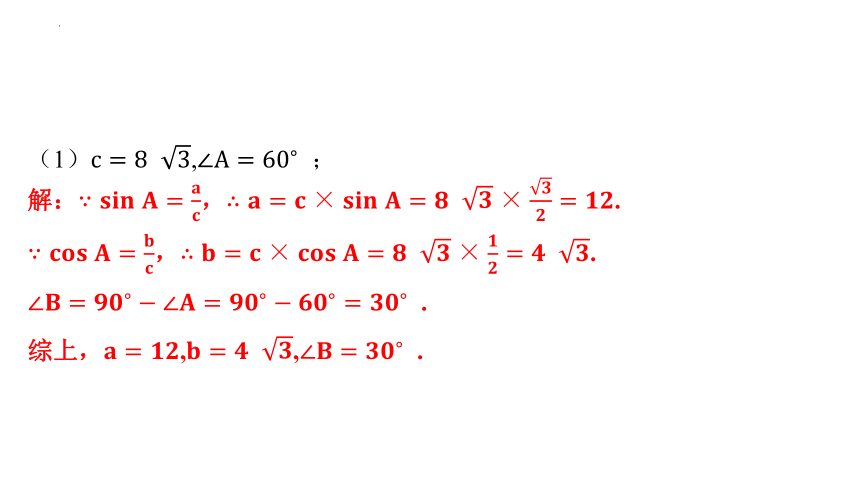
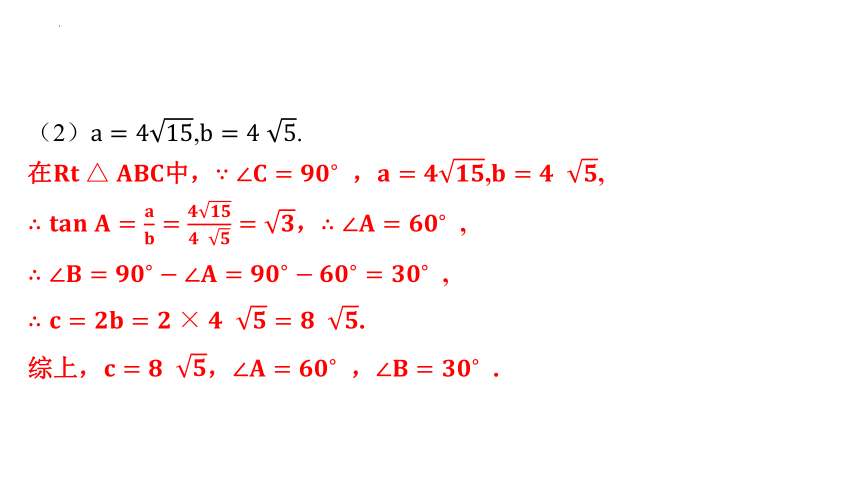


文档简介
(共22张PPT)
24.4 解直角三角形
课时1 解直角三角形(1)
过基础 教材必备知识精练
知识点1 解直角三角形
1.[2023蚌埠蚌山区段考]在中,, ,
,则 的度数为( )
C
A. B. C. D.
【解析】 在中,,, ,
, .
2.[2023上海徐汇区位育中学期中]在中, ,若
,,则 的长是_____.
3.在中, ,,,所对的边分别为,, ,根据下列条
件求这个三角形的其他未知元素:
【归纳总结】
(1)每个三角形都有6个元素,即3条边和3个角;(2)正弦、余弦、
正切三种函数都涉及两边一角,利用三角函数的定义列式求值时,不能将
它们的边和角弄混;(3)每个直角三角形均有一个直角,且两锐角互余,
三边满足勾股定理.
(1), ;
解:, .
, .
.
综上,,, .
(2), .
在中, ,, ,
, ,
,
.
综上,, , .
知识点2 解直角三角形的应用——方位角问题
4.[2024西安莲湖区期末]如图,小明和小华同时从 处分别向北
偏东 和南偏东 方向出发,他们的速度分别是 和
,则 后他们之间的距离为( )
D
A. B. C. D.
【解析】 ,
, ,
.
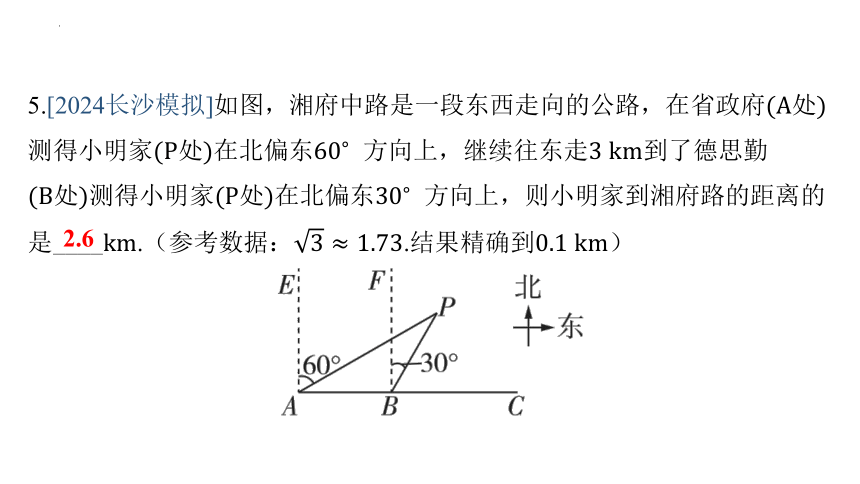
5.[2024长沙模拟]如图,湘府中路是一段东西走向的公路,在省政府处
测得小明家处在北偏东 方向上,继续往东走到了德思勤
处测得小明家处在北偏东 方向上,则小明家到湘府路的距离的是____.(参考数据:.结果精确到 )
2.6
【解析】 如图,过点作交的延长线于点 ,由题意得,
, ,
, ,
.在中, , ,
, 小明家到湘府路的距离约为
.
6.教材P113练习 变式[2023丹东中考]一艘
轮船由西向东航行,行驶到 岛时,测得灯
塔在岛的北偏东 方向上,继续向东航
行到达港,此时测得灯塔在 岛
的北偏西 方向上,求轮船在航行过程中与灯塔 的最短距离.
(结果精确到,参考数据:,,
,,, )
解:如图,过点作于点 ,
则 , ,
,
, .
,
,
.
答:轮船在航行过程中与灯塔 的最短距离为
.
24.4 解直角三角形
课时1 解直角三角形(1)
过能力 学科关键能力构建
第1题图
1.[2023西安期中]如图,在 中,
,,点为 边上一点,且
.若 ,则
( )
C
A.3 B.4 C.5 D.6
【解析】 在中,, ,
, ,
.
第2题图
2.[2022锦州中考]如图,一艘货轮在海面上航行,准
备要停靠到码头,货轮航行到处时,测得码头
在北偏东 方向上.为了躲避, 之间的暗礁,
这艘货轮调整航向,沿着北偏东 方向继续航行,
当它航行到处后,又沿着南偏东 方向航行20海
里到达码头,则货轮从到 航行的距离是______
海里.(结果精确到0.1海里,参考数据:
,, )
【解析】
3.[2022齐齐哈尔中考]在中,,, ,求
的值.
解:分情况讨论:
①如图1,当为锐角三角形时,过点作于点 ,
, , ,
, .
②如图2,当 为钝角三角
形时,
过点作,交 的延长
线于点 ,
, ,
,
,
.
综上,的长为 或
.
素养提升
4.应用意识[2022重庆中考A卷]如图,三角形
花园紧邻湖泊,四边形 是沿湖泊
修建的人行步道.经测量,点在点 的正东
方向,米,点在点 的正北方向,
点,在点的正北方向,米.点
在点的北偏东 方向上,点在点 的北
偏东 方向上.
(1)求步道 的长度;(结果精确到1米)
解:如图,过点作 的延长线
于点 ,
则四边形 是矩形,
米,
在中, ,
,
(米).
(2)点处有直饮水,小红从出发沿人行步道去取水,可以经过点 到
达点,也可以经过点到达点 .请计算说明她走哪一条路较近.
(参考数据:, )
点在点的北偏东 方向上,即 ,且 ,
,
在中,米, 米,
经过点到达点的路程为 (米),
(米).
在(1)的基础上知, ,
(米),
经过点到达点的路程为 (米),
, 小红经过点到达点 较近.
24.4 解直角三角形
课时1 解直角三角形(1)
过基础 教材必备知识精练
知识点1 解直角三角形
1.[2023蚌埠蚌山区段考]在中,, ,
,则 的度数为( )
C
A. B. C. D.
【解析】 在中,,, ,
, .
2.[2023上海徐汇区位育中学期中]在中, ,若
,,则 的长是_____.
3.在中, ,,,所对的边分别为,, ,根据下列条
件求这个三角形的其他未知元素:
【归纳总结】
(1)每个三角形都有6个元素,即3条边和3个角;(2)正弦、余弦、
正切三种函数都涉及两边一角,利用三角函数的定义列式求值时,不能将
它们的边和角弄混;(3)每个直角三角形均有一个直角,且两锐角互余,
三边满足勾股定理.
(1), ;
解:, .
, .
.
综上,,, .
(2), .
在中, ,, ,
, ,
,
.
综上,, , .
知识点2 解直角三角形的应用——方位角问题
4.[2024西安莲湖区期末]如图,小明和小华同时从 处分别向北
偏东 和南偏东 方向出发,他们的速度分别是 和
,则 后他们之间的距离为( )
D
A. B. C. D.
【解析】 ,
, ,
.
5.[2024长沙模拟]如图,湘府中路是一段东西走向的公路,在省政府处
测得小明家处在北偏东 方向上,继续往东走到了德思勤
处测得小明家处在北偏东 方向上,则小明家到湘府路的距离的是____.(参考数据:.结果精确到 )
2.6
【解析】 如图,过点作交的延长线于点 ,由题意得,
, ,
, ,
.在中, , ,
, 小明家到湘府路的距离约为
.
6.教材P113练习 变式[2023丹东中考]一艘
轮船由西向东航行,行驶到 岛时,测得灯
塔在岛的北偏东 方向上,继续向东航
行到达港,此时测得灯塔在 岛
的北偏西 方向上,求轮船在航行过程中与灯塔 的最短距离.
(结果精确到,参考数据:,,
,,, )
解:如图,过点作于点 ,
则 , ,
,
, .
,
,
.
答:轮船在航行过程中与灯塔 的最短距离为
.
24.4 解直角三角形
课时1 解直角三角形(1)
过能力 学科关键能力构建
第1题图
1.[2023西安期中]如图,在 中,
,,点为 边上一点,且
.若 ,则
( )
C
A.3 B.4 C.5 D.6
【解析】 在中,, ,
, ,
.
第2题图
2.[2022锦州中考]如图,一艘货轮在海面上航行,准
备要停靠到码头,货轮航行到处时,测得码头
在北偏东 方向上.为了躲避, 之间的暗礁,
这艘货轮调整航向,沿着北偏东 方向继续航行,
当它航行到处后,又沿着南偏东 方向航行20海
里到达码头,则货轮从到 航行的距离是______
海里.(结果精确到0.1海里,参考数据:
,, )
【解析】
3.[2022齐齐哈尔中考]在中,,, ,求
的值.
解:分情况讨论:
①如图1,当为锐角三角形时,过点作于点 ,
, , ,
, .
②如图2,当 为钝角三角
形时,
过点作,交 的延长
线于点 ,
, ,
,
,
.
综上,的长为 或
.
素养提升
4.应用意识[2022重庆中考A卷]如图,三角形
花园紧邻湖泊,四边形 是沿湖泊
修建的人行步道.经测量,点在点 的正东
方向,米,点在点 的正北方向,
点,在点的正北方向,米.点
在点的北偏东 方向上,点在点 的北
偏东 方向上.
(1)求步道 的长度;(结果精确到1米)
解:如图,过点作 的延长线
于点 ,
则四边形 是矩形,
米,
在中, ,
,
(米).
(2)点处有直饮水,小红从出发沿人行步道去取水,可以经过点 到
达点,也可以经过点到达点 .请计算说明她走哪一条路较近.
(参考数据:, )
点在点的北偏东 方向上,即 ,且 ,
,
在中,米, 米,
经过点到达点的路程为 (米),
(米).
在(1)的基础上知, ,
(米),
经过点到达点的路程为 (米),
, 小红经过点到达点 较近.
