对数函数及其性质 课件

课件42张PPT。12:38:1011、对数的概念：2、指数函数的定义:如果a b = N ，那么数b叫做以a为底N的对数，记作log a N＝b（a>0,a≠1）y=ax ( a ＞ 0, 且 a ≠ 1 ) 叫做指数函数,其中
x是自变量.函数的定义域是 R，值域是(0,+∞)12:38:102 如果把这个函数表示成对数的形式应为（ ）x=log2y 如果用x表示自变量，y表示函数，那么这个函数应为( ）y = log 2 x回忆学习指数函数时有这么一道练习： y = 2 x12:38:1032.2.2 对数函数及其性质 一般地,函数y = loga x(a＞0,且a≠ 1)叫做对数函数.其中 x是自变量.函数的定义域是（0,+∞）.对数函数的定义：注意:对数函数对底数的限制条件：a＞0,且a≠ 112:38:105根据对数函数的定义，请判断下列函数中那些是对数函数？ 反思小结：一个函数为对数的条件是：
系数为1；
底数为大于0且不等于1的常数；
真数为单个自变量。 (a>0,且a≠1)；
(a>0,且a≠1)；
12:38:106 一般地，函数y = loga x (a＞0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是（ 0 , +∞）求下列函数的定义域：我试试我理解12:38:107解:∵x2 ﹥0 即x ≠ 0

∴函数y= logax2 的定义域是{x| x ≠ 0}
（2）
解:∵ 4-x ﹥0即x ﹤4
∴函数y= loga (4-x) 的定义域是{x|x ﹤4 }
例7 求下列函数的定义域：
（1）12:38:108练习：课本73页2（1）（2）12:38:109问题：知道了对数函数的定义，如何研究对数函数的性质呢？你能类比前面讨论指数函数性质的思路，提出研究对数函数性质的方法和内容吗？
研究方法：
研究内容：画出函数的图象，结合图象研究函数的性质．
定义域、值域、特征点、单调性、奇偶性12:38:1010在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③连线。对数函数:y = loga x (a＞0,且a≠ 1） 图象与性质
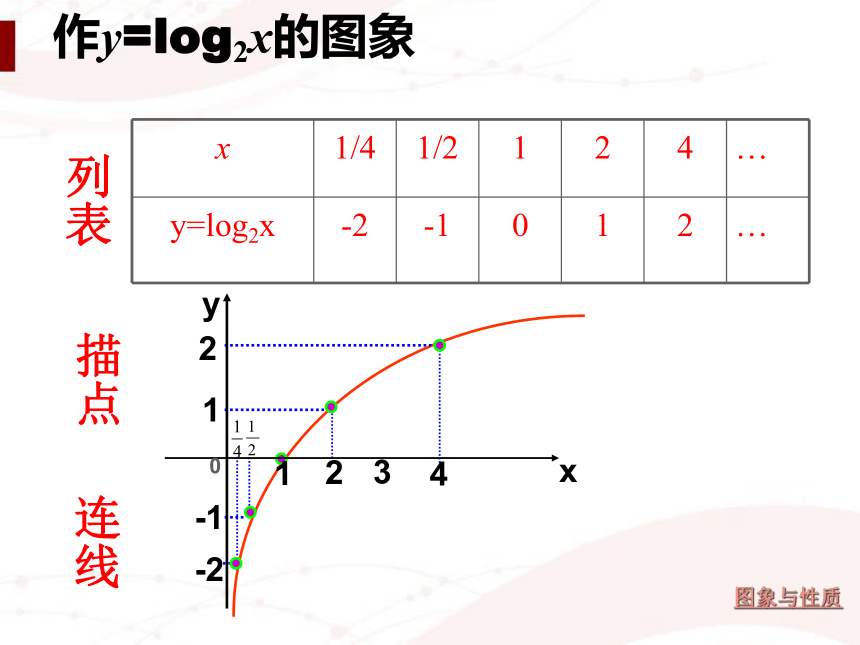
列表描点作y=log2x的图象连线 图象与性质
定义域 :( 0,+∞) 值 域 :R
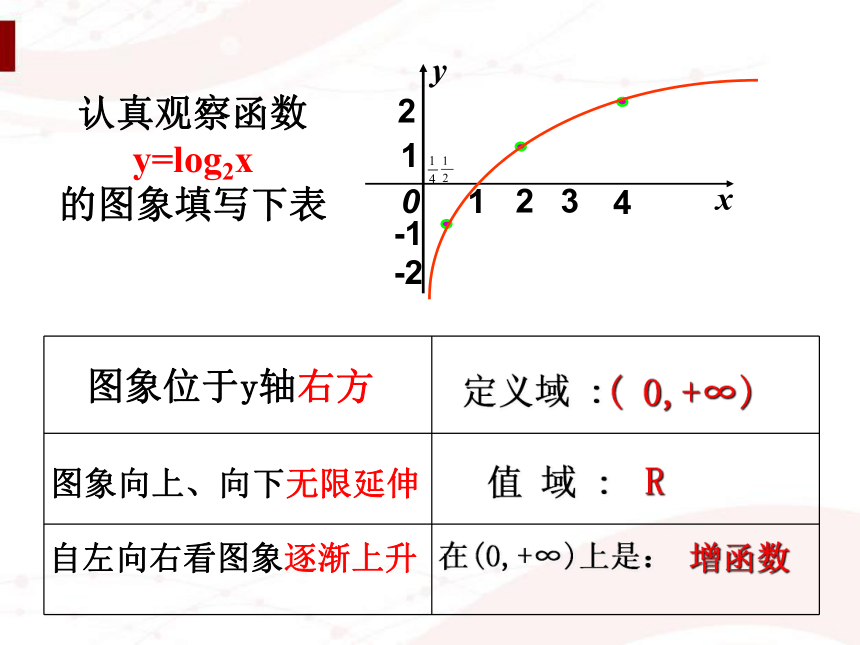
增函数在(0,+∞)上是：认真观察函数y=log2x
的图象填写下表图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐上升21-1-21240x3y列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 这两个函数的图象有什么关系呢？关于x轴对称… … … … … … 认真观察函数
的图象填写下表定义域 :( 0,+∞) 值 域 :R
减函数在(0,+∞)上是：图象位于y轴右方图象向上、向下无限延伸自左向右看图象逐渐下降12:38:1015对数函数y=log a x (a>0, a≠1)(4) 当0 当x>1时, y>0(4) 当00;
当x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域： (0,+∞)(2) 值域：Rxyo(1, 0)xyo（1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质12:38:1016(-1,3)全优61页基础夯实-1全优98页限时规范训练（一）12:38:1017C全优61页能力提高12:38:1018解：(1)由题意，得lg(2－x)≥0，即2－x≥1，所以 x≤1，全优60页变式训练12:38:1019全优61页能力提高12:38:1020问题：
猜想下列对数函数分别对应图中哪个函数图象？ 猜想与思考：对应 ；
对应 ；
对应 ；
12:38:1021下列是6个对数函数的图象，看看他们有什么规律.我试试我理解12:38:1022 底数a>1时,底数越大,其图象越接近x轴。补充性质二（只看第一象限） 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1　　底数0（1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1：画图找点比高低解法2：利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间（0，+∞）
上是增函数；∵3.4<8.5∴ log23.4< log28.512:38:1026（1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7解法2：考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间（0，+∞）上是减函数；
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 (2)解法1：画图找点比高低小结12:38:1027（1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:１.观察底数是大于1还是小于1（ a>1时为增函数
　　　　　　　　　　　　　　0 1 （3） loga5.1与 loga5.9解: ①若a>1则函数在区间（0，+∞）上是增函数；
∵5.1<5.9 ∴ loga5.1 < loga5.9②若0 ∵5.1<5.9 ∴ loga5.1 > loga5.912:38:1029全优64页能力提高12:38:1030你能口答吗？变一变还能口答吗？＜＞＞＜＜＜＜＜练习：课本73页312:38:1031解：∵log34>1,0 又f(x)＝log2x在(0，＋∞)上是增函数，
∴log2(x2－4x＋6)≥log22＝1.
∴函数的值域是[1，＋∞)．(3)∵x2－4x－5＝(x－2)2－9≥－9，
∴x2－4x－5能取得所有正实数．
∴函数y＝log2(x2－4x－5)的值域是R.全优63页典例剖析12:38:1036先看y=2x 与y=log2x指数函数、对数函数的图像有何关系呢？指数函数与对数函数图象间的关系指数函数与对数函数图像间的关系12:38:1039思考1:设某物体以3m/s的速度作匀速直线运动，分别以位移s和时间t为自变量，可以得到哪两个函数？这两个函数相同吗？ 思考2:设 ，分别x、y为自变量可以得到哪两个函数？这两个函数相同吗？ 得到和s=3t12:38:1040思考3:我们把具有上述特征的两个函数互称为反函数，那么函数y＝ax（a＞0，且a≠1）的反函数是什么？函数 的反函数是什么？ 小结:求反函数的一般步骤分三步
一解、二换、三注明．一般的，原函数的定义域就是反函数的值域,原函数的值域是反函数的定义域,
它们的图象关于直线y=x对称,原函数与反函数具有相同的单调性.12:38:1042全优98页限时规范训练（二）