第1课时 比例的意义 课件人教版六年级数学下册(共21张PPT)
文档属性
| 名称 | 第1课时 比例的意义 课件人教版六年级数学下册(共21张PPT) | 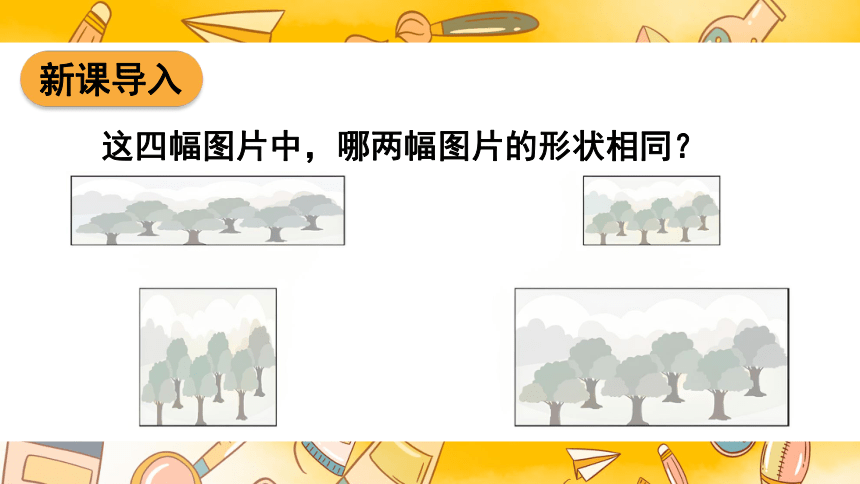 | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 13:35:03 | ||
图片预览






文档简介
(共21张PPT)
新课导入
这四幅图片中,哪两幅图片的形状相同?
六年级下册
比例的意义
1.比例的意义和基本性质
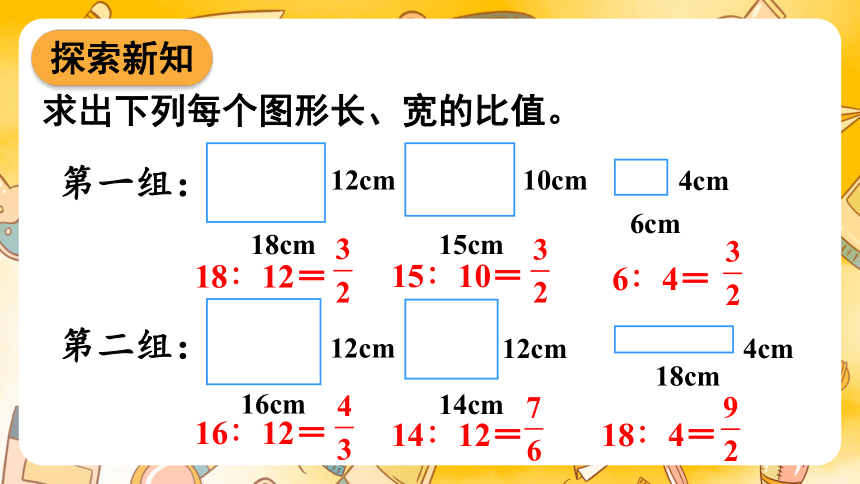
求出下列每个图形长、宽的比值。
第一组:
18cm
12cm
15cm
10cm
6cm
4cm
18∶12=
15∶10=
6∶4=
16cm
12cm
14cm
12cm
18cm
4cm
16∶12=
14∶12=
18∶4=
第二组:
探索新知
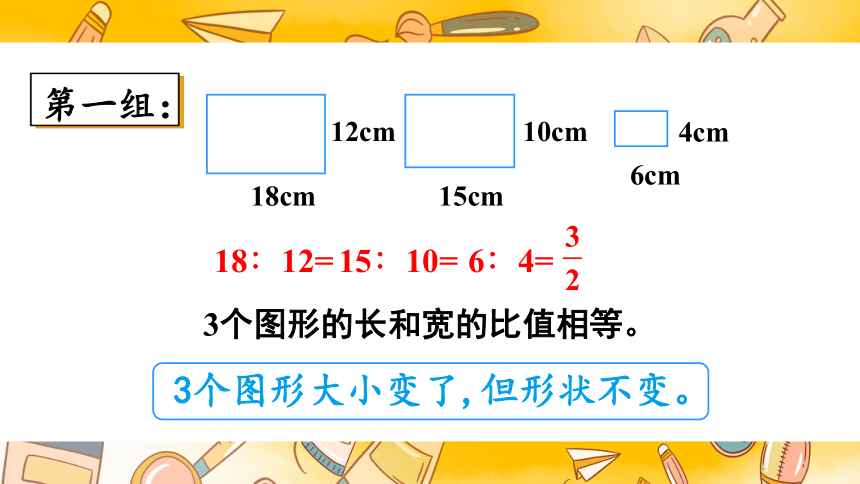
3个图形的长和宽的比值相等。
3个图形大小变了,但形状不变。
第一组:
18cm
12cm
15cm
10cm
6cm
4cm
18∶12=
15∶10=
6∶4=
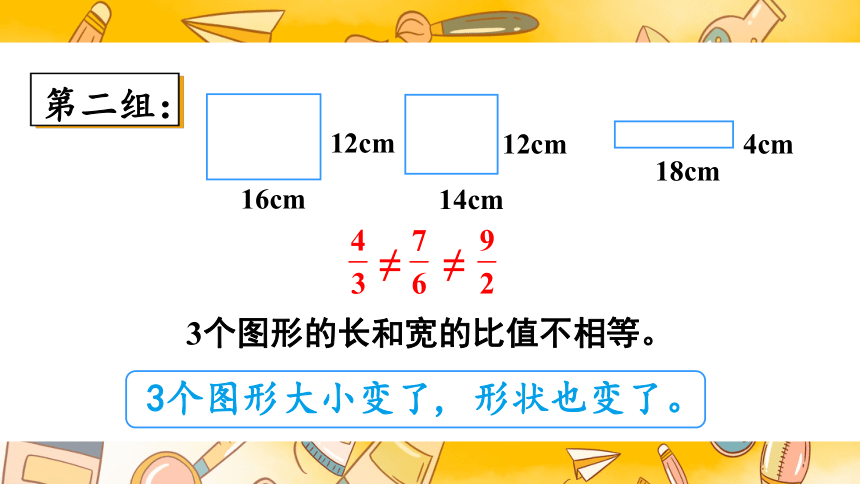
≠
≠
3个图形的长和宽的比值不相等。
3个图形大小变了, 形状也变了。
第二组:
16cm
12cm
14cm
12cm
18cm
4cm
18∶12=15∶10 18∶12=6∶4
15∶10=6∶4
比值相等的两个比,可以用等式来表示:
像这样表示两个比相等的式子叫作比例。
归纳总结
1.符合什么条件的比才是比例?
2.比例与比有什么区别和联系?
自学提示:
1.比例要符合“两个比”和“一个等式”。
2.必须是两个比值相等的比组成的等式。
3.比例与比的区别和联系是:比是由两个数组成的,而比例是由两个比值相等的比组成的。
归纳
4.两数相除叫作两个数的比,而表示两个比相等的式子叫作比例。
5.比由两个数组成,而比例由四个数组成。
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
请你们看看这三面国旗的尺寸,它们的长与宽的比是不是也能组成比例呢?
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
5∶ =2.4∶1.6
5∶ =60∶40
2.4∶1.6=60∶40
这三面国旗的尺寸中,还有哪些比可以组成比例?
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
这些国旗宽与长的比可以组成比例,例如1.6∶2.4=40∶60。
这些国旗长的比和宽的比也可以组成比例,例如5∶2.4= ∶1.6。
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
国旗尺寸中任意两个数据组成的比都能组成比例吗?
天安门国旗的长∶天安门国旗的宽和学校国旗的宽∶学校国旗的长可以组成比例吗?
易错点:两个比的比值要相等才能组成比例。
下面哪组中的两个比可以组成比例?把组成的比例写出来。
(1)6∶10和9∶15
6∶10=0.6 9∶15=0.6
因为0.6=0.6,所以6∶10=9∶15
【教材P38 做一做 第1题】
(2)20∶5和1∶4
20∶5=4 1∶4=0.25
因为4≠0.25,所以不能组成比例
(3) ∶ 和6∶4
∶ =1.5 6∶4=1.5
因为1.5=1.5,所以
∶ =6∶4
(4)0.6∶0.2和 ∶
0.6∶0.2=3 ∶ =3
因为3=3,所以0.6∶0.2= ∶
1.下面各表中相对应的两个量的比能否组成比例?如果能,把组成的比例写出来。
不能组成比例
能组成比例,
30∶2=120∶8
年龄/岁 12 14
身高/m 1.4 1.6
箱子数量/个 2 8
质量/kg 30 120
不能组成比例
能组成比例,
400∶5=800∶10
时间/时 2 3
路程/km 30 40
衣服数量/件 5 10
总价/元 400 800
随堂练习
【教材P41 练习八 第1题】
2.下面哪组中的四个数可以组成比例?把组成的比例写出来。
(1)4,5,12和15
(2)2,3,4和5
不能组成比例
4∶5=12∶15
【教材P41 练习八 第2题】
(3)1.6,6.4,2和5
不能组成比例
3.写出比值是5的两个比,并组成比例。
10∶2=20∶4
10∶2
20∶4
(答案不唯一)
【教材P41 练习八 第3题】
4.用右图中的4个数据可以组成哪些比例?
3∶1.5=4∶2
1.5∶3=2∶4
3∶4=1.5∶2
4∶3=2∶1.5
2∶1.5=4∶3
1.5∶2=3∶4
2∶4=1.5∶3
4∶2=3∶1.5
【教材P38 做一做 第2题】
课堂小结
同学们,今天的数学课你们有哪些收获呢?
5∶ =2.4∶1.6
5∶ =60∶40
2.4∶1.6=60∶40
表示两个比相等的式子叫作比例。
判断两个比组成比例的方法:
看它们的比值是否相等,若比值相等则能组成比例,若比值不相等则不能组成比例。
新课导入
这四幅图片中,哪两幅图片的形状相同?
六年级下册
比例的意义
1.比例的意义和基本性质
求出下列每个图形长、宽的比值。
第一组:
18cm
12cm
15cm
10cm
6cm
4cm
18∶12=
15∶10=
6∶4=
16cm
12cm
14cm
12cm
18cm
4cm
16∶12=
14∶12=
18∶4=
第二组:
探索新知
3个图形的长和宽的比值相等。
3个图形大小变了,但形状不变。
第一组:
18cm
12cm
15cm
10cm
6cm
4cm
18∶12=
15∶10=
6∶4=
≠
≠
3个图形的长和宽的比值不相等。
3个图形大小变了, 形状也变了。
第二组:
16cm
12cm
14cm
12cm
18cm
4cm
18∶12=15∶10 18∶12=6∶4
15∶10=6∶4
比值相等的两个比,可以用等式来表示:
像这样表示两个比相等的式子叫作比例。
归纳总结
1.符合什么条件的比才是比例?
2.比例与比有什么区别和联系?
自学提示:
1.比例要符合“两个比”和“一个等式”。
2.必须是两个比值相等的比组成的等式。
3.比例与比的区别和联系是:比是由两个数组成的,而比例是由两个比值相等的比组成的。
归纳
4.两数相除叫作两个数的比,而表示两个比相等的式子叫作比例。
5.比由两个数组成,而比例由四个数组成。
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
请你们看看这三面国旗的尺寸,它们的长与宽的比是不是也能组成比例呢?
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
5∶ =2.4∶1.6
5∶ =60∶40
2.4∶1.6=60∶40
这三面国旗的尺寸中,还有哪些比可以组成比例?
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
这些国旗宽与长的比可以组成比例,例如1.6∶2.4=40∶60。
这些国旗长的比和宽的比也可以组成比例,例如5∶2.4= ∶1.6。
天安门广场的国旗:长5m,宽 m。
学校操场的国旗:长2.4m,宽1.6m。
教室里的国旗:长60cm,宽40cm。
国旗尺寸中任意两个数据组成的比都能组成比例吗?
天安门国旗的长∶天安门国旗的宽和学校国旗的宽∶学校国旗的长可以组成比例吗?
易错点:两个比的比值要相等才能组成比例。
下面哪组中的两个比可以组成比例?把组成的比例写出来。
(1)6∶10和9∶15
6∶10=0.6 9∶15=0.6
因为0.6=0.6,所以6∶10=9∶15
【教材P38 做一做 第1题】
(2)20∶5和1∶4
20∶5=4 1∶4=0.25
因为4≠0.25,所以不能组成比例
(3) ∶ 和6∶4
∶ =1.5 6∶4=1.5
因为1.5=1.5,所以
∶ =6∶4
(4)0.6∶0.2和 ∶
0.6∶0.2=3 ∶ =3
因为3=3,所以0.6∶0.2= ∶
1.下面各表中相对应的两个量的比能否组成比例?如果能,把组成的比例写出来。
不能组成比例
能组成比例,
30∶2=120∶8
年龄/岁 12 14
身高/m 1.4 1.6
箱子数量/个 2 8
质量/kg 30 120
不能组成比例
能组成比例,
400∶5=800∶10
时间/时 2 3
路程/km 30 40
衣服数量/件 5 10
总价/元 400 800
随堂练习
【教材P41 练习八 第1题】
2.下面哪组中的四个数可以组成比例?把组成的比例写出来。
(1)4,5,12和15
(2)2,3,4和5
不能组成比例
4∶5=12∶15
【教材P41 练习八 第2题】
(3)1.6,6.4,2和5
不能组成比例
3.写出比值是5的两个比,并组成比例。
10∶2=20∶4
10∶2
20∶4
(答案不唯一)
【教材P41 练习八 第3题】
4.用右图中的4个数据可以组成哪些比例?
3∶1.5=4∶2
1.5∶3=2∶4
3∶4=1.5∶2
4∶3=2∶1.5
2∶1.5=4∶3
1.5∶2=3∶4
2∶4=1.5∶3
4∶2=3∶1.5
【教材P38 做一做 第2题】
课堂小结
同学们,今天的数学课你们有哪些收获呢?
5∶ =2.4∶1.6
5∶ =60∶40
2.4∶1.6=60∶40
表示两个比相等的式子叫作比例。
判断两个比组成比例的方法:
看它们的比值是否相等,若比值相等则能组成比例,若比值不相等则不能组成比例。
