第6单元正比例和反比例检测卷(含答案)2023-2024学年数学六年级下册苏教版
文档属性
| 名称 | 第6单元正比例和反比例检测卷(含答案)2023-2024学年数学六年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 393.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 13:47:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例检测卷2023-2024学年数学六年级下册苏教版
一、选择题
1.两个非零自然数X、Y,2.5X-3Y=0,那么X和Y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.下面几组相关联的量中,成正比例关系的是( )。
A.看一本书,平均每天看的页数和看的天数 B.圆锥的体积一定,它的底面积和高
C.修一条路,已经修的米数和未修的米数 D.商一定,被除数和除数
3.甲、乙两名运动员在百米短跑比赛中,速度比是11∶12,则甲、乙两名运动员所用的时间比是( )。
A.11∶12 B.11∶23 C.12∶11 D.23∶11
4.表示x和y成正比例关系的式子是( )。
A.x+y=12 B.y=0.8x C.x-y=20 D.xy=10
5.小明把不同数量的水倒入同样的杯子里,分别测得杯中水的高度和体积(如下表)。杯中水的体积和水的高度( )。
水的高度/cm 2 4 6 8 …
水的体积/cm3 50 100 150 200 …
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.如果甲、乙是两个成反比例的量,那么当甲增加50%时,乙一定会( )
A.增加50% B.减少 C.减少 D.减少50%
二、填空题
7.已知(a、b都是不为0的自然数),那么a和b成( )比例关系,a和b的最大公因数是( )。
8.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,( )和( )成( )比例关系。
9.有一个螺旋形弹簧,在200克以内,重物的重量与弹簧伸长的长度成正比例。在这个弹簧上,挂60克的重物,弹簧的长度为7厘米,当挂上120克的物时弹簧长度就为9厘米,什么也不挂时,弹簧本身的长度是( )厘米,挂上150克重物时,弹簧长度是( )厘米。
10.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
11.根据下表中的施药量,如果在16公顷的棉花地喷洒这种除草剂,需除草剂( )毫升;若有720毫升的除草剂,可以喷洒( )公顷的玉米地。
施药方法 用清水将本剂稀释后,均匀喷洒于杂草叶面上。 农作物 施药量(毫升∶公顷)
棉花 40∶1
水稻 55∶1
玉米 60∶1
12.小青身高1.2米,妈妈身高1.6米,她们在桃花坞站立合影,照片中量得小青身高6厘米。这张照片是把人按( ) 的比缩小了,照片中妈妈和小青的身高比是( )。
三、判断题
13.总路程一定,已行的路程和剩下的路程成反比例。( )
14.xy+2=k(一定),x和y不成比例。( )
15.圆的半径和周长成正比例。( )
16.圆的半径扩大,面积也扩大,半径缩小,面积缩小,所以圆面积和半径成正比例。( )
17.若,则a与b成反比例。( )
四、解答题
18.江苏省淮盐产场是中国四大盐场之一。其中,一个晒盐场用100克海水可以晒出6克盐。如果一块盐田一次放入650吨海水,可以晒出多少吨盐?
19.黄豆有很高的营养价值。据测定,50克黄豆的蛋白质含量相当于150克鸡蛋或600克牛奶的蛋白质含量。多少千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量?(列比例解答)
20.一间房子要用方砖铺地,用面积是36平方分米的方砖,需用96块,如果改用边长为8分米的方砖,需用多少块?(用比例解)
21.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如下表。如果用面积是36平方厘米的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例知识解答)
每个小正方形的面积 /平方厘米 4 9 16
所需小正方形的数量/个 216 96 54
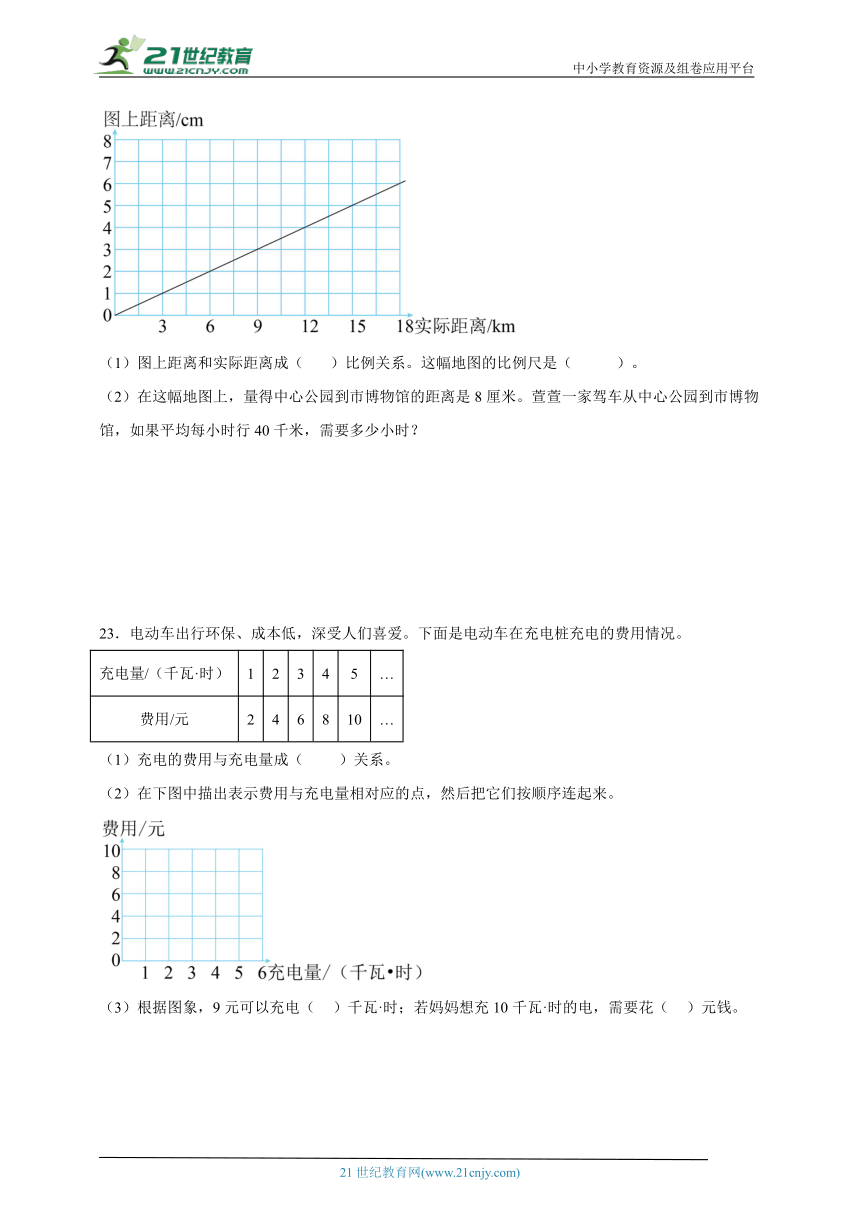
22.下面的图像表示某地地图上的图上距离和实际距离的关系。
(1)图上距离和实际距离成( )比例关系。这幅地图的比例尺是( )。
(2)在这幅地图上,量得中心公园到市博物馆的距离是8厘米。萱萱一家驾车从中心公园到市博物馆,如果平均每小时行40千米,需要多少小时?
23.电动车出行环保、成本低,深受人们喜爱。下面是电动车在充电桩充电的费用情况。
充电量/(千瓦·时) 1 2 3 4 5 …
费用/元 2 4 6 8 10 …
(1)充电的费用与充电量成( )关系。
(2)在下图中描出表示费用与充电量相对应的点,然后把它们按顺序连起来。
(3)根据图象,9元可以充电( )千瓦·时;若妈妈想充10千瓦·时的电,需要花( )元钱。
参考答案:
1.A
【分析】两个相关联的量,对应的比值一定,则成正比例;对应的乘积一定,则成反比例,除此以外,不成比例。因为2.5X-3Y=0,所以2.5X=3Y。再根据比例的基本性质,内项的乘积等于外项的乘积,可得出X和Y的比值,据此解答。
【详解】由2.5X-3Y=0,可得2.5X=3Y,
则X∶Y=3∶2.5=6∶5
所以X和Y的比值为,比值一定,成正比例。
故答案为:A
2.D
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】A.平均每天看的页数×看的天数=这本书的页数,看一本书,平均每天看的页数和看的天数成反比例关系;
B.圆锥底面积×高=体积×3,圆锥的体积一定,它的底面积和高成反比例关系;
C.已修的米数+未修的米数=总长度,修一条路,已经修的米数和未修的米数不成比例关系;
D.被除数÷除数=商,商一定,被除数和除数成正比例关系。
成正比例关系的是商一定,被除数和除数。
故答案为:D
3.C
【分析】根据“速度×时间=路程”可知,路程一定时,速度与时间成反比例关系,所以甲、乙两名运动员所用的时间比等于他们速度的反比。
【详解】甲、乙两名运动员在百米短跑比赛中,速度比是11∶12,则甲、乙两名运动员所用的时间比是12∶11。
故答案为:C
4.B
【分析】判断x与y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例。据此分析4个选项,找出正确的答案。
【详解】A.x+y=12,x与y的和一定,不符合正比例的意义;
B.y=0.8x,可得,y与x的比值一定,符合正比例的意义,所以x和y成正比例关系;
C.x-y=20,x与y的差一定,不符合正比例的意义;
D.xy=10,x与y的乘积一定,符合反比例的意义,所以x与y成反比例。
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
5.A
【分析】判断水的体积和水的高度之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;比值、乘积均不一定则不成比例;据此解答。
【详解】50∶2=50÷2=25
100∶4=100÷4=25
150∶6=150÷6=25
200∶8=200÷8=25
杯中水的体积和水的高度的比值一定,所以杯中水的体积和水的高度成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
6.B
【分析】如果甲、乙是两个成反比例的量,那么甲×乙的积是一定的,甲增加50%就是甲×(1+50%),将选项中的描述代入,运算之后依然是甲×乙即可。
【详解】A.增加50%,甲×(1+50%)×乙×(1+50%)=甲×乙×1.5×1.5=甲×乙×2.25,选项错误;
B.减少,甲×(1+50%)×乙×(1-)=甲×乙×1.5×=甲×乙,选项正确;
C.减少,甲×(1+50%)×乙×(1-)=甲×乙×1.5×=甲×乙×0.5,选项错误;
D.减少50%,甲×(1+50%)×乙×(1-50%)=甲×乙×1.5×0.5=甲×乙×0.75,选项错误。
故答案为:B
【点睛】本题考查了反比例的应用,两个相关联的量,积一定,是反比例。
7. 正 b
【分析】两个相关联的量,如果是比值一定,成正比例关系;如果是乘积一定,则成反比例关系。如果两个数是倍数关系,则它们的最大公因数是较小数,据此解答。
【详解】已知(a、b都是不为0的自然数),则 (a、b都是不为0的自然数),a和b的比值一定,那么a和b成正比例关系。a和b是倍数关系,所以a和b的最大公因数是b。
【点睛】此题考查了正反比例的辨别,以及最大公因数的求法。
8. 每行站的人数 站的行数 反
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例;据此解答。
【详解】由题意可知:每行站的人数×站的行数=六年级总人数(一定),即每行站的人数和站的行数的乘积一定,所以每行站的人数和站的行数成反比例关系。
【点睛】本题主要考查辨识成正比例的量和成反比例的量。
9. 5 10
【分析】根据题目可知,重物的重量与弹簧伸长的长度成正比例,同时挂60克的重物,弹簧的长度为7厘米,当挂上120克重物的时候,弹簧长度为9厘米,由此即可知道当弹簧多挂120-60=60克的重物的时候,弹簧伸长了9-7=2厘米,即60克伸长2厘米,则伸长1厘米对应的是60÷2=30克,由于挂60克伸长2厘米后是7厘米,原来是7-2=5厘米;当挂上150厘米,弹簧伸长:150÷30=5厘米,则弹簧长度:5+5=10厘米。
【详解】根据题意,弹簧每伸长1厘米,需要挂的重物的重量是:
(120-60)÷(9-7)
=60÷2
=30(克)
重物的重量与弹簧伸长成正比例
30克对应1厘米,60克对应弹簧伸长的厘米数是:
1×(60÷30)
=1×2
=2(厘米)
7-2=5(厘米)
1×(150÷30)+5
=1×5+5
=5+5
=10(厘米)
【点睛】本题考查正比例的应用,根据正比例的意义,进行解答问题。
10. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
11. 640 12
【分析】根据题意可知:除草剂÷种植农作物的面积=施药量(一定),即:除草剂和种植农作物的面积的比值一定,成正比例关系,据此列比例解答。
【详解】解:设在16公顷的棉花地喷洒这种除草剂,需除草剂x毫升。
x∶16=40∶1
x=16×40
x=640
设若有720毫升的除草剂,可以喷洒y公顷的玉米地。
720∶y=60∶1
60y=720
y=12
【点睛】解答此题的关键是:先判断题中的两种相关联的量成什么比例,并找准对应量。
12. 1∶20 4∶3
【分析】用小青照片中的身高比实际的身高,即可求出照片是把人按什么比缩小的;照片是按相同的比例将妈妈和小青的身高缩小的,所以根据实际高度写出妈妈和小青的身高比即可。
【详解】6厘米∶1.2米
=6厘米∶120厘米
=1∶20;
这张照片是把人按1∶20的比缩小的;
照片中妈妈和小青的身高比是1.6∶1.2=4∶3。
【点睛】明确图形放大与缩小中比的意义是解答本题的关键,比的前项表示变化后图形的边长,比的后项表示变化前图形的边长。
13.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为已走的路程+剩下的路程=总路程(一定),是和一定,
所以已走的路程和剩下的路程不成反比例;
故答案为:×
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】由分析可得:xy+2=k(一定),即xy=k-2(一定),是乘积一定,则x和y成反比例,所以原题说法错误。
故答案为:×
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】圆的周长=2×π×半径
圆的周长÷它的半径=2π,是比值一定
所以圆的半径和周长成正比例,原题干说法正确
故答案为:√
【点睛】本题考查正比例和反比例的意义及辨识,根据正比例和反比例的意义进行解答。
16.×
【分析】判断圆的半径和面积是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果是比值不一定,就不成正比例。
【详解】圆的面积÷半径=圆周率×半径(不一定),是比值不一定,圆的半径和面积不成正比例。
故答案为:×
【点睛】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断。
17.√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;据此进行判断。
【详解】若ab-8=125,即ab=133,是乘积一定,则a与b成反比例;
原题说法正确。
故答案为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
18.39吨
【分析】根据题意知道,海水的质量和盐的质量的比值一定,所以海水的质量和盐的质量成正比例,由此列式解答即可。
【详解】解:设可以晒出x吨盐。
100∶6=650∶x
100x=6×650
100x=3900
100x÷100=3900÷100
x=39
答:可以晒出39吨盐。
19.1千克
【分析】设x多少千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量,已知50克黄豆的蛋白质含量相当于600克牛奶的蛋白质含量,列出正比例算式解答即可。
【详解】600克=0.6千克 50克=0.05千克
解:设x千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量。
0.05∶0.6=x∶12
0.6x=0.05×12
0.6x=0.6
0.6x÷0.6=0.6÷0.6
x=1
答:1千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量。
20.54块
【分析】根据题意,一块方砖的面积×方砖的块数=这间房子地面的面积(一定),所以一块方砖的面积与方砖的块数成反比例。由此设需用x块,列出比例式(8×8)×x=96×36即可解决问题。
【详解】解:设需要x块砖。
(8×8)×x=96×36
64x=3456
64x÷64=3456÷64
x=54
答:需要54块。
21.24个
【分析】
每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。设需要x个小正方形,长方形彩纸的面积=36×需要小正方形个数,由此解答即可。
【详解】
解:设需要x个小正方形。
36x=216×4
36x=864
36x÷x=864÷36
x=24
答:需要24个小正方形。
22.(1)正;1∶300000
(2)0.6小时
【分析】
(1)正比例图像是一条经过原点的直线,观察图像即可确定比例关系;根据图上距离∶实际距离=比例尺,写出图上距离与实际距离的比,化简即可。
(2)根据实际距离=图上距离÷比例尺,求出中心公园到市博物馆的实际距离,再根据时间=路程÷速度,列式解答即可。
【详解】(1)1厘米∶3千米=1厘米∶300000厘米=1∶300000
图上距离和实际距离成正比例关系。这幅地图的比例尺是1∶300000。
(2)(厘米)
2400000厘米=24千米
24÷40=0.6(小时)
答:需要0.6小时。
23.(1)正比例
(2)见详解
(3)4.5;20
【分析】
(1)结合统计表中的数据,用=单价,发现单价一定,即比值一定,据此得出充电的费用与充电量成正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
(2)根据统计表中的数据,先在图中描出表示费用与充电量相对应的点,然后把它们按顺序连起来,完成正比例图象的绘制。
(3)由图象可知,电的单价是2元,求9元可以充电多少千瓦·时,根据“总价÷单价=数量”解答;求想充10千瓦·时的电,需要花多少元钱,根据“单价×数量=总价”解答。
【详解】(1)===…=2(一定)
比值一定,则充电的费用与充电量成正比例关系。
(2)如图:
(3)9÷2=4.5(千瓦·时)
2×10=20(元)
根据图象,9元可以充电4.5千瓦·时;若妈妈想充10千瓦·时的电,需要花20元钱。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例检测卷2023-2024学年数学六年级下册苏教版
一、选择题
1.两个非零自然数X、Y,2.5X-3Y=0,那么X和Y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.下面几组相关联的量中,成正比例关系的是( )。
A.看一本书,平均每天看的页数和看的天数 B.圆锥的体积一定,它的底面积和高
C.修一条路,已经修的米数和未修的米数 D.商一定,被除数和除数
3.甲、乙两名运动员在百米短跑比赛中,速度比是11∶12,则甲、乙两名运动员所用的时间比是( )。
A.11∶12 B.11∶23 C.12∶11 D.23∶11
4.表示x和y成正比例关系的式子是( )。
A.x+y=12 B.y=0.8x C.x-y=20 D.xy=10
5.小明把不同数量的水倒入同样的杯子里,分别测得杯中水的高度和体积(如下表)。杯中水的体积和水的高度( )。
水的高度/cm 2 4 6 8 …
水的体积/cm3 50 100 150 200 …
A.成正比例 B.成反比例 C.不成比例 D.无法判断
6.如果甲、乙是两个成反比例的量,那么当甲增加50%时,乙一定会( )
A.增加50% B.减少 C.减少 D.减少50%
二、填空题
7.已知(a、b都是不为0的自然数),那么a和b成( )比例关系,a和b的最大公因数是( )。
8.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?此题中,( )和( )成( )比例关系。
9.有一个螺旋形弹簧,在200克以内,重物的重量与弹簧伸长的长度成正比例。在这个弹簧上,挂60克的重物,弹簧的长度为7厘米,当挂上120克的物时弹簧长度就为9厘米,什么也不挂时,弹簧本身的长度是( )厘米,挂上150克重物时,弹簧长度是( )厘米。
10.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
11.根据下表中的施药量,如果在16公顷的棉花地喷洒这种除草剂,需除草剂( )毫升;若有720毫升的除草剂,可以喷洒( )公顷的玉米地。
施药方法 用清水将本剂稀释后,均匀喷洒于杂草叶面上。 农作物 施药量(毫升∶公顷)
棉花 40∶1
水稻 55∶1
玉米 60∶1
12.小青身高1.2米,妈妈身高1.6米,她们在桃花坞站立合影,照片中量得小青身高6厘米。这张照片是把人按( ) 的比缩小了,照片中妈妈和小青的身高比是( )。
三、判断题
13.总路程一定,已行的路程和剩下的路程成反比例。( )
14.xy+2=k(一定),x和y不成比例。( )
15.圆的半径和周长成正比例。( )
16.圆的半径扩大,面积也扩大,半径缩小,面积缩小,所以圆面积和半径成正比例。( )
17.若,则a与b成反比例。( )
四、解答题
18.江苏省淮盐产场是中国四大盐场之一。其中,一个晒盐场用100克海水可以晒出6克盐。如果一块盐田一次放入650吨海水,可以晒出多少吨盐?
19.黄豆有很高的营养价值。据测定,50克黄豆的蛋白质含量相当于150克鸡蛋或600克牛奶的蛋白质含量。多少千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量?(列比例解答)
20.一间房子要用方砖铺地,用面积是36平方分米的方砖,需用96块,如果改用边长为8分米的方砖,需用多少块?(用比例解)
21.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如下表。如果用面积是36平方厘米的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例知识解答)
每个小正方形的面积 /平方厘米 4 9 16
所需小正方形的数量/个 216 96 54
22.下面的图像表示某地地图上的图上距离和实际距离的关系。
(1)图上距离和实际距离成( )比例关系。这幅地图的比例尺是( )。
(2)在这幅地图上,量得中心公园到市博物馆的距离是8厘米。萱萱一家驾车从中心公园到市博物馆,如果平均每小时行40千米,需要多少小时?
23.电动车出行环保、成本低,深受人们喜爱。下面是电动车在充电桩充电的费用情况。
充电量/(千瓦·时) 1 2 3 4 5 …
费用/元 2 4 6 8 10 …
(1)充电的费用与充电量成( )关系。
(2)在下图中描出表示费用与充电量相对应的点,然后把它们按顺序连起来。
(3)根据图象,9元可以充电( )千瓦·时;若妈妈想充10千瓦·时的电,需要花( )元钱。
参考答案:
1.A
【分析】两个相关联的量,对应的比值一定,则成正比例;对应的乘积一定,则成反比例,除此以外,不成比例。因为2.5X-3Y=0,所以2.5X=3Y。再根据比例的基本性质,内项的乘积等于外项的乘积,可得出X和Y的比值,据此解答。
【详解】由2.5X-3Y=0,可得2.5X=3Y,
则X∶Y=3∶2.5=6∶5
所以X和Y的比值为,比值一定,成正比例。
故答案为:A
2.D
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【详解】A.平均每天看的页数×看的天数=这本书的页数,看一本书,平均每天看的页数和看的天数成反比例关系;
B.圆锥底面积×高=体积×3,圆锥的体积一定,它的底面积和高成反比例关系;
C.已修的米数+未修的米数=总长度,修一条路,已经修的米数和未修的米数不成比例关系;
D.被除数÷除数=商,商一定,被除数和除数成正比例关系。
成正比例关系的是商一定,被除数和除数。
故答案为:D
3.C
【分析】根据“速度×时间=路程”可知,路程一定时,速度与时间成反比例关系,所以甲、乙两名运动员所用的时间比等于他们速度的反比。
【详解】甲、乙两名运动员在百米短跑比赛中,速度比是11∶12,则甲、乙两名运动员所用的时间比是12∶11。
故答案为:C
4.B
【分析】判断x与y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例。据此分析4个选项,找出正确的答案。
【详解】A.x+y=12,x与y的和一定,不符合正比例的意义;
B.y=0.8x,可得,y与x的比值一定,符合正比例的意义,所以x和y成正比例关系;
C.x-y=20,x与y的差一定,不符合正比例的意义;
D.xy=10,x与y的乘积一定,符合反比例的意义,所以x与y成反比例。
故答案为:B
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断。
5.A
【分析】判断水的体积和水的高度之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;比值、乘积均不一定则不成比例;据此解答。
【详解】50∶2=50÷2=25
100∶4=100÷4=25
150∶6=150÷6=25
200∶8=200÷8=25
杯中水的体积和水的高度的比值一定,所以杯中水的体积和水的高度成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
6.B
【分析】如果甲、乙是两个成反比例的量,那么甲×乙的积是一定的,甲增加50%就是甲×(1+50%),将选项中的描述代入,运算之后依然是甲×乙即可。
【详解】A.增加50%,甲×(1+50%)×乙×(1+50%)=甲×乙×1.5×1.5=甲×乙×2.25,选项错误;
B.减少,甲×(1+50%)×乙×(1-)=甲×乙×1.5×=甲×乙,选项正确;
C.减少,甲×(1+50%)×乙×(1-)=甲×乙×1.5×=甲×乙×0.5,选项错误;
D.减少50%,甲×(1+50%)×乙×(1-50%)=甲×乙×1.5×0.5=甲×乙×0.75,选项错误。
故答案为:B
【点睛】本题考查了反比例的应用,两个相关联的量,积一定,是反比例。
7. 正 b
【分析】两个相关联的量,如果是比值一定,成正比例关系;如果是乘积一定,则成反比例关系。如果两个数是倍数关系,则它们的最大公因数是较小数,据此解答。
【详解】已知(a、b都是不为0的自然数),则 (a、b都是不为0的自然数),a和b的比值一定,那么a和b成正比例关系。a和b是倍数关系,所以a和b的最大公因数是b。
【点睛】此题考查了正反比例的辨别,以及最大公因数的求法。
8. 每行站的人数 站的行数 反
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例;据此解答。
【详解】由题意可知:每行站的人数×站的行数=六年级总人数(一定),即每行站的人数和站的行数的乘积一定,所以每行站的人数和站的行数成反比例关系。
【点睛】本题主要考查辨识成正比例的量和成反比例的量。
9. 5 10
【分析】根据题目可知,重物的重量与弹簧伸长的长度成正比例,同时挂60克的重物,弹簧的长度为7厘米,当挂上120克重物的时候,弹簧长度为9厘米,由此即可知道当弹簧多挂120-60=60克的重物的时候,弹簧伸长了9-7=2厘米,即60克伸长2厘米,则伸长1厘米对应的是60÷2=30克,由于挂60克伸长2厘米后是7厘米,原来是7-2=5厘米;当挂上150厘米,弹簧伸长:150÷30=5厘米,则弹簧长度:5+5=10厘米。
【详解】根据题意,弹簧每伸长1厘米,需要挂的重物的重量是:
(120-60)÷(9-7)
=60÷2
=30(克)
重物的重量与弹簧伸长成正比例
30克对应1厘米,60克对应弹簧伸长的厘米数是:
1×(60÷30)
=1×2
=2(厘米)
7-2=5(厘米)
1×(150÷30)+5
=1×5+5
=5+5
=10(厘米)
【点睛】本题考查正比例的应用,根据正比例的意义,进行解答问题。
10. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
11. 640 12
【分析】根据题意可知:除草剂÷种植农作物的面积=施药量(一定),即:除草剂和种植农作物的面积的比值一定,成正比例关系,据此列比例解答。
【详解】解:设在16公顷的棉花地喷洒这种除草剂,需除草剂x毫升。
x∶16=40∶1
x=16×40
x=640
设若有720毫升的除草剂,可以喷洒y公顷的玉米地。
720∶y=60∶1
60y=720
y=12
【点睛】解答此题的关键是:先判断题中的两种相关联的量成什么比例,并找准对应量。
12. 1∶20 4∶3
【分析】用小青照片中的身高比实际的身高,即可求出照片是把人按什么比缩小的;照片是按相同的比例将妈妈和小青的身高缩小的,所以根据实际高度写出妈妈和小青的身高比即可。
【详解】6厘米∶1.2米
=6厘米∶120厘米
=1∶20;
这张照片是把人按1∶20的比缩小的;
照片中妈妈和小青的身高比是1.6∶1.2=4∶3。
【点睛】明确图形放大与缩小中比的意义是解答本题的关键,比的前项表示变化后图形的边长,比的后项表示变化前图形的边长。
13.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为已走的路程+剩下的路程=总路程(一定),是和一定,
所以已走的路程和剩下的路程不成反比例;
故答案为:×
14.×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】由分析可得:xy+2=k(一定),即xy=k-2(一定),是乘积一定,则x和y成反比例,所以原题说法错误。
故答案为:×
15.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定。如果是比值一定,就成正比例;如果是乘积一定,则成反比例;如果比值和乘积都不一定,则不成比例。
【详解】圆的周长=2×π×半径
圆的周长÷它的半径=2π,是比值一定
所以圆的半径和周长成正比例,原题干说法正确
故答案为:√
【点睛】本题考查正比例和反比例的意义及辨识,根据正比例和反比例的意义进行解答。
16.×
【分析】判断圆的半径和面积是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果是比值不一定,就不成正比例。
【详解】圆的面积÷半径=圆周率×半径(不一定),是比值不一定,圆的半径和面积不成正比例。
故答案为:×
【点睛】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断。
17.√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例;据此进行判断。
【详解】若ab-8=125,即ab=133,是乘积一定,则a与b成反比例;
原题说法正确。
故答案为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
18.39吨
【分析】根据题意知道,海水的质量和盐的质量的比值一定,所以海水的质量和盐的质量成正比例,由此列式解答即可。
【详解】解:设可以晒出x吨盐。
100∶6=650∶x
100x=6×650
100x=3900
100x÷100=3900÷100
x=39
答:可以晒出39吨盐。
19.1千克
【分析】设x多少千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量,已知50克黄豆的蛋白质含量相当于600克牛奶的蛋白质含量,列出正比例算式解答即可。
【详解】600克=0.6千克 50克=0.05千克
解:设x千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量。
0.05∶0.6=x∶12
0.6x=0.05×12
0.6x=0.6
0.6x÷0.6=0.6÷0.6
x=1
答:1千克黄豆的蛋白质含量相当于12千克牛奶的蛋白质含量。
20.54块
【分析】根据题意,一块方砖的面积×方砖的块数=这间房子地面的面积(一定),所以一块方砖的面积与方砖的块数成反比例。由此设需用x块,列出比例式(8×8)×x=96×36即可解决问题。
【详解】解:设需要x块砖。
(8×8)×x=96×36
64x=3456
64x÷64=3456÷64
x=54
答:需要54块。
21.24个
【分析】
每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。设需要x个小正方形,长方形彩纸的面积=36×需要小正方形个数,由此解答即可。
【详解】
解:设需要x个小正方形。
36x=216×4
36x=864
36x÷x=864÷36
x=24
答:需要24个小正方形。
22.(1)正;1∶300000
(2)0.6小时
【分析】
(1)正比例图像是一条经过原点的直线,观察图像即可确定比例关系;根据图上距离∶实际距离=比例尺,写出图上距离与实际距离的比,化简即可。
(2)根据实际距离=图上距离÷比例尺,求出中心公园到市博物馆的实际距离,再根据时间=路程÷速度,列式解答即可。
【详解】(1)1厘米∶3千米=1厘米∶300000厘米=1∶300000
图上距离和实际距离成正比例关系。这幅地图的比例尺是1∶300000。
(2)(厘米)
2400000厘米=24千米
24÷40=0.6(小时)
答:需要0.6小时。
23.(1)正比例
(2)见详解
(3)4.5;20
【分析】
(1)结合统计表中的数据,用=单价,发现单价一定,即比值一定,据此得出充电的费用与充电量成正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
(2)根据统计表中的数据,先在图中描出表示费用与充电量相对应的点,然后把它们按顺序连起来,完成正比例图象的绘制。
(3)由图象可知,电的单价是2元,求9元可以充电多少千瓦·时,根据“总价÷单价=数量”解答;求想充10千瓦·时的电,需要花多少元钱,根据“单价×数量=总价”解答。
【详解】(1)===…=2(一定)
比值一定,则充电的费用与充电量成正比例关系。
(2)如图:
(3)9÷2=4.5(千瓦·时)
2×10=20(元)
根据图象,9元可以充电4.5千瓦·时;若妈妈想充10千瓦·时的电,需要花20元钱。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
