人教版六年级下册数学 《比例的基本性质》(课件)(共40张PPT)
文档属性
| 名称 | 人教版六年级下册数学 《比例的基本性质》(课件)(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 17:11:44 | ||
图片预览








文档简介
(共40张PPT)
比例的基本性质
人教版小学数学六年级下册第四单元
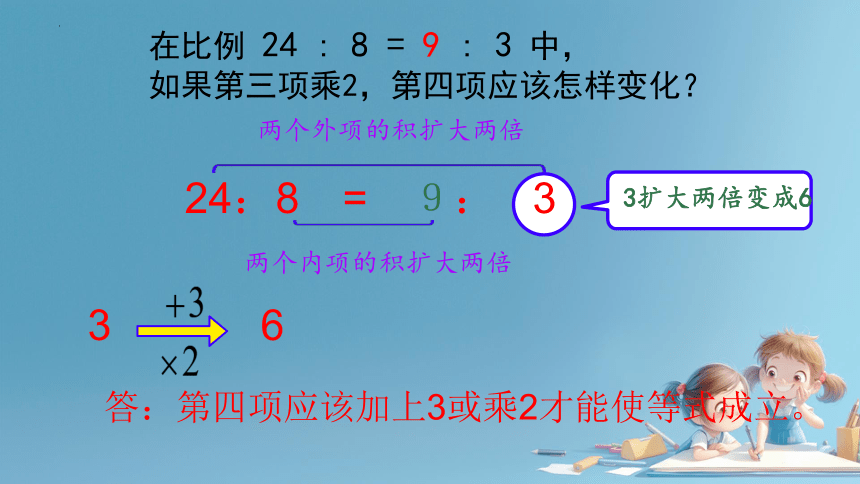
在比例 24 : 8 = 9 : 3 中,
如果第三项乘2,第四项应该怎样变化?
24:8=18:( )
答:第四项应该加上3或乘2才能使等式成立。
3
6
在比例 24 : 8 = 9 : 3 中,
如果第三项乘2,第四项应该怎样变化?
24:8 = 9: 3
答:第四项应该加上3或乘2才能使等式成立。
3
6
两个内项的积扩大两倍
两个外项的积扩大两倍
3扩大两倍变成6
复习回顾
因为2=2
所有4:2=5:2.5
表示两个比相等的式子叫做比例。
判断下面的比能否组成比例
(1)4:2和5:2.5
利用比例的意义进行判断
学习目标
2.我能根据比例的基本性质判断两个比能否组成比例。
1.我能认识比例的各部分的名称。
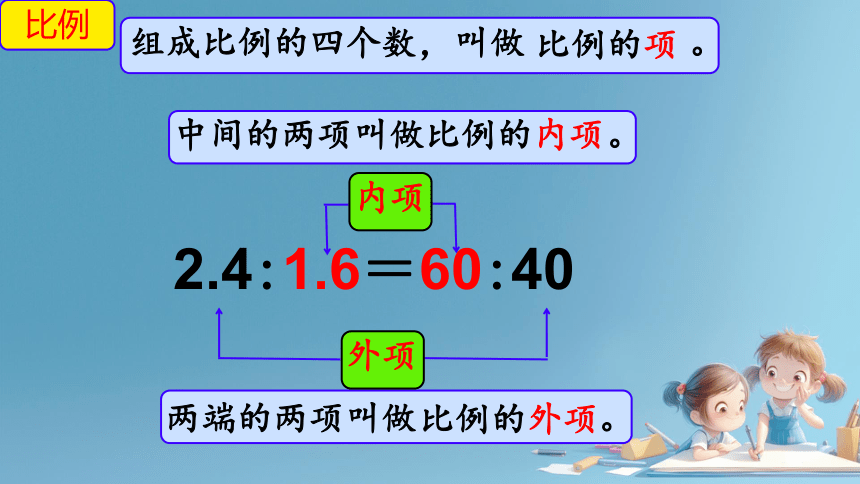
2.4:1.6=60:40
比例
组成比例的四个数,叫做 。
两端的两项叫做 。
外项
中间的两项叫做 。
内项
比例的项
比例的内项
比例的外项
找出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
外项
内项
外项
内项
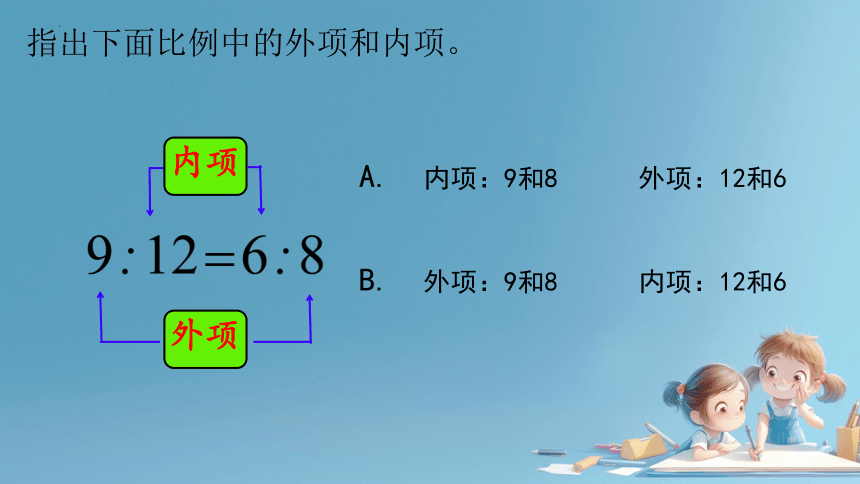
指出下面比例中的外项和内项。
外项
内项
A. 内项:9和8 外项:12和6
B. 外项:9和8 内项:12和6
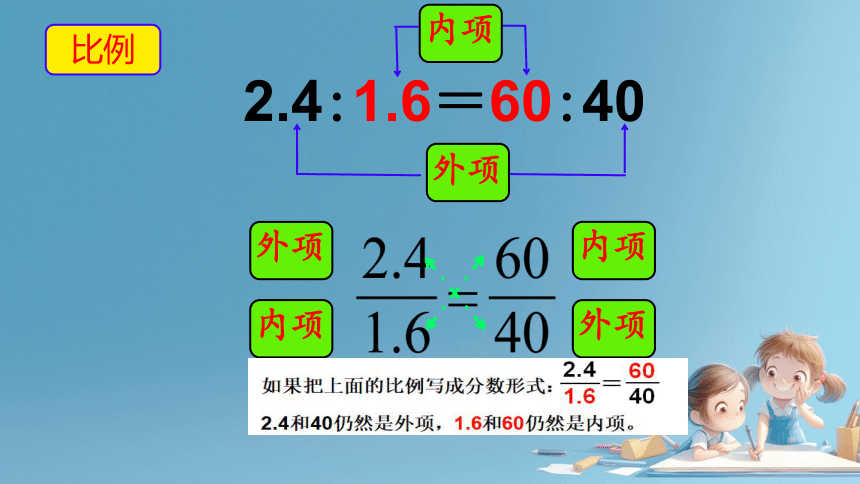
比例
外项
外项
内项
内项
2.4:1.6=60:40
外项
内项
指出下面比例中的外项和内项。
外项
外项
内项
内项
A. 内项是4.5和5 外项是1.5和15
B. 外项是4.5和5 内项是1.5和15
计算下面比例中两个外项的积和两个内项的积
(1)2.4:1.6=60:40
2.4×40=96
1.6×60=96
3×15=
45
5×9= 45
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
试一试 1
5
0.2
1
2
3
5
8︰25=40︰125
试一试
A. 8 ×125=25×40
B. 8 ×40 =25 ×125
巩固练习
1.应用比例的基本性质,判断下面每组中的两个比能否组成比例?
(1) 6:3 和 8:5
(2) 0.2 : 2.5 和 4 : 50
A.能组成比例。
B.不能给成比例。
第二课时
比例的基本性质
6 ,9 , 10 和( )可以组成比例。
A 7 B 5.4 C 1.5 D66
能与 : 组成比例的比是( )
A 2:3 B 4:6 C 6:9 D 3:2
比例
外项
外项
内项
内项
2.4:1.6=60:40
外项
内项
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
比例的基本性质
两个外项的积等于两个内项的积。
=bc
A.能组成比例。
B.不能给成比例。
A.能组成比例。
B.不能给成比例。
(5)判断
5x=6y,x:y=5:6( )
A.√ B.×
6. 6 a = 7 b,则 a : b = ( ) : ( )
A 6 : 7 B 7 : 6
6a
7b
6
7
=
a和8是外项
b和5是内项
7. 若 = ,则 a : b = ( ) : ( )
8.在一个比例中,两个比的比值都等于2,这个比例的外项
是8和9,则这个比例是( )。
( ):( )=( ):( )
8
9
2
2
4
18
8÷2=4
9×2=18
9.在一个比例中,两个比的比值都是 ,两个外项分别
是17和 ,请把这个比例写出来。
( ):( )=( ):( )
17
(10).在括号里填上合适的数,使比例成立。
100
100
20
(11). 如果3a=4b,那么
a:b=( ):( )
如果
3
4
5
6
12.一个比例的两个外项互为倒数,这个比例的两个内项
的积一定是( )。
( ):( )=( ):( )
1
1
13.一个比例的两个外项互为倒数,如果一个内项是 ,
那么另一个内项是( )
两个内项的乘积也是1, ×( )=1
两个外项互为倒数,两外项的乘积是1
3×40=8×15
3 : = : 40
8
15
3 : = :40
15
8
40: = :3
8
15
40: = :3
15
8
8: = :15
3
40
8: = :15
40
3
15: = :8
3
40
15: = :8
40
3
16.根据比例24:8=9:3回答下列问题。
(1)如果第一项24减6,第二项变成几才能使等式成立?
24-6=18
18:( )=9:3
答:第二项变成6才能使等式成立。
课堂回顾
前项:2
后项:5
比值:0.4
外项:2、10
内项:5、4
2个数组成,是个式子
4个数组成,是个等式
两个数相除,
又叫做两个数的比
表示两个比相等
的式子叫做比例
比的前项和后项同时
乘或除以相同的数
(0除外),比值不变
在比例里,
两个外项的积等于
两个内项的积
比较一下,你能发现什么?
3×15=
45
5×9= 45
在比例里,两个外项的积等于两个内项的积。
3×15=5×9
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
交叉相乘
2.4×40=1.6×60
2.4
1.6
=
60
40
2.4:1.6= 60:40
外项
内项
2.4×40=1.6×60
9. 如果a×3 = b×4,则:
4
4
a :( )= ( ): 3
b
b
4
4
b
b
3
3
a
a
3
3
a
a
3 :( )= ( ): a
b :( )= ( ): 4
4 :( )= ( ): b
a :( )= ( ): 3
3 :( )= ( ): a
b :( )= ( ): 4
4 :( )= ( ): b
把a和3看成外项
把b和4看成外项
优翼
4.已知24×3=8×9,根据比例的基本性质,你能写出比例吗?你能写几个?
5. 把8、40和20再配上一个数组成比例,这个数可以是多少?
6、填空:
(1)在a:7=9:b中,( )是内项,( )是外项,a×b=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的积是( ),两个外项可能是( )和( )或( )和( )。
(3)在一个比例里,两个外项互为倒数,那么两个内项的积是( ),如果一个外项是 ,另一个外项是( )。
7、9
a、b
63
24
1
2
12
4
6
5.根据 写比例。
1.4
2.5
0.4
2.5
1.4
商不变的规律
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的分子和分母同时乘或除以相同的数
(0除外),分数的大小不变。
比的基本性质
比的前项和后项同时乘或除以相同的数(0除外)比值不变。
比例的基本性质
两个外项的积等于两个内项的积。
比例的基本性质
人教版小学数学六年级下册第四单元
在比例 24 : 8 = 9 : 3 中,
如果第三项乘2,第四项应该怎样变化?
24:8=18:( )
答:第四项应该加上3或乘2才能使等式成立。
3
6
在比例 24 : 8 = 9 : 3 中,
如果第三项乘2,第四项应该怎样变化?
24:8 = 9: 3
答:第四项应该加上3或乘2才能使等式成立。
3
6
两个内项的积扩大两倍
两个外项的积扩大两倍
3扩大两倍变成6
复习回顾
因为2=2
所有4:2=5:2.5
表示两个比相等的式子叫做比例。
判断下面的比能否组成比例
(1)4:2和5:2.5
利用比例的意义进行判断
学习目标
2.我能根据比例的基本性质判断两个比能否组成比例。
1.我能认识比例的各部分的名称。
2.4:1.6=60:40
比例
组成比例的四个数,叫做 。
两端的两项叫做 。
外项
中间的两项叫做 。
内项
比例的项
比例的内项
比例的外项
找出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
外项
内项
外项
内项
指出下面比例中的外项和内项。
外项
内项
A. 内项:9和8 外项:12和6
B. 外项:9和8 内项:12和6
比例
外项
外项
内项
内项
2.4:1.6=60:40
外项
内项
指出下面比例中的外项和内项。
外项
外项
内项
内项
A. 内项是4.5和5 外项是1.5和15
B. 外项是4.5和5 内项是1.5和15
计算下面比例中两个外项的积和两个内项的积
(1)2.4:1.6=60:40
2.4×40=96
1.6×60=96
3×15=
45
5×9= 45
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
试一试 1
5
0.2
1
2
3
5
8︰25=40︰125
试一试
A. 8 ×125=25×40
B. 8 ×40 =25 ×125
巩固练习
1.应用比例的基本性质,判断下面每组中的两个比能否组成比例?
(1) 6:3 和 8:5
(2) 0.2 : 2.5 和 4 : 50
A.能组成比例。
B.不能给成比例。
第二课时
比例的基本性质
6 ,9 , 10 和( )可以组成比例。
A 7 B 5.4 C 1.5 D66
能与 : 组成比例的比是( )
A 2:3 B 4:6 C 6:9 D 3:2
比例
外项
外项
内项
内项
2.4:1.6=60:40
外项
内项
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
比例的基本性质
两个外项的积等于两个内项的积。
=bc
A.能组成比例。
B.不能给成比例。
A.能组成比例。
B.不能给成比例。
(5)判断
5x=6y,x:y=5:6( )
A.√ B.×
6. 6 a = 7 b,则 a : b = ( ) : ( )
A 6 : 7 B 7 : 6
6a
7b
6
7
=
a和8是外项
b和5是内项
7. 若 = ,则 a : b = ( ) : ( )
8.在一个比例中,两个比的比值都等于2,这个比例的外项
是8和9,则这个比例是( )。
( ):( )=( ):( )
8
9
2
2
4
18
8÷2=4
9×2=18
9.在一个比例中,两个比的比值都是 ,两个外项分别
是17和 ,请把这个比例写出来。
( ):( )=( ):( )
17
(10).在括号里填上合适的数,使比例成立。
100
100
20
(11). 如果3a=4b,那么
a:b=( ):( )
如果
3
4
5
6
12.一个比例的两个外项互为倒数,这个比例的两个内项
的积一定是( )。
( ):( )=( ):( )
1
1
13.一个比例的两个外项互为倒数,如果一个内项是 ,
那么另一个内项是( )
两个内项的乘积也是1, ×( )=1
两个外项互为倒数,两外项的乘积是1
3×40=8×15
3 : = : 40
8
15
3 : = :40
15
8
40: = :3
8
15
40: = :3
15
8
8: = :15
3
40
8: = :15
40
3
15: = :8
3
40
15: = :8
40
3
16.根据比例24:8=9:3回答下列问题。
(1)如果第一项24减6,第二项变成几才能使等式成立?
24-6=18
18:( )=9:3
答:第二项变成6才能使等式成立。
课堂回顾
前项:2
后项:5
比值:0.4
外项:2、10
内项:5、4
2个数组成,是个式子
4个数组成,是个等式
两个数相除,
又叫做两个数的比
表示两个比相等
的式子叫做比例
比的前项和后项同时
乘或除以相同的数
(0除外),比值不变
在比例里,
两个外项的积等于
两个内项的积
比较一下,你能发现什么?
3×15=
45
5×9= 45
在比例里,两个外项的积等于两个内项的积。
3×15=5×9
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
交叉相乘
2.4×40=1.6×60
2.4
1.6
=
60
40
2.4:1.6= 60:40
外项
内项
2.4×40=1.6×60
9. 如果a×3 = b×4,则:
4
4
a :( )= ( ): 3
b
b
4
4
b
b
3
3
a
a
3
3
a
a
3 :( )= ( ): a
b :( )= ( ): 4
4 :( )= ( ): b
a :( )= ( ): 3
3 :( )= ( ): a
b :( )= ( ): 4
4 :( )= ( ): b
把a和3看成外项
把b和4看成外项
优翼
4.已知24×3=8×9,根据比例的基本性质,你能写出比例吗?你能写几个?
5. 把8、40和20再配上一个数组成比例,这个数可以是多少?
6、填空:
(1)在a:7=9:b中,( )是内项,( )是外项,a×b=( )。
(2)一个比例的两个内项分别是3和8,则两个外项的积是( ),两个外项可能是( )和( )或( )和( )。
(3)在一个比例里,两个外项互为倒数,那么两个内项的积是( ),如果一个外项是 ,另一个外项是( )。
7、9
a、b
63
24
1
2
12
4
6
5.根据 写比例。
1.4
2.5
0.4
2.5
1.4
商不变的规律
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的分子和分母同时乘或除以相同的数
(0除外),分数的大小不变。
比的基本性质
比的前项和后项同时乘或除以相同的数(0除外)比值不变。
比例的基本性质
两个外项的积等于两个内项的积。
