8.3.1棱柱、棱锥、棱台的表面积和体积 学案
文档属性
| 名称 | 8.3.1棱柱、棱锥、棱台的表面积和体积 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 519.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 10:26:43 | ||
图片预览

文档简介
2023~2024学年高一下学期 数学必修第二册导学案 编号:038
8.3.1棱柱、棱锥、棱台的表面积和体积
班级 姓名
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积与体积的求法.
2.会求与棱柱、棱锥、棱台有关的组合体的表面积与体积.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 一、棱柱、棱锥、棱台的表面积图形表面积多面体 INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET 多面体的表面积就是围成多面体各个面的面积的和,也就是 的面积
阅读教材,完成右边的内容 二、棱柱、棱锥、棱台的体积几何体体积说明棱柱V棱柱= S为棱柱的底面积,h为棱柱的高棱锥V棱锥= S为棱锥的底面积,h为棱锥的高棱台V棱台= S′,S分别为棱台的上、下底面面积,h为棱台的高
棱柱、棱锥、棱台的表面积 例1、如图是一个搭建好的帐篷,它的下部是一个正六棱柱,上部是一个正六棱锥,其中帐篷的高为PO,正六棱锥的高为PO1,且PO=3PO1.当PO1=2 m,PA1=4 m时,求帐篷的表面积.变式1、(1)侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是 (2)现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,则该直四棱柱的侧面积为________.
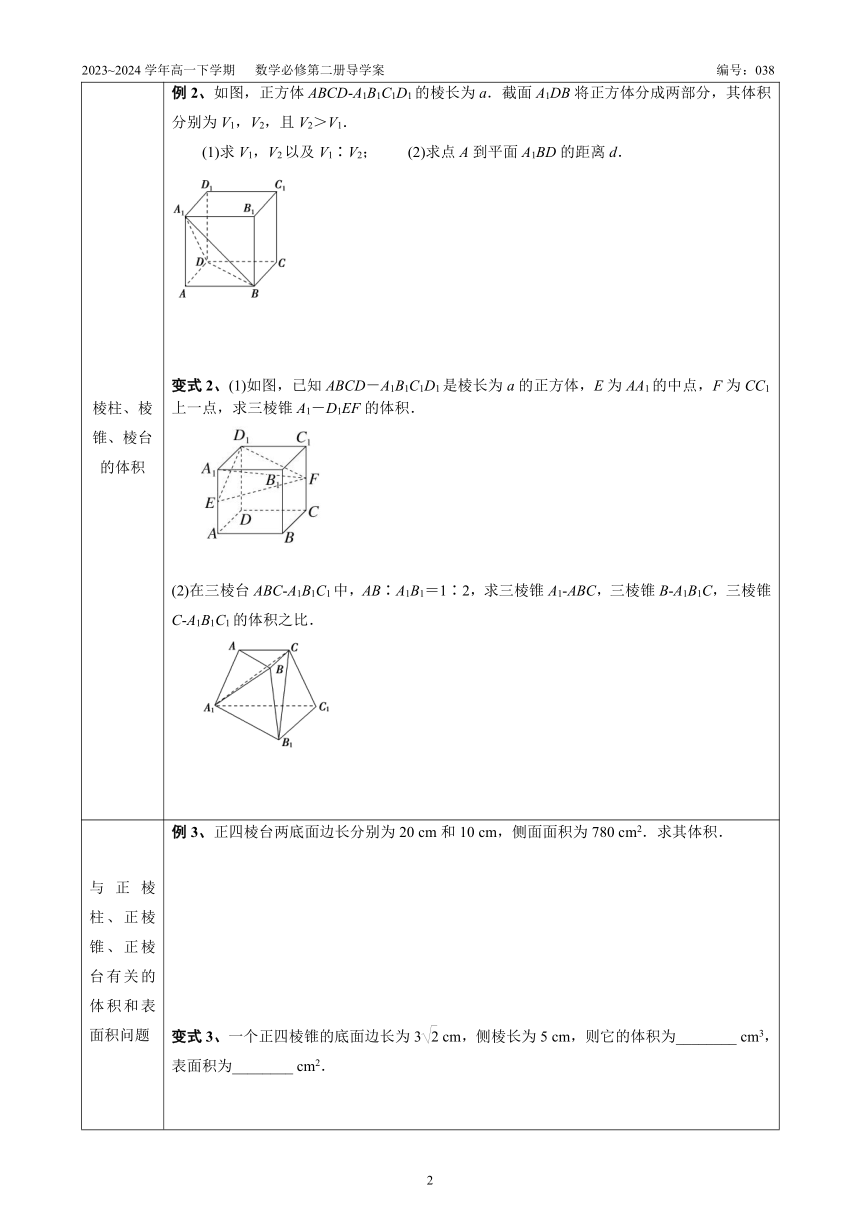
棱柱、棱锥、棱台的体积 例2、如图,正方体ABCD A1B1C1D1的棱长为a.截面A1DB将正方体分成两部分,其体积分别为V1,V2,且V2>V1.(1)求V1,V2以及V1∶V2; (2)求点A到平面A1BD的距离d.变式2、(1)如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.(2)在三棱台ABC A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1 ABC,三棱锥B A1B1C,三棱锥C A1B1C1的体积之比.
与正棱柱、正棱锥、正棱台有关的体积和表面积问题 例3、正四棱台两底面边长分别为20 cm和10 cm,侧面面积为780 cm2.求其体积.变式3、一个正四棱锥的底面边长为3 cm,侧棱长为5 cm,则它的体积为________ cm3,表面积为________ cm2.
课后作业
一、基础训练题
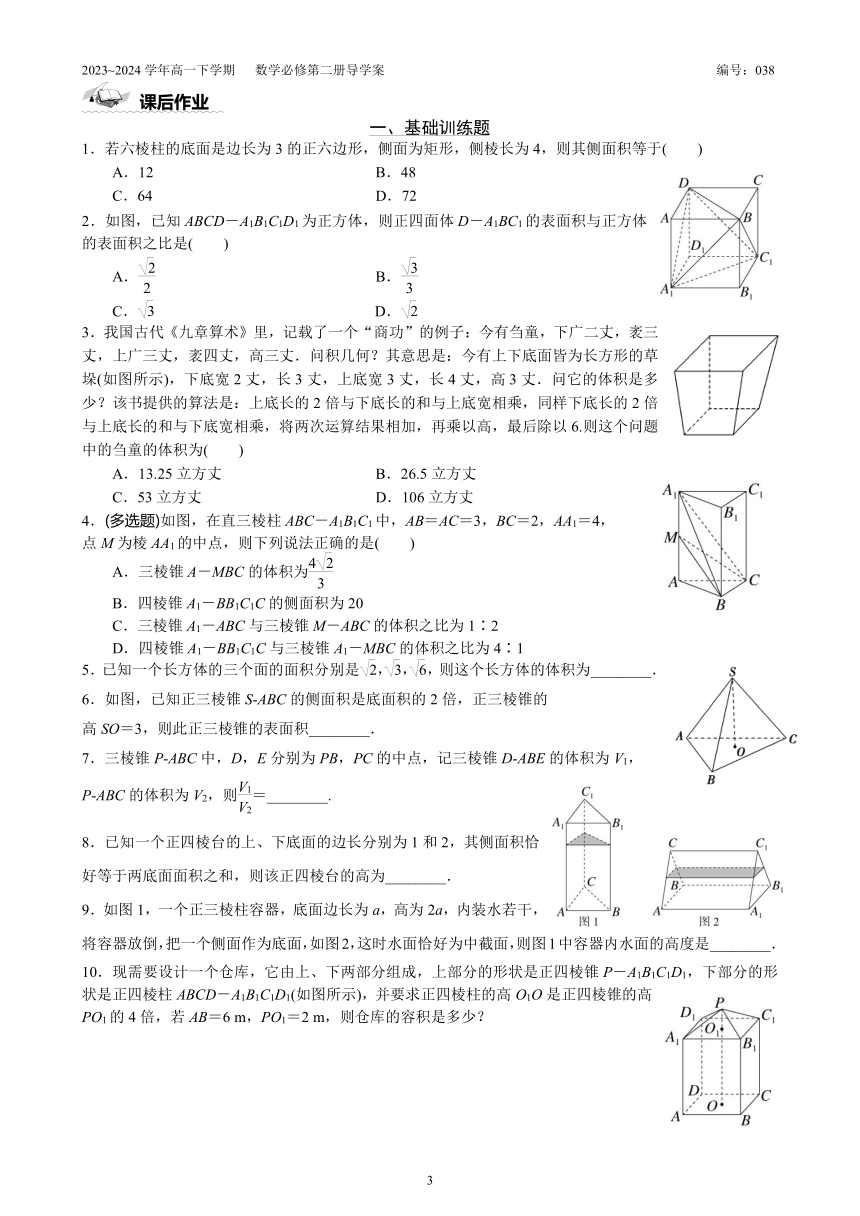
1.若六棱柱的底面是边长为3的正六边形,侧面为矩形,侧棱长为4,则其侧面积等于( )
A.12 B.48
C.64 D.72
2.如图,已知ABCD-A1B1C1D1为正方体,则正四面体D-A1BC1的表面积与正方体的表面积之比是( )
A. B.
C. D.
3.我国古代《九章算术》里,记载了一个“商功”的例子:今有刍童,下广二丈,袤三丈,上广三丈,袤四丈,高三丈.问积几何?其意思是:今有上下底面皆为长方形的草垛(如图所示),下底宽2丈,长3丈,上底宽3丈,长4丈,高3丈.问它的体积是多少?该书提供的算法是:上底长的2倍与下底长的和与上底宽相乘,同样下底长的2倍与上底长的和与下底宽相乘,将两次运算结果相加,再乘以高,最后除以6.则这个问题中的刍童的体积为( )
A.13.25立方丈 B.26.5立方丈
C.53立方丈 D.106立方丈
4.(多选题)如图,在直三棱柱ABC-A1B1C1中,AB=AC=3,BC=2,AA1=4,
点M为棱AA1的中点,则下列说法正确的是( )
A.三棱锥A-MBC的体积为
B.四棱锥A1-BB1C1C的侧面积为20
C.三棱锥A1-ABC与三棱锥M-ABC的体积之比为1∶2
D.四棱锥A1-BB1C1C与三棱锥A1-MBC的体积之比为4∶1
5.已知一个长方体的三个面的面积分别是,,,则这个长方体的体积为________.
6.如图,已知正三棱锥S ABC的侧面积是底面积的2倍,正三棱锥的
高SO=3,则此正三棱锥的表面积________.
7.三棱锥P ABC中,D,E分别为PB,PC的中点,记三棱锥D ABE的体积为V1,
P ABC的体积为V2,则=________.
8.已知一个正四棱台的上、下底面的边长分别为1和2,其侧面积恰好等于两底面面积之和,则该正四棱台的高为________.
9.如图1,一个正三棱柱容器,底面边长为a,高为2a,内装水若干,将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面,则图1中容器内水面的高度是________.
10.现需要设计一个仓库,它由上、下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍,若AB=6 m,PO1=2 m,则仓库的容积是多少?
11.已知正六棱锥被过高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥PO的侧棱长为12 cm,小棱锥的底面边长为4 cm,求截得的棱台的侧面积和表面积.
二、综合训练题
12.鲁班锁起源于中国古代建筑的榫卯结构.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.图1是一个鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁玩具的表面积为( )
图1 图2
A.8(6+6+) B.6(8+8+)
C.8(6+6+) D.6(8+8+)
13.(多选题)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱AA1,CC1的中点,以下结论正确的是( )
A.V三棱锥B1-EFB=V三棱锥B1-EFD1
B.四棱锥B1-EBFD1为正四棱锥
C.四棱锥B1-EBFD1的体积为
D.多面体BCDD1EF的体积为
三、能力提升题
14.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的表面积为( )
A. B.2 C. D.
15.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
16.如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
8.3.1棱柱、棱锥、棱台的表面积和体积
参考答案
1、【答案】D 【解析】该六棱柱的6个侧面是全等的矩形,则S侧=6×(3×4)=72.
2、【答案】B
【解析】设正方体的棱长为1,则正方体的表面积为6,正四面体D-A1BC1的棱长为,
表面积为4××sin 60°×=2,∴正四面体D-A1BC1的表面积与正方体的表面积之比是.
3、【答案】B
【解析】由题意知,刍童的体积为[(4×2+3)×3+(3×2+4)×2]×3÷6=26.5(立方丈).
4、【答案】AD
【解析】依题意,△ABC的底边BC上的高为=2,面积S=×2×2=2,
故V三棱锥A-MBC=V三棱锥M-ABC=S·MA=×2×2=,故A正确;
四棱锥A1-BB1C1C的侧面积为S侧=S△A1B1C1+S△A1BC+S△A1B1B+S△A1C1C
=2+×2×+3×4=2+2+12,故B错误;
由三棱锥A1-ABC与三棱锥M-ABC同底,得其体积之比为=2,故C错误;
因为V四棱锥A1-BB1C1C=V三棱柱ABC-A1B1C1-V三棱锥A1-ABC
=S·AA1-S·AA1=S·AA1,V三棱锥A1-MBC=V三棱锥A1-ABC-V三棱锥M-ABC
=S·AA1-S·AA1=S·AA1,则=S·AA1×=4,故D正确.
5、【答案】
【解析】设三条棱长分别为a,b,c,则三式相乘得(abc)2=6,故长方体的体积V=abc=.
6、【答案】27
【解析】如图,设正三棱锥的底面边长为a,斜高为h′,过点O作OE⊥AB,
与AB交于点E,连接SE,则SE⊥AB,SE=h′.
∵S侧=2S底,∴·3a·h′=a2×2,∴a=h′.∵SO⊥OE,∴SO2+OE2=SE2.
∴32+=h′2.∴h′=2,∴a=h′=6.
∴S底=a2=×62=9,S侧=2S底=18,∴S表=S侧+S底=18+9=27.
7、【答案】
【解析】如图,设点C到平面PAB的距离为h,三角形PAB的面积为S,
则V2=Sh,V1=VE ADB=×S×h=Sh,所以=.
8、【答案】
【解析】设正四棱台的高、斜高分别为h,h′.由题意得,4××(1+2)×h′=12+22,解得h′=.
根据棱台的高、斜高、边心距构成直角梯形,可得h2+,解得h=.
9、【答案】a
【解析】设题图1中容器内液面的高度为h,液体的体积为V,则V=S△ABCh.题图2中液体组成了一个直四棱柱,其底面积为S△ABC,高为2a,则V=S△ABC·2a,∴h==a.
10、【解】由PO1=2 m,知O1O=4PO1=8 m,因为A1B1=AB=6 m,
所以正四棱锥P-A1B1C1D1的体积V锥=·A1B12·PO1=×62×2=24(m3),正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·O1O=62×8=288(m3),所以仓库的容积V=V锥+V柱=24+288=312(m3).
11、【解】(1)由题意知S小棱锥侧∶S大棱锥侧=1∶4,则S大棱锥侧∶S小棱锥侧∶S棱台侧=4∶1∶3.
(2)∵小棱锥的底面边长为4 cm,∴大棱锥的底面边长为8 cm,又大棱锥的侧棱长为12 cm,
∴棱台的侧棱长为6 cm.
所以棱台的一个侧面的高h′==4(cm),∴S棱台侧=6××4=144(cm2),
∴S棱台表=S棱台侧+S上底+S下底=144+24+96=144+120(cm2).
12、【答案】A
【解析】由题图,可知该鲁班锁玩具可以看成是由一个棱长为2(1+)的正方体截去了8个正三棱锥而得到的,且被截去的正三棱锥的底面边长为2,侧棱长为,
则该鲁班锁玩具的表面积为6×[4×(1+)2-4×××]+8××2×=8(6+6+).
13、【答案】ACD
【解析】由已知得EB=BF=FD1=D1E=,D1F∥BE,则四边形EBFD1是菱形.
A中两个三棱锥等底同高,所以V三棱锥B1-EFB=V三棱锥B1-EFD1,故A正确;
明显底面EBFD1不是正方形,故B错误;
V四棱锥B1-EBFD1=2V三棱锥B1-EFB=2V三棱锥F-B1EB
=2×S△B1EB×2=2××2×2=,故C正确;
连接DE,BD,则多面体BCDD1EF的体积等于正方体体积的一半减去三棱锥B-ADE的体积,
即V=×2×2×2-××2×1×2=,故D正确.故选ACD.
14、【答案】B
【解析】所求凸多面体的表面积是两个底面
边长为1,高为的四棱锥的侧面积之和,如图,四棱锥的侧棱长l=,
所以,以该正方体各个面的中心为顶点的凸多面体的表面积S=8××1×1×sin 60°=2.
15、【答案】90 138
【解析】该几何体的体积V=4×6×3+×4×3×3=90,
表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.
16、【解】如图,连接EB,EC,AC,V四棱锥E-ABCD=×42×3=16.
∵AB=2EF,EF∥AB,∴S△EAB=2S△BEF,
∴V三棱锥F-EBC=V三棱锥C-EFB=V三棱锥C-ABE=V三棱锥E-ABC=×V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
PAGE
1
8.3.1棱柱、棱锥、棱台的表面积和体积
班级 姓名
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积与体积的求法.
2.会求与棱柱、棱锥、棱台有关的组合体的表面积与体积.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 一、棱柱、棱锥、棱台的表面积图形表面积多面体 INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-79.TIF" \* MERGEFORMATINET 多面体的表面积就是围成多面体各个面的面积的和,也就是 的面积
阅读教材,完成右边的内容 二、棱柱、棱锥、棱台的体积几何体体积说明棱柱V棱柱= S为棱柱的底面积,h为棱柱的高棱锥V棱锥= S为棱锥的底面积,h为棱锥的高棱台V棱台= S′,S分别为棱台的上、下底面面积,h为棱台的高
棱柱、棱锥、棱台的表面积 例1、如图是一个搭建好的帐篷,它的下部是一个正六棱柱,上部是一个正六棱锥,其中帐篷的高为PO,正六棱锥的高为PO1,且PO=3PO1.当PO1=2 m,PA1=4 m时,求帐篷的表面积.变式1、(1)侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是 (2)现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,则该直四棱柱的侧面积为________.
棱柱、棱锥、棱台的体积 例2、如图,正方体ABCD A1B1C1D1的棱长为a.截面A1DB将正方体分成两部分,其体积分别为V1,V2,且V2>V1.(1)求V1,V2以及V1∶V2; (2)求点A到平面A1BD的距离d.变式2、(1)如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E为AA1的中点,F为CC1上一点,求三棱锥A1-D1EF的体积.(2)在三棱台ABC A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1 ABC,三棱锥B A1B1C,三棱锥C A1B1C1的体积之比.
与正棱柱、正棱锥、正棱台有关的体积和表面积问题 例3、正四棱台两底面边长分别为20 cm和10 cm,侧面面积为780 cm2.求其体积.变式3、一个正四棱锥的底面边长为3 cm,侧棱长为5 cm,则它的体积为________ cm3,表面积为________ cm2.
课后作业
一、基础训练题
1.若六棱柱的底面是边长为3的正六边形,侧面为矩形,侧棱长为4,则其侧面积等于( )
A.12 B.48
C.64 D.72
2.如图,已知ABCD-A1B1C1D1为正方体,则正四面体D-A1BC1的表面积与正方体的表面积之比是( )
A. B.
C. D.
3.我国古代《九章算术》里,记载了一个“商功”的例子:今有刍童,下广二丈,袤三丈,上广三丈,袤四丈,高三丈.问积几何?其意思是:今有上下底面皆为长方形的草垛(如图所示),下底宽2丈,长3丈,上底宽3丈,长4丈,高3丈.问它的体积是多少?该书提供的算法是:上底长的2倍与下底长的和与上底宽相乘,同样下底长的2倍与上底长的和与下底宽相乘,将两次运算结果相加,再乘以高,最后除以6.则这个问题中的刍童的体积为( )
A.13.25立方丈 B.26.5立方丈
C.53立方丈 D.106立方丈
4.(多选题)如图,在直三棱柱ABC-A1B1C1中,AB=AC=3,BC=2,AA1=4,
点M为棱AA1的中点,则下列说法正确的是( )
A.三棱锥A-MBC的体积为
B.四棱锥A1-BB1C1C的侧面积为20
C.三棱锥A1-ABC与三棱锥M-ABC的体积之比为1∶2
D.四棱锥A1-BB1C1C与三棱锥A1-MBC的体积之比为4∶1
5.已知一个长方体的三个面的面积分别是,,,则这个长方体的体积为________.
6.如图,已知正三棱锥S ABC的侧面积是底面积的2倍,正三棱锥的
高SO=3,则此正三棱锥的表面积________.
7.三棱锥P ABC中,D,E分别为PB,PC的中点,记三棱锥D ABE的体积为V1,
P ABC的体积为V2,则=________.
8.已知一个正四棱台的上、下底面的边长分别为1和2,其侧面积恰好等于两底面面积之和,则该正四棱台的高为________.
9.如图1,一个正三棱柱容器,底面边长为a,高为2a,内装水若干,将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面,则图1中容器内水面的高度是________.
10.现需要设计一个仓库,它由上、下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍,若AB=6 m,PO1=2 m,则仓库的容积是多少?
11.已知正六棱锥被过高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥PO的侧棱长为12 cm,小棱锥的底面边长为4 cm,求截得的棱台的侧面积和表面积.
二、综合训练题
12.鲁班锁起源于中国古代建筑的榫卯结构.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.图1是一个鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁玩具的表面积为( )
图1 图2
A.8(6+6+) B.6(8+8+)
C.8(6+6+) D.6(8+8+)
13.(多选题)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别为棱AA1,CC1的中点,以下结论正确的是( )
A.V三棱锥B1-EFB=V三棱锥B1-EFD1
B.四棱锥B1-EBFD1为正四棱锥
C.四棱锥B1-EBFD1的体积为
D.多面体BCDD1EF的体积为
三、能力提升题
14.若正方体的棱长为,则以该正方体各个面的中心为顶点的凸多面体的表面积为( )
A. B.2 C. D.
15.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.
16.如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
8.3.1棱柱、棱锥、棱台的表面积和体积
参考答案
1、【答案】D 【解析】该六棱柱的6个侧面是全等的矩形,则S侧=6×(3×4)=72.
2、【答案】B
【解析】设正方体的棱长为1,则正方体的表面积为6,正四面体D-A1BC1的棱长为,
表面积为4××sin 60°×=2,∴正四面体D-A1BC1的表面积与正方体的表面积之比是.
3、【答案】B
【解析】由题意知,刍童的体积为[(4×2+3)×3+(3×2+4)×2]×3÷6=26.5(立方丈).
4、【答案】AD
【解析】依题意,△ABC的底边BC上的高为=2,面积S=×2×2=2,
故V三棱锥A-MBC=V三棱锥M-ABC=S·MA=×2×2=,故A正确;
四棱锥A1-BB1C1C的侧面积为S侧=S△A1B1C1+S△A1BC+S△A1B1B+S△A1C1C
=2+×2×+3×4=2+2+12,故B错误;
由三棱锥A1-ABC与三棱锥M-ABC同底,得其体积之比为=2,故C错误;
因为V四棱锥A1-BB1C1C=V三棱柱ABC-A1B1C1-V三棱锥A1-ABC
=S·AA1-S·AA1=S·AA1,V三棱锥A1-MBC=V三棱锥A1-ABC-V三棱锥M-ABC
=S·AA1-S·AA1=S·AA1,则=S·AA1×=4,故D正确.
5、【答案】
【解析】设三条棱长分别为a,b,c,则三式相乘得(abc)2=6,故长方体的体积V=abc=.
6、【答案】27
【解析】如图,设正三棱锥的底面边长为a,斜高为h′,过点O作OE⊥AB,
与AB交于点E,连接SE,则SE⊥AB,SE=h′.
∵S侧=2S底,∴·3a·h′=a2×2,∴a=h′.∵SO⊥OE,∴SO2+OE2=SE2.
∴32+=h′2.∴h′=2,∴a=h′=6.
∴S底=a2=×62=9,S侧=2S底=18,∴S表=S侧+S底=18+9=27.
7、【答案】
【解析】如图,设点C到平面PAB的距离为h,三角形PAB的面积为S,
则V2=Sh,V1=VE ADB=×S×h=Sh,所以=.
8、【答案】
【解析】设正四棱台的高、斜高分别为h,h′.由题意得,4××(1+2)×h′=12+22,解得h′=.
根据棱台的高、斜高、边心距构成直角梯形,可得h2+,解得h=.
9、【答案】a
【解析】设题图1中容器内液面的高度为h,液体的体积为V,则V=S△ABCh.题图2中液体组成了一个直四棱柱,其底面积为S△ABC,高为2a,则V=S△ABC·2a,∴h==a.
10、【解】由PO1=2 m,知O1O=4PO1=8 m,因为A1B1=AB=6 m,
所以正四棱锥P-A1B1C1D1的体积V锥=·A1B12·PO1=×62×2=24(m3),正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·O1O=62×8=288(m3),所以仓库的容积V=V锥+V柱=24+288=312(m3).
11、【解】(1)由题意知S小棱锥侧∶S大棱锥侧=1∶4,则S大棱锥侧∶S小棱锥侧∶S棱台侧=4∶1∶3.
(2)∵小棱锥的底面边长为4 cm,∴大棱锥的底面边长为8 cm,又大棱锥的侧棱长为12 cm,
∴棱台的侧棱长为6 cm.
所以棱台的一个侧面的高h′==4(cm),∴S棱台侧=6××4=144(cm2),
∴S棱台表=S棱台侧+S上底+S下底=144+24+96=144+120(cm2).
12、【答案】A
【解析】由题图,可知该鲁班锁玩具可以看成是由一个棱长为2(1+)的正方体截去了8个正三棱锥而得到的,且被截去的正三棱锥的底面边长为2,侧棱长为,
则该鲁班锁玩具的表面积为6×[4×(1+)2-4×××]+8××2×=8(6+6+).
13、【答案】ACD
【解析】由已知得EB=BF=FD1=D1E=,D1F∥BE,则四边形EBFD1是菱形.
A中两个三棱锥等底同高,所以V三棱锥B1-EFB=V三棱锥B1-EFD1,故A正确;
明显底面EBFD1不是正方形,故B错误;
V四棱锥B1-EBFD1=2V三棱锥B1-EFB=2V三棱锥F-B1EB
=2×S△B1EB×2=2××2×2=,故C正确;
连接DE,BD,则多面体BCDD1EF的体积等于正方体体积的一半减去三棱锥B-ADE的体积,
即V=×2×2×2-××2×1×2=,故D正确.故选ACD.
14、【答案】B
【解析】所求凸多面体的表面积是两个底面
边长为1,高为的四棱锥的侧面积之和,如图,四棱锥的侧棱长l=,
所以,以该正方体各个面的中心为顶点的凸多面体的表面积S=8××1×1×sin 60°=2.
15、【答案】90 138
【解析】该几何体的体积V=4×6×3+×4×3×3=90,
表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.
16、【解】如图,连接EB,EC,AC,V四棱锥E-ABCD=×42×3=16.
∵AB=2EF,EF∥AB,∴S△EAB=2S△BEF,
∴V三棱锥F-EBC=V三棱锥C-EFB=V三棱锥C-ABE=V三棱锥E-ABC=×V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
PAGE
1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
