10.3.1 一元一次不等式的有关概念及解法习题课件(29张PPT)2023-2024学年冀教版数学七年级下册
文档属性
| 名称 | 10.3.1 一元一次不等式的有关概念及解法习题课件(29张PPT)2023-2024学年冀教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
10.3 解一元一次不等式
课时1 一元一次不等式的有关概念及解法
过基础 教材必备知识精练
知识点1 不等式的解及解集的概念
1. 是下列哪个不等式的解( )
A
A. B. C. D.
【解析】 把 分别代入不等式中,能使不等式成立的就是不等式的解,只有A选项中不等式成立.
【策略点拨】
判断某个数是不是不等式的解
用这个数代替不等式中的未知数,看不等式是否成立,若成立,则该数是不等式的一个解;若不成立,则该数不是不等式的解.
2.有下列4个结论:① 是不等式 的解;② 是不等式
的解集;③ 是不等式 的解;④ 是不等式
的解集.其中正确结论的序号是( )
D
A.①② B.①②③ C.③④ D.①③④
【解析】 对于①, 能使不等式 成立,所以 是不等式 的解;对于②,不等式 的解集是 ,虽然 可以使不等式 成立,但不是这个不等式的解的全体,所以不是不等式 的解集;对于③, 能使不等式 成立,所以 是不等式 的解;对于④, 是不等式 的解集.
知识点2 不等式的解集的表示
3.[2023沈阳中考]不等式 的解集在数轴上表示正确的是( )
B
A.&4& B.&5& C.&6& D.&7&
【归纳总结】
在数轴上表示不等式的解集的步骤
画出数轴 找到对应点 判断实心或空心(带等号实心,不带等
号空心) 判断方向(大于向右画,小于向左画) 画出解集.
4.教材P125A组T2变式一个不等式的解集在数轴上的表示
如图所示,则这个不等式可能是( )
A
A. B. C. D.
【解析】 处是空心圆圈,且折线向右, 这个不等式的解集为 , 这个不等式可能是 .
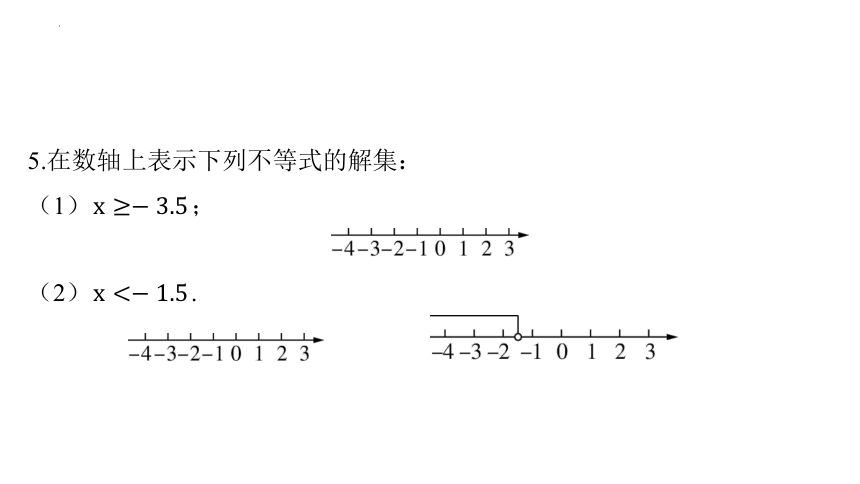
5.在数轴上表示下列不等式的解集:
(1) ;
(2) .
知识点3 一元一次不等式的概念
6.[2022吉安期末]给出下列式子:① ;② ;③ ;
④ ;⑤ .其中是一元一次不等式的有( )
B
A.1个 B.2个 C.3个 D.4个
【解析】 , 是一元一次不等式,共2个.
7.易错题[2023保定十七中期中]若 是关于 的一元一
次不等式.则 的值为( )
C
A.2 B. C.0 D.0或2
【解析】 是关于 的一元一次不等式, 且 ,解得 .
【名师点睛】
一元一次不等式必须满足以下三个条件:(1)不等式的左右两边分母不含未知数;(2)不等式中只含一个未知数;(3)未知数的次数是1.三个条件缺一不可.
知识点4 利用一元一次不等式的性质解一元一次不等式
8.[2022株洲中考]不等式 的解集是( )
D
A. B. C. D.
【解析】 不等式两边都加1,得 ,两边都除以4,得 .
9.[2023张家口宣化区期末]不等式 的解集在
数轴上的表示如图所示,则阴影部分盖住的数是( )
C
A. B. C. D.
【解析】 不等式两边都减去 ,得 ,即 ,两边都除以 ,得 ,故阴影部分盖住的数是 .
10.解下列不等式,并把它们的解集在数轴上表示出来.
(1) ;
解: ,
不等式两边都减去 ,得 ,
两边都除以3,得 .
解集在数轴上表示,如图所示.
(2) .
解: ,
不等式两边都减去 ,得 ,
两边都除以 ,得 .
解集在数轴上表示,如图所示.
10.3 解一元一次不等式
课时1 一元一次不等式的有关概念及解法
过能力 学科关键能力构建
1.[2023保定期末]下面是两位同学在讨论一个一元一次不等式.
根据上面对话提供的信息,他们讨论的不等式是( )
C
A. B. C. D.
【解析】 由题图可知不等式的解集是 .A项,不等式 两边都除以2,得 ,不等式求解过程中没有变号,不符合题意;B项,不等式 ,两边都除以2,得 ,不符合题意;C项,不等式 ,两边都除以 ,得 ,不等式求解过程中有变号,符合题意;D项,不等式 ,两边都除以 ,得 ,不符合题意.
2.[2023保定定州北环路中学月考]若关于 的一元一次不等式 的解
都是 的解,则 的范围是( )
B
A. B. C. D.
【解析】 两边都减1,得 , 两边都除以2,得 不等式 的解都是 的解, .
变式 若 是不等式 的解, 不是不等式 的解,则下
列选项中,正确的是( )
B
A. B. C. D.
【解析】 两边都加上1,得 , 两边都除以2,得 是不等式 的解, 不是不等式 的解, , ,故 .
3. , 是常数,若 的解集是 ,则 的解集是
( )
D
A. B. C. D.
【解析】 由 的解集为 ,可知不等号方向改变,
且 , , , .由 得
, .
4.[2022随州曾都区一模]定义新运算“ ”,规定: .若关
于 的不等式 的解集为 ,则 的值是____.
【解析】 , , , 关于 的不等式 的解集为 , , .
5.[2021遂宁中考]已知关于 , 的二元一次方程组 满足
,则 的取值范围是_______.
【解析】 ,得 , , ,解得 .
6.教材P140T5变式[2022唐山二模]如图,在数轴上,点 , 分别表示数
2, .
(1)若 ,则点 , 间的距离是多少?
解:若 ,则 ,
此时点 , 分别表示数2,10, .
(2)若点 在点 的右边.
①求 的取值范围;
解: 点 在点 的右边, ,解得 .
②表示数 的点应落在___.(填序号)
B
A.点 左边 B.线段 上 C.点 右边
【解析】 , ,则 , 数轴上表示数 的点应落在点 的右边.又 , ,即数轴上表示数 的点在点 的左边, 数轴上表示 的点落在线段 上.
素养提升
7.推理能力[2022汉中期末]定义:如果一元一次不等式①的解都是一元一
次不等式②的解,那么称一元一次不等式①是一元一次不等式②的蕴含不
等式.例如:不等式 的解都是不等式 的解,则 是
的蕴含不等式.
(1)在不等式 , , 中,是 的蕴含不等式的是
_______;
(2)若 是 的蕴含不等式,求 的取值范围;
解:解不等式 ,可得 ,
因为 是 的蕴含不等式,
所以 ,解得 .
所以 的取值范围是 .
(3)若 是 的蕴含不等式,试判断 是不是
的蕴含不等式.
解:根据题意,得 ,
解得 ,所以 ,
所以 是 的蕴含不等式.
10.3 解一元一次不等式
课时1 一元一次不等式的有关概念及解法
过基础 教材必备知识精练
知识点1 不等式的解及解集的概念
1. 是下列哪个不等式的解( )
A
A. B. C. D.
【解析】 把 分别代入不等式中,能使不等式成立的就是不等式的解,只有A选项中不等式成立.
【策略点拨】
判断某个数是不是不等式的解
用这个数代替不等式中的未知数,看不等式是否成立,若成立,则该数是不等式的一个解;若不成立,则该数不是不等式的解.
2.有下列4个结论:① 是不等式 的解;② 是不等式
的解集;③ 是不等式 的解;④ 是不等式
的解集.其中正确结论的序号是( )
D
A.①② B.①②③ C.③④ D.①③④
【解析】 对于①, 能使不等式 成立,所以 是不等式 的解;对于②,不等式 的解集是 ,虽然 可以使不等式 成立,但不是这个不等式的解的全体,所以不是不等式 的解集;对于③, 能使不等式 成立,所以 是不等式 的解;对于④, 是不等式 的解集.
知识点2 不等式的解集的表示
3.[2023沈阳中考]不等式 的解集在数轴上表示正确的是( )
B
A.&4& B.&5& C.&6& D.&7&
【归纳总结】
在数轴上表示不等式的解集的步骤
画出数轴 找到对应点 判断实心或空心(带等号实心,不带等
号空心) 判断方向(大于向右画,小于向左画) 画出解集.
4.教材P125A组T2变式一个不等式的解集在数轴上的表示
如图所示,则这个不等式可能是( )
A
A. B. C. D.
【解析】 处是空心圆圈,且折线向右, 这个不等式的解集为 , 这个不等式可能是 .
5.在数轴上表示下列不等式的解集:
(1) ;
(2) .
知识点3 一元一次不等式的概念
6.[2022吉安期末]给出下列式子:① ;② ;③ ;
④ ;⑤ .其中是一元一次不等式的有( )
B
A.1个 B.2个 C.3个 D.4个
【解析】 , 是一元一次不等式,共2个.
7.易错题[2023保定十七中期中]若 是关于 的一元一
次不等式.则 的值为( )
C
A.2 B. C.0 D.0或2
【解析】 是关于 的一元一次不等式, 且 ,解得 .
【名师点睛】
一元一次不等式必须满足以下三个条件:(1)不等式的左右两边分母不含未知数;(2)不等式中只含一个未知数;(3)未知数的次数是1.三个条件缺一不可.
知识点4 利用一元一次不等式的性质解一元一次不等式
8.[2022株洲中考]不等式 的解集是( )
D
A. B. C. D.
【解析】 不等式两边都加1,得 ,两边都除以4,得 .
9.[2023张家口宣化区期末]不等式 的解集在
数轴上的表示如图所示,则阴影部分盖住的数是( )
C
A. B. C. D.
【解析】 不等式两边都减去 ,得 ,即 ,两边都除以 ,得 ,故阴影部分盖住的数是 .
10.解下列不等式,并把它们的解集在数轴上表示出来.
(1) ;
解: ,
不等式两边都减去 ,得 ,
两边都除以3,得 .
解集在数轴上表示,如图所示.
(2) .
解: ,
不等式两边都减去 ,得 ,
两边都除以 ,得 .
解集在数轴上表示,如图所示.
10.3 解一元一次不等式
课时1 一元一次不等式的有关概念及解法
过能力 学科关键能力构建
1.[2023保定期末]下面是两位同学在讨论一个一元一次不等式.
根据上面对话提供的信息,他们讨论的不等式是( )
C
A. B. C. D.
【解析】 由题图可知不等式的解集是 .A项,不等式 两边都除以2,得 ,不等式求解过程中没有变号,不符合题意;B项,不等式 ,两边都除以2,得 ,不符合题意;C项,不等式 ,两边都除以 ,得 ,不等式求解过程中有变号,符合题意;D项,不等式 ,两边都除以 ,得 ,不符合题意.
2.[2023保定定州北环路中学月考]若关于 的一元一次不等式 的解
都是 的解,则 的范围是( )
B
A. B. C. D.
【解析】 两边都减1,得 , 两边都除以2,得 不等式 的解都是 的解, .
变式 若 是不等式 的解, 不是不等式 的解,则下
列选项中,正确的是( )
B
A. B. C. D.
【解析】 两边都加上1,得 , 两边都除以2,得 是不等式 的解, 不是不等式 的解, , ,故 .
3. , 是常数,若 的解集是 ,则 的解集是
( )
D
A. B. C. D.
【解析】 由 的解集为 ,可知不等号方向改变,
且 , , , .由 得
, .
4.[2022随州曾都区一模]定义新运算“ ”,规定: .若关
于 的不等式 的解集为 ,则 的值是____.
【解析】 , , , 关于 的不等式 的解集为 , , .
5.[2021遂宁中考]已知关于 , 的二元一次方程组 满足
,则 的取值范围是_______.
【解析】 ,得 , , ,解得 .
6.教材P140T5变式[2022唐山二模]如图,在数轴上,点 , 分别表示数
2, .
(1)若 ,则点 , 间的距离是多少?
解:若 ,则 ,
此时点 , 分别表示数2,10, .
(2)若点 在点 的右边.
①求 的取值范围;
解: 点 在点 的右边, ,解得 .
②表示数 的点应落在___.(填序号)
B
A.点 左边 B.线段 上 C.点 右边
【解析】 , ,则 , 数轴上表示数 的点应落在点 的右边.又 , ,即数轴上表示数 的点在点 的左边, 数轴上表示 的点落在线段 上.
素养提升
7.推理能力[2022汉中期末]定义:如果一元一次不等式①的解都是一元一
次不等式②的解,那么称一元一次不等式①是一元一次不等式②的蕴含不
等式.例如:不等式 的解都是不等式 的解,则 是
的蕴含不等式.
(1)在不等式 , , 中,是 的蕴含不等式的是
_______;
(2)若 是 的蕴含不等式,求 的取值范围;
解:解不等式 ,可得 ,
因为 是 的蕴含不等式,
所以 ,解得 .
所以 的取值范围是 .
(3)若 是 的蕴含不等式,试判断 是不是
的蕴含不等式.
解:根据题意,得 ,
解得 ,所以 ,
所以 是 的蕴含不等式.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
