第七章 相交线与平行线专项1 习题课件(共46张PPT)2023-2024学年冀教版数学七年级下册
文档属性
| 名称 | 第七章 相交线与平行线专项1 习题课件(共46张PPT)2023-2024学年冀教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 00:00:00 | ||
图片预览

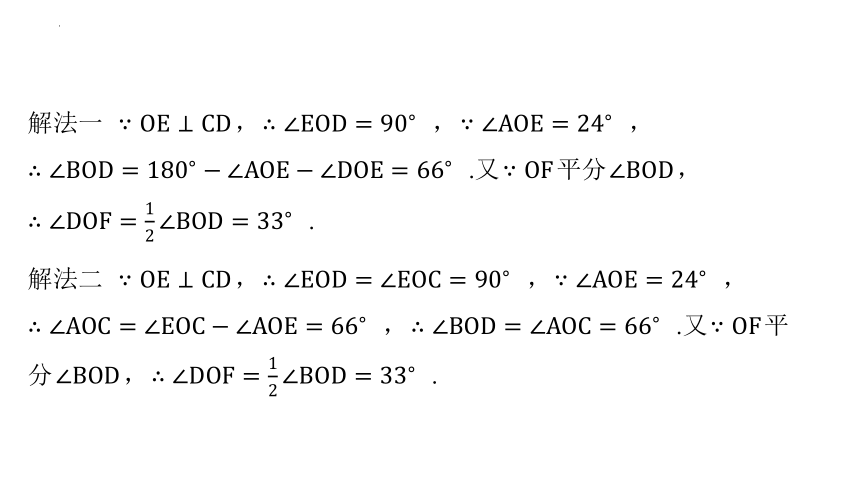








文档简介
(共46张PPT)
第七章 相交线与平行线
专项1 与垂直、平行线有关的角的计算
过专项 阶段强化专项训练
类型1 与垂直有关的计算
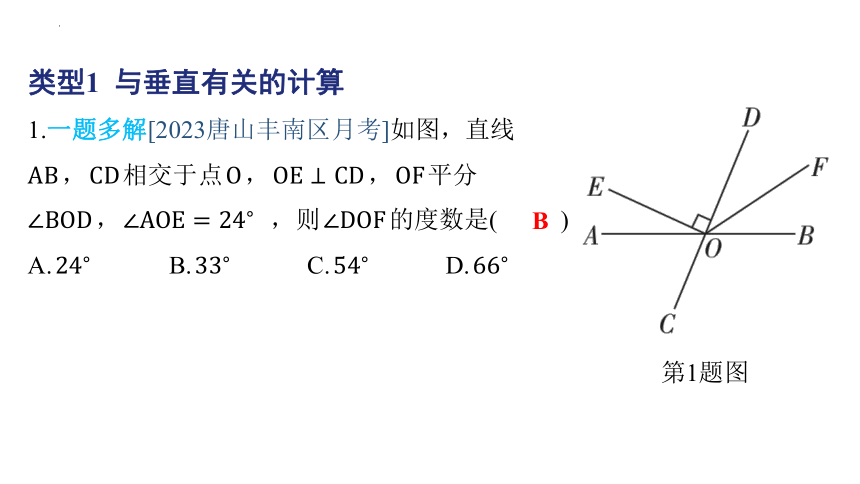
第1题图
1.一题多解[2023唐山丰南区月考]如图,直线
, 相交于点 , , 平分
, ,则 的度数是( )
B
A. B. C. D.
解法一 , , ,
.又 平分 ,
.
解法二 , , ,
, .又 平
分 , .
第2题图
2.如图,直线 和 相交于点 , ,若
,则 的度数为______ .
157.5
【解析】 , , , , .
类型2 与平行线有关的计算
第3题图
3.一题多解[2022长沙中考]如图,
, , ,则
的度数为( )
C
A. B. C. D.
解法一 如图,因为 ,所以 .因为 ,
所以 .
解法二如图,因为 ,所以 .因为 ,
所以 .
第4题图
4.[2023石家庄四中期中]如图,把一张对边互
相平行的纸条沿 折叠,若 ,
给出下列结论:① ;②
;③ ;④
.其中正确的有( )
B
A.4个 B.3个 C.2个 D.1个
【解析】 根据题意,得 , ,故①正
确; 是折痕, ,则
, ,
,故②正确;
, ,故③正确; ,
, , ,
,故④错误.
【归纳总结】
有关折叠问题中的对应关系
图形折叠问题中,折叠前后的两个图形是完全相同的,据此可以得到对应图形的对应角相等,对应线段相等,这是解决折叠问题的关键.
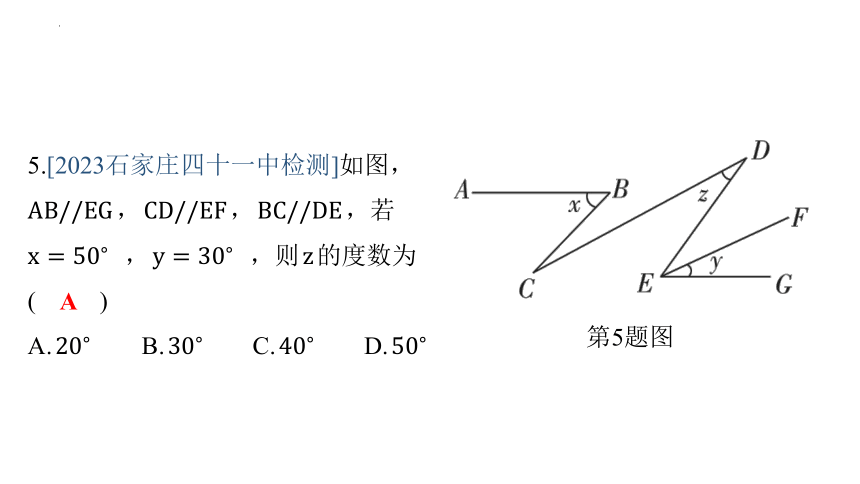
第5题图
5.[2023石家庄四十一中检测]如图,
, , ,若
, ,则 的度数为
( )
A
A. B. C. D.
【解析】 如图,延长 交 于点 , ,
, , ,
.又 , ,
.
第6题图
6.[2022台州书生中学开学考试]如图, ,
, , ,则 的度数是
_____.
【解析】 , , ,又 , , , , .
类型3 与垂直、平行线有关的角的计算
7.[2023泰安中考]把一块直角三角板和一把直尺如图
放置,若 ,则 的度数等于( )
B
A. B. C. D.
【解析】 如图,过点 作 , ,
, ,
,
, , .
8.[2022南京模拟]如图,已知 ,
.
(1)请说明 的理由.
解:因为 ,
所以 ,所以 .
因为 ,所以 ,
所以 .
(2)若 平分 , 于点 , ,求 的度数.
解:因为 , ,
所以 .
因为 平分 ,所以 .
因为 ,所以 .
因为 ,所以 ,
又因为 ,所以 ,
所以 .
专项2 平行线中的“拐点”问题
过专项 阶段强化专项训练
类型1 单“拐点”模型
模型总结
第1题图
1.[2023鄂州中考]如图,直线 ,
于点 .若 ,则
的度数是( )
B
A. B. C. D.
【解析】 过点 作直线 (平行线之间有“拐点”
的问题,通常是过“拐点”作已知直线的平行线),如
图. , ,
,
, .
第2题图
2.[2023黄山期末]如图,已知 , ,
,则 的度数是( )
C
A. B. C. D.
【解析】 如图,过点 作 .因为 ,所
以 .因为 , ,所
以 , ,所以
.
3.[2023连云港赣县榆实验中学期中]为增强学生体质,弘扬中国传统文化,
学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,小聪把它抽
象成图2的数学问题:已知 , , ,则
的度数是( )
图1
图2
A. B. C. D.
√
A
【解析】 如图,过点 作 ,
,
,
, ,
, ,
.
变式 [2023唐山丰南区期中]某兴趣
小组利用几何图形画出螳螂的简笔
画,如图,已知 ,
20
, ,则 ____ .
【解析】 过点 作 ,如图,
, ,
, .
又 , ,
, , .
4.已知平面内的直线有相交和平行两种位置关系.
(1)如图1,已知 ,试说明: .
图1
图1
解:过点 作 ,如图1所示.
因为 ,(辅助线)
,(已知)
所以 ,(在同一平面内,平行于同
一直线的两条直线平行)
所以 , ,(两直线平行,内错角相等)
所以 .(等量代换)
(2)如图2,已知 ,试说明: .
图2
图2
解:过点 作 ,如图2所示.
因为 ,(辅助线)
所以 ,(两直线平行,同位
角相等)
,(两直线平行,内错角相等)
所以 .(等量代换)
(3)根据图3,试判断 , , , 之间的数量关系,并说
明理由.
图3
图3
解:数量关系: .理由如下:
过点 作 ,过点 作 ,如图3所
示.
则 ,
所以 , ,(两直线
平行,同旁内角互补)
.(两直线平行,内错角相等)
又因为 ,
所以 ,
所以 ,
所以 .(等量代换)
类型2 多“拐点”模型
模型总结
5.[2022武汉新洲区期末]如图, ,则 , , ,
满足的数量关系是( )
A
A. B.
C. D.
【解析】 如图,过点 作 ,过点 作 ,
则 , ,
, ,
,
.
6.如图,若 ,则图中 的度数是____ .
72
【解析】 如图,过两平行线中间角的顶点作 的平行
线, ,由平行线的性质可得
,解得 .
7.[2022烟台牟平区期中]越野滑雪是
冬奥会的一个重要比赛项目,是借
助滑雪用具,运用登山,滑降,转
弯滑行等基本技术,滑行于雪山、雪原的运动项目.为了保证运动员的安
全,在修建赛道时要避开冰带,陡角和狭窄地带.如图,在修建赛道时为了
避开冰带需拐弯绕之,若第一次拐的 ,第二次拐的
,第三次拐的是 ,这时道路恰好和第一次拐弯之前的道路
平行,则 ______.
【解析】 过点 作 ,如图. ,
, ,
,
, ,
.
8.如图,点 , 分别在直线 , 上, .
(1)如图1,连接 ,则 _____ .
180
图1
图2
(2)如图2,点 是直线 , 内部的一个点,连接
, .试说明: .
图1
解:如图1,过点 作 ,易知
,
,
,
.
图3
(3)如图3,点 , 是直线 , 内部两个不重合的
点,连接 , , .试求
的度数.
图2
解:如图2,过点 作 ,过点
作 ,易知 ,
,
,
,
.
(4)若按以上规律,猜想并直接写出 的
度数(不必写出过程).
解: .
第七章 相交线与平行线
专项1 与垂直、平行线有关的角的计算
过专项 阶段强化专项训练
类型1 与垂直有关的计算
第1题图
1.一题多解[2023唐山丰南区月考]如图,直线
, 相交于点 , , 平分
, ,则 的度数是( )
B
A. B. C. D.
解法一 , , ,
.又 平分 ,
.
解法二 , , ,
, .又 平
分 , .
第2题图
2.如图,直线 和 相交于点 , ,若
,则 的度数为______ .
157.5
【解析】 , , , , .
类型2 与平行线有关的计算
第3题图
3.一题多解[2022长沙中考]如图,
, , ,则
的度数为( )
C
A. B. C. D.
解法一 如图,因为 ,所以 .因为 ,
所以 .
解法二如图,因为 ,所以 .因为 ,
所以 .
第4题图
4.[2023石家庄四中期中]如图,把一张对边互
相平行的纸条沿 折叠,若 ,
给出下列结论:① ;②
;③ ;④
.其中正确的有( )
B
A.4个 B.3个 C.2个 D.1个
【解析】 根据题意,得 , ,故①正
确; 是折痕, ,则
, ,
,故②正确;
, ,故③正确; ,
, , ,
,故④错误.
【归纳总结】
有关折叠问题中的对应关系
图形折叠问题中,折叠前后的两个图形是完全相同的,据此可以得到对应图形的对应角相等,对应线段相等,这是解决折叠问题的关键.
第5题图
5.[2023石家庄四十一中检测]如图,
, , ,若
, ,则 的度数为
( )
A
A. B. C. D.
【解析】 如图,延长 交 于点 , ,
, , ,
.又 , ,
.
第6题图
6.[2022台州书生中学开学考试]如图, ,
, , ,则 的度数是
_____.
【解析】 , , ,又 , , , , .
类型3 与垂直、平行线有关的角的计算
7.[2023泰安中考]把一块直角三角板和一把直尺如图
放置,若 ,则 的度数等于( )
B
A. B. C. D.
【解析】 如图,过点 作 , ,
, ,
,
, , .
8.[2022南京模拟]如图,已知 ,
.
(1)请说明 的理由.
解:因为 ,
所以 ,所以 .
因为 ,所以 ,
所以 .
(2)若 平分 , 于点 , ,求 的度数.
解:因为 , ,
所以 .
因为 平分 ,所以 .
因为 ,所以 .
因为 ,所以 ,
又因为 ,所以 ,
所以 .
专项2 平行线中的“拐点”问题
过专项 阶段强化专项训练
类型1 单“拐点”模型
模型总结
第1题图
1.[2023鄂州中考]如图,直线 ,
于点 .若 ,则
的度数是( )
B
A. B. C. D.
【解析】 过点 作直线 (平行线之间有“拐点”
的问题,通常是过“拐点”作已知直线的平行线),如
图. , ,
,
, .
第2题图
2.[2023黄山期末]如图,已知 , ,
,则 的度数是( )
C
A. B. C. D.
【解析】 如图,过点 作 .因为 ,所
以 .因为 , ,所
以 , ,所以
.
3.[2023连云港赣县榆实验中学期中]为增强学生体质,弘扬中国传统文化,
学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,小聪把它抽
象成图2的数学问题:已知 , , ,则
的度数是( )
图1
图2
A. B. C. D.
√
A
【解析】 如图,过点 作 ,
,
,
, ,
, ,
.
变式 [2023唐山丰南区期中]某兴趣
小组利用几何图形画出螳螂的简笔
画,如图,已知 ,
20
, ,则 ____ .
【解析】 过点 作 ,如图,
, ,
, .
又 , ,
, , .
4.已知平面内的直线有相交和平行两种位置关系.
(1)如图1,已知 ,试说明: .
图1
图1
解:过点 作 ,如图1所示.
因为 ,(辅助线)
,(已知)
所以 ,(在同一平面内,平行于同
一直线的两条直线平行)
所以 , ,(两直线平行,内错角相等)
所以 .(等量代换)
(2)如图2,已知 ,试说明: .
图2
图2
解:过点 作 ,如图2所示.
因为 ,(辅助线)
所以 ,(两直线平行,同位
角相等)
,(两直线平行,内错角相等)
所以 .(等量代换)
(3)根据图3,试判断 , , , 之间的数量关系,并说
明理由.
图3
图3
解:数量关系: .理由如下:
过点 作 ,过点 作 ,如图3所
示.
则 ,
所以 , ,(两直线
平行,同旁内角互补)
.(两直线平行,内错角相等)
又因为 ,
所以 ,
所以 ,
所以 .(等量代换)
类型2 多“拐点”模型
模型总结
5.[2022武汉新洲区期末]如图, ,则 , , ,
满足的数量关系是( )
A
A. B.
C. D.
【解析】 如图,过点 作 ,过点 作 ,
则 , ,
, ,
,
.
6.如图,若 ,则图中 的度数是____ .
72
【解析】 如图,过两平行线中间角的顶点作 的平行
线, ,由平行线的性质可得
,解得 .
7.[2022烟台牟平区期中]越野滑雪是
冬奥会的一个重要比赛项目,是借
助滑雪用具,运用登山,滑降,转
弯滑行等基本技术,滑行于雪山、雪原的运动项目.为了保证运动员的安
全,在修建赛道时要避开冰带,陡角和狭窄地带.如图,在修建赛道时为了
避开冰带需拐弯绕之,若第一次拐的 ,第二次拐的
,第三次拐的是 ,这时道路恰好和第一次拐弯之前的道路
平行,则 ______.
【解析】 过点 作 ,如图. ,
, ,
,
, ,
.
8.如图,点 , 分别在直线 , 上, .
(1)如图1,连接 ,则 _____ .
180
图1
图2
(2)如图2,点 是直线 , 内部的一个点,连接
, .试说明: .
图1
解:如图1,过点 作 ,易知
,
,
,
.
图3
(3)如图3,点 , 是直线 , 内部两个不重合的
点,连接 , , .试求
的度数.
图2
解:如图2,过点 作 ,过点
作 ,易知 ,
,
,
,
.
(4)若按以上规律,猜想并直接写出 的
度数(不必写出过程).
解: .
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
