21.4.1 单个一次函数的应用 习题课件(基础+能力共32张PPT)2023-2024学年冀教版数学八年级下册
文档属性
| 名称 | 21.4.1 单个一次函数的应用 习题课件(基础+能力共32张PPT)2023-2024学年冀教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 08:10:33 | ||
图片预览











文档简介
(共32张PPT)
21.4 一次函数的应用
课时1 单个一次函数的应用
过基础 教材必备知识精练
1.[2023宝鸡陈仓区三模]某品牌鞋子的长度 与鞋子的码数 之间满
足一次函数关系.若22码鞋子的长度为 ,44码鞋子的长度为 ,
则38码鞋子的长度为( )
B
A. B. C. D.
【解析】 设 与 之间的函数关系式为 ,将
, 分别代入,得 解得 所以
,所以当 时, ,所以38
码鞋子的长度为 .
第2题图
2.某长途汽车客运公司规定旅客可免费携带一定质量
的行李,当行李的质量超过规定时,需付的行李费
(元)是行李质量 的一次函数,其图像如图所
示.则旅客最多可免费携带行李的质量为( )
B
A. B. C. D.
【解析】 设 与 的函数表达式为 ,将 ,
代入,得 解得 ,令 ,
即 ,解得 .
第3题图
3.新趋势·传统文化 教材P100T1变式[2023镇江八校联考]漏刻
是我国古代的一种计时工具.据史书记载,西周时期就已经出
现了漏刻,这是中国古代人民对函数思想的创造性应用.小明
同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,
研究中发现水位 是时间 的一次函数,如表是小
… 1 2 3 5 …
… 2.4 2.8 3.4 4 …
明记录的部分数据,其中有一个 的值记录错误,请排除后利用正确的数
据确定当 为8时,对应的时间 为_ _________.
【解析】 设一次函数的表达式为 , 每增加一个单位, 的值
增加 个单位,所以由题表可知,当 时, 的值记录错误.将
, 代入 ,得 解得 所以
,当 时, .
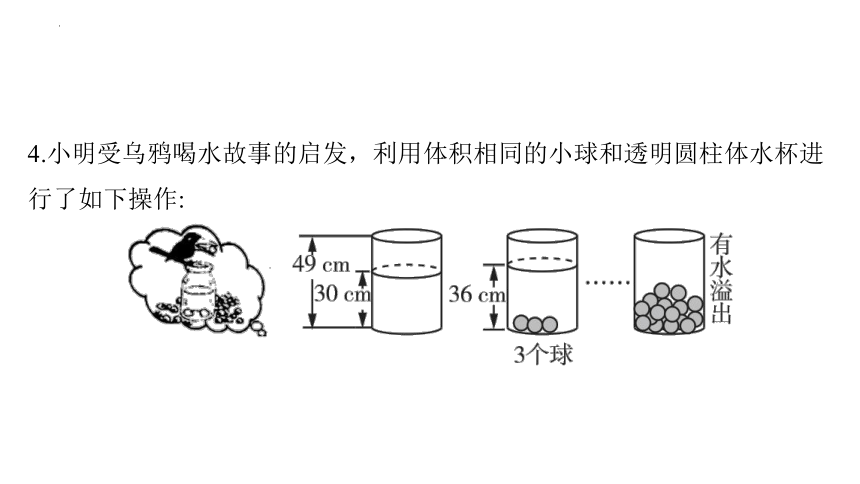
4.小明受乌鸦喝水故事的启发,利用体积相同的小球和透明圆柱体水杯进行了如下操作:
请根据图中给出的信息,解答下列问题:
(1)若放入一个小球,则水杯中水面升高___ .
2
【解析】 由题图知,放入3个小球,水杯中水面高度从 升高到 ,故放入1个小球,水杯中水面升高 .
(2)求放入小球后水杯中水面的高度 与小球个数 (个)之间的
一次函数关系式.(不要求写出自变量 的取值范围)
解:设水杯中水面的高度 与小球个数 之间的一次函数关系式为
,
将 , 分别代入,
得 解得
所以所求一次函数关系式为 .
(3)水杯中至少放入几个小球时有水溢出
解:由题意得, ,所以 ,
即水杯中至少放入10个小球时有水溢出.
5.[2023渭南期末]常温下,有一种烧水壶加热1.5升的纯净水时,加热中的水温 与加热时间 (秒)之间近似满足一次函数关系.经试验可知,在常温下,用这种壶将1.5升的纯净水加热到 时,所用时间为3分16秒,再加热40秒,水温正好达到 .
(1)求出 与 之间的函数关系式.
解:3分16秒 秒, (秒)(注意:单位要统一),
设 与 之间的函数关系式是 ,
根据题意可知,当 时, ;当 时, ,
则 解得
与 之间的函数关系式为 .
(2)在常温下,若用这种烧水壶将1.5升的 纯净水烧开(温度为
),则需加热多长时间?
解:在 中,令 ,则 ,
解得 ,
令 ,则 ,解得 ,
则 (秒).
故用这种烧水壶将1.5升的 纯净水烧开,需加热的时间为288秒.
21.4 一次函数的应用
课时1 单个一次函数的应用
过能力 学科关键能力构建
1.如图1是我国青海湖最深处的某一截面图,青
海湖水面下任意一点 处的压强 (单位:
)与其离水面的深度 (单位: )的函
数表达式为 ,其图像如图2所示,
A
A.青海湖水深 处的压强约为
B.青海湖水面大气压强为
C.函数表达式 中自变量 的取值范围是
D. 与 的函数表达式为
其中 为青海湖水面大气压强, 为常数且 .根据图中信息分析
( 的值和结果保留一位小数),下列结论正确的是( )
【解析】 由题中图像可知,直线 过点 和
, 解得 直线表达式为
,故D错误;青海湖水面大气压强为 ,故B错误;
根据函数表达式 的实际意义,得自变量 的取值范围是
,故C错误;将 代入表达式 ,可得
,即青海湖水深 处的压强约为
,故A正确.
2.[2023吉林中考]甲、乙两个工程组同时挖掘沈白高铁
某段隧道,两组每天挖掘长度均保持不变,合作一段
时间后,乙组因维修设备而停工,甲组单独完成了剩
下的任务,甲、乙两组挖掘的长度之和 与甲组挖
掘时间 (天)之间的关系如图所示.
(1)甲组比乙组多挖掘了____天.
30
【解析】 由题图可知,前30天甲、乙两组合作,30天以后甲组单独做,所以甲组挖掘了60天,乙组挖掘了30天,所以甲组比乙组多挖掘的时间为 (天).
(2)求乙组停工后 关于 的函数表达式,并写出自变量 的取值范围.
解:设乙组停工后 关于 的函数表达式为 ,
将 和 代入,可得
解得
所以 .
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
解:乙组已停工的天数为10天.
甲组每天挖掘的长度为 ,
甲、乙合作每天挖掘的长度为 ,
所以乙组每天挖掘的长度为 ,
则乙组挖掘的总长度为 .
设乙组已停工的天数为 天,
则 ,解得 ,
故乙组已停工的天数为10天.
【策略点拨】
解决图像类应用题的策略
(1)看轴:明确横轴和纵轴表示的量.
(2)看点:明确各关键点表示的实际意义.
(3)看线:明确每一段图像下对应的自变量的取值范围及图像类型.
3.新趋势·传统文化[2023陕西师大附中模拟]我国传统的计重工具——秤,它的应用方便了人们的生活,如图1,可以用秤砣到秤纽的水平距离来得出秤钩上所挂物体的质量.称重时,若秤杆上秤砣到秤纽的水平距离为 (厘米),秤钩上所挂物体的质量为 (斤).若干次称重时所记录的一些数据如表所示.
厘米 1 2 4 8
斤 0.75 1.00 1.50 2.50
(1)在图2中描出表中的数据,观察判断 , 的函数关系,并求秤杆上
秤砣到秤纽的水平距离为16厘米时,秤钩上所挂物体的质量.
解:描点如图所示,这些点在一条直线上,故 与
满足一次函数关系.
设 关于 的函数关系式为 ,
因为当 时, ,当 时, ,
所以 解得
所以 .
验证:当 时, ,
当 时, ,
所以 关于 的函数关系式为 .
把 代入 ,得 .
所以秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩上所挂物体的质量是
4.5斤.
(2)已知秤砣到秤纽的最大水平距离为50厘米,这杆秤的可称物重范围是多少?
解:把 代入 ,得 ,
所以 ,
所以这杆秤的可称物重范围是大于0斤小于等于13斤.
4.某农业合作社计划投资200万元,开展甲、乙两个种植项目.已知两个项
目的收益(万元)均与投资金额(万元)成正比例,但比例系数不同,设
投资甲项目的资金为 万元,两个项目的总收益为 万元,且在经营过程
中,得到部分数据如下表:
万元 10 120
万元 79 68
(1)求 与 之间的函数关系式(不要求写出自变量 的取值范围).
解:由题意知,投资甲项目的资金为 万元,
则投资乙项目的资金为 万元,
设甲、乙两个项目收益的比例系数分别为 , ,则 ,
由题表可得,
解得
所以 .
(2)嘉淇说:“两个项目的总收益可以是50万元.”你同意他的说法吗 说明你的理由.
解:不同意.理由如下:
由题意得, ,解得 ,
由于 ,故 不符合题意,
即两个项目的总收益不可能是50万元.
(3)若甲项目的收益不低于乙项目的收益的 ,求 的最大值.
解:由题意得, ,
解得 ,
由于 ,因此 随 的增大而减小,
所以当 时, 取得最大值,最大值为
(万元).
21.4 一次函数的应用
课时1 单个一次函数的应用
过基础 教材必备知识精练
1.[2023宝鸡陈仓区三模]某品牌鞋子的长度 与鞋子的码数 之间满
足一次函数关系.若22码鞋子的长度为 ,44码鞋子的长度为 ,
则38码鞋子的长度为( )
B
A. B. C. D.
【解析】 设 与 之间的函数关系式为 ,将
, 分别代入,得 解得 所以
,所以当 时, ,所以38
码鞋子的长度为 .
第2题图
2.某长途汽车客运公司规定旅客可免费携带一定质量
的行李,当行李的质量超过规定时,需付的行李费
(元)是行李质量 的一次函数,其图像如图所
示.则旅客最多可免费携带行李的质量为( )
B
A. B. C. D.
【解析】 设 与 的函数表达式为 ,将 ,
代入,得 解得 ,令 ,
即 ,解得 .
第3题图
3.新趋势·传统文化 教材P100T1变式[2023镇江八校联考]漏刻
是我国古代的一种计时工具.据史书记载,西周时期就已经出
现了漏刻,这是中国古代人民对函数思想的创造性应用.小明
同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,
研究中发现水位 是时间 的一次函数,如表是小
… 1 2 3 5 …
… 2.4 2.8 3.4 4 …
明记录的部分数据,其中有一个 的值记录错误,请排除后利用正确的数
据确定当 为8时,对应的时间 为_ _________.
【解析】 设一次函数的表达式为 , 每增加一个单位, 的值
增加 个单位,所以由题表可知,当 时, 的值记录错误.将
, 代入 ,得 解得 所以
,当 时, .
4.小明受乌鸦喝水故事的启发,利用体积相同的小球和透明圆柱体水杯进行了如下操作:
请根据图中给出的信息,解答下列问题:
(1)若放入一个小球,则水杯中水面升高___ .
2
【解析】 由题图知,放入3个小球,水杯中水面高度从 升高到 ,故放入1个小球,水杯中水面升高 .
(2)求放入小球后水杯中水面的高度 与小球个数 (个)之间的
一次函数关系式.(不要求写出自变量 的取值范围)
解:设水杯中水面的高度 与小球个数 之间的一次函数关系式为
,
将 , 分别代入,
得 解得
所以所求一次函数关系式为 .
(3)水杯中至少放入几个小球时有水溢出
解:由题意得, ,所以 ,
即水杯中至少放入10个小球时有水溢出.
5.[2023渭南期末]常温下,有一种烧水壶加热1.5升的纯净水时,加热中的水温 与加热时间 (秒)之间近似满足一次函数关系.经试验可知,在常温下,用这种壶将1.5升的纯净水加热到 时,所用时间为3分16秒,再加热40秒,水温正好达到 .
(1)求出 与 之间的函数关系式.
解:3分16秒 秒, (秒)(注意:单位要统一),
设 与 之间的函数关系式是 ,
根据题意可知,当 时, ;当 时, ,
则 解得
与 之间的函数关系式为 .
(2)在常温下,若用这种烧水壶将1.5升的 纯净水烧开(温度为
),则需加热多长时间?
解:在 中,令 ,则 ,
解得 ,
令 ,则 ,解得 ,
则 (秒).
故用这种烧水壶将1.5升的 纯净水烧开,需加热的时间为288秒.
21.4 一次函数的应用
课时1 单个一次函数的应用
过能力 学科关键能力构建
1.如图1是我国青海湖最深处的某一截面图,青
海湖水面下任意一点 处的压强 (单位:
)与其离水面的深度 (单位: )的函
数表达式为 ,其图像如图2所示,
A
A.青海湖水深 处的压强约为
B.青海湖水面大气压强为
C.函数表达式 中自变量 的取值范围是
D. 与 的函数表达式为
其中 为青海湖水面大气压强, 为常数且 .根据图中信息分析
( 的值和结果保留一位小数),下列结论正确的是( )
【解析】 由题中图像可知,直线 过点 和
, 解得 直线表达式为
,故D错误;青海湖水面大气压强为 ,故B错误;
根据函数表达式 的实际意义,得自变量 的取值范围是
,故C错误;将 代入表达式 ,可得
,即青海湖水深 处的压强约为
,故A正确.
2.[2023吉林中考]甲、乙两个工程组同时挖掘沈白高铁
某段隧道,两组每天挖掘长度均保持不变,合作一段
时间后,乙组因维修设备而停工,甲组单独完成了剩
下的任务,甲、乙两组挖掘的长度之和 与甲组挖
掘时间 (天)之间的关系如图所示.
(1)甲组比乙组多挖掘了____天.
30
【解析】 由题图可知,前30天甲、乙两组合作,30天以后甲组单独做,所以甲组挖掘了60天,乙组挖掘了30天,所以甲组比乙组多挖掘的时间为 (天).
(2)求乙组停工后 关于 的函数表达式,并写出自变量 的取值范围.
解:设乙组停工后 关于 的函数表达式为 ,
将 和 代入,可得
解得
所以 .
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
解:乙组已停工的天数为10天.
甲组每天挖掘的长度为 ,
甲、乙合作每天挖掘的长度为 ,
所以乙组每天挖掘的长度为 ,
则乙组挖掘的总长度为 .
设乙组已停工的天数为 天,
则 ,解得 ,
故乙组已停工的天数为10天.
【策略点拨】
解决图像类应用题的策略
(1)看轴:明确横轴和纵轴表示的量.
(2)看点:明确各关键点表示的实际意义.
(3)看线:明确每一段图像下对应的自变量的取值范围及图像类型.
3.新趋势·传统文化[2023陕西师大附中模拟]我国传统的计重工具——秤,它的应用方便了人们的生活,如图1,可以用秤砣到秤纽的水平距离来得出秤钩上所挂物体的质量.称重时,若秤杆上秤砣到秤纽的水平距离为 (厘米),秤钩上所挂物体的质量为 (斤).若干次称重时所记录的一些数据如表所示.
厘米 1 2 4 8
斤 0.75 1.00 1.50 2.50
(1)在图2中描出表中的数据,观察判断 , 的函数关系,并求秤杆上
秤砣到秤纽的水平距离为16厘米时,秤钩上所挂物体的质量.
解:描点如图所示,这些点在一条直线上,故 与
满足一次函数关系.
设 关于 的函数关系式为 ,
因为当 时, ,当 时, ,
所以 解得
所以 .
验证:当 时, ,
当 时, ,
所以 关于 的函数关系式为 .
把 代入 ,得 .
所以秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩上所挂物体的质量是
4.5斤.
(2)已知秤砣到秤纽的最大水平距离为50厘米,这杆秤的可称物重范围是多少?
解:把 代入 ,得 ,
所以 ,
所以这杆秤的可称物重范围是大于0斤小于等于13斤.
4.某农业合作社计划投资200万元,开展甲、乙两个种植项目.已知两个项
目的收益(万元)均与投资金额(万元)成正比例,但比例系数不同,设
投资甲项目的资金为 万元,两个项目的总收益为 万元,且在经营过程
中,得到部分数据如下表:
万元 10 120
万元 79 68
(1)求 与 之间的函数关系式(不要求写出自变量 的取值范围).
解:由题意知,投资甲项目的资金为 万元,
则投资乙项目的资金为 万元,
设甲、乙两个项目收益的比例系数分别为 , ,则 ,
由题表可得,
解得
所以 .
(2)嘉淇说:“两个项目的总收益可以是50万元.”你同意他的说法吗 说明你的理由.
解:不同意.理由如下:
由题意得, ,解得 ,
由于 ,故 不符合题意,
即两个项目的总收益不可能是50万元.
(3)若甲项目的收益不低于乙项目的收益的 ,求 的最大值.
解:由题意得, ,
解得 ,
由于 ,因此 随 的增大而减小,
所以当 时, 取得最大值,最大值为
(万元).
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
