20.1.1平均数(第1课时)教学设计-2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 20.1.1平均数(第1课时)教学设计-2023—2024学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 14:18:28 | ||
图片预览

文档简介
20.1.1平均数(第1课时)教学设计
教材分析:
根据《课标(2022年版)》的要求,在第二学段已经学习了有关平均数的知识.本节在复习相关内容的基础上,继续学习加权平均数、中位数和众数,并用样本的(加权)平均数、中位数、众数估计总体相应的数字特征等内容.第20.1.1小节研究加权平均数,包括权的意义、作用和不同的形式.首先,教科书设计了以招聘英文翻译为背景的实际问题,根据不同的招聘要求,各项成绩的“重要程度”不同,从而平均成绩不同,由此引入加权平均数的概念.权的重要性在于它能够反映数据的相对“重要程度”.为了更好的说明这一点,教科书设置“思考”栏目和例1,从不同方面体现权的作用,使学生更好的理解加权平均数,体会权的意义和作用.求加权平均数的问题形式多样,教科书在问题1和例1之后又介绍了两种:一是在求n个数的算术平均数时,有时会遇到重复数据较多的情况,这时可以将求算术平均数的公式进行简化,只是这里权的意义并不是很突出;二是通过一个“探究”栏目研究了对于区间分组的数据如何求加权平均数的问题,这类问题是统计中常见的.通过不同形式的问题,教科书希望学生能对加权平均数有一个全面的认识.最后教科书结合例3,介绍了如何利用样本平均数估计总体平均数的问题,使学生对抽样的必要性、样本的代表性和用样本估计总体的思想有了更深的体会.
综上所述,本节可以分为3个课时.第1课时的教学重点放在对权及加权平均数统计意义的理解.理解平均数如何刻画数据的集中趋势.分析数据时,这些统计量需要通过计算来得到,有些计算会比较复杂.统计量的复杂计算不应作为该部分教学的重点,教学中不应过分强调计算.教师应引导学生使用计算器、计算机等进行数据计算,可以与信息科技课程学习结合,开展跨学科主题学习活动,鼓励学生设计算法、编写程序来计算统计量.由于学生身处偏远农村地区,学生计算机的应用水平有限,所以统计量的计算,在课上主要是分组完成.
教学目标:
1、理解数据的权和加权平均数的统计意义.
2、掌握加权平均数的计算方法,会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析的观念.
学习重点:
对权及加权平均数统计意义的理解,会计算加权平均数.
学习难点:对权的意义理解,用加权平均数描述数据的集中趋势.
教学过程设计:
一、身边的数学
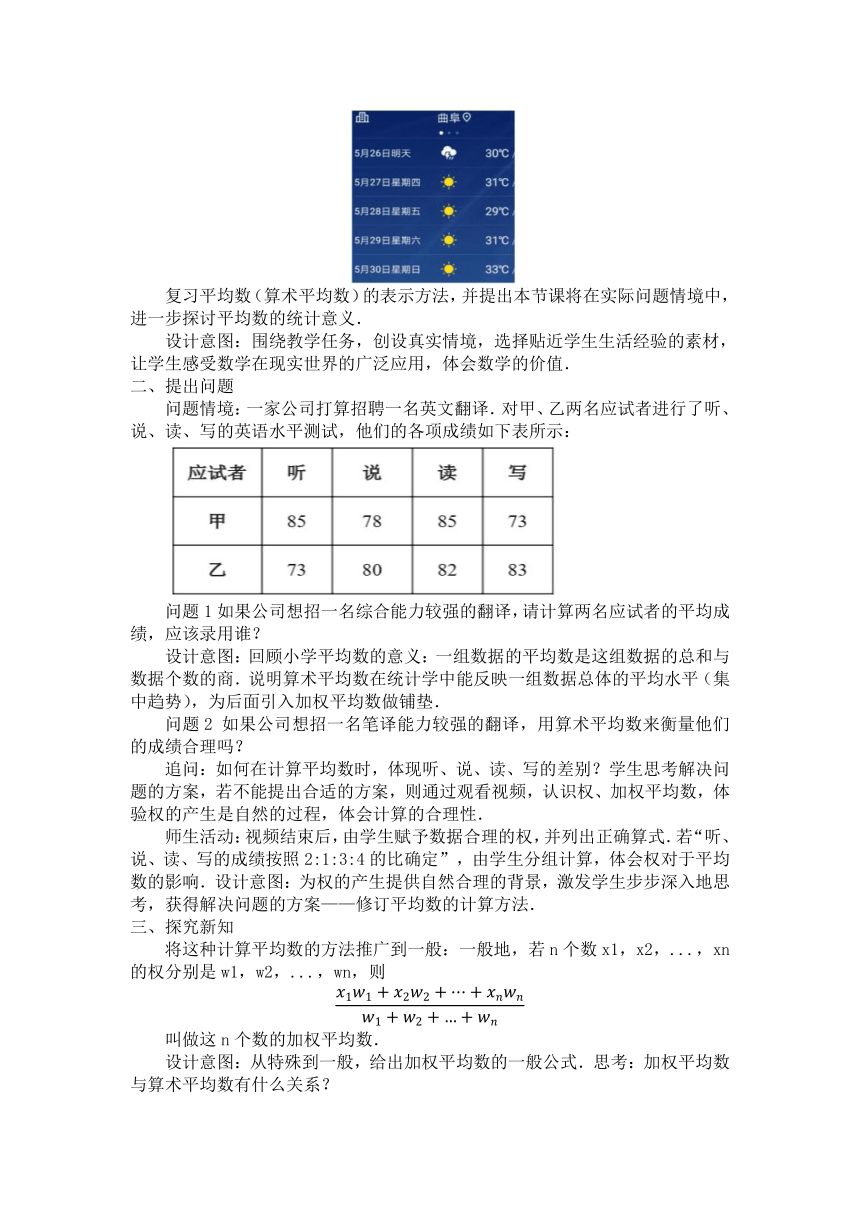
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.同学们交流从图中获取的信息,老师提出问题:如何计算出这5天的平均气温?
复习平均数(算术平均数)的表示方法,并提出本节课将在实际问题情境中,进一步探讨平均数的统计意义.
设计意图:围绕教学任务,创设真实情境,选择贴近学生生活经验的素材,让学生感受数学在现实世界的广泛应用,体会数学的价值.
二、提出问题
问题情境:一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩如下表所示:
问题1如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
设计意图:回顾小学平均数的意义:一组数据的平均数是这组数据的总和与数据个数的商.说明算术平均数在统计学中能反映一组数据总体的平均水平(集中趋势),为后面引入加权平均数做铺垫.
问题2 如果公司想招一名笔译能力较强的翻译,用算术平均数来衡量他们的成绩合理吗?
追问:如何在计算平均数时,体现听、说、读、写的差别?学生思考解决问题的方案,若不能提出合适的方案,则通过观看视频,认识权、加权平均数,体验权的产生是自然的过程,体会计算的合理性.
师生活动:视频结束后,由学生赋予数据合理的权,并列出正确算式.若“听、说、读、写的成绩按照2:1:3:4的比确定”,由学生分组计算,体会权对于平均数的影响.设计意图:为权的产生提供自然合理的背景,激发学生步步深入地思考,获得解决问题的方案——修订平均数的计算方法.
三、探究新知
将这种计算平均数的方法推广到一般:一般地,若n个数x1,x2,...,xn的权分别是w1,w2,...,wn,则
叫做这n个数的加权平均数.
设计意图:从特殊到一般,给出加权平均数的一般公式.思考:加权平均数与算术平均数有什么关系?
设计意图:帮助学生理解两种平均数的区别和联系,再一次体会权的作用.
四、理解新知
问题3如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按3:3:2:2的比确定,那么甲、乙两人谁将被录取?
师生活动:学生独立完成计算过程,共同对权的作用进行讨论:同样的一组数据,如果规定的权变化,则加权平均数随之改变.设计意图:通过比较三个结论,可以让学生体会不同的权对最后结果的影响,加深学生对权的认识.
五、应用新知
例1 一次演讲比赛中,评委按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩.试比较谁的成绩更好.
提问:演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度是用什么数据体现的?它们的权分别是什么?如何计算他们的总成绩?学生板书解答过程,师生共同订正,规范解题格式.
追问:两名选手的单项成绩都是两个95分和一个85分,为什么他们最
后的得分不同呢?
设计意图:继续以体会权的意义为目标,选取典型的生活实例为背景,通过教师指导,学生自主阅读、分析、解题,提高学生独立分析问题、解决问题的能力,并规范解题格式.通过追问,让学生进一步体会权的作用,培养学生的估算能力.
六、畅所欲言
(我来当老板)假如你开了一个广告公司,欲招聘职员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
1、公司为网络维护员、客户经理、创作总监这三种岗位各招聘一名职员,给三项成绩赋予相同的权合理吗?
2、请你设计合理的权重,为你的公司招聘一名职员.
设计意图:这是一道社会情境的数学题,让学生主动运用权影响一组数据的平均水平,帮助学生内化对权意义的理解,发展学生数据分析的观念和推理能力.
七、课堂小结
从加权平均数的意义、数据的权的意义、加权平均数公式、加权平均数与算术平均数的关系这四方面总结.
八、达标测试
1、如果数据1、4、x、5的平均数是3,那么x=.
2、某次歌唱比赛中,选手小明的唱功、音乐常识、综合知识成绩分别为88分、81分、85分.若这三项按4:3:2的比计算比赛成绩,则唱功、音乐常识、综合知识成绩的权分别为______、______和______,小明的最后成绩是______.
3、某学校规定:学生的学期总评成绩由三部分组成:平时作业、期中测验、期末测验.小明同学的平时作业、期中测验、期末测验的数学成绩依次是90分、80分、90分.
(1)若三项成绩分别按50%、20%、30%的比例计入学期总评成绩,这学期小明的数学总评成绩是多少?
(2)若三项成绩分别按5:2:3的比例计入学期总评成绩,小明的数学总评成绩是多少?
教学反思:
本节课的学习目标基本达成,当堂检测的结果也显示,大部分学生都学会了计算加权平均数,并理解了权的意义。但是也存在很多有待于提高的地方。我设计了一道招聘的开放性习题,通过让学生根据不同含义的数据赋予不同大小的“权”的活动,检验学生对于“权”的内涵理解。预设的课堂效果是学生畅所欲言,描述自己设计的录取方案,并阐述自己的理由。但是学生的积极性不高,没有达到预期的教学效果。我反思有两方面原因:
一、学生方面,学生重在学习相关的知识技能,强调计算,但应用意识薄弱,决策能力欠缺,数据观念有待加强;
二、教师方面,没有给学生留有足够的思考、创造空间,缺乏调动学生积极性的语言引导。在课堂小节部分,我的处理不妥,急于给出知识目录,让学习回顾复习,这里的教学效果不好。应该鼓励学生畅所欲言,各抒己见。学生总结为主,老师补充为辅,引导学生从知识、方法、情感等方面小结本节课所学内容。由于学生的信息技术水平有限,计算能力也有待于提高,我在备课时没有考虑使用计算器和计算机。但是大数据时代对学生的信息技术水平有更高的要求,所以在教学过程中还是应积极发挥信息技术的作用,借助信息技术进行演示,强化学生对数据的直观感受,注重信息技术与数学教学的融合。课后作业部分,可以设置一个开放性思考题:找身边的加权平均数在生活中的使用,并用自己喜欢的方法计算出结果。让学生感受到数学就在我们身边,会用数学的眼光观察现实世界,会用数学的语言表达现实世界。
教材分析:
根据《课标(2022年版)》的要求,在第二学段已经学习了有关平均数的知识.本节在复习相关内容的基础上,继续学习加权平均数、中位数和众数,并用样本的(加权)平均数、中位数、众数估计总体相应的数字特征等内容.第20.1.1小节研究加权平均数,包括权的意义、作用和不同的形式.首先,教科书设计了以招聘英文翻译为背景的实际问题,根据不同的招聘要求,各项成绩的“重要程度”不同,从而平均成绩不同,由此引入加权平均数的概念.权的重要性在于它能够反映数据的相对“重要程度”.为了更好的说明这一点,教科书设置“思考”栏目和例1,从不同方面体现权的作用,使学生更好的理解加权平均数,体会权的意义和作用.求加权平均数的问题形式多样,教科书在问题1和例1之后又介绍了两种:一是在求n个数的算术平均数时,有时会遇到重复数据较多的情况,这时可以将求算术平均数的公式进行简化,只是这里权的意义并不是很突出;二是通过一个“探究”栏目研究了对于区间分组的数据如何求加权平均数的问题,这类问题是统计中常见的.通过不同形式的问题,教科书希望学生能对加权平均数有一个全面的认识.最后教科书结合例3,介绍了如何利用样本平均数估计总体平均数的问题,使学生对抽样的必要性、样本的代表性和用样本估计总体的思想有了更深的体会.
综上所述,本节可以分为3个课时.第1课时的教学重点放在对权及加权平均数统计意义的理解.理解平均数如何刻画数据的集中趋势.分析数据时,这些统计量需要通过计算来得到,有些计算会比较复杂.统计量的复杂计算不应作为该部分教学的重点,教学中不应过分强调计算.教师应引导学生使用计算器、计算机等进行数据计算,可以与信息科技课程学习结合,开展跨学科主题学习活动,鼓励学生设计算法、编写程序来计算统计量.由于学生身处偏远农村地区,学生计算机的应用水平有限,所以统计量的计算,在课上主要是分组完成.
教学目标:
1、理解数据的权和加权平均数的统计意义.
2、掌握加权平均数的计算方法,会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析的观念.
学习重点:
对权及加权平均数统计意义的理解,会计算加权平均数.
学习难点:对权的意义理解,用加权平均数描述数据的集中趋势.
教学过程设计:
一、身边的数学
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.同学们交流从图中获取的信息,老师提出问题:如何计算出这5天的平均气温?
复习平均数(算术平均数)的表示方法,并提出本节课将在实际问题情境中,进一步探讨平均数的统计意义.
设计意图:围绕教学任务,创设真实情境,选择贴近学生生活经验的素材,让学生感受数学在现实世界的广泛应用,体会数学的价值.
二、提出问题
问题情境:一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩如下表所示:
问题1如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
设计意图:回顾小学平均数的意义:一组数据的平均数是这组数据的总和与数据个数的商.说明算术平均数在统计学中能反映一组数据总体的平均水平(集中趋势),为后面引入加权平均数做铺垫.
问题2 如果公司想招一名笔译能力较强的翻译,用算术平均数来衡量他们的成绩合理吗?
追问:如何在计算平均数时,体现听、说、读、写的差别?学生思考解决问题的方案,若不能提出合适的方案,则通过观看视频,认识权、加权平均数,体验权的产生是自然的过程,体会计算的合理性.
师生活动:视频结束后,由学生赋予数据合理的权,并列出正确算式.若“听、说、读、写的成绩按照2:1:3:4的比确定”,由学生分组计算,体会权对于平均数的影响.设计意图:为权的产生提供自然合理的背景,激发学生步步深入地思考,获得解决问题的方案——修订平均数的计算方法.
三、探究新知
将这种计算平均数的方法推广到一般:一般地,若n个数x1,x2,...,xn的权分别是w1,w2,...,wn,则
叫做这n个数的加权平均数.
设计意图:从特殊到一般,给出加权平均数的一般公式.思考:加权平均数与算术平均数有什么关系?
设计意图:帮助学生理解两种平均数的区别和联系,再一次体会权的作用.
四、理解新知
问题3如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按3:3:2:2的比确定,那么甲、乙两人谁将被录取?
师生活动:学生独立完成计算过程,共同对权的作用进行讨论:同样的一组数据,如果规定的权变化,则加权平均数随之改变.设计意图:通过比较三个结论,可以让学生体会不同的权对最后结果的影响,加深学生对权的认识.
五、应用新知
例1 一次演讲比赛中,评委按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩.试比较谁的成绩更好.
提问:演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度是用什么数据体现的?它们的权分别是什么?如何计算他们的总成绩?学生板书解答过程,师生共同订正,规范解题格式.
追问:两名选手的单项成绩都是两个95分和一个85分,为什么他们最
后的得分不同呢?
设计意图:继续以体会权的意义为目标,选取典型的生活实例为背景,通过教师指导,学生自主阅读、分析、解题,提高学生独立分析问题、解决问题的能力,并规范解题格式.通过追问,让学生进一步体会权的作用,培养学生的估算能力.
六、畅所欲言
(我来当老板)假如你开了一个广告公司,欲招聘职员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
1、公司为网络维护员、客户经理、创作总监这三种岗位各招聘一名职员,给三项成绩赋予相同的权合理吗?
2、请你设计合理的权重,为你的公司招聘一名职员.
设计意图:这是一道社会情境的数学题,让学生主动运用权影响一组数据的平均水平,帮助学生内化对权意义的理解,发展学生数据分析的观念和推理能力.
七、课堂小结
从加权平均数的意义、数据的权的意义、加权平均数公式、加权平均数与算术平均数的关系这四方面总结.
八、达标测试
1、如果数据1、4、x、5的平均数是3,那么x=.
2、某次歌唱比赛中,选手小明的唱功、音乐常识、综合知识成绩分别为88分、81分、85分.若这三项按4:3:2的比计算比赛成绩,则唱功、音乐常识、综合知识成绩的权分别为______、______和______,小明的最后成绩是______.
3、某学校规定:学生的学期总评成绩由三部分组成:平时作业、期中测验、期末测验.小明同学的平时作业、期中测验、期末测验的数学成绩依次是90分、80分、90分.
(1)若三项成绩分别按50%、20%、30%的比例计入学期总评成绩,这学期小明的数学总评成绩是多少?
(2)若三项成绩分别按5:2:3的比例计入学期总评成绩,小明的数学总评成绩是多少?
教学反思:
本节课的学习目标基本达成,当堂检测的结果也显示,大部分学生都学会了计算加权平均数,并理解了权的意义。但是也存在很多有待于提高的地方。我设计了一道招聘的开放性习题,通过让学生根据不同含义的数据赋予不同大小的“权”的活动,检验学生对于“权”的内涵理解。预设的课堂效果是学生畅所欲言,描述自己设计的录取方案,并阐述自己的理由。但是学生的积极性不高,没有达到预期的教学效果。我反思有两方面原因:
一、学生方面,学生重在学习相关的知识技能,强调计算,但应用意识薄弱,决策能力欠缺,数据观念有待加强;
二、教师方面,没有给学生留有足够的思考、创造空间,缺乏调动学生积极性的语言引导。在课堂小节部分,我的处理不妥,急于给出知识目录,让学习回顾复习,这里的教学效果不好。应该鼓励学生畅所欲言,各抒己见。学生总结为主,老师补充为辅,引导学生从知识、方法、情感等方面小结本节课所学内容。由于学生的信息技术水平有限,计算能力也有待于提高,我在备课时没有考虑使用计算器和计算机。但是大数据时代对学生的信息技术水平有更高的要求,所以在教学过程中还是应积极发挥信息技术的作用,借助信息技术进行演示,强化学生对数据的直观感受,注重信息技术与数学教学的融合。课后作业部分,可以设置一个开放性思考题:找身边的加权平均数在生活中的使用,并用自己喜欢的方法计算出结果。让学生感受到数学就在我们身边,会用数学的眼光观察现实世界,会用数学的语言表达现实世界。
