人教版四年级下册数学第七单元图形的运动(二)解答题训练(含答案)
文档属性
| 名称 | 人教版四年级下册数学第七单元图形的运动(二)解答题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版四年级下册数学第七单元 图形的运动(二)解答题训练
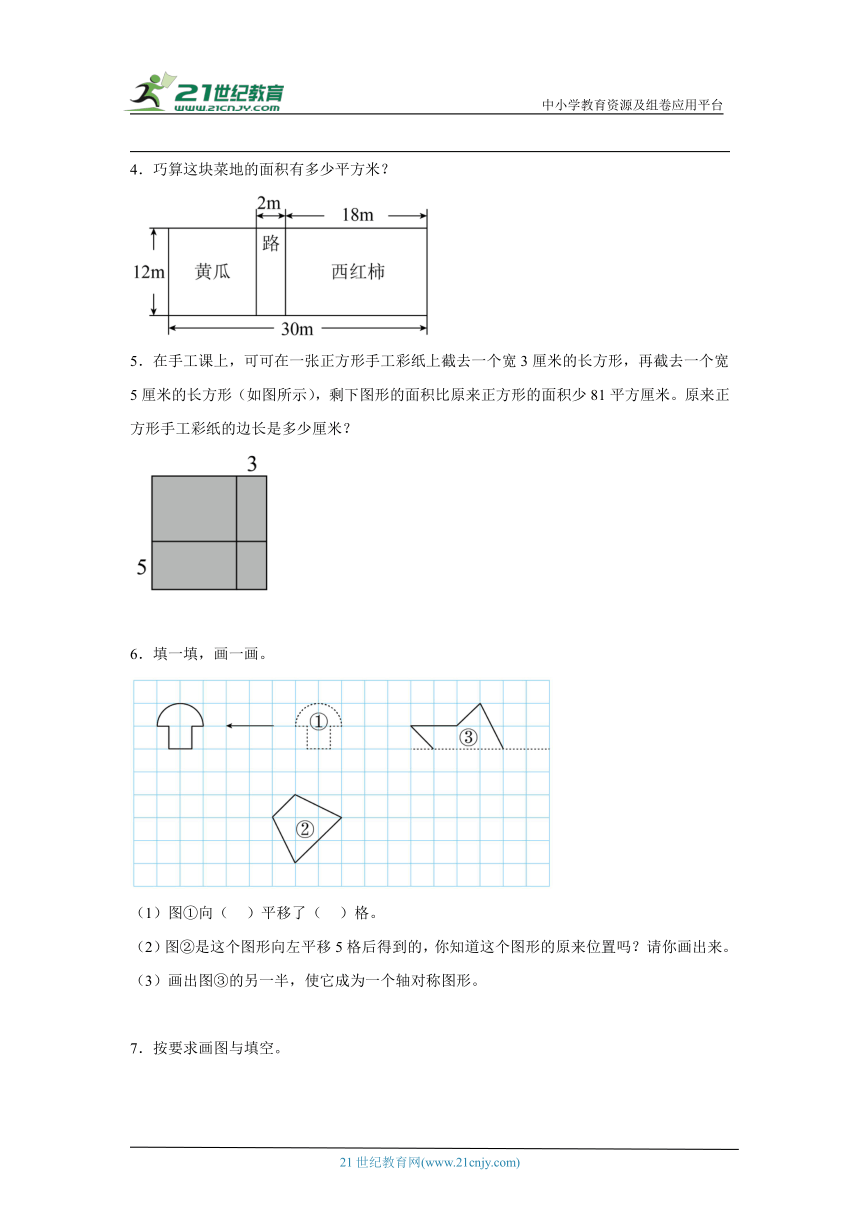
1.观察下图,画一画,填一填。
(1)画出①号三角形AC边上的高。
(2)以虚线为对称轴画出①号三角形轴对称图形的另一半。
(3)②号图形的面积是( )平方厘米。(每个小方格的边长为1厘米)
(4)画出②号图形向下平移4格后的图形。
2.填一填,画一画。
(1)图①向 平移了 格得到图②。
(2)画出图②向右平移7格后的图形。
(3)画出图③的另一半,使它成为轴对称图形。
(4)画出图④指定底边上的高。
3.下图是一个正方形,其中阴影部分是两个一样的长方形。阴影部分的周长为56厘米,求正方形的面积。
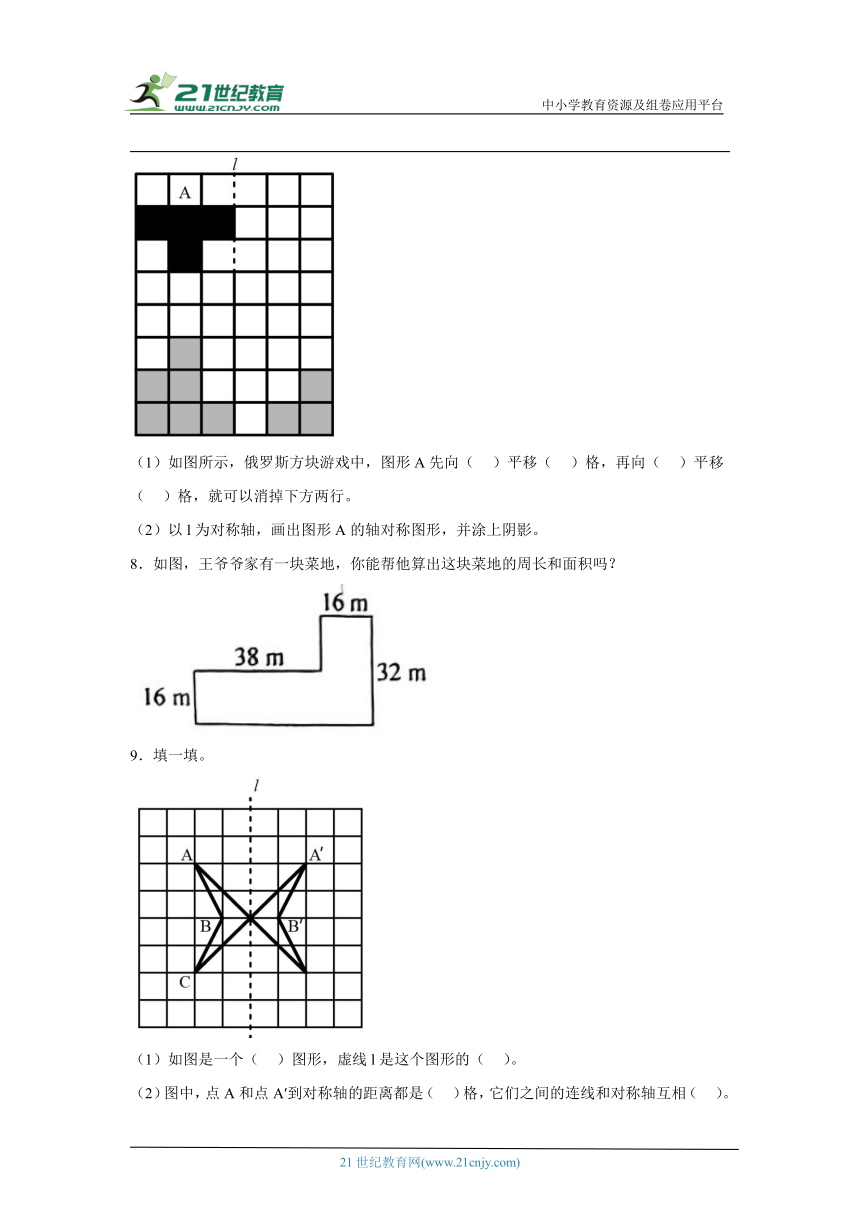
4.巧算这块菜地的面积有多少平方米?
5.在手工课上,可可在一张正方形手工彩纸上截去一个宽3厘米的长方形,再截去一个宽5厘米的长方形(如图所示),剩下图形的面积比原来正方形的面积少81平方厘米。原来正方形手工彩纸的边长是多少厘米?
6.填一填,画一画。
(1)图①向( )平移了( )格。
(2)图②是这个图形向左平移5格后得到的,你知道这个图形的原来位置吗?请你画出来。
(3)画出图③的另一半,使它成为一个轴对称图形。
7.按要求画图与填空。
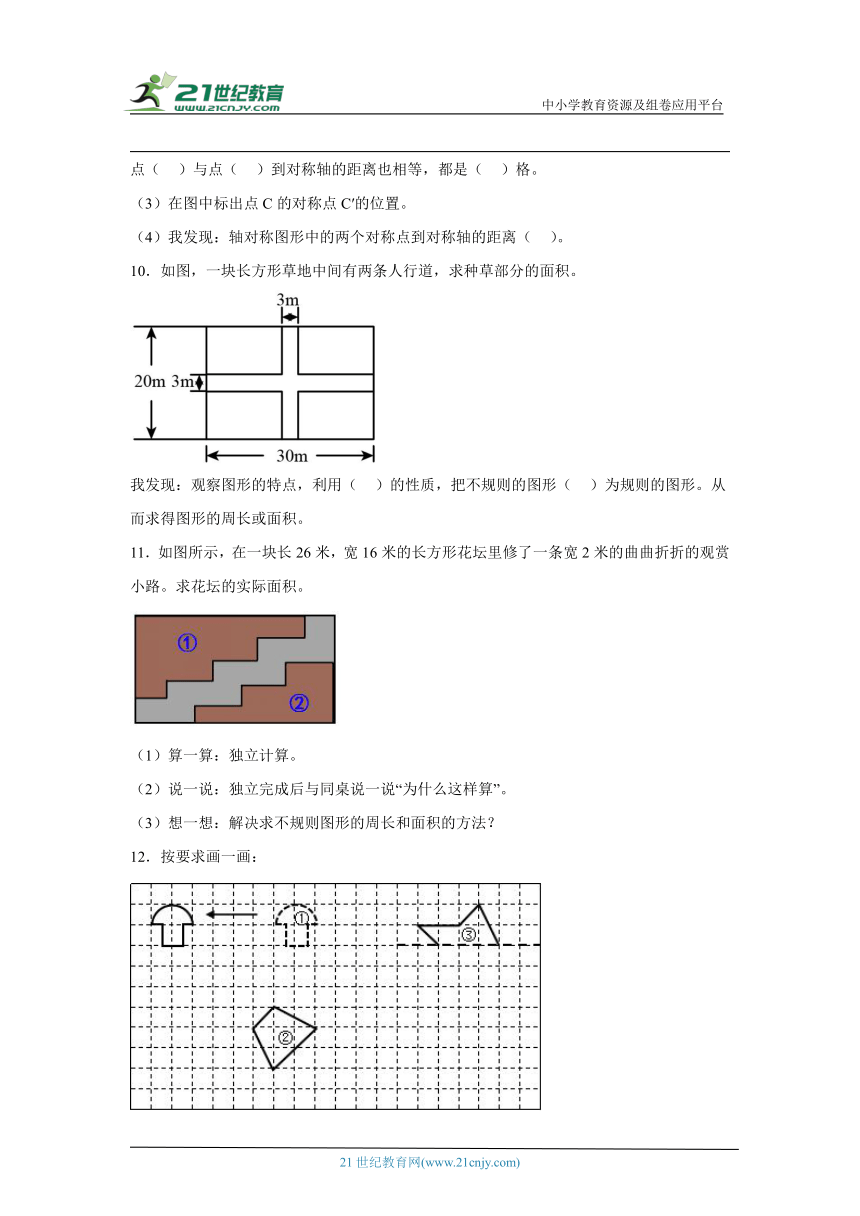
(1)如图所示,俄罗斯方块游戏中,图形A先向( )平移( )格,再向( )平移( )格,就可以消掉下方两行。
(2)以l为对称轴,画出图形A的轴对称图形,并涂上阴影。
8.如图,王爷爷家有一块菜地,你能帮他算出这块菜地的周长和面积吗?
9.填一填。
(1)如图是一个( )图形,虚线l是这个图形的( )。
(2)图中,点A和点A′到对称轴的距离都是( )格,它们之间的连线和对称轴互相( )。点( )与点( )到对称轴的距离也相等,都是( )格。
(3)在图中标出点C的对称点C′的位置。
(4)我发现:轴对称图形中的两个对称点到对称轴的距离( )。
10.如图,一块长方形草地中间有两条人行道,求种草部分的面积。
我发现:观察图形的特点,利用( )的性质,把不规则的图形( )为规则的图形。从而求得图形的周长或面积。
11.如图所示,在一块长26米,宽16米的长方形花坛里修了一条宽2米的曲曲折折的观赏小路。求花坛的实际面积。
(1)算一算:独立计算。
(2)说一说:独立完成后与同桌说一说“为什么这样算”。
(3)想一想:解决求不规则图形的周长和面积的方法?
12.按要求画一画:
(1)图①向( )平移了( )格;
(2)画出图③的另一半,使它成为一个轴对称图形;
(3)图②是一个图形向左平移5格后得到的,请你画出这个图形原来的位置。
13.下图是李明家和图书馆所在位置的平面图。李明沿着图中的实线道路,从家步行到图书馆。他前3分钟走了252米,照这样的速度,李明还要走多少分钟才能到达图书馆?
14.根据要求画图并填空。(方格图中每个小正方形边长1cm)
(1)画出上图图形①所标出底边上的高,这条高是( )cm。
(2)画出图形①向下平移4格后的图形。
(3)画出图②这个轴对称图形的另一半。
15.按要求在方格纸上画一画。(每个小方格的面积表示1平方厘米)
(1)图A的周长是( )厘米,面积是( )平方厘米。
(2)将图A先向上平移3格,再向右平移2格,得到图形B。
(3)在方格纸的空白处画一个面积是12平方厘米的长方形。
16.下面每个小方格都是边长1厘米的正方形,请按要求画一画,填一填。
(1)根据A图的对称轴补全图A这个对称轴图形。
(2)图B的面积是( )平方厘米。
(3)画出图C向右平移6格后的图形。
17.按要求完成下面4个小题。
(1)图①向( )平移了( )格。
(2)图②是某个图形向左平移5格后得到的。你知道这个图形原来的位置吗?请你画出来。
(3)画出图③的另一半,使它成为一个轴对称图形。
(4)图④的面积是( )平方厘米。
18.(1)根据对称轴补全下面这个轴对称图形。
(2)画出这个轴对称图形向右平移6格后的图形。
(3)如果每个小方格的面积是,这个轴对称图形的面积是( )。
19.在下面图形中,你还能画出其他对称轴吗?如果能,请画出来。
( )条对称轴 ( )条对称轴
( )条对称轴 ( )条对称轴
( )条对称轴 ( )条对称轴
20.下图是小明家的长方形花坛,空白部分用于种花,涂色部分(一大一小的正方形)用于种草。已知大正方形的面积为,小正方形的面积为。空白部分的面积是多少平方米?
21.一块长方形草地长,宽,中间有两条小路(如下图)。这两条小路的总面积是多少?现在要给这两条小路铺上一层鹅卵石,平均每平方米约需鹅卵石,大约共需多少千克鹅卵石?
22.下图是一块长方形公园的示意图,它的长是,宽是,其中涂色部分是绿地,中间有一条宽为的小路,求绿地的面积。
23.在一个长30m,宽14m的长方形草坪上有两条相交的小路,那么草坪的面积是多少平方米?
24.图中的方格都是边长为1cm的正方形,AB是平行四边形ACEF的一条高。
(1)把三角形ABC向右平移5格,画出平移后的图形,并把四边形ABEF以及平移后的图形涂上颜色。
(2)平移后的三角形与四边形ABEF拼成了一个( )形,拼成的这个图形的面积是( )cm2,所以原来平行四边形ACEF的面积是( )cm2。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)、(2)、(4)均见详解
(3)6;
【分析】(1)把三角板的一直角边靠紧三角形的AC边,沿三角形的AC边滑动三角板,当另一直角边经过三角形底边相对的顶点B点时,沿这条直角边画的顶点到底边的垂直线段就是该三角形的高,高用虚线表示,依此画图并标上垂直符号即可。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可。
(3)通过平移可知,②号图形的面积等于长3厘米、宽2厘米的长方形的面积(如下图所示),长方形的面积=长×宽,依此计算。
(4)找出构成图形的关键点,确定平移方向(向下)和平移距离(4格) ,由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
【详解】(1)、(2)、(4)画图如下:
(3)3×2=6(平方厘米),即②号图形的面积是6平方厘米。
【点睛】解答此题的关键是要熟练掌握三角形的高的画法,补全轴对称图形的方法,作平移后的图形的方法,以及利用平移的方法计算图形的面积。
2.(1)下;4;
(2)见详解;
(3)见详解;
(4)见详解
【分析】(1)根据平移的方向和距离,解答此题即可;
(2)根据平移的特征,把图形②的各顶点分别向右平移7格,依次连接即可得到平移后的图形;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出上半图的关键对称点,依次连接即可补全这个轴对称图形的另一半;
(4)根据三角形高的画法,画出高即可。
【详解】(1)观察图形可知:图①向下平移了4格得到图②;
(2)画出图②向右平移7格后的图形,如下;
(3)画出图③的另一半,使它成为轴对称图形,如下;
(4)画出图④指定底边上的高,如下:
【点睛】熟练掌握平移规律和轴对称图形的定义,是解答此题的关键。
3.196平方厘米
【分析】将阴影部分的周长按照下图进行转化,发现阴影部分的周长就是正方形的周长。根据正方形的边长=周长÷4得出正方形的边长是14厘米,正方形的面积=边长×边长。
【详解】56÷4=14(厘米)
14×14=196(平方厘米)
答:正方形的面积196平方厘米。
4.336平方米
【分析】如下图,把路平移到右边,西红柿菜地平移到与黄瓜菜地连在一起,求菜地的面积就等于求长为(30-2)米,宽为12米的长方形的面积,长方形的面积=长×宽,把数据代入计算即可解答。
【详解】(30-2)×12
=28×12
=336(平方米)
答:这块菜地的面积有336平方米。
5.12厘米
【分析】
由图可知减少的部分的面积是长方形①+长方形②+长方形③的面积,③是一个长5厘米,宽3厘米的长方形,即长方形③的面积为3×5,把长方形①移到图②所在的位置,下面长方形的面积等于③的面积,此时4个小长方形合成一个宽为3+5=8厘米,长为正方形边长的新长方形,新长方形的面积=长方形①+长方形②+长方形③+3×5,求出长方形的面积,然后除以宽,即可求出原来正方形手工彩纸的边长是多少厘米。
【详解】(81+3×5)÷(3十5)
=(81+15)÷(3十5)
=96÷(3十5)
=96÷8
=12(厘米)
答:原来正方形手工彩纸的边长是12厘米。
6.(1)左;6
(2)(3)见详解
【分析】(1)找出原来蘑菇上的一个点和平移后蘑菇对应的点,数一数即可得出移动的格子数,再根据常识判断是向左还是向右;
(2)因为图②是这个图形向左平移5格后得到的,找出图②中的顶点,分别向右数出5格画出对应点,然后连接各点画出图形即可;
(3)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴是对称点的连线的垂直平分线,在对称轴的另一边画出图形的几个顶点,再依次连线即可。
【详解】由分析可得:
(1)图①向左平移了6格。
(2)(3)画图如下:
【点睛】本题考查了作轴对称图形和作平移后的图形,以上知识都需要熟练掌握并且灵活运用,尤其需要能结合知识准确画图。
7.(1)右;2;下;5;(2)见详解
【分析】(1)先找出构成图形的关键点,然后再确定平移方向和平移距离即可。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接并涂上阴影即可。
【详解】(1)根据分析可知,图形A先向右平移2格,再向下平移5格,就可以消掉下方两行。
(2)画图如下:
【点睛】解答此题的关键是要熟练掌握补全轴对称图形的方法,以及掌握作平移后的图形的方法。
8.172米;1120平方米
【分析】如图①,将图形分割成两个长方形,再根据长方形面积=长×宽,将两个长方形的面积相加即可。
如图②,将这块菜地的两条边向上向左平移,菜地的周长就是长(38+16)米宽32米的长方形的周长。长方形的周长=(长+宽)×2,代入数据计算即可。
①②
【详解】长方形的面积=16×32+38×16
=(32+38)×16
=70×16
=1120(平方米)
长方形的周长=(38+16+32)×2
=86×2
=172(米)
答:这块菜地的周长和面积分别为172米和1120平方米。
9.(1)轴对称;对称轴
(2)2;垂直;B;B′;1
(3)见详解
(4)相等
【分析】(1)一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。据此可知,这个图形是一个轴对称图形,虚线l是这个图形的对称轴。
(2)轴对称图形中,对称点到对称轴的距离相等,对称点的连线与对称轴互相垂直。据此解答。
(3)根据轴对称的定义可知,点C和对称点C′到虚线1的距离相等,且这两个点的连线与对称轴互相垂直,据此标出点C的对称点C′的位置。
(4)轴对称图形中的两个对称点到对称轴的距离相等。
【详解】(1)如图是一个轴对称图形,虚线l是这个图形的对称轴。
(2)图中,点A和点A′到对称轴的距离都是2格,它们之间的连线和对称轴互相垂直。点B与点B′到对称轴的距离也相等,都是1格。
(3)
(4)我发现:轴对称图形中的两个对称点到对称轴的距离相等。
【点睛】本题考查轴对称的认识,关键是明确对称点到对称轴的距离相等,对称点的连线与对称轴互相垂直。
10.平移;转换,面积为459平方米
【分析】观察题图,可利用平移,将这两条人行道分别向上向左平移,原来种草部分的面积就等于长(30-3)米,宽(20-3)米的长方形的面积。再根据长方形的面积=长×宽解答。
【详解】
(30-3)×(20-3)
=27×17
=459(平方米)
答:种草部分的面积是459平方米。(答案不唯一)
我发现:观察图形的特点,利用平移的性质,把不规则的图形转换为规则的图形。从而求得图形的周长或面积。
【点睛】本题考查利用平移巧算周长和面积,常利用平移把不规则的图形转换为规则的图形,再根据长方形、正方形的周长、面积公式等进行解答。
11.(1)336平方米;
(2)见详解
(3)见详解
【分析】(1)观察图形,通过平移可知,花坛的面积相当于一个长(26-2)米、宽(16-2)米的长方形的面积;根据“长方形面积=长×宽”,即可求出花坛的面积。
(2)如下图:将②先向上平移2米,再向左平移2米,①和②可以拼成如图所示的一个长方形,拼成的长方形的长是(26-2)米、宽是(16-2)米,根据长方形面积计算公式可知,花坛的实际面积=①、②两部分拼成的长方形的面积=(26-2)×(16-2)。
(3)求不规则图形的周长和面积时,可以利用平移把不规则图形的周长和面积转化成长方形、正方形等规则图形的周长和面积,再利用长方形、正方形底周长和面积计算公式求解即可。
【详解】(1)(26-2)×(16-2)
=24×14
=336(平方米)
答:这个花坛的面积是336平方米。
(2)如图:,将②先向上平移2米,再向左平移2米,花坛拼成了一个长是(26-2)米、宽是(16-2)米的长方形;
答:通过平移,花坛的实际面积=①、②两部分拼成的长方形的面积=(26-2)×(16-2)。
(3)答:解决求不规则图形的周长和面积的方法:可以利用平移把不规则图形的周长和面积转化成长方形、正方形等规则图形的周长和面积。
【点睛】熟练掌握把不规则图形的周长和面积转换成规则图形的周长和面积的方法,是解答此题的关键。
12.(1)左;6;(2)见详解;(3)见详解
【分析】(1)根据图①虚线与实线图形的相对位置及箭头指向、对应部分之间的距离(格数)即可确定平移的方向和距离(格数)。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图③的关键对称点,依次连接即可。
(3)想要画出图②原来的位置,则要将图②向右平移5格,根据平移的特征,把图2的各顶点分别向右平移5格,依次连接即可得到原来的位置。
【详解】(1)图①向左平移了6格;
(2)画出图③的另一半,使它成为一个轴对称图形如下图;
(3)图②是一个图形向左平移5格得到的,“我”知道这个图形的原来位置,如下图:
【点睛】图形平移注意三要素:即原位置、平移方向、平移距离。求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连接各对称点即可。
13.6分钟
【分析】根据图示,利用平移的方法可得李明走的路程等于长方形的长和宽的和;然后根据路程÷时间=速度,用252除以3,求出他每分钟走多少米;最后用剩下的路程除以他的速度,即可求出李明还要走多少分钟才能到达图书馆。
【详解】(450+306-252)÷(252÷3)
=(756-252)÷84
=504÷84
=6(分钟)
答:李明还要走6分钟才能到达图书馆。
【点睛】本题考查的知识点:①平移求总路程;②行程问题。行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
14.(1)见详解;3;
(2)、(3)见详解
【分析】(1)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图;这条高有几个小正方形边长的长度,就是几厘米。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出图②右边图形的关键对称点,依次连接即可。
【详解】(1)画图如下,这条高是3cm。
(2)、(3)画图如下:
【点睛】此题考查的是三角形的高及画法、补全轴对称图形,以及作平移后的图形,应熟练掌握。
15.(1)10;4
(2)(3)见详解
【分析】(1)根据周长的意义:封闭图形一周的长度叫做图形的周长可知,图A的周长是10个小方格的边长和,即10厘米。根据面积的意义:面积是图形所占平面的大小可知,图A的面积是4个小方格的面积和,即4平方厘米。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)根据长方形的面积=长×宽,以及6×2=12,可知面积是12平方厘米的长方形,可以是长6厘米宽2厘米。
【详解】(1)图A的周长是10厘米,面积是4平方厘米。
(2)(3)
【点睛】作平移后图形时,确定图形的关键点及对应点是解题的关键。画已知面积的长方形时,关键是根据面积公式求出长方形的长与宽。
16.(1)、(3)均见详解
(2)16
【分析】(1)一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;折叠的这条直线叫做这个图形的对称轴,依此补全轴对称图形;
(2)通过平移,将这个图形变成一个长为8厘米,宽为2厘米的长方形(图见详解),长方形的面积=长×宽,依此计算出这个图形的面积即可;
(3)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画图即可。
【详解】(1)、(3)画图如下:
(2)通过平移,如下图所示:
8×2=16(平方厘米)
【点睛】此图考查的是利用平移的方法计算图形的周长,补全轴对称图形,以及作平移后的图形,应熟练掌握。
17.(1)左;6
(2)(3)见详解
(4)12
【分析】(1)从图①中找出一个关键点,再在平移后的图形中找出这个关键点的对应点,观察这两个点之间的位置关系可知,图①向左平移了6格。
(2)图②是某个图形向左平移5格后得到的,则将图②向右平移5格后得到这个图形。
(3)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(4)图④中有9个完整的小方格和6个不完整的小方格,每个不完整的小方格的面积按照完整小方格面积的一半计算,则图④的面积是(9+6÷2)平方厘米。
【详解】(1)图①向左平移了6格。
(2)(3)
(4)9+6÷2
=9+3
=12(平方厘米)
图④的面积是12平方厘米。
【点睛】补全轴对称图形和作平移后图形时,确定图形的关键点及对称点或对应点是解题的关键。用数格子估计不规则图形面积时,注意把不完整格按半格计算,再加上整数格,估算出面积。
18.(1)(2)见详解;(3)10
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)观察这个轴对称图形可知,图形里面有8个完整的小方格,和4个不完整的小方格,每个不完整的小方格按照半个方格的面积计算,则轴对称图形的面积是(8+4÷2)。
【详解】(1)(2)
(3)8+4÷2
=8+2
=10()
则这个轴对称图形的面积是10。
【点睛】补全轴对称图形和作平移后图形时,确定图形的关键点及对称点或对应点是解决本题的关键。求不规则图形面积时,分别数出完整格数和不完整格数,把不完整格按半格计算,再加上整数格,即可求出图形的面积。
19.见详解
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行解答。
【详解】
(1)条对称轴 (5)条对称轴
(2)条对称轴 (2)条对称轴
(1)条对称轴 (6)条对称轴
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
20.
【分析】涂色部分的大正方形面积是,所以大正方形的边长是;涂色部分的小正方形的面积是,所以小正方形的边长是。题图中的空白部分与小正方形合起来就是一个长为、宽为的长方形,用这个长方形的面积减去小正方形的面积即为空白部分的面积。
【详解】49=7×7
9=3×3
7×3-9
=21-9
=12(m2)
答:空白部分的面积是。
【点睛】熟练掌握正方形和长方形的面积公式是解答本题的关键。
21.;
【分析】题图中的两条小路经过平移后就是一个长为、宽为的长方形,然后利用长方形的面积公式求出两条小路的总面积,再乘30就是一共需要的鹅卵石质量。
【详解】
答:这两条小路的总面积是,大约共需鹅卵石。
【点睛】两条小路的面积和与长20m、宽4m的长方形面积相等,这是解答本题的关键。
22.
【分析】把题图中的小路分别平移到公园的边沿,水平方向的向上平移,竖直方向的向左平移,这样绿地就变成了一个长方形,其中长是,宽是。再根据长方形的面积=长×宽,求出绿地的面积。
【详解】
答:绿地的面积是。
【点睛】本题考查利用平移求图形的面积,通过平移将求不规则图形的面积转换为求规则图形的面积,再根据长方形的面积公式解答即可。
23.377 m2
【详解】(30-1)×(14-1)=377(m2)
答:草坪的面积是377 m2。
24.(1)见详解
(2)长方;15;15
【分析】(1)平移三角形时平移ABC三个点,然后再连接即可,根据要求涂色即可。
(2)根据(1)中得到的图形判断平行后的图形,并根据对应公式计算面积,平移是改变位置,但不改变大小,所以平移前后面积不变。
【详解】(1)如图:
(2)平移后的三角形与四边形ABEF拼成了一个长方形,
长方形的面积=长×宽=3×5=15(cm2),所以平行四边形的面积也是15cm2。
【点睛】本题考查图形的平移及长方形的面积。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版四年级下册数学第七单元 图形的运动(二)解答题训练
1.观察下图,画一画,填一填。
(1)画出①号三角形AC边上的高。
(2)以虚线为对称轴画出①号三角形轴对称图形的另一半。
(3)②号图形的面积是( )平方厘米。(每个小方格的边长为1厘米)
(4)画出②号图形向下平移4格后的图形。
2.填一填,画一画。
(1)图①向 平移了 格得到图②。
(2)画出图②向右平移7格后的图形。
(3)画出图③的另一半,使它成为轴对称图形。
(4)画出图④指定底边上的高。
3.下图是一个正方形,其中阴影部分是两个一样的长方形。阴影部分的周长为56厘米,求正方形的面积。
4.巧算这块菜地的面积有多少平方米?
5.在手工课上,可可在一张正方形手工彩纸上截去一个宽3厘米的长方形,再截去一个宽5厘米的长方形(如图所示),剩下图形的面积比原来正方形的面积少81平方厘米。原来正方形手工彩纸的边长是多少厘米?
6.填一填,画一画。
(1)图①向( )平移了( )格。
(2)图②是这个图形向左平移5格后得到的,你知道这个图形的原来位置吗?请你画出来。
(3)画出图③的另一半,使它成为一个轴对称图形。
7.按要求画图与填空。
(1)如图所示,俄罗斯方块游戏中,图形A先向( )平移( )格,再向( )平移( )格,就可以消掉下方两行。
(2)以l为对称轴,画出图形A的轴对称图形,并涂上阴影。
8.如图,王爷爷家有一块菜地,你能帮他算出这块菜地的周长和面积吗?
9.填一填。
(1)如图是一个( )图形,虚线l是这个图形的( )。
(2)图中,点A和点A′到对称轴的距离都是( )格,它们之间的连线和对称轴互相( )。点( )与点( )到对称轴的距离也相等,都是( )格。
(3)在图中标出点C的对称点C′的位置。
(4)我发现:轴对称图形中的两个对称点到对称轴的距离( )。
10.如图,一块长方形草地中间有两条人行道,求种草部分的面积。
我发现:观察图形的特点,利用( )的性质,把不规则的图形( )为规则的图形。从而求得图形的周长或面积。
11.如图所示,在一块长26米,宽16米的长方形花坛里修了一条宽2米的曲曲折折的观赏小路。求花坛的实际面积。
(1)算一算:独立计算。
(2)说一说:独立完成后与同桌说一说“为什么这样算”。
(3)想一想:解决求不规则图形的周长和面积的方法?
12.按要求画一画:
(1)图①向( )平移了( )格;
(2)画出图③的另一半,使它成为一个轴对称图形;
(3)图②是一个图形向左平移5格后得到的,请你画出这个图形原来的位置。
13.下图是李明家和图书馆所在位置的平面图。李明沿着图中的实线道路,从家步行到图书馆。他前3分钟走了252米,照这样的速度,李明还要走多少分钟才能到达图书馆?
14.根据要求画图并填空。(方格图中每个小正方形边长1cm)
(1)画出上图图形①所标出底边上的高,这条高是( )cm。
(2)画出图形①向下平移4格后的图形。
(3)画出图②这个轴对称图形的另一半。
15.按要求在方格纸上画一画。(每个小方格的面积表示1平方厘米)
(1)图A的周长是( )厘米,面积是( )平方厘米。
(2)将图A先向上平移3格,再向右平移2格,得到图形B。
(3)在方格纸的空白处画一个面积是12平方厘米的长方形。
16.下面每个小方格都是边长1厘米的正方形,请按要求画一画,填一填。
(1)根据A图的对称轴补全图A这个对称轴图形。
(2)图B的面积是( )平方厘米。
(3)画出图C向右平移6格后的图形。
17.按要求完成下面4个小题。
(1)图①向( )平移了( )格。
(2)图②是某个图形向左平移5格后得到的。你知道这个图形原来的位置吗?请你画出来。
(3)画出图③的另一半,使它成为一个轴对称图形。
(4)图④的面积是( )平方厘米。
18.(1)根据对称轴补全下面这个轴对称图形。
(2)画出这个轴对称图形向右平移6格后的图形。
(3)如果每个小方格的面积是,这个轴对称图形的面积是( )。
19.在下面图形中,你还能画出其他对称轴吗?如果能,请画出来。
( )条对称轴 ( )条对称轴
( )条对称轴 ( )条对称轴
( )条对称轴 ( )条对称轴
20.下图是小明家的长方形花坛,空白部分用于种花,涂色部分(一大一小的正方形)用于种草。已知大正方形的面积为,小正方形的面积为。空白部分的面积是多少平方米?
21.一块长方形草地长,宽,中间有两条小路(如下图)。这两条小路的总面积是多少?现在要给这两条小路铺上一层鹅卵石,平均每平方米约需鹅卵石,大约共需多少千克鹅卵石?
22.下图是一块长方形公园的示意图,它的长是,宽是,其中涂色部分是绿地,中间有一条宽为的小路,求绿地的面积。
23.在一个长30m,宽14m的长方形草坪上有两条相交的小路,那么草坪的面积是多少平方米?
24.图中的方格都是边长为1cm的正方形,AB是平行四边形ACEF的一条高。
(1)把三角形ABC向右平移5格,画出平移后的图形,并把四边形ABEF以及平移后的图形涂上颜色。
(2)平移后的三角形与四边形ABEF拼成了一个( )形,拼成的这个图形的面积是( )cm2,所以原来平行四边形ACEF的面积是( )cm2。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)、(2)、(4)均见详解
(3)6;
【分析】(1)把三角板的一直角边靠紧三角形的AC边,沿三角形的AC边滑动三角板,当另一直角边经过三角形底边相对的顶点B点时,沿这条直角边画的顶点到底边的垂直线段就是该三角形的高,高用虚线表示,依此画图并标上垂直符号即可。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可。
(3)通过平移可知,②号图形的面积等于长3厘米、宽2厘米的长方形的面积(如下图所示),长方形的面积=长×宽,依此计算。
(4)找出构成图形的关键点,确定平移方向(向下)和平移距离(4格) ,由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
【详解】(1)、(2)、(4)画图如下:
(3)3×2=6(平方厘米),即②号图形的面积是6平方厘米。
【点睛】解答此题的关键是要熟练掌握三角形的高的画法,补全轴对称图形的方法,作平移后的图形的方法,以及利用平移的方法计算图形的面积。
2.(1)下;4;
(2)见详解;
(3)见详解;
(4)见详解
【分析】(1)根据平移的方向和距离,解答此题即可;
(2)根据平移的特征,把图形②的各顶点分别向右平移7格,依次连接即可得到平移后的图形;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出上半图的关键对称点,依次连接即可补全这个轴对称图形的另一半;
(4)根据三角形高的画法,画出高即可。
【详解】(1)观察图形可知:图①向下平移了4格得到图②;
(2)画出图②向右平移7格后的图形,如下;
(3)画出图③的另一半,使它成为轴对称图形,如下;
(4)画出图④指定底边上的高,如下:
【点睛】熟练掌握平移规律和轴对称图形的定义,是解答此题的关键。
3.196平方厘米
【分析】将阴影部分的周长按照下图进行转化,发现阴影部分的周长就是正方形的周长。根据正方形的边长=周长÷4得出正方形的边长是14厘米,正方形的面积=边长×边长。
【详解】56÷4=14(厘米)
14×14=196(平方厘米)
答:正方形的面积196平方厘米。
4.336平方米
【分析】如下图,把路平移到右边,西红柿菜地平移到与黄瓜菜地连在一起,求菜地的面积就等于求长为(30-2)米,宽为12米的长方形的面积,长方形的面积=长×宽,把数据代入计算即可解答。
【详解】(30-2)×12
=28×12
=336(平方米)
答:这块菜地的面积有336平方米。
5.12厘米
【分析】
由图可知减少的部分的面积是长方形①+长方形②+长方形③的面积,③是一个长5厘米,宽3厘米的长方形,即长方形③的面积为3×5,把长方形①移到图②所在的位置,下面长方形的面积等于③的面积,此时4个小长方形合成一个宽为3+5=8厘米,长为正方形边长的新长方形,新长方形的面积=长方形①+长方形②+长方形③+3×5,求出长方形的面积,然后除以宽,即可求出原来正方形手工彩纸的边长是多少厘米。
【详解】(81+3×5)÷(3十5)
=(81+15)÷(3十5)
=96÷(3十5)
=96÷8
=12(厘米)
答:原来正方形手工彩纸的边长是12厘米。
6.(1)左;6
(2)(3)见详解
【分析】(1)找出原来蘑菇上的一个点和平移后蘑菇对应的点,数一数即可得出移动的格子数,再根据常识判断是向左还是向右;
(2)因为图②是这个图形向左平移5格后得到的,找出图②中的顶点,分别向右数出5格画出对应点,然后连接各点画出图形即可;
(3)根据轴对称图形的性质,对称点到对称轴的距离相等,对称轴是对称点的连线的垂直平分线,在对称轴的另一边画出图形的几个顶点,再依次连线即可。
【详解】由分析可得:
(1)图①向左平移了6格。
(2)(3)画图如下:
【点睛】本题考查了作轴对称图形和作平移后的图形,以上知识都需要熟练掌握并且灵活运用,尤其需要能结合知识准确画图。
7.(1)右;2;下;5;(2)见详解
【分析】(1)先找出构成图形的关键点,然后再确定平移方向和平移距离即可。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接并涂上阴影即可。
【详解】(1)根据分析可知,图形A先向右平移2格,再向下平移5格,就可以消掉下方两行。
(2)画图如下:
【点睛】解答此题的关键是要熟练掌握补全轴对称图形的方法,以及掌握作平移后的图形的方法。
8.172米;1120平方米
【分析】如图①,将图形分割成两个长方形,再根据长方形面积=长×宽,将两个长方形的面积相加即可。
如图②,将这块菜地的两条边向上向左平移,菜地的周长就是长(38+16)米宽32米的长方形的周长。长方形的周长=(长+宽)×2,代入数据计算即可。
①②
【详解】长方形的面积=16×32+38×16
=(32+38)×16
=70×16
=1120(平方米)
长方形的周长=(38+16+32)×2
=86×2
=172(米)
答:这块菜地的周长和面积分别为172米和1120平方米。
9.(1)轴对称;对称轴
(2)2;垂直;B;B′;1
(3)见详解
(4)相等
【分析】(1)一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。据此可知,这个图形是一个轴对称图形,虚线l是这个图形的对称轴。
(2)轴对称图形中,对称点到对称轴的距离相等,对称点的连线与对称轴互相垂直。据此解答。
(3)根据轴对称的定义可知,点C和对称点C′到虚线1的距离相等,且这两个点的连线与对称轴互相垂直,据此标出点C的对称点C′的位置。
(4)轴对称图形中的两个对称点到对称轴的距离相等。
【详解】(1)如图是一个轴对称图形,虚线l是这个图形的对称轴。
(2)图中,点A和点A′到对称轴的距离都是2格,它们之间的连线和对称轴互相垂直。点B与点B′到对称轴的距离也相等,都是1格。
(3)
(4)我发现:轴对称图形中的两个对称点到对称轴的距离相等。
【点睛】本题考查轴对称的认识,关键是明确对称点到对称轴的距离相等,对称点的连线与对称轴互相垂直。
10.平移;转换,面积为459平方米
【分析】观察题图,可利用平移,将这两条人行道分别向上向左平移,原来种草部分的面积就等于长(30-3)米,宽(20-3)米的长方形的面积。再根据长方形的面积=长×宽解答。
【详解】
(30-3)×(20-3)
=27×17
=459(平方米)
答:种草部分的面积是459平方米。(答案不唯一)
我发现:观察图形的特点,利用平移的性质,把不规则的图形转换为规则的图形。从而求得图形的周长或面积。
【点睛】本题考查利用平移巧算周长和面积,常利用平移把不规则的图形转换为规则的图形,再根据长方形、正方形的周长、面积公式等进行解答。
11.(1)336平方米;
(2)见详解
(3)见详解
【分析】(1)观察图形,通过平移可知,花坛的面积相当于一个长(26-2)米、宽(16-2)米的长方形的面积;根据“长方形面积=长×宽”,即可求出花坛的面积。
(2)如下图:将②先向上平移2米,再向左平移2米,①和②可以拼成如图所示的一个长方形,拼成的长方形的长是(26-2)米、宽是(16-2)米,根据长方形面积计算公式可知,花坛的实际面积=①、②两部分拼成的长方形的面积=(26-2)×(16-2)。
(3)求不规则图形的周长和面积时,可以利用平移把不规则图形的周长和面积转化成长方形、正方形等规则图形的周长和面积,再利用长方形、正方形底周长和面积计算公式求解即可。
【详解】(1)(26-2)×(16-2)
=24×14
=336(平方米)
答:这个花坛的面积是336平方米。
(2)如图:,将②先向上平移2米,再向左平移2米,花坛拼成了一个长是(26-2)米、宽是(16-2)米的长方形;
答:通过平移,花坛的实际面积=①、②两部分拼成的长方形的面积=(26-2)×(16-2)。
(3)答:解决求不规则图形的周长和面积的方法:可以利用平移把不规则图形的周长和面积转化成长方形、正方形等规则图形的周长和面积。
【点睛】熟练掌握把不规则图形的周长和面积转换成规则图形的周长和面积的方法,是解答此题的关键。
12.(1)左;6;(2)见详解;(3)见详解
【分析】(1)根据图①虚线与实线图形的相对位置及箭头指向、对应部分之间的距离(格数)即可确定平移的方向和距离(格数)。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图③的关键对称点,依次连接即可。
(3)想要画出图②原来的位置,则要将图②向右平移5格,根据平移的特征,把图2的各顶点分别向右平移5格,依次连接即可得到原来的位置。
【详解】(1)图①向左平移了6格;
(2)画出图③的另一半,使它成为一个轴对称图形如下图;
(3)图②是一个图形向左平移5格得到的,“我”知道这个图形的原来位置,如下图:
【点睛】图形平移注意三要素:即原位置、平移方向、平移距离。求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连接各对称点即可。
13.6分钟
【分析】根据图示,利用平移的方法可得李明走的路程等于长方形的长和宽的和;然后根据路程÷时间=速度,用252除以3,求出他每分钟走多少米;最后用剩下的路程除以他的速度,即可求出李明还要走多少分钟才能到达图书馆。
【详解】(450+306-252)÷(252÷3)
=(756-252)÷84
=504÷84
=6(分钟)
答:李明还要走6分钟才能到达图书馆。
【点睛】本题考查的知识点:①平移求总路程;②行程问题。行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
14.(1)见详解;3;
(2)、(3)见详解
【分析】(1)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图;这条高有几个小正方形边长的长度,就是几厘米。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出图②右边图形的关键对称点,依次连接即可。
【详解】(1)画图如下,这条高是3cm。
(2)、(3)画图如下:
【点睛】此题考查的是三角形的高及画法、补全轴对称图形,以及作平移后的图形,应熟练掌握。
15.(1)10;4
(2)(3)见详解
【分析】(1)根据周长的意义:封闭图形一周的长度叫做图形的周长可知,图A的周长是10个小方格的边长和,即10厘米。根据面积的意义:面积是图形所占平面的大小可知,图A的面积是4个小方格的面积和,即4平方厘米。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)根据长方形的面积=长×宽,以及6×2=12,可知面积是12平方厘米的长方形,可以是长6厘米宽2厘米。
【详解】(1)图A的周长是10厘米,面积是4平方厘米。
(2)(3)
【点睛】作平移后图形时,确定图形的关键点及对应点是解题的关键。画已知面积的长方形时,关键是根据面积公式求出长方形的长与宽。
16.(1)、(3)均见详解
(2)16
【分析】(1)一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;折叠的这条直线叫做这个图形的对称轴,依此补全轴对称图形;
(2)通过平移,将这个图形变成一个长为8厘米,宽为2厘米的长方形(图见详解),长方形的面积=长×宽,依此计算出这个图形的面积即可;
(3)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画图即可。
【详解】(1)、(3)画图如下:
(2)通过平移,如下图所示:
8×2=16(平方厘米)
【点睛】此图考查的是利用平移的方法计算图形的周长,补全轴对称图形,以及作平移后的图形,应熟练掌握。
17.(1)左;6
(2)(3)见详解
(4)12
【分析】(1)从图①中找出一个关键点,再在平移后的图形中找出这个关键点的对应点,观察这两个点之间的位置关系可知,图①向左平移了6格。
(2)图②是某个图形向左平移5格后得到的,则将图②向右平移5格后得到这个图形。
(3)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(4)图④中有9个完整的小方格和6个不完整的小方格,每个不完整的小方格的面积按照完整小方格面积的一半计算,则图④的面积是(9+6÷2)平方厘米。
【详解】(1)图①向左平移了6格。
(2)(3)
(4)9+6÷2
=9+3
=12(平方厘米)
图④的面积是12平方厘米。
【点睛】补全轴对称图形和作平移后图形时,确定图形的关键点及对称点或对应点是解题的关键。用数格子估计不规则图形面积时,注意把不完整格按半格计算,再加上整数格,估算出面积。
18.(1)(2)见详解;(3)10
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)观察这个轴对称图形可知,图形里面有8个完整的小方格,和4个不完整的小方格,每个不完整的小方格按照半个方格的面积计算,则轴对称图形的面积是(8+4÷2)。
【详解】(1)(2)
(3)8+4÷2
=8+2
=10()
则这个轴对称图形的面积是10。
【点睛】补全轴对称图形和作平移后图形时,确定图形的关键点及对称点或对应点是解决本题的关键。求不规则图形面积时,分别数出完整格数和不完整格数,把不完整格按半格计算,再加上整数格,即可求出图形的面积。
19.见详解
【分析】依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行解答。
【详解】
(1)条对称轴 (5)条对称轴
(2)条对称轴 (2)条对称轴
(1)条对称轴 (6)条对称轴
【点睛】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
20.
【分析】涂色部分的大正方形面积是,所以大正方形的边长是;涂色部分的小正方形的面积是,所以小正方形的边长是。题图中的空白部分与小正方形合起来就是一个长为、宽为的长方形,用这个长方形的面积减去小正方形的面积即为空白部分的面积。
【详解】49=7×7
9=3×3
7×3-9
=21-9
=12(m2)
答:空白部分的面积是。
【点睛】熟练掌握正方形和长方形的面积公式是解答本题的关键。
21.;
【分析】题图中的两条小路经过平移后就是一个长为、宽为的长方形,然后利用长方形的面积公式求出两条小路的总面积,再乘30就是一共需要的鹅卵石质量。
【详解】
答:这两条小路的总面积是,大约共需鹅卵石。
【点睛】两条小路的面积和与长20m、宽4m的长方形面积相等,这是解答本题的关键。
22.
【分析】把题图中的小路分别平移到公园的边沿,水平方向的向上平移,竖直方向的向左平移,这样绿地就变成了一个长方形,其中长是,宽是。再根据长方形的面积=长×宽,求出绿地的面积。
【详解】
答:绿地的面积是。
【点睛】本题考查利用平移求图形的面积,通过平移将求不规则图形的面积转换为求规则图形的面积,再根据长方形的面积公式解答即可。
23.377 m2
【详解】(30-1)×(14-1)=377(m2)
答:草坪的面积是377 m2。
24.(1)见详解
(2)长方;15;15
【分析】(1)平移三角形时平移ABC三个点,然后再连接即可,根据要求涂色即可。
(2)根据(1)中得到的图形判断平行后的图形,并根据对应公式计算面积,平移是改变位置,但不改变大小,所以平移前后面积不变。
【详解】(1)如图:
(2)平移后的三角形与四边形ABEF拼成了一个长方形,
长方形的面积=长×宽=3×5=15(cm2),所以平行四边形的面积也是15cm2。
【点睛】本题考查图形的平移及长方形的面积。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
