人教版五年级下册数学数学第七单元折线统计图解答题训练(含答案)
文档属性
| 名称 | 人教版五年级下册数学数学第七单元折线统计图解答题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版五年级下册数学数学第七单元 折线统计图解答题训练
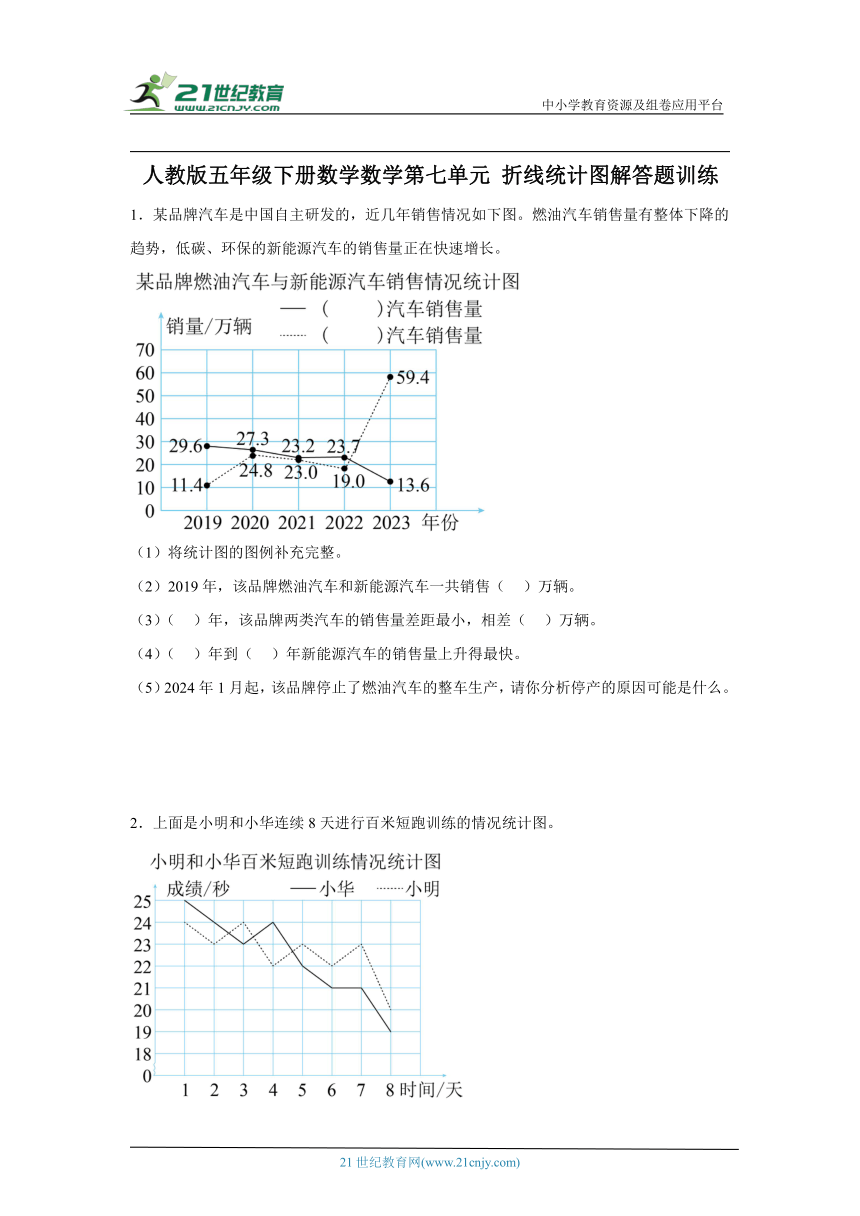
1.某品牌汽车是中国自主研发的,近几年销售情况如下图。燃油汽车销售量有整体下降的趋势,低碳、环保的新能源汽车的销售量正在快速增长。
(1)将统计图的图例补充完整。
(2)2019年,该品牌燃油汽车和新能源汽车一共销售( )万辆。
(3)( )年,该品牌两类汽车的销售量差距最小,相差( )万辆。
(4)( )年到( )年新能源汽车的销售量上升得最快。
(5)2024年1月起,该品牌停止了燃油汽车的整车生产,请你分析停产的原因可能是什么。
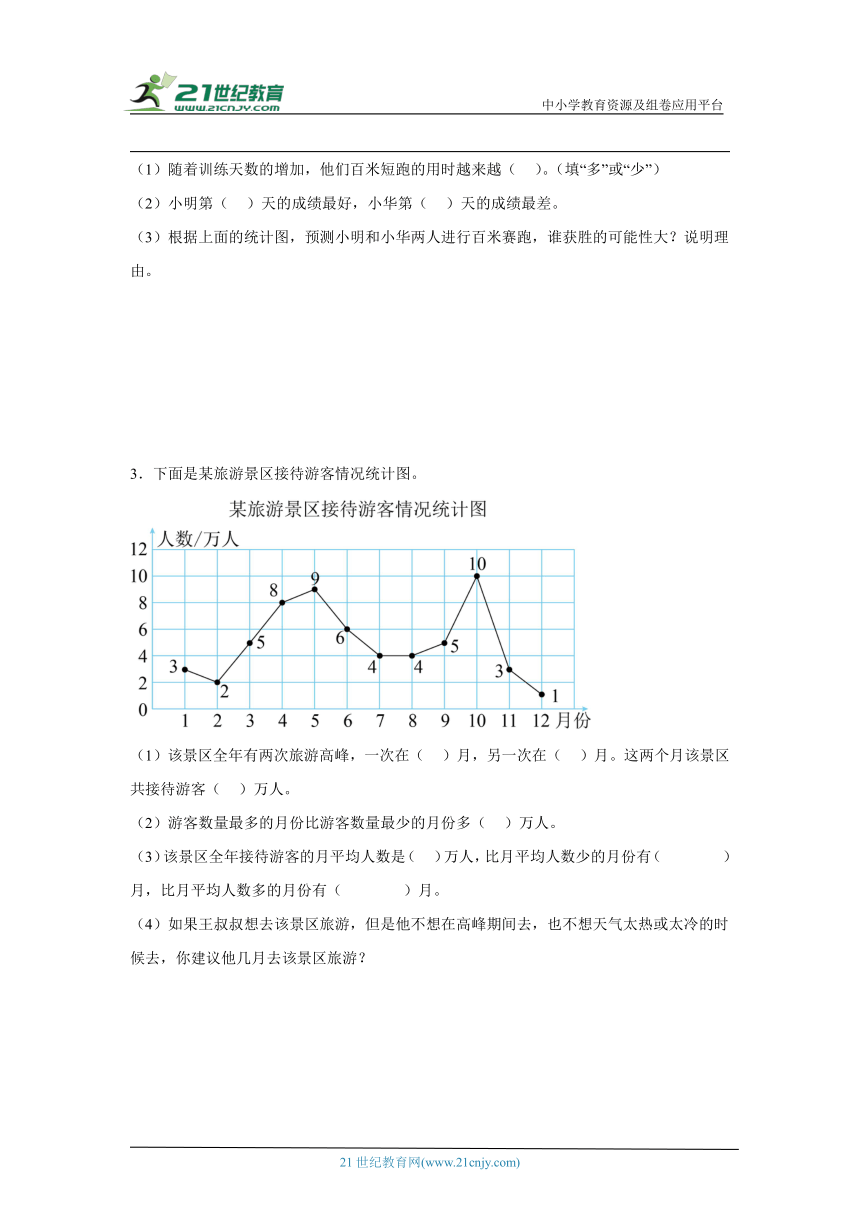
2.上面是小明和小华连续8天进行百米短跑训练的情况统计图。
(1)随着训练天数的增加,他们百米短跑的用时越来越( )。(填“多”或“少”)
(2)小明第( )天的成绩最好,小华第( )天的成绩最差。
(3)根据上面的统计图,预测小明和小华两人进行百米赛跑,谁获胜的可能性大?说明理由。
3.下面是某旅游景区接待游客情况统计图。
(1)该景区全年有两次旅游高峰,一次在( )月,另一次在( )月。这两个月该景区共接待游客( )万人。
(2)游客数量最多的月份比游客数量最少的月份多( )万人。
(3)该景区全年接待游客的月平均人数是( )万人,比月平均人数少的月份有( )月,比月平均人数多的月份有( )月。
(4)如果王叔叔想去该景区旅游,但是他不想在高峰期间去,也不想天气太热或太冷的时候去,你建议他几月去该景区旅游?
4.下面是一辆汽车和一列火车的行程统计图,根据统计图回答问题。
(1)看图填空:
①火车中途停站时间是( )小时。
②汽车比火车早到( )分钟。
(2)汽车的速度是每分钟多少千米?
5.下表是小东0~10岁的身高情况,根据表中的数据绘制折线统计图。
年龄 0 1 2 3 4 5 6 7 8 9 10
身高/厘米 50 76 88 97 104 111 118 124 130 135 141
(1)小东哪一年长得最快?这一年长高了多少厘米?
(2)收集、整理你自己的身高数据,利用方格纸绘制折线统计图,说一说你发现了什么。
6.近日,我市宝峰小学在第三届全国青少年科技教育成果展示大赛中获得“无人机综合应用接力挑战赛”四川省一等奖并成功晋级全国总决赛。下面是该校的A、B两架无人机在一次比赛中飞行时间和高度的记录。
(1)观察上图,我发现( )无人机飞行的时间更长一些,两架无人机的飞行时间相差( )秒。
(2)起飞后第10秒时,A无人机的飞行高度是( )米;起飞后第( )秒时,两架无人机处于同一高度,第25秒时,A无人机飞行高度是B无人机飞行高度的。
(3)我认为( )无人机的飞行情况更好些,理由是:( )。
(4)无人机小组的8名同学在周末有紧急训练任务,老师要尽快打电话通知到每名同学,每次通话需要1分钟,最少需要( )分钟。
7.甲、乙两名大学生去距学校36千米的某乡镇进行社会调查。他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回。乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲。在距乡镇13.5千米处追上甲后同车前往乡镇。已知乙电动车的速度始终不变。结合图象解答下列问题:
(1)电动车的速度为( )千米/分。
(2)甲步行所用的时间为( )分。
(3)求乙返回到学校时,甲与学校相距多远。
8.为了做好第14届全运会的志愿者工作,小明在某周末上午9时骑自行车离开家去北陵公园锻炼,15时回到家。已知自行车离开家的距离s(千米)与时间t(时)之间的关系如图所示,根据图象回答下列问题:
(1)小明骑自行车离家最远的距离是( )千米。
(2)小明骑自行车行驶过程中,最快的车速是( )千米/时,最慢的车速是( )千米/时。
(3)去的途中小明休息了( )次,共休息了( )小时。
(4)小明由离家最远的地方返回家时的平均速度是多少?
9.下面是五(1)班小红、小亮同学一分钟跳绳成绩情况统计图。
(1)每班要派一名同学参加一分钟单人跳绳比赛,你认为派( )去比较合适?原因是什么?
(2)从图中你还能得到哪些信息?(写出两条)
10.下面是红旗商场某月电视和空调的销售情况统计图,看图回答问题。
(1)红旗商场第( )周电视销售量最少,第( )周空调销售量最多。
(2)整体来看,本月空调销售量呈( )趋势,共销售空调( )台。
(3)这个月电视的总销售量比空调的总销售量多( )台。
(4)你还能提出什么数学问题并解答。
11.下面是某服装店去年下半年毛衣和衬衫销售量统计图,看图回答下列问题。
某服装店去年下半年毛衣和衬衫销售量统计图
(1)上图为( )统计图。
(2)毛衣的销售量在( )月最大,衬衫的销售量在( )月最大。
(3)简要分析毛衣和衬衫的销售量的变化情况。
12.2023年6月6日是第28个全国“爱眼日”,主题是“关注普遍的眼健康”。
下面是某小学一至六年级男、女生近视人数统计表。
年级 一 二 三 四 五 六
男生 4 8 10 15 18 24
女生 2 6 14 18 22 26
(1)根据统计表中的信息,请将折线统计图补充完整。
(2)一至六年级男、女生近视的人数是怎样变化的?
(3)五年级男生近视人数是女生近视人数的( )(填最简分数)。
(4)根据图表,你有什么想法或建议?
13.硕硕每年生日时都测量体重,下面是他6-11岁之间测量的体重与同龄男孩标准体重对比的统计图。
(1)从图中可以看出,硕硕的体重在( )岁时最接近标准体重;在( )岁时与标准体重相差最大。在( )岁时比上一年增长的幅度最大。
(2)根据图中提供的信息,请你给硕硕提一些建议。
14.下图是某超市甲、乙两种饮料1-4月份销售情况统计图。
(1)( )月份两种饮料销量相差最大,相差( )件。
(2)根据图中信息,请你提出一个数学问题并解答。
(3)结合甲、乙两种饮料的销售情况,请你给超市经理一个建议,并说说理由。
15.绘图并回答问题。
五(1)班选拔一名女同学参加学校运动会的1分钟仰卧起坐比赛,王芳和李红在比赛前8天进行强化训练,她们每天训练成绩如下表:
时间(第几天) 1 2 3 4 5 6 7 8
王芳的成绩/次 23 30 32 36 38 40 42 44
李红的成绩/次 26 28 34 36 40 34 36 40
(1)请根据统计表完成下面的折线统计图
(2)你认为派谁去参加比赛?为什么?
16.某商城 2023年1-6月销售A、B两种品牌手机,其销量(单位:部)如下统计表:
1月 2月 3月 4月 5月 6月
A 75 80 65 45 50 42
B 30 40 35 48 55 60
(1)根据表中的数据,制成折线统计图。
(2)哪种品牌手机在这6个月中总销售量较好?
(3)从销售情况来看,A、B两种品牌手机的销售情况呈现怎样的变化趋势?
17.下面是某超市2023年电视销售情况统计图,其中A品牌电视机第一季度销售2850台,第三季度销售3000台,请结合统计图回答问题。
(1)A品牌电视机第二季度的销售数量比B品牌四个季度的平均销售数量多50台,A品牌电视机在第二季度销售了( )台。
(2)A品牌电视机第四季度的销售数量与第三季度的销售数量持平,请你将上面的折线统计图画完整。
(3)在第三季度中,B品牌电视机的销售数量相当于A品牌的。
18.根据洋洋本学期六次考试成绩情况解决问题。
一 二 三 四 五 六
语文 85 83 87 86 89 88
数学 90 85 80 92 80 95
(1)请根据表中的数据画出折线统计图。
(2)数学最高分比最低分高( )分,语文最高分比最低分高( )分。
(3)请你给洋洋以后的学习提一点合理的建议。
19.下面是希望小学五年级喜欢打篮球和踢足球的人数统计表。
(1)根据上面统计表中的数据画出折线统计图。
(2)希望小学五年级学生喜欢( )的人数多,比喜欢打篮球的多( )人。
(3)请你提出一个数学问题并解答。
20.下面是某市五月某一天部分时刻气温统计表。
时刻 7:00 9:00 11:00 13:00 15:00 17:00 19:00
气温/℃ 12 15 22 24 23 18 8
(1)根据统计表绘制折线统计图。
(2)( )的气温最高,最高与最低气温相差了( )℃。
(3)该日7:00至13:00的气温变化趋势是( )。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)燃油;新能源
(2)41
(3)2021;0.2
(4)2022;2023
(5)见详解
【分析】(1)根据题意,燃油汽车销售量有整体下降的趋势,新能源汽车的销售量正在快速增长,得出复式折线统计图中的实线表示燃油汽车销售量,虚线表示新能源汽车销售量;据此将统计图的图例补充完整。
(2)从图中可知,2019年燃油汽车、新能源汽车分别销售11.4万辆、29.6万辆,再相加即是这一年两种汽车的销售总量。
(3)观察复式折线统计图中的两条折线,折线叉口越小,说明这一年两种汽车销售量差距越小,然后相减,求出两种汽车销售量的差值。
(4)观察表示新能源汽车销售量的折线变化趋势,折线越陡,表示销售量上升越快。
(5)结合复式折线统计图提供的信息,分析停止生产燃油汽车的原因,合理即可。
【详解】
(1)如图:
(2)11.4+29.6=41(万辆)
2019年,该品牌燃油汽车和新能源汽车一共销售41万辆。
(3)23.2-23=0.2(万辆)
2021年,该品牌两类汽车的销售量差距最小,相差0.2万辆。
(4)2022年到2023年新能源汽车的销售量上升得最快。
(5)我分析停产的原因可能是燃油汽车销售量呈下降趋势。(答案不唯一)
2.(1)少
(2)8;1
(3)小华;见详解
【分析】
(1)观察复式折线统计图可知,两人的折线呈下降趋势,即百米短跑的用时越来越少。
(2)百米短跑用时越少,成绩越好;据此从表示小明训练情况的折线中找到最低点,说明这一天小明的成绩最好;从表示小华训练情况的折线中找到最高点,说明这一天小华的成绩最差。
(3)根据统计图提供的信息,预测两人进行百米赛跑,谁获胜的可能性大,理由合理即可。
【详解】(1)随着训练天数的增加,他们百米短跑的用时越来越少。
(2)小明第8天的成绩最好,小华第1天的成绩最差。
(3)小华获胜的可能性大,因为小华比小明进步得快,且第8天的成绩比小明好。(答案不唯一)
3.(1)5;10;19
(2)9
(3)5;1、2、7、8、11、12;4、5、6、10
(4)见详解
【分析】
(1)观察折线统计图,折线的较高的两个点表示接待游客人数较多,找到对应的月份即是该景区全年的两次旅游高峰,将这两个月接待的游客人数相加即可。
(2)从图中可知,游客数量最多的月份是10月份,有10万人;游客数量最少的月份是12月份,有1万人;用减法求出10月份比12月份多的人数即可。
(3)先把每月景区接待游客人数相加,求出总人数,再除以12,即是平均每月接待游客的人数;结合统计图中的数据,找出比月平均人数少的月份和多的月份。
(4)王叔叔不想在高峰期间去,排除5月和10月;也不想天气太热或太冷的时候去,可以排除1月、2月、6月、7月、8月、11月、12月,据此给出建议,合理即可。
【详解】(1)9+10=19(万人)
该景区全年有两次旅游高峰,一次在5月,另一次在10月。这两个月该景区共接待游客19万人。
(2)10-1=9(万人)
游客数量最多的月份比游客数量最少的月份多9万人。
(3)(3+2+5+8+9+6+4+4+5+10+3+1)÷12
=60÷12
=5(万人)
该景区全年接待游客的月平均人数是5万人,比月平均人数少的月份有1、2,7、8、11、12月,比月平均人数多的月份有4、5、6、10月。
(4)我建议他3月或9月去该景区旅游。(答案不唯一)
4.(1)①;②5
(2)0.6千米
【分析】(1)①从图中可知,8:00~8:10这段时间火车没有行驶,由此可知火车中途停站10分钟,再根据进率“1小时=60分”换算单位。
②从图中可知,汽车是8:20到站,火车是8:25到站,用火车到站时刻减去汽车到站时刻,即可求出汽车比火车早到多少分钟。
(2)从图中可知,汽车是7:55出发,8:20到站,共行驶15千米;先用到站时刻减去出发时刻,求出汽车行驶的时间;再根据“速度=路程÷时间”,求出汽车的速度。
【详解】(1)看图填空:
①8时10分-8时=10(分钟)
10÷60=(小时)
火车中途停站时间是小时。
②8时25分-8时20分=5(分钟)
汽车比火车早到5分钟。
(2)8时20分-7时55分=25(分钟)
15÷25=0.6(千米)
答:汽车的速度是每分钟0.6千米。
5.图见详解
(1)0~1岁;26厘米
(2)图见详解;发现:我在0~1岁这一年长得最快
【分析】根据统计表中的数据,先描点,再连线,画出相应的折线统计图。
(1)根据折线统计图可知,小东0~1岁这一年长得最快,用1岁的身高减去0岁的,求出长高了多少厘米;
(2)根据自己的身高数据,先整理出自己0~10岁的身高情况,然后画出折线统计图,并从中获得信息,分析解答即可。
【详解】
(1)76-50=26(厘米)
答:小东0~1岁这一年长得最快,这一年长高了26厘米。
(2)我的0~10岁身高情况统计表:
年龄 0 1 2 3 4 5 6 7 8 9 10
身高/厘米 50 75 85 98 110 117 125 132 142 148 150
答:我发现我在0~1岁这一年长得最快。
(答案不唯一)
6.(1)B;5
(2)20;15;
(3)B;B无人机的飞行时间更长、从整体看,B无人机飞得更高
(4)8
【分析】(1)观察复试折线统计图,横轴表示飞行时间,纵轴表示飞行高度。观察A、B两架无人机飞行时间分别是35秒和40秒,求出两者之差即可。
(2)观察A的折线统计图第10秒在20米的高度,两条折线相交的点在纵轴的位置就是同一高度。分别找到A在25秒是高度20米,B在25秒时高度是25米,用20÷25即可。
(3)观察飞行时间和飞行高度,飞行时间越长,高度越高的飞行情况就好些,据此解答。
(4)老师首先用1分钟通知第一个学生;1+1=2,第二分钟由老师和1个学生两人分别通知1个学生,现在通知的一共2+2-1=3个学生;第三分钟可以推出通知的一共4+4-1=7个学生;还有1名同学,第四分钟通知,由此问题解决。
【详解】(1)A无人机飞行时间是35秒,B无人机飞行时间是40秒。
35<40,40-35=5(秒)
即,观察上图,我发现B无人机飞行的时间更长一些,两架无人机的飞行时间相差5秒。
(2)A无人机第10秒在20米的高度,起飞后第15秒两架无人机在同一高度。
20÷25==
即,起飞后第10秒时,A无人机的飞行高度是20米,起飞后第15秒时,两架无人机处于同一高度,第25秒时,A无人机飞行高度是B无人机飞行高度的。
(3)我认为B无人机的飞行情况更好些,理由是;B无人机的飞行时间更长、从整体看,B无人机飞得更高。
(4)第一分钟通知到1名同学;
第二分钟最多可通知到3名同学;
第三分钟最多可通知到7名同学;
第四分钟时可以通知到第8名同学。即,最少需要4分钟。
7.(1)0.9;
(2)45;
(3)20千米
【分析】(1)由折线统计图可知:甲、乙两名大学生骑电动车20分钟走了18千米,根据路程÷时间=速度,用18÷20可求出电动车的速度是0.9千米/分。
(2)由题意可知:甲步行所用的时间等于乙骑电动车行驶(36-13.5+18)千米的时间。根据路程÷速度=时间,用(36-13.5+18)÷0.9可求出甲步行所用的时间是45分钟。
(3)由题意可知:甲步行45分钟所走的路程是36-13.5-18=4.5(千米),根据路程÷时间=速度,用4.5÷45可求出甲步行的速度是0.1千米/分;乙返回到学校用了20分钟,根据速度×时间=路程,用0.1×20可求出甲20分钟所走的路程是2千米;最后用2千米加上甲、乙骑电动车所走的18千米可求出甲与学校相距的千米数。
【详解】(1)18÷20=0.9(千米/分)
所以,电动车的速度为0.9千米/分。
(2)(36-13.5+18)÷0.9
=(22.5+18)÷0.9
=40.5÷0.9
=45(分)
所以,甲步行所用的时间为45分。
(3)(36-13.5-18)÷45
=4.5÷45
=0.1(千米/分)
0.1×20+18
=2+18
=20(千米)
答:甲与学校相距20千米远。
8.(1)35
(2)20;10
(3)1;0.5
(4)17.5千米/时
【分析】(1)观察图象可知,小明骑自行车离家最远的距离对应的是最上面的一段,即在12时~13时,距离为35千米。
(2)观察图象可知,小明骑自行车行驶过程中,行驶最快时对应的线段最陡,行驶最慢时对应的线段最平缓;
即小明在10时~10.5时对应的速度最快,在11时~12时的速度最慢;根据“速度=路程÷时间”,分别求出最快的车速度和最慢的车速。
(3)在10.5时~11时,线段水平,表示这段时间的路程不变,此时小明在休息,据此解答。
(4)小明离家最远的地方是35千米,返回家一共用时(15-13)时,根据“速度=路程÷时间”,即可求出返回家时的平均速度。
【详解】(1)小明骑自行车离家最远的距离是35千米。
(2)小明在10时~10.5时骑车速度最快:
(25-15)÷(10.5-10)
=10÷0.5
=20(千米/时)
在11时~12时骑车速度最慢:
(35-25)÷(12-11)
=10÷1
=10(千米/时)
小明骑自行车行驶过程中,最快的车速是20千米/时,最慢的车速是10千米/时。
(3)11-10.5=0.5(小时)
去的途中小明休息了1次,共休息了0.5小时。
(4)35÷(15-13)
=35÷2
=17.5(千米/时)
答:小明由离家最远的地方返回家时的平均速度是17.5千米/时。
【点睛】结合距离和时间的关系图象,考查对不同时间段运动状态的分析,并根据速度、时间、路程之间的关系解答。
9.(1)小红;见详解
(2)见详解
【分析】(1)观察复式折线统计图中两条折线的变化趋势,得出小红的跳绳成绩更好、更稳定。
(2)从统计图中获取信息,写出两条有关的信息,合理即可。
【详解】(1)我认为派小红去比较合适。
因为从统计图中可以看出,第5次~第10次小红跳绳个数基本呈递增趋势,而小亮跳绳个数时增时减,所以应该派小红参加比赛。(原因不唯一)
(2)从图中还能得到以下信息:
①小红一分钟跳绳成绩最好是167下,小亮一分钟跳绳成绩最好是165下。
②小红和小亮第6次的跳绳成绩相差5下。
(答案不唯一)
【点睛】理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(1)二;四;(2)上升;157;(3)96;(4)本月第一周电视销售量比空调销售量多多少台?36台
【分析】(1)实线表示电视销售量,虚线表示空调销售量,观察实线的最低点在哪一周,则对应的一周电视销售量最少;观察虚线的最高点在哪一周,则对应的一周空调销售量最多;
(2)观察虚线的走向,发现本月空调销售量呈上升趋势,根据加法的意义,用22+35+44+56即可求出这个月的空调总销售量;
(3)根据加法的意义,用58+53+64+78即可求出这个月电视的总销售量;然后用这个月电视的总销售量减去空调的总销售量,即可求出这个月电视的总销售量比空调的总销售量多多少台;
(4)提出的问题合理即可,例如:本月第一周电视销售量比空调销售量多多少台。
【详解】(1)观察统计图可知,红旗商场第二周电视销售量最少,第四周空调销售量最多。
(2)22+35+44+56=157(台)
根据分析可知,本月空调销售量呈上升趋势,共销售空调157台。
(3)58+53+64+78=253(台)
253-157=96(台)
这个月电视的总销售量比空调的总销售量多96台。
(4)问题:本月第一周电视销售量比空调销售量多多少台?
58-22=36(台)
答:本月第一周电视销售量比空调销售量多36台。(答案不唯一)
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)复式折线
(2)十一;七
(3)下半年毛衣销售量呈上升趋势,下半年衬衫销售量呈下降趋势。
【分析】(1)根据统计图的特点可知,这个图是复式折线统计图;
(2)代表毛衣和衬衫的折线上的最高点表示销售量最大;
(3) 折线向上表示呈上升趋势,折线向下表示呈下降趋势。(答案不唯一)
【详解】(1)上图为复式折线统计图。
(2)毛衣的销售量在十一月最大,衬衫的销售量在七月最大。
(3)下半年毛衣销售量呈上升趋势,下半年衬衫销售量呈下降趋势。
【点睛】本题考查复式折线统计图,通过统计图分析出相应的数据是解题的关键。
12.(1)见详解;
(2)随着年级的升高,男、女生近视的人数逐渐增多;(答案不唯一)
(3);
(4)见详解
【分析】(1)统计图中横轴表示年级,纵轴表示人数,单位长度表示2人,根据表格中的数据描出表示女生近视人数的各点,再用实线依次连接各点,最后在各点处标出对应的数据;
(2)如果折线统计图中的折线呈上升趋势,那么近视人数增多;如果折线统计图中的折线呈下降趋势,那么近视人数减少;
(3)五年级男生近视人数有18人,女生近视人数有22人,A是B的几分之几的计算方法:A÷B=,结果化为最简分数;
(4)一至六年级男、女生近视的人数越来越多,同学们应多做眼保健操、注意用眼卫生、保护视力,言之有理即可。
【详解】(1)分析可知:
(2)观察复式折线统计图可知,随着年级的升高,男、女生近视的人数逐渐增多。(答案不唯一)
(3)18÷22=
所以,五年级男生近视人数是女生近视人数的。
(4)同学们平时应注意用眼卫生,多做眼保健操,减少看电子产品的时间,保护视力。(答案不唯一)
【点睛】掌握折线统计图的特点及作用和一个数占另一个数几分之几的计算方法是解答题目的关键。
13.(1)6;10;9;(2)见详解;(答案不唯一)
【分析】(1)利用减法分别计算6-11岁之间测量硕硕的体重与同龄男孩标准体重之间的差值,比较6-11岁之间差值的大小,即可求出硕硕的体重在几岁时最接近标准体重以及在几岁时与标准体重相差最大。依次用硕硕7岁时体重减去6岁时的体重,8岁时体重减去7岁时的体重,9岁时体重减去8岁时的体重,10岁时体重减去9岁时的体重,11岁时体重减去10岁时的体重,求出当前岁数比上一年增长的体重,比较每一年增长体重的大小,即可求出在几岁时比上一年增长的幅度最大。
(2)观察统计图,实线数据整体高于虚线数据,表示硕硕的体重高于标准体重,建议合理即可。
【详解】(1)24-21=3(千克)
28-22=6(千克)
31-23=8(千克)
36-26=10(千克)
40-28=12(千克)
42-31=11(千克)
3<6<8<10<11<12
即硕硕的体重在6岁时最接近标准体重;在10岁时与标准体重相差最大。
28-24=4(千克)
31-28=3(千克)
36-31=5(千克)
40-36=4(千克)
42-40=2(千克)
2<3<4<5
即在9岁时比上一年增长的幅度最大。
(2)答:我给硕硕的建议是少吃高脂肪含量的食品,多多运动。(答案不唯一,合理即可)
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)4;43;
(2)3月份甲种饮料的销量占乙种饮料销量的几分之几?;(答案不唯一)
(3)见详解
【分析】(1)复式折线统计图中,横轴表示月份,纵轴表示销量,单位长度表示25件,两条折线之间的距离越大,两种饮料销量相差越大,两条折线之间的距离越小,两种饮料销量相差越小;
(2)3月份甲种饮料的销量占乙种饮料销量的几分之几?A是B的几分之几的计算方法:A÷B=,结果化为最简分数;
(3)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,根据两种饮料销量的变化趋势分析问题,据此解答。
【详解】(1)4月份两点的距离最大。
96-53=43(件)
由复式折线统计图可知,4月份两种饮料销量相差最大,相差43件。
(2)数学问题:3月份甲种饮料的销量占乙种饮料销量的几分之几?
56÷70=
答:3月份甲种饮料的销量占乙种饮料销量的。(答案不唯一)
(3)观察复式折线统计图可知,甲种饮料的销量呈逐渐上升的趋势,乙种饮料的销量1月-2月,3月-4月呈下降趋势,2月-3月呈上升趋势,甲种饮料越来越畅销,建议超市经理进货时多进甲种饮料,少进乙种饮料。(答案不唯一)
【点睛】掌握折线统计图的特点及作用和一个数占另一个数几分之几的计算方法是解答题目的关键。
15.(1)见详解;(2)王芳;王芳的成绩比较好
【分析】(1)根据表格的数据在统计图上描出各点,再依次连接即可,实线表示王芳的数据,虚线表示李红的数据;
(2)观察统计图可知,王芳的成绩稳步上升,李红的成绩不稳定,所以派王芳去参加比赛比较合适。
【详解】(1)如图:
(2)派王芳去参加比赛比较合适,因为王芳的成绩比较好。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
16.(1)见详解;(2)A品牌;(3)见详解
【分析】(1)折线统计图的绘制方法是:先整理数据;利用纵轴和横轴上的长度单位所表示的数量,根据数量的多少描出各点,再把各点用线段顺次连接起来。
(2)观察折线统计图,实线代表A手机的销售情况,虚线代表B手机的销售情况,从两条折线的总体情况来看,在这6个月中A手机比B手机的总体情况要好一些。
(3)在1-2月A品牌的手机销量是往上增长,从2月开始,呈下降的趋势;B品牌的手机销量在前3个月起起伏伏,从3月开始,呈上升的趋势。
【详解】(1)如图:
(2)答:A品牌手机在这6个月中总销售量较好。
(3)答:从销售情况来看,A品牌手机的销售情况呈下降的趋势,B品牌手机的销售情况呈上升的趋势。
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)2800
(2)见详解
(3)
【分析】(1)根据:平均数=总数÷份数,求出B品牌四个季度的平均销售数量,再加上50台即可计算出A品牌电视机在第二季度销售台数;
(2)A品牌电视机第四季度的销售数量与第三季度的销售数量持平,第三季度是3000台,那么第四季度也是3000台,再根据(1)中A品牌电视机在第二季度的销售数量,补充折线即可;
(3)求第三季度中,B品牌电视机的销售数量相当于A品牌的几分之几,用B品牌电视机第三季度的销售数量除以A品牌第三季度的销售数量,结果用分数表示即可。
【详解】(1)(2400+2700+2800+3100)÷4
=(5100+2800+3100)÷4
=11000÷4
=2750(台)
2750+50=2800(台)
所以,A品牌电视机在第二季度销售了(2800)台。
(2)作图如下:
(3)2800÷3000=
所以,在第三季度中,B品牌电视机的销售数量相当于A品牌的。
【点睛】此题考查了折线统计图、平均数以及分数与除法的关系,关键能够从统计图获取正确信息再解答。
18.(1)见详解;
(2)15;6
(3)数学成绩不稳定波动较大,需要多加练习(答案不唯一)
【分析】(1)统计图中横轴表示次数,纵轴表示成绩,单位长度表示2分,根据表格中的数据画出表示语文和数学每次的分数,再用实线依次连接表示语文分数的各点,用虚线依次连接表示数学分数的各点,最后标出对应的数据;
(2)折线统计图中折点越高对应的分数越高,折点越低对应的分数越低,分别找出数学和语文的最高分和最低分,再求出它们的差;
(3)复式折线统计图中表示数学成绩的折线波动较大,成绩不稳定,表示语文成绩的折线波动较小,成绩稳定,应多做习题巩固知识,数学成绩稳步提升,据此解答。
【详解】(1)分析可知:
(2)由复式折线统计图可知,数学最高分为95分,最低分为80分,语文最高分为89分,最低分为83分。
95-80=15(分)
89-83=6(分)
所以,数学最高分比最低分高15分,语文最高分比最低分高6分。
(3)观察复式折线统计图可知,洋洋的数学成绩不稳定波动较大,需要多加练习。(答案不唯一)
【点睛】本题主要考查统计图表的综合应用,掌握折线统计图的特点及作用是解答题目的关键。
19.(1)见详解;(2)踢足球;6;(3)五年级喜欢打篮球和踢足球的人数一共有多少人?;168人
【分析】(1)根据表格数据绘制折现统计图即可;(2)分别计算出五年级喜欢打篮球和喜欢踢足球的总人数,再进行比较即可得出结论;(3)根据表格数据可计算出五年级喜欢打篮球和踢足球的总人数,本小题的答案并不唯一,符合题意即可。
【详解】(1)折线统计图如下:
(2)喜欢打篮球:13+16+8+17+12+15=81(人)
喜欢踢足球:18+11+14+16+9+19=87(人)
87-81=6(人)
因此希望小学五年级学生喜欢踢足球的人数多,比喜欢打篮球的多6人。
(3)可提的数学问题:五年级喜欢打篮球和踢足球的人数一共有多少人?
13+16+8+17+12+15+18+11+14+16+9+19=168(人)
答:五年级喜欢打篮球和踢足球的人数一共有168人。
【点睛】解答本题的关键是抓住图表信息,结合问题进行分析即可完成解答。
20.(1)见详解。
(2)13:00;16
(3)上升
【分析】(1)横轴表示时刻,纵轴表示气温,一个单位长度表示2℃。先根据统计表中的数据,在横上找到相应时刻的点,在纵轴上找到该时刻所对应的气温的点,过两点分别过横轴、纵轴的垂线,两条垂线的交点就是所要描的点,在交点处点上实心点;将所有的实心点用线段顺次连接起来,并在所描点的上方或下方标上数据。
(2)先找到折线统计图上的最高点,再过最高点作横轴的垂线,垂足处的时刻即是气温最高时的时刻;用折线统计图上最高点对应的气温减去最低点对应的气温,即可求出最高与最低气温的温差。
(3)观察折线统计图发现:表示该日7:00至13:00的折线呈上升趋势,即该日7:00至13:00的气温变化趋势是上升趋势。
【详解】(1)如下图:
(2)折线上最高点所对应的时刻是13:00,最高点所对应的气温是24℃,最低点所对应的气温是8℃,24-8=16(℃),所以13:00的气温最高,最高与最低气温相差了16℃。
(3)通过观察折线统计图可知,该日7:00至13:00的气温变化趋势是上升。
【点睛】运用横向、纵向、综合、对比等不同的观察方法,可以读懂折线统计图,从中获取更多的信息,并能根据信息回答或提出相应的问题,同时进行简单的分析和合理的预测。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版五年级下册数学数学第七单元 折线统计图解答题训练
1.某品牌汽车是中国自主研发的,近几年销售情况如下图。燃油汽车销售量有整体下降的趋势,低碳、环保的新能源汽车的销售量正在快速增长。
(1)将统计图的图例补充完整。
(2)2019年,该品牌燃油汽车和新能源汽车一共销售( )万辆。
(3)( )年,该品牌两类汽车的销售量差距最小,相差( )万辆。
(4)( )年到( )年新能源汽车的销售量上升得最快。
(5)2024年1月起,该品牌停止了燃油汽车的整车生产,请你分析停产的原因可能是什么。
2.上面是小明和小华连续8天进行百米短跑训练的情况统计图。
(1)随着训练天数的增加,他们百米短跑的用时越来越( )。(填“多”或“少”)
(2)小明第( )天的成绩最好,小华第( )天的成绩最差。
(3)根据上面的统计图,预测小明和小华两人进行百米赛跑,谁获胜的可能性大?说明理由。
3.下面是某旅游景区接待游客情况统计图。
(1)该景区全年有两次旅游高峰,一次在( )月,另一次在( )月。这两个月该景区共接待游客( )万人。
(2)游客数量最多的月份比游客数量最少的月份多( )万人。
(3)该景区全年接待游客的月平均人数是( )万人,比月平均人数少的月份有( )月,比月平均人数多的月份有( )月。
(4)如果王叔叔想去该景区旅游,但是他不想在高峰期间去,也不想天气太热或太冷的时候去,你建议他几月去该景区旅游?
4.下面是一辆汽车和一列火车的行程统计图,根据统计图回答问题。
(1)看图填空:
①火车中途停站时间是( )小时。
②汽车比火车早到( )分钟。
(2)汽车的速度是每分钟多少千米?
5.下表是小东0~10岁的身高情况,根据表中的数据绘制折线统计图。
年龄 0 1 2 3 4 5 6 7 8 9 10
身高/厘米 50 76 88 97 104 111 118 124 130 135 141
(1)小东哪一年长得最快?这一年长高了多少厘米?
(2)收集、整理你自己的身高数据,利用方格纸绘制折线统计图,说一说你发现了什么。
6.近日,我市宝峰小学在第三届全国青少年科技教育成果展示大赛中获得“无人机综合应用接力挑战赛”四川省一等奖并成功晋级全国总决赛。下面是该校的A、B两架无人机在一次比赛中飞行时间和高度的记录。
(1)观察上图,我发现( )无人机飞行的时间更长一些,两架无人机的飞行时间相差( )秒。
(2)起飞后第10秒时,A无人机的飞行高度是( )米;起飞后第( )秒时,两架无人机处于同一高度,第25秒时,A无人机飞行高度是B无人机飞行高度的。
(3)我认为( )无人机的飞行情况更好些,理由是:( )。
(4)无人机小组的8名同学在周末有紧急训练任务,老师要尽快打电话通知到每名同学,每次通话需要1分钟,最少需要( )分钟。
7.甲、乙两名大学生去距学校36千米的某乡镇进行社会调查。他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回。乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲。在距乡镇13.5千米处追上甲后同车前往乡镇。已知乙电动车的速度始终不变。结合图象解答下列问题:
(1)电动车的速度为( )千米/分。
(2)甲步行所用的时间为( )分。
(3)求乙返回到学校时,甲与学校相距多远。
8.为了做好第14届全运会的志愿者工作,小明在某周末上午9时骑自行车离开家去北陵公园锻炼,15时回到家。已知自行车离开家的距离s(千米)与时间t(时)之间的关系如图所示,根据图象回答下列问题:
(1)小明骑自行车离家最远的距离是( )千米。
(2)小明骑自行车行驶过程中,最快的车速是( )千米/时,最慢的车速是( )千米/时。
(3)去的途中小明休息了( )次,共休息了( )小时。
(4)小明由离家最远的地方返回家时的平均速度是多少?
9.下面是五(1)班小红、小亮同学一分钟跳绳成绩情况统计图。
(1)每班要派一名同学参加一分钟单人跳绳比赛,你认为派( )去比较合适?原因是什么?
(2)从图中你还能得到哪些信息?(写出两条)
10.下面是红旗商场某月电视和空调的销售情况统计图,看图回答问题。
(1)红旗商场第( )周电视销售量最少,第( )周空调销售量最多。
(2)整体来看,本月空调销售量呈( )趋势,共销售空调( )台。
(3)这个月电视的总销售量比空调的总销售量多( )台。
(4)你还能提出什么数学问题并解答。
11.下面是某服装店去年下半年毛衣和衬衫销售量统计图,看图回答下列问题。
某服装店去年下半年毛衣和衬衫销售量统计图
(1)上图为( )统计图。
(2)毛衣的销售量在( )月最大,衬衫的销售量在( )月最大。
(3)简要分析毛衣和衬衫的销售量的变化情况。
12.2023年6月6日是第28个全国“爱眼日”,主题是“关注普遍的眼健康”。
下面是某小学一至六年级男、女生近视人数统计表。
年级 一 二 三 四 五 六
男生 4 8 10 15 18 24
女生 2 6 14 18 22 26
(1)根据统计表中的信息,请将折线统计图补充完整。
(2)一至六年级男、女生近视的人数是怎样变化的?
(3)五年级男生近视人数是女生近视人数的( )(填最简分数)。
(4)根据图表,你有什么想法或建议?
13.硕硕每年生日时都测量体重,下面是他6-11岁之间测量的体重与同龄男孩标准体重对比的统计图。
(1)从图中可以看出,硕硕的体重在( )岁时最接近标准体重;在( )岁时与标准体重相差最大。在( )岁时比上一年增长的幅度最大。
(2)根据图中提供的信息,请你给硕硕提一些建议。
14.下图是某超市甲、乙两种饮料1-4月份销售情况统计图。
(1)( )月份两种饮料销量相差最大,相差( )件。
(2)根据图中信息,请你提出一个数学问题并解答。
(3)结合甲、乙两种饮料的销售情况,请你给超市经理一个建议,并说说理由。
15.绘图并回答问题。
五(1)班选拔一名女同学参加学校运动会的1分钟仰卧起坐比赛,王芳和李红在比赛前8天进行强化训练,她们每天训练成绩如下表:
时间(第几天) 1 2 3 4 5 6 7 8
王芳的成绩/次 23 30 32 36 38 40 42 44
李红的成绩/次 26 28 34 36 40 34 36 40
(1)请根据统计表完成下面的折线统计图
(2)你认为派谁去参加比赛?为什么?
16.某商城 2023年1-6月销售A、B两种品牌手机,其销量(单位:部)如下统计表:
1月 2月 3月 4月 5月 6月
A 75 80 65 45 50 42
B 30 40 35 48 55 60
(1)根据表中的数据,制成折线统计图。
(2)哪种品牌手机在这6个月中总销售量较好?
(3)从销售情况来看,A、B两种品牌手机的销售情况呈现怎样的变化趋势?
17.下面是某超市2023年电视销售情况统计图,其中A品牌电视机第一季度销售2850台,第三季度销售3000台,请结合统计图回答问题。
(1)A品牌电视机第二季度的销售数量比B品牌四个季度的平均销售数量多50台,A品牌电视机在第二季度销售了( )台。
(2)A品牌电视机第四季度的销售数量与第三季度的销售数量持平,请你将上面的折线统计图画完整。
(3)在第三季度中,B品牌电视机的销售数量相当于A品牌的。
18.根据洋洋本学期六次考试成绩情况解决问题。
一 二 三 四 五 六
语文 85 83 87 86 89 88
数学 90 85 80 92 80 95
(1)请根据表中的数据画出折线统计图。
(2)数学最高分比最低分高( )分,语文最高分比最低分高( )分。
(3)请你给洋洋以后的学习提一点合理的建议。
19.下面是希望小学五年级喜欢打篮球和踢足球的人数统计表。
(1)根据上面统计表中的数据画出折线统计图。
(2)希望小学五年级学生喜欢( )的人数多,比喜欢打篮球的多( )人。
(3)请你提出一个数学问题并解答。
20.下面是某市五月某一天部分时刻气温统计表。
时刻 7:00 9:00 11:00 13:00 15:00 17:00 19:00
气温/℃ 12 15 22 24 23 18 8
(1)根据统计表绘制折线统计图。
(2)( )的气温最高,最高与最低气温相差了( )℃。
(3)该日7:00至13:00的气温变化趋势是( )。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)燃油;新能源
(2)41
(3)2021;0.2
(4)2022;2023
(5)见详解
【分析】(1)根据题意,燃油汽车销售量有整体下降的趋势,新能源汽车的销售量正在快速增长,得出复式折线统计图中的实线表示燃油汽车销售量,虚线表示新能源汽车销售量;据此将统计图的图例补充完整。
(2)从图中可知,2019年燃油汽车、新能源汽车分别销售11.4万辆、29.6万辆,再相加即是这一年两种汽车的销售总量。
(3)观察复式折线统计图中的两条折线,折线叉口越小,说明这一年两种汽车销售量差距越小,然后相减,求出两种汽车销售量的差值。
(4)观察表示新能源汽车销售量的折线变化趋势,折线越陡,表示销售量上升越快。
(5)结合复式折线统计图提供的信息,分析停止生产燃油汽车的原因,合理即可。
【详解】
(1)如图:
(2)11.4+29.6=41(万辆)
2019年,该品牌燃油汽车和新能源汽车一共销售41万辆。
(3)23.2-23=0.2(万辆)
2021年,该品牌两类汽车的销售量差距最小,相差0.2万辆。
(4)2022年到2023年新能源汽车的销售量上升得最快。
(5)我分析停产的原因可能是燃油汽车销售量呈下降趋势。(答案不唯一)
2.(1)少
(2)8;1
(3)小华;见详解
【分析】
(1)观察复式折线统计图可知,两人的折线呈下降趋势,即百米短跑的用时越来越少。
(2)百米短跑用时越少,成绩越好;据此从表示小明训练情况的折线中找到最低点,说明这一天小明的成绩最好;从表示小华训练情况的折线中找到最高点,说明这一天小华的成绩最差。
(3)根据统计图提供的信息,预测两人进行百米赛跑,谁获胜的可能性大,理由合理即可。
【详解】(1)随着训练天数的增加,他们百米短跑的用时越来越少。
(2)小明第8天的成绩最好,小华第1天的成绩最差。
(3)小华获胜的可能性大,因为小华比小明进步得快,且第8天的成绩比小明好。(答案不唯一)
3.(1)5;10;19
(2)9
(3)5;1、2、7、8、11、12;4、5、6、10
(4)见详解
【分析】
(1)观察折线统计图,折线的较高的两个点表示接待游客人数较多,找到对应的月份即是该景区全年的两次旅游高峰,将这两个月接待的游客人数相加即可。
(2)从图中可知,游客数量最多的月份是10月份,有10万人;游客数量最少的月份是12月份,有1万人;用减法求出10月份比12月份多的人数即可。
(3)先把每月景区接待游客人数相加,求出总人数,再除以12,即是平均每月接待游客的人数;结合统计图中的数据,找出比月平均人数少的月份和多的月份。
(4)王叔叔不想在高峰期间去,排除5月和10月;也不想天气太热或太冷的时候去,可以排除1月、2月、6月、7月、8月、11月、12月,据此给出建议,合理即可。
【详解】(1)9+10=19(万人)
该景区全年有两次旅游高峰,一次在5月,另一次在10月。这两个月该景区共接待游客19万人。
(2)10-1=9(万人)
游客数量最多的月份比游客数量最少的月份多9万人。
(3)(3+2+5+8+9+6+4+4+5+10+3+1)÷12
=60÷12
=5(万人)
该景区全年接待游客的月平均人数是5万人,比月平均人数少的月份有1、2,7、8、11、12月,比月平均人数多的月份有4、5、6、10月。
(4)我建议他3月或9月去该景区旅游。(答案不唯一)
4.(1)①;②5
(2)0.6千米
【分析】(1)①从图中可知,8:00~8:10这段时间火车没有行驶,由此可知火车中途停站10分钟,再根据进率“1小时=60分”换算单位。
②从图中可知,汽车是8:20到站,火车是8:25到站,用火车到站时刻减去汽车到站时刻,即可求出汽车比火车早到多少分钟。
(2)从图中可知,汽车是7:55出发,8:20到站,共行驶15千米;先用到站时刻减去出发时刻,求出汽车行驶的时间;再根据“速度=路程÷时间”,求出汽车的速度。
【详解】(1)看图填空:
①8时10分-8时=10(分钟)
10÷60=(小时)
火车中途停站时间是小时。
②8时25分-8时20分=5(分钟)
汽车比火车早到5分钟。
(2)8时20分-7时55分=25(分钟)
15÷25=0.6(千米)
答:汽车的速度是每分钟0.6千米。
5.图见详解
(1)0~1岁;26厘米
(2)图见详解;发现:我在0~1岁这一年长得最快
【分析】根据统计表中的数据,先描点,再连线,画出相应的折线统计图。
(1)根据折线统计图可知,小东0~1岁这一年长得最快,用1岁的身高减去0岁的,求出长高了多少厘米;
(2)根据自己的身高数据,先整理出自己0~10岁的身高情况,然后画出折线统计图,并从中获得信息,分析解答即可。
【详解】
(1)76-50=26(厘米)
答:小东0~1岁这一年长得最快,这一年长高了26厘米。
(2)我的0~10岁身高情况统计表:
年龄 0 1 2 3 4 5 6 7 8 9 10
身高/厘米 50 75 85 98 110 117 125 132 142 148 150
答:我发现我在0~1岁这一年长得最快。
(答案不唯一)
6.(1)B;5
(2)20;15;
(3)B;B无人机的飞行时间更长、从整体看,B无人机飞得更高
(4)8
【分析】(1)观察复试折线统计图,横轴表示飞行时间,纵轴表示飞行高度。观察A、B两架无人机飞行时间分别是35秒和40秒,求出两者之差即可。
(2)观察A的折线统计图第10秒在20米的高度,两条折线相交的点在纵轴的位置就是同一高度。分别找到A在25秒是高度20米,B在25秒时高度是25米,用20÷25即可。
(3)观察飞行时间和飞行高度,飞行时间越长,高度越高的飞行情况就好些,据此解答。
(4)老师首先用1分钟通知第一个学生;1+1=2,第二分钟由老师和1个学生两人分别通知1个学生,现在通知的一共2+2-1=3个学生;第三分钟可以推出通知的一共4+4-1=7个学生;还有1名同学,第四分钟通知,由此问题解决。
【详解】(1)A无人机飞行时间是35秒,B无人机飞行时间是40秒。
35<40,40-35=5(秒)
即,观察上图,我发现B无人机飞行的时间更长一些,两架无人机的飞行时间相差5秒。
(2)A无人机第10秒在20米的高度,起飞后第15秒两架无人机在同一高度。
20÷25==
即,起飞后第10秒时,A无人机的飞行高度是20米,起飞后第15秒时,两架无人机处于同一高度,第25秒时,A无人机飞行高度是B无人机飞行高度的。
(3)我认为B无人机的飞行情况更好些,理由是;B无人机的飞行时间更长、从整体看,B无人机飞得更高。
(4)第一分钟通知到1名同学;
第二分钟最多可通知到3名同学;
第三分钟最多可通知到7名同学;
第四分钟时可以通知到第8名同学。即,最少需要4分钟。
7.(1)0.9;
(2)45;
(3)20千米
【分析】(1)由折线统计图可知:甲、乙两名大学生骑电动车20分钟走了18千米,根据路程÷时间=速度,用18÷20可求出电动车的速度是0.9千米/分。
(2)由题意可知:甲步行所用的时间等于乙骑电动车行驶(36-13.5+18)千米的时间。根据路程÷速度=时间,用(36-13.5+18)÷0.9可求出甲步行所用的时间是45分钟。
(3)由题意可知:甲步行45分钟所走的路程是36-13.5-18=4.5(千米),根据路程÷时间=速度,用4.5÷45可求出甲步行的速度是0.1千米/分;乙返回到学校用了20分钟,根据速度×时间=路程,用0.1×20可求出甲20分钟所走的路程是2千米;最后用2千米加上甲、乙骑电动车所走的18千米可求出甲与学校相距的千米数。
【详解】(1)18÷20=0.9(千米/分)
所以,电动车的速度为0.9千米/分。
(2)(36-13.5+18)÷0.9
=(22.5+18)÷0.9
=40.5÷0.9
=45(分)
所以,甲步行所用的时间为45分。
(3)(36-13.5-18)÷45
=4.5÷45
=0.1(千米/分)
0.1×20+18
=2+18
=20(千米)
答:甲与学校相距20千米远。
8.(1)35
(2)20;10
(3)1;0.5
(4)17.5千米/时
【分析】(1)观察图象可知,小明骑自行车离家最远的距离对应的是最上面的一段,即在12时~13时,距离为35千米。
(2)观察图象可知,小明骑自行车行驶过程中,行驶最快时对应的线段最陡,行驶最慢时对应的线段最平缓;
即小明在10时~10.5时对应的速度最快,在11时~12时的速度最慢;根据“速度=路程÷时间”,分别求出最快的车速度和最慢的车速。
(3)在10.5时~11时,线段水平,表示这段时间的路程不变,此时小明在休息,据此解答。
(4)小明离家最远的地方是35千米,返回家一共用时(15-13)时,根据“速度=路程÷时间”,即可求出返回家时的平均速度。
【详解】(1)小明骑自行车离家最远的距离是35千米。
(2)小明在10时~10.5时骑车速度最快:
(25-15)÷(10.5-10)
=10÷0.5
=20(千米/时)
在11时~12时骑车速度最慢:
(35-25)÷(12-11)
=10÷1
=10(千米/时)
小明骑自行车行驶过程中,最快的车速是20千米/时,最慢的车速是10千米/时。
(3)11-10.5=0.5(小时)
去的途中小明休息了1次,共休息了0.5小时。
(4)35÷(15-13)
=35÷2
=17.5(千米/时)
答:小明由离家最远的地方返回家时的平均速度是17.5千米/时。
【点睛】结合距离和时间的关系图象,考查对不同时间段运动状态的分析,并根据速度、时间、路程之间的关系解答。
9.(1)小红;见详解
(2)见详解
【分析】(1)观察复式折线统计图中两条折线的变化趋势,得出小红的跳绳成绩更好、更稳定。
(2)从统计图中获取信息,写出两条有关的信息,合理即可。
【详解】(1)我认为派小红去比较合适。
因为从统计图中可以看出,第5次~第10次小红跳绳个数基本呈递增趋势,而小亮跳绳个数时增时减,所以应该派小红参加比赛。(原因不唯一)
(2)从图中还能得到以下信息:
①小红一分钟跳绳成绩最好是167下,小亮一分钟跳绳成绩最好是165下。
②小红和小亮第6次的跳绳成绩相差5下。
(答案不唯一)
【点睛】理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
10.(1)二;四;(2)上升;157;(3)96;(4)本月第一周电视销售量比空调销售量多多少台?36台
【分析】(1)实线表示电视销售量,虚线表示空调销售量,观察实线的最低点在哪一周,则对应的一周电视销售量最少;观察虚线的最高点在哪一周,则对应的一周空调销售量最多;
(2)观察虚线的走向,发现本月空调销售量呈上升趋势,根据加法的意义,用22+35+44+56即可求出这个月的空调总销售量;
(3)根据加法的意义,用58+53+64+78即可求出这个月电视的总销售量;然后用这个月电视的总销售量减去空调的总销售量,即可求出这个月电视的总销售量比空调的总销售量多多少台;
(4)提出的问题合理即可,例如:本月第一周电视销售量比空调销售量多多少台。
【详解】(1)观察统计图可知,红旗商场第二周电视销售量最少,第四周空调销售量最多。
(2)22+35+44+56=157(台)
根据分析可知,本月空调销售量呈上升趋势,共销售空调157台。
(3)58+53+64+78=253(台)
253-157=96(台)
这个月电视的总销售量比空调的总销售量多96台。
(4)问题:本月第一周电视销售量比空调销售量多多少台?
58-22=36(台)
答:本月第一周电视销售量比空调销售量多36台。(答案不唯一)
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)复式折线
(2)十一;七
(3)下半年毛衣销售量呈上升趋势,下半年衬衫销售量呈下降趋势。
【分析】(1)根据统计图的特点可知,这个图是复式折线统计图;
(2)代表毛衣和衬衫的折线上的最高点表示销售量最大;
(3) 折线向上表示呈上升趋势,折线向下表示呈下降趋势。(答案不唯一)
【详解】(1)上图为复式折线统计图。
(2)毛衣的销售量在十一月最大,衬衫的销售量在七月最大。
(3)下半年毛衣销售量呈上升趋势,下半年衬衫销售量呈下降趋势。
【点睛】本题考查复式折线统计图,通过统计图分析出相应的数据是解题的关键。
12.(1)见详解;
(2)随着年级的升高,男、女生近视的人数逐渐增多;(答案不唯一)
(3);
(4)见详解
【分析】(1)统计图中横轴表示年级,纵轴表示人数,单位长度表示2人,根据表格中的数据描出表示女生近视人数的各点,再用实线依次连接各点,最后在各点处标出对应的数据;
(2)如果折线统计图中的折线呈上升趋势,那么近视人数增多;如果折线统计图中的折线呈下降趋势,那么近视人数减少;
(3)五年级男生近视人数有18人,女生近视人数有22人,A是B的几分之几的计算方法:A÷B=,结果化为最简分数;
(4)一至六年级男、女生近视的人数越来越多,同学们应多做眼保健操、注意用眼卫生、保护视力,言之有理即可。
【详解】(1)分析可知:
(2)观察复式折线统计图可知,随着年级的升高,男、女生近视的人数逐渐增多。(答案不唯一)
(3)18÷22=
所以,五年级男生近视人数是女生近视人数的。
(4)同学们平时应注意用眼卫生,多做眼保健操,减少看电子产品的时间,保护视力。(答案不唯一)
【点睛】掌握折线统计图的特点及作用和一个数占另一个数几分之几的计算方法是解答题目的关键。
13.(1)6;10;9;(2)见详解;(答案不唯一)
【分析】(1)利用减法分别计算6-11岁之间测量硕硕的体重与同龄男孩标准体重之间的差值,比较6-11岁之间差值的大小,即可求出硕硕的体重在几岁时最接近标准体重以及在几岁时与标准体重相差最大。依次用硕硕7岁时体重减去6岁时的体重,8岁时体重减去7岁时的体重,9岁时体重减去8岁时的体重,10岁时体重减去9岁时的体重,11岁时体重减去10岁时的体重,求出当前岁数比上一年增长的体重,比较每一年增长体重的大小,即可求出在几岁时比上一年增长的幅度最大。
(2)观察统计图,实线数据整体高于虚线数据,表示硕硕的体重高于标准体重,建议合理即可。
【详解】(1)24-21=3(千克)
28-22=6(千克)
31-23=8(千克)
36-26=10(千克)
40-28=12(千克)
42-31=11(千克)
3<6<8<10<11<12
即硕硕的体重在6岁时最接近标准体重;在10岁时与标准体重相差最大。
28-24=4(千克)
31-28=3(千克)
36-31=5(千克)
40-36=4(千克)
42-40=2(千克)
2<3<4<5
即在9岁时比上一年增长的幅度最大。
(2)答:我给硕硕的建议是少吃高脂肪含量的食品,多多运动。(答案不唯一,合理即可)
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)4;43;
(2)3月份甲种饮料的销量占乙种饮料销量的几分之几?;(答案不唯一)
(3)见详解
【分析】(1)复式折线统计图中,横轴表示月份,纵轴表示销量,单位长度表示25件,两条折线之间的距离越大,两种饮料销量相差越大,两条折线之间的距离越小,两种饮料销量相差越小;
(2)3月份甲种饮料的销量占乙种饮料销量的几分之几?A是B的几分之几的计算方法:A÷B=,结果化为最简分数;
(3)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,根据两种饮料销量的变化趋势分析问题,据此解答。
【详解】(1)4月份两点的距离最大。
96-53=43(件)
由复式折线统计图可知,4月份两种饮料销量相差最大,相差43件。
(2)数学问题:3月份甲种饮料的销量占乙种饮料销量的几分之几?
56÷70=
答:3月份甲种饮料的销量占乙种饮料销量的。(答案不唯一)
(3)观察复式折线统计图可知,甲种饮料的销量呈逐渐上升的趋势,乙种饮料的销量1月-2月,3月-4月呈下降趋势,2月-3月呈上升趋势,甲种饮料越来越畅销,建议超市经理进货时多进甲种饮料,少进乙种饮料。(答案不唯一)
【点睛】掌握折线统计图的特点及作用和一个数占另一个数几分之几的计算方法是解答题目的关键。
15.(1)见详解;(2)王芳;王芳的成绩比较好
【分析】(1)根据表格的数据在统计图上描出各点,再依次连接即可,实线表示王芳的数据,虚线表示李红的数据;
(2)观察统计图可知,王芳的成绩稳步上升,李红的成绩不稳定,所以派王芳去参加比赛比较合适。
【详解】(1)如图:
(2)派王芳去参加比赛比较合适,因为王芳的成绩比较好。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
16.(1)见详解;(2)A品牌;(3)见详解
【分析】(1)折线统计图的绘制方法是:先整理数据;利用纵轴和横轴上的长度单位所表示的数量,根据数量的多少描出各点,再把各点用线段顺次连接起来。
(2)观察折线统计图,实线代表A手机的销售情况,虚线代表B手机的销售情况,从两条折线的总体情况来看,在这6个月中A手机比B手机的总体情况要好一些。
(3)在1-2月A品牌的手机销量是往上增长,从2月开始,呈下降的趋势;B品牌的手机销量在前3个月起起伏伏,从3月开始,呈上升的趋势。
【详解】(1)如图:
(2)答:A品牌手机在这6个月中总销售量较好。
(3)答:从销售情况来看,A品牌手机的销售情况呈下降的趋势,B品牌手机的销售情况呈上升的趋势。
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)2800
(2)见详解
(3)
【分析】(1)根据:平均数=总数÷份数,求出B品牌四个季度的平均销售数量,再加上50台即可计算出A品牌电视机在第二季度销售台数;
(2)A品牌电视机第四季度的销售数量与第三季度的销售数量持平,第三季度是3000台,那么第四季度也是3000台,再根据(1)中A品牌电视机在第二季度的销售数量,补充折线即可;
(3)求第三季度中,B品牌电视机的销售数量相当于A品牌的几分之几,用B品牌电视机第三季度的销售数量除以A品牌第三季度的销售数量,结果用分数表示即可。
【详解】(1)(2400+2700+2800+3100)÷4
=(5100+2800+3100)÷4
=11000÷4
=2750(台)
2750+50=2800(台)
所以,A品牌电视机在第二季度销售了(2800)台。
(2)作图如下:
(3)2800÷3000=
所以,在第三季度中,B品牌电视机的销售数量相当于A品牌的。
【点睛】此题考查了折线统计图、平均数以及分数与除法的关系,关键能够从统计图获取正确信息再解答。
18.(1)见详解;
(2)15;6
(3)数学成绩不稳定波动较大,需要多加练习(答案不唯一)
【分析】(1)统计图中横轴表示次数,纵轴表示成绩,单位长度表示2分,根据表格中的数据画出表示语文和数学每次的分数,再用实线依次连接表示语文分数的各点,用虚线依次连接表示数学分数的各点,最后标出对应的数据;
(2)折线统计图中折点越高对应的分数越高,折点越低对应的分数越低,分别找出数学和语文的最高分和最低分,再求出它们的差;
(3)复式折线统计图中表示数学成绩的折线波动较大,成绩不稳定,表示语文成绩的折线波动较小,成绩稳定,应多做习题巩固知识,数学成绩稳步提升,据此解答。
【详解】(1)分析可知:
(2)由复式折线统计图可知,数学最高分为95分,最低分为80分,语文最高分为89分,最低分为83分。
95-80=15(分)
89-83=6(分)
所以,数学最高分比最低分高15分,语文最高分比最低分高6分。
(3)观察复式折线统计图可知,洋洋的数学成绩不稳定波动较大,需要多加练习。(答案不唯一)
【点睛】本题主要考查统计图表的综合应用,掌握折线统计图的特点及作用是解答题目的关键。
19.(1)见详解;(2)踢足球;6;(3)五年级喜欢打篮球和踢足球的人数一共有多少人?;168人
【分析】(1)根据表格数据绘制折现统计图即可;(2)分别计算出五年级喜欢打篮球和喜欢踢足球的总人数,再进行比较即可得出结论;(3)根据表格数据可计算出五年级喜欢打篮球和踢足球的总人数,本小题的答案并不唯一,符合题意即可。
【详解】(1)折线统计图如下:
(2)喜欢打篮球:13+16+8+17+12+15=81(人)
喜欢踢足球:18+11+14+16+9+19=87(人)
87-81=6(人)
因此希望小学五年级学生喜欢踢足球的人数多,比喜欢打篮球的多6人。
(3)可提的数学问题:五年级喜欢打篮球和踢足球的人数一共有多少人?
13+16+8+17+12+15+18+11+14+16+9+19=168(人)
答:五年级喜欢打篮球和踢足球的人数一共有168人。
【点睛】解答本题的关键是抓住图表信息,结合问题进行分析即可完成解答。
20.(1)见详解。
(2)13:00;16
(3)上升
【分析】(1)横轴表示时刻,纵轴表示气温,一个单位长度表示2℃。先根据统计表中的数据,在横上找到相应时刻的点,在纵轴上找到该时刻所对应的气温的点,过两点分别过横轴、纵轴的垂线,两条垂线的交点就是所要描的点,在交点处点上实心点;将所有的实心点用线段顺次连接起来,并在所描点的上方或下方标上数据。
(2)先找到折线统计图上的最高点,再过最高点作横轴的垂线,垂足处的时刻即是气温最高时的时刻;用折线统计图上最高点对应的气温减去最低点对应的气温,即可求出最高与最低气温的温差。
(3)观察折线统计图发现:表示该日7:00至13:00的折线呈上升趋势,即该日7:00至13:00的气温变化趋势是上升趋势。
【详解】(1)如下图:
(2)折线上最高点所对应的时刻是13:00,最高点所对应的气温是24℃,最低点所对应的气温是8℃,24-8=16(℃),所以13:00的气温最高,最高与最低气温相差了16℃。
(3)通过观察折线统计图可知,该日7:00至13:00的气温变化趋势是上升。
【点睛】运用横向、纵向、综合、对比等不同的观察方法,可以读懂折线统计图,从中获取更多的信息,并能根据信息回答或提出相应的问题,同时进行简单的分析和合理的预测。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
