广东省深圳实验学校(中学部)2023-2024学年第二学期七年级数学期中阶段检测(含答案)
文档属性
| 名称 | 广东省深圳实验学校(中学部)2023-2024学年第二学期七年级数学期中阶段检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 445.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 09:47:59 | ||
图片预览




文档简介
实验学校(中学部)2023-2024学年度第二学期阶段检测
七年级 数学试卷
考试时间:90分钟 试卷满分:100分
说明:请考生在答题卷指定区域按要求规范作答,考试结束上交答题卷
一 .选择题(共10小题)
1. 下列计算正确的是( )
A.3a+2a=5a B.-(a-2)=-a-2 C.a ·a =a D.(a-1) =a -1
2. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物, 世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39 的原生动物,它的最长直径
也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10- B.3×10- C.3×10- D.3×10
3. 如图,要把河中的水引到村庄A, 小凡先作AB⊥CD, 垂足为点B, 然后沿AB 开挖水
渠,就能使所开挖的水渠最短,其依据是( )
A. 两点确定一条直线
B. 两点之间线段最短
C. 直线外一点与直线上各点连接的所有线段中,垂线段最短
D. 三角形两边之和大于第三边
4. 如图,点E 在 AD 延长线上,下列条件中不能判定BC/IAD 的是( )
A.∠1=∠2 B.∠C=∠CDE C. ∠3=∠4 D.∠C+∠ADC=180°
第1页(共22页)
5. 下 列 说 法 正 确 的 是 ( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
6. 下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( )
A.4cm B.6cm C.8cm D.10cm
7. 如图,在AABC中 ,BD是AABC的中线, BE 是AABD的中线,若AE=3, 则AC的长
度为( )
A.3 B.6 C.9 D.12
8. 一 副直角三角板按如图所示的方式放置,点E 在 边BC 的延长线上, BE/IDF,
∠B=∠DEF=90°, 则 ∠CDE 的度数为( )
A.30° B.25° C.20° D.15°
第2页(共22页)
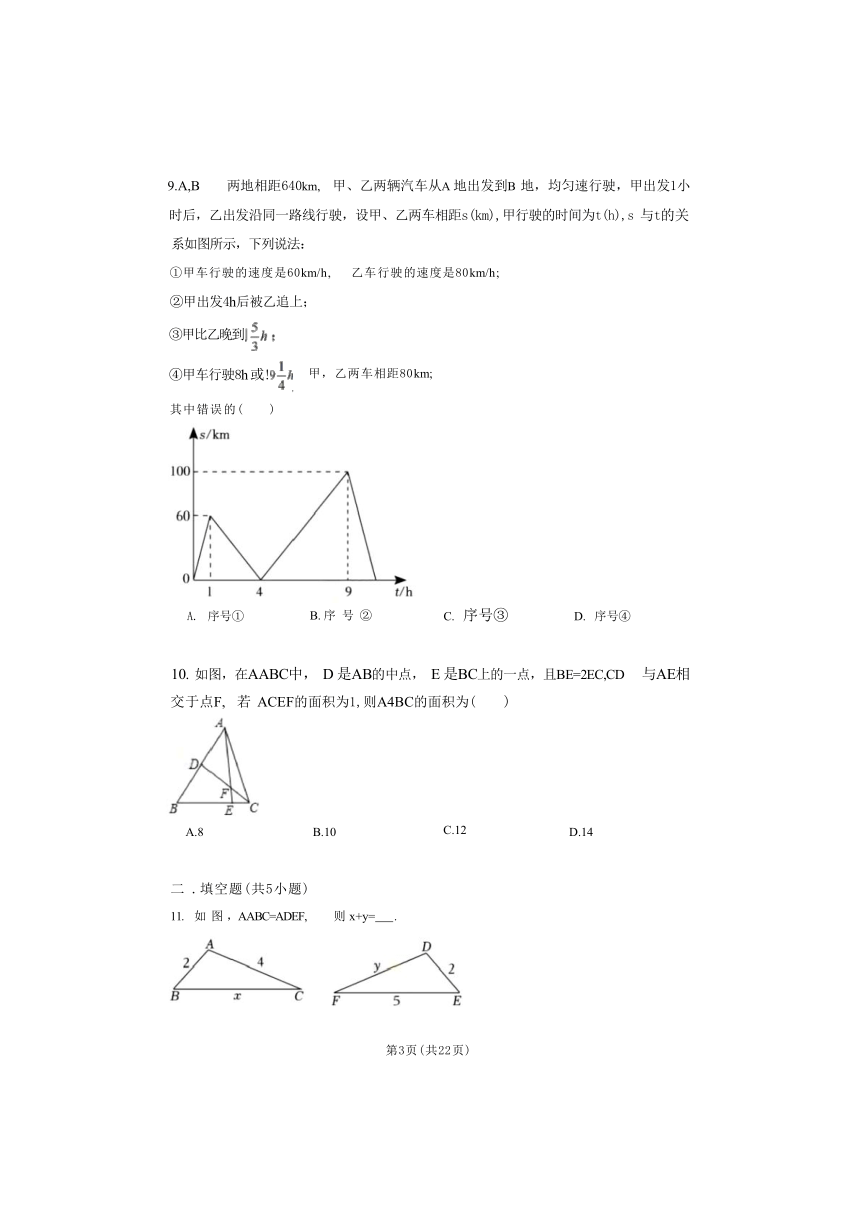
9.A,B 两地相距640km, 甲、乙两辆汽车从A 地出发到B 地,均匀速行驶,甲出发1小 时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s 与t的关
系如图所示,下列说法:
①甲车行驶的速度是60km/h, 乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到
④甲车行驶8h 或!
,
甲,乙两车相距80km;
其中错误的( )
A. 序号① B. 序 号 ② C. 序号③ D. 序号④
10. 如图,在AABC中, D 是AB的中点, E 是BC上的一点,且BE=2EC,CD 与AE相
交于点F, 若 ACEF的面积为1,则A4BC的面积为( )
A.8
B.10
C.12
D.14
二 .填空题(共5小题)
11. 如 图 ,AABC=ADEF,
则 x+y= .
第3页(共22页)
12. 一个等腰三角形的两边长分别是3cm 和7cm, 则它的周长是 cm.
13. 已知2x+y-3=0, 则2”·4 的值是
14.如图,已知∠MAN=55°, 点B 为AN上一点.用尺规按如下过程作图:以点A 为圆心, 以任意长为半径画弧,交AN于点D, 交AM于点E; 以点B为圆心,以AD长为半径作弧,
交AB于点F; 以点F 为圆心,以DE 长为半径作弧,交前面的弧于点G, 连接BG 并延长
交AM 于点C, 则∠BCM=
15. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB/IDE,
∠D=70°, 则∠ACD=
三 .解答题(共7小题)
16. 计算:
(2)2023 -2024×2022;
(3)(2x y) ·(-2y)+(-2x'y)+(2x):
(4)(x+4) -(x+2)(x-5).
17.先化简,再求值:[(x+y)(x-y)-(x-2yy -3y ]÷4y, 其中x=2024,y=-1.
第4页(共22页)
18. 看图填空:已知如图,AD⊥BC 于D,EG⊥BC 于G,∠E=∠1,
求证:AD 平分∠BAC.
证明:∵AD⊥BC于 D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90( ).
∴∠ADC=∠EGC (等量代换).
∴AD//EG( ).
∴∠1=∠2( ),
∠E=∠3( ).
又∵∠E=∠1 (已知),
∴∠2=∠3(__).
∴AD 平分∠BAC(__).
19. 如图,在AABC中,∠ABC=82°,∠C=58°,BD⊥AC 于D,AE 平分∠CAB,BD 与
AE交于点F, 求∠AFB.
第5页(共22页)
20. 已知AABC的三边长为a,b,c, 且a,b,c 都是整数.
(1)若a=2,b=5, 且c 为偶数.求AABC 的周长.
( 2 ) 化 简 : |a-b+c|-|b-c-a|+|a+b+c|;
21.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到
(a+b) =a +2ab+b , 基于此,请解答下列问题:
(1)①若xy=8,x+y=6, 则x +y 的值为
②若x(5-x)=6, 则x +(5-x) =
(2)两块完全相同的特制直角三角板(∠AOB=∠COD=90) 如图2所示放置,其中A,O,
D 在一直线上,连接AC,BD, 若AD=14,So+Sxmop=54, 求一块三角板的面积.
图 1
图 2
第6页(共22页)
22.【基础探究】
(1)如图1,AB//CD, 点E 是CD 上的点,点P 是AB 和CD 之间的一点,连接PB、PE. 若
∠B=25°,∠PEC=32°, 请你求出∠P 的度数;
(2)如图2,BEIIDF,∠DBE 的平分线与∠CDF的平分线交于点G, 当∠BGD=65°时,
则∠BDC的度数为
(3)如图3,DHIIEG, 点A、点 C 分别是DH 、EG 上的点,点B 和点F 是DH 和EG
之间的点,连接AB 、AF 、CB 、CF. 若∠B=94°,∠F=92°,AF 、CB 分别平分∠HAB、
∠GCE, 则∠BAH 的度数为
【问题迁移】
(4)如图4,在AABC 中,∠A=60°,BO 、CO 分别平分∠ABC、∠ACB. 则∠BOC=
【拓展深化】
如图,在AABC 中 ,D 、E 是 AB 、AC 上的点,设∠AED=m°,∠C=n(m(5)如图5, BO、DO 分别平分∠ABC、∠BDE. 用含m 、n 的式子表示∠BOD的度数
为
图 1
图 4
图 2
图 5
图 3
第7页(共22页)
2023-2024学年实验学校(中学部)七下期中数学试卷
参考答案与试题解析
一 .选择题(共10小题)
1. 下列计算正确的是( )
A.3a+2g=5g B.-(a-2)=-a-2 C.a ·a =a D.(a-1) =a -1
【解答】解:3a+2a=5a, 则A不符合题意;
-(a-2)=-a+2, 则B 不符合题意;
a ·a =a ,则C 符合题意;
(a-1) =a -2a+1, 则 D 不符合题意;
故选:C.
2. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物, 世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39 的原生动物,它的最长直径
也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10- B.3×10 C.3×10-7 D.3×10
【解答】解:0.0000003=3×10- .
故选: C.
3. 如图,要把河中的水引到村庄A, 小凡先作AB⊥CD, 垂足为点B, 然后沿AB开挖水
渠,就能使所开挖的水渠最短,其依据是()
D
A. 两点确定一条直线
B. 两点之间线段最短
C. 直线外一点与直线上各点连接的所有线段中,垂线段最短
D. 三角形两边之和大于第三边
【解答】解:先过点A 作AB⊥CD, 垂足为点B, 然后沿AB 开渠,能使所开的渠道最短,
这样设计的依据是垂线段最短;
故选: C.
第8页(共22页)
4. 如图,点E 在AD延长线上,下列条件中不能判定BC//AD 的是( )
A.Z1=∠2 B. ∠C=∠CDE C. ∠3=∠4
D. ∠C+∠ADC=180°
【解答】解: A、∵∠1=∠2,
∴AB/ICD, 本选项符合题意;
B、∵∠C=∠CDE,
∴BC/IAD, 本选项不合题意;
C、∵∠3=∠4,
∴BC/IAD, 本选项不合题意;
D、∵∠C+∠ADC=180°,
∴AD//BC, 本选项不符合题意.
故选: A.
5. 下列说法正确的是( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
【解答】解: A. 不相交的两条直线互相平行,错误,应为:同一平面内:不相交的两条
直线互相平行.
B. 垂直于同一条直线的两条直线互相平行,错误.应为:同一平面内:垂直于同一条直
线的两条直线互相平行.
C. 经过直线外一点有且只有一条直线与这条直线平行,正确.
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交,错误,应为:同一平
第9页(共22页)
面内,两条直线的位置关系有两种:平行、相交.
故选: C.
6. 下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( )
A.4cm B.6cm C.8cm D.10cm
【解答】解:因为弹簧伸长的长度与所挂的物体的重量成正比,设y=kx+b,
由表格得:
解得:
∴y=2x+8,
当x=0 时, y=8,
故选: C.
7. 如图,在AABC 中, BD是AABC的中线, BE是AABD的中线,若AE=3, 则AC的
长度为( )
A.3 B.6 C.9 D.12
【解答】解:∵BE 是AABD的中线,
∴AD=2AE=6,
∵BD 是AABC 的中线,
∴AC=2AD=12,
故选: D.
8. 一副直角三角板按如图所示的方式放置,点E 在 边BC 的延长线上, BE/IDF,
∠B=∠DEF=90°, 则∠CDE 的度数为( )
第10页(共22页)
A.30° B.25° C.20° D.15°
【解答】解:∵A4BC,AEFD 为直角三角板,
∴∠ACB=60°,∠EDF=45°
∵BEIIDF,
∴∠FDC=∠ACB=60°,
∴∠CDE=∠FDC-∠EDF=60°-45°=15°,
故选: D.
9.A,B 两地相距640km, 甲、乙两辆汽车从A地出发到B 地,均匀速行驶,甲出发1小 时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km), 甲行驶的时间为r(h),s 与t 的关
系如图所示,下列说法:
①甲车行驶的速度是60km/h, 乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到
①甲车行坡3动或5.甲,乙两车相距8t
其中错误的( )
A. 序号① B. 序号② C. 序号③ D. 序号④
【解答】解:①由图可得,甲车行驶的速度是60÷1=60(km/h),
∵甲先出发1h, 乙出发3h 后追上甲,
第11页(共22页)
∴3(v-60)=60,
∴Vz=80(km/h),
即乙车行驶的速度是80km/h, 故①正确;
②∵当t=1 时,乙出发,当t=4 时,乙追上甲,
:甲出发4h 后被乙追上,故②正确;
③由图可得,当乙到达B 地时,甲乙相距100km,
:.甲比乙晚到 ,故③正确;
④应该分两种情况讨论:i 乙车行驶过程中超前甲车80km,ii 乙车到达B 地,而甲车离B 地还有80km、当乙车尚在行驶中,且超前甲车80km时由图可得当60r+80=80(t-1) 时,解
得t=8;ii、 当乙车到达B 地,而甲车离B 地还有80km 时,
∵A地和B 地之间的距离是640km, 且甲车出发1小时后乙车才出发,
∴80(t-I)=640, 解得t=9, 即乙车在t=9 时到达B 地由图可得,60t+80=640 时,甲车
离B 地80km, 解得
3.甲车有数成:.甲,乙所年相an, 数3措
故选:D.
10. 如图,在AABC中 ,D 是AB的中点, E 是BC上的一点,且BE=2EC,CD 与AE相
交于点F, 若 ACEF的面积为1,则AABC的面积为( )
A.24 B.25 C.30 D.32
【解答】解:连接BF,
∵BE=2EC,
∴S mE=2Src=2,
设SpF=X
∵AD=BD
∴S DF=SABDF=X,SADC =SAaDC
第12页(共22页)
∴SDc-SAADF=SABDC-SABDF=3
∵BE =2EC
∴SE=2S
∴2x+2=2x4
∴x=3
∴Sac =SuDp+SAaDp+SAaFE+SAAE=12
故选: C,
二 .填空题(共5小题)
11. 如图,△ABC=ADEF, 则 x+y=_9
【解答】解:∵△ABC=ADEF,
∴BC=FE=5,DF=AC=4,
∴x=5,y=4,
∴x+y
=5+4
=9.
故答案为:9.
12. 一个等腰三角形的两边长分别是3cm和7cm, 则它的周长是 cm.
【解答】解:①当腰是3cm, 底边是7cm时:不满足三角形的三边关系,因此舍去.
②当底边是3cm, 腰长是7cm 时,能构成三角形,则其周长=3+7+7=17(cm).
故答案为:17.
13.已 知 2x+y-3=0, 则2° ·4*的值是8
【解答】解:由题意,得
2x+y=3.
第13页(共22页)
2'·4 =2 -2 =2 +=2 =8,
故答案为:8.
14. 如图,已知∠MAN=55°, 点B为AN上一点.用尺规按如下过程作图:以点A为圆心, 以任意长为半径画弧,交AN于点D, 交AM于点E; 以点B为圆心,以AD长为半径作弧, 交AB于点F; 以点F 为圆心,以DE长为半径作弧,交前面的弧于点G, 连接BG并延长
交AM于点C, 则∠BCM=__ 110°_.
【解答】解:由作法得∠ABC=∠A=55°,
所以∠BCM=∠A+∠ABC=55°+55°=110°,
故答案为:110°
15. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB/IDE,
∠D=70°, 则∠ACD=_20°_.
【解答】解:过点C 作CF//AB,
∵ABIIDE,
∴CF//DE,
∴∠ACF=∠BAC,∠D+∠DCF=180°,
又∠BAC=130°,∠D=70°,
∴∠ACF=130°,∠DCF=110°,
∴∠ACD=∠ACF-∠DCF=20°.
故答案为:20°.
第14页(共22页)
三 .解答题(共7小题)
16. 计算:
(2)2023 -2024×2022;
(3)(2x y) ·(-2xy)+(-2x y)÷(2x );
(4)(x+4) -(x+2)(x-5) ·
【解答】解:(1)原式=-17
(2)原式=1
(3)原式=12x y
(4)原式=11x+26
17. 先化简,再求值:[(x+y)(x-y)-(x-2y) -3y ]÷4y, 其中x=2024,y=-1.
【解答】解:原式=[x -y -(x -4xy+4y )-3y ]÷4y
=(x -y -x +4xy-4y -3y )÷4y
=(-8y +4xy)÷4y
=-2y+x,
当x=2024,y=-1 时,
原式=-2×(-1)+2024
=2+2024
=2026.
18. 看图填空:已知如图, AD⊥BC于D,EG⊥BC 于G,∠E=∠1,
求证: AD平分∠BAC.
证明:∵AD⊥BC 于D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90( 垂直的定义 ).
∴∠ADC=∠EGC (等量代换).
∴AD//EG( ).
∴∠1=∠2( ),
第15页(共22页)
∠E=∠3( ).
又∵∠E=∠1 (已知),
∴∠2=∠3(__).
∴AD平分∠BAC(_).
【解答】证明:
∵AD⊥BC于D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90° (垂直的定义),
∴∠ADC=∠EGC (等量代换),
∴AD/IEG (同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3 (两直线平行,同位角相等),
又∵∠E=∠1 (已知),
∴∠2=∠3(等量代换),
∴AD平分∠BAC (角平分线的定义).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,
同位角相等;等量代换;角平分线的定义.
19. 如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC 于D,AE 平分∠CAB,BD 与
AE交于点F, 求∠AFB.
【解答】解:∵∠CAB=180°-∠ABC-∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
第16页(共22页)
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
20. 已知△ABC的三边长为a,b,c, 且a,b,c 都是整数.
(1)若a=2,b=5. 且c 为偶数.求AABC的周长.
(2)化简: |a-b+c|-|b-c-a|+|a+b+c|;
【解答】解:
(1)∵a=2,b=5,
∴5-2即 3∵c是偶数,则c=4 或6,
当c=4 时, AABC的周长为a+b+c=2+5+4=11,
当c=6 时, AABC 的周长为a+b+c=2+5+6=13,
综上所述, AABC的周长为11或13.
(2)∵AABC 的三边长为a,b,c,
∴a+c>b,
:|a-b+c|-|b-c-a|+|a+b+cl
=a+c-b-(a+c-b)+a+b+c
=a+b+c;
21.【阅读理解】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如
图1可以得到(a+b) =a +2ab+b , 基于此,请解答下列问题:
【类比应用】
(1)①若xy=8,x+y=6, 则x +y 的值为
②若x(5-x)=6, 则x +(5-x) =
【迁移应用】
第17页(共22页)
(2)两块完全相同的特制直角三角板(∠AOB=∠COD=90°) 如图2所示放置,其中A,O,
D在一直线上,连接AC,BD, 若AD=14,Soc+Smop=54, 求一块三角板的面积.
图 1 图 2
【解答】解:(1)①由题意可知, x +y =(x+y) -2xy,
∵xy=8,x+y=6,
∴x +y =6 -2×8=20,
故答案为:20.
②令a=x,b=5-x,
∴a+b=5,ab=6,
∴x +(5-x) =a +b =(a+b} -2ab=5 -2×6=13,
故答案为:13.
(2)设三角板的两条直角边AO=m,BO=n, 则一块三角板的面积为 ∴m+n=14, · ,即m +n =108,
∵2mn=(m+m) -(m +n )=14 -108=88,
∴mn=44,
:一块三角板的面积是22.
22.【基础探究】
(1)如图1,AB//CD, 点E 是CD 上的点,点P 是AB 和CD 之间的一点,连接PB、PE. 若
∠B=25°,∠PEC=32°, 则∠P 的度数为_57°_ ;
(2)如图2, BE//DF,∠DBE 的平分线与∠CDF的平分线交于点G, 当∠BGD=65°时,
则∠BDC 的度数为 ;
第18页(共22页)
(3)如图3, DHIIEG, 点A 、点C 分别是DH 、EG 上的点,点B 和点F 是DH 和EG 之间的点,连接AB 、AF 、CB 、CF. 若∠B=94°,∠F=92°,AF 、CB 分别平分∠HAB、
∠GCE, 则∠BAH的度数为
【问题迁移】
(4)如图4,在△ABC中 ,BO 、CO分别平分∠ABC、∠ACB.则∠BOC与∠A的数量关
系为: ∠BOC=
【拓展深化】
如图,在AABC 中 ,D 、E 是 AB 、AC 上的点,设∠AED=m°,∠C=n°(m(5)如图5,BO、DO 分别平分∠ABC、∠BDE. 用含m 、n 的式子表示∠BOD的度数
为 ;
图 1
图 4
图 2
图 5
图 3
【解答】解:(1)过点P 作 PNHAB, 如图1所示:
∵AB ICD,
∴AB/IPN1ICD,
∴∠BPN=∠B,∠EPN=∠PEC,
∴∠BPN+∠EPN=∠B+∠PEC,
即∠BPE=∠B+∠PEC,
第19页(共22页)
∵∠B=25°,∠PEC=32°,
∴∠BPE=∠B+∠PEC=25°+32 =57°;
故答案为:57°
(2)设∠EBG=α,∠FDG=β, 如图2所示:
图2
∵∠DBE的平分线与∠CDF的平分线交于点G,
∴∠DBG=∠EBG=α,∠CDG=∠FDG=β,
∵BEIIDF,
由(1)可知:∠BGD=∠EBG+∠FDG=a+β,
∵∠BGD=65°,
∴a+β=65°,
∴∠DBG+∠CDG=a+β=65°,
由三角形的内角和定理得:
∠BGD+∠DGB+∠BDG=180°,
∴∠BGD+∠DGB+∠CDG+∠BDC=180°,
∴65°+65 +∠BDC=180°,
∴∠BDC=50°;
故答案为:50°.
(3)设∠HAF=α,∠GCB=β, 如图3所示:
图3
∵AF、CB 分别平分∠HAB、∠GCF,
∴∠BAF=∠HAF=a ∠BAH=2∠HAF=2a
∠GCF=2∠GCB=2β,
第20页(共22页)
∠GCF=∠GCB=β
∵DH IEG,
由(1)可知:∠B=∠HAB+∠GCB=2a+β,
∠F=∠HAF+∠GCF=α+2β,
∵∠B=94°,∠F=92°,
∴2a+β=94°,a+2β=92°,
解得:α=32°,β=30°
∴∠BAH=2a=64°,
故答案为:64°,
(4)如图1所示:
∵∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A,
∵BO 、CO分别平分∠ABC、∠ACB,
∴ ,
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC与∠A的数量关系是:
(5)延长 DE与BC的延长线交于点F, 如图5所示:
∵∠AED=m°,
∴∠FEC=∠AED=m°,
第21页(共22页)
∵∠ACB=∠FEC+∠F,∠ACB=n°(m∴∠F=∠ACB-∠FEC=n -m°,
∵BO、DO 分别平分∠ABC、∠BDE,
由(4)可知:
故答案为:
第22页(共22页)
七年级 数学试卷
考试时间:90分钟 试卷满分:100分
说明:请考生在答题卷指定区域按要求规范作答,考试结束上交答题卷
一 .选择题(共10小题)
1. 下列计算正确的是( )
A.3a+2a=5a B.-(a-2)=-a-2 C.a ·a =a D.(a-1) =a -1
2. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物, 世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39 的原生动物,它的最长直径
也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10- B.3×10- C.3×10- D.3×10
3. 如图,要把河中的水引到村庄A, 小凡先作AB⊥CD, 垂足为点B, 然后沿AB 开挖水
渠,就能使所开挖的水渠最短,其依据是( )
A. 两点确定一条直线
B. 两点之间线段最短
C. 直线外一点与直线上各点连接的所有线段中,垂线段最短
D. 三角形两边之和大于第三边
4. 如图,点E 在 AD 延长线上,下列条件中不能判定BC/IAD 的是( )
A.∠1=∠2 B.∠C=∠CDE C. ∠3=∠4 D.∠C+∠ADC=180°
第1页(共22页)
5. 下 列 说 法 正 确 的 是 ( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
6. 下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( )
A.4cm B.6cm C.8cm D.10cm
7. 如图,在AABC中 ,BD是AABC的中线, BE 是AABD的中线,若AE=3, 则AC的长
度为( )
A.3 B.6 C.9 D.12
8. 一 副直角三角板按如图所示的方式放置,点E 在 边BC 的延长线上, BE/IDF,
∠B=∠DEF=90°, 则 ∠CDE 的度数为( )
A.30° B.25° C.20° D.15°
第2页(共22页)
9.A,B 两地相距640km, 甲、乙两辆汽车从A 地出发到B 地,均匀速行驶,甲出发1小 时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s 与t的关
系如图所示,下列说法:
①甲车行驶的速度是60km/h, 乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到
④甲车行驶8h 或!
,
甲,乙两车相距80km;
其中错误的( )
A. 序号① B. 序 号 ② C. 序号③ D. 序号④
10. 如图,在AABC中, D 是AB的中点, E 是BC上的一点,且BE=2EC,CD 与AE相
交于点F, 若 ACEF的面积为1,则A4BC的面积为( )
A.8
B.10
C.12
D.14
二 .填空题(共5小题)
11. 如 图 ,AABC=ADEF,
则 x+y= .
第3页(共22页)
12. 一个等腰三角形的两边长分别是3cm 和7cm, 则它的周长是 cm.
13. 已知2x+y-3=0, 则2”·4 的值是
14.如图,已知∠MAN=55°, 点B 为AN上一点.用尺规按如下过程作图:以点A 为圆心, 以任意长为半径画弧,交AN于点D, 交AM于点E; 以点B为圆心,以AD长为半径作弧,
交AB于点F; 以点F 为圆心,以DE 长为半径作弧,交前面的弧于点G, 连接BG 并延长
交AM 于点C, 则∠BCM=
15. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB/IDE,
∠D=70°, 则∠ACD=
三 .解答题(共7小题)
16. 计算:
(2)2023 -2024×2022;
(3)(2x y) ·(-2y)+(-2x'y)+(2x):
(4)(x+4) -(x+2)(x-5).
17.先化简,再求值:[(x+y)(x-y)-(x-2yy -3y ]÷4y, 其中x=2024,y=-1.
第4页(共22页)
18. 看图填空:已知如图,AD⊥BC 于D,EG⊥BC 于G,∠E=∠1,
求证:AD 平分∠BAC.
证明:∵AD⊥BC于 D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90( ).
∴∠ADC=∠EGC (等量代换).
∴AD//EG( ).
∴∠1=∠2( ),
∠E=∠3( ).
又∵∠E=∠1 (已知),
∴∠2=∠3(__).
∴AD 平分∠BAC(__).
19. 如图,在AABC中,∠ABC=82°,∠C=58°,BD⊥AC 于D,AE 平分∠CAB,BD 与
AE交于点F, 求∠AFB.
第5页(共22页)
20. 已知AABC的三边长为a,b,c, 且a,b,c 都是整数.
(1)若a=2,b=5, 且c 为偶数.求AABC 的周长.
( 2 ) 化 简 : |a-b+c|-|b-c-a|+|a+b+c|;
21.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到
(a+b) =a +2ab+b , 基于此,请解答下列问题:
(1)①若xy=8,x+y=6, 则x +y 的值为
②若x(5-x)=6, 则x +(5-x) =
(2)两块完全相同的特制直角三角板(∠AOB=∠COD=90) 如图2所示放置,其中A,O,
D 在一直线上,连接AC,BD, 若AD=14,So+Sxmop=54, 求一块三角板的面积.
图 1
图 2
第6页(共22页)
22.【基础探究】
(1)如图1,AB//CD, 点E 是CD 上的点,点P 是AB 和CD 之间的一点,连接PB、PE. 若
∠B=25°,∠PEC=32°, 请你求出∠P 的度数;
(2)如图2,BEIIDF,∠DBE 的平分线与∠CDF的平分线交于点G, 当∠BGD=65°时,
则∠BDC的度数为
(3)如图3,DHIIEG, 点A、点 C 分别是DH 、EG 上的点,点B 和点F 是DH 和EG
之间的点,连接AB 、AF 、CB 、CF. 若∠B=94°,∠F=92°,AF 、CB 分别平分∠HAB、
∠GCE, 则∠BAH 的度数为
【问题迁移】
(4)如图4,在AABC 中,∠A=60°,BO 、CO 分别平分∠ABC、∠ACB. 则∠BOC=
【拓展深化】
如图,在AABC 中 ,D 、E 是 AB 、AC 上的点,设∠AED=m°,∠C=n(m
为
图 1
图 4
图 2
图 5
图 3
第7页(共22页)
2023-2024学年实验学校(中学部)七下期中数学试卷
参考答案与试题解析
一 .选择题(共10小题)
1. 下列计算正确的是( )
A.3a+2g=5g B.-(a-2)=-a-2 C.a ·a =a D.(a-1) =a -1
【解答】解:3a+2a=5a, 则A不符合题意;
-(a-2)=-a+2, 则B 不符合题意;
a ·a =a ,则C 符合题意;
(a-1) =a -2a+1, 则 D 不符合题意;
故选:C.
2. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物,却都不了解体积最小的动物, 世界上体积最小的动物要比蚂蚁小很多倍,它是被命名为H39 的原生动物,它的最长直径
也不过才0.0000003米.其中数据0.0000003用科学记数法表示为( )
A.0.3×10- B.3×10 C.3×10-7 D.3×10
【解答】解:0.0000003=3×10- .
故选: C.
3. 如图,要把河中的水引到村庄A, 小凡先作AB⊥CD, 垂足为点B, 然后沿AB开挖水
渠,就能使所开挖的水渠最短,其依据是()
D
A. 两点确定一条直线
B. 两点之间线段最短
C. 直线外一点与直线上各点连接的所有线段中,垂线段最短
D. 三角形两边之和大于第三边
【解答】解:先过点A 作AB⊥CD, 垂足为点B, 然后沿AB 开渠,能使所开的渠道最短,
这样设计的依据是垂线段最短;
故选: C.
第8页(共22页)
4. 如图,点E 在AD延长线上,下列条件中不能判定BC//AD 的是( )
A.Z1=∠2 B. ∠C=∠CDE C. ∠3=∠4
D. ∠C+∠ADC=180°
【解答】解: A、∵∠1=∠2,
∴AB/ICD, 本选项符合题意;
B、∵∠C=∠CDE,
∴BC/IAD, 本选项不合题意;
C、∵∠3=∠4,
∴BC/IAD, 本选项不合题意;
D、∵∠C+∠ADC=180°,
∴AD//BC, 本选项不符合题意.
故选: A.
5. 下列说法正确的是( )
A. 不相交的两条直线互相平行
B. 垂直于同一条直线的两条直线互相平行
C. 经过直线外一点有且只有一条直线与这条直线平行
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交
【解答】解: A. 不相交的两条直线互相平行,错误,应为:同一平面内:不相交的两条
直线互相平行.
B. 垂直于同一条直线的两条直线互相平行,错误.应为:同一平面内:垂直于同一条直
线的两条直线互相平行.
C. 经过直线外一点有且只有一条直线与这条直线平行,正确.
D. 同一平面内,两条直线的位置关系有三种:平行、垂直和相交,错误,应为:同一平
第9页(共22页)
面内,两条直线的位置关系有两种:平行、相交.
故选: C.
6. 下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( )
A.4cm B.6cm C.8cm D.10cm
【解答】解:因为弹簧伸长的长度与所挂的物体的重量成正比,设y=kx+b,
由表格得:
解得:
∴y=2x+8,
当x=0 时, y=8,
故选: C.
7. 如图,在AABC 中, BD是AABC的中线, BE是AABD的中线,若AE=3, 则AC的
长度为( )
A.3 B.6 C.9 D.12
【解答】解:∵BE 是AABD的中线,
∴AD=2AE=6,
∵BD 是AABC 的中线,
∴AC=2AD=12,
故选: D.
8. 一副直角三角板按如图所示的方式放置,点E 在 边BC 的延长线上, BE/IDF,
∠B=∠DEF=90°, 则∠CDE 的度数为( )
第10页(共22页)
A.30° B.25° C.20° D.15°
【解答】解:∵A4BC,AEFD 为直角三角板,
∴∠ACB=60°,∠EDF=45°
∵BEIIDF,
∴∠FDC=∠ACB=60°,
∴∠CDE=∠FDC-∠EDF=60°-45°=15°,
故选: D.
9.A,B 两地相距640km, 甲、乙两辆汽车从A地出发到B 地,均匀速行驶,甲出发1小 时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km), 甲行驶的时间为r(h),s 与t 的关
系如图所示,下列说法:
①甲车行驶的速度是60km/h, 乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到
①甲车行坡3动或5.甲,乙两车相距8t
其中错误的( )
A. 序号① B. 序号② C. 序号③ D. 序号④
【解答】解:①由图可得,甲车行驶的速度是60÷1=60(km/h),
∵甲先出发1h, 乙出发3h 后追上甲,
第11页(共22页)
∴3(v-60)=60,
∴Vz=80(km/h),
即乙车行驶的速度是80km/h, 故①正确;
②∵当t=1 时,乙出发,当t=4 时,乙追上甲,
:甲出发4h 后被乙追上,故②正确;
③由图可得,当乙到达B 地时,甲乙相距100km,
:.甲比乙晚到 ,故③正确;
④应该分两种情况讨论:i 乙车行驶过程中超前甲车80km,ii 乙车到达B 地,而甲车离B 地还有80km、当乙车尚在行驶中,且超前甲车80km时由图可得当60r+80=80(t-1) 时,解
得t=8;ii、 当乙车到达B 地,而甲车离B 地还有80km 时,
∵A地和B 地之间的距离是640km, 且甲车出发1小时后乙车才出发,
∴80(t-I)=640, 解得t=9, 即乙车在t=9 时到达B 地由图可得,60t+80=640 时,甲车
离B 地80km, 解得
3.甲车有数成:.甲,乙所年相an, 数3措
故选:D.
10. 如图,在AABC中 ,D 是AB的中点, E 是BC上的一点,且BE=2EC,CD 与AE相
交于点F, 若 ACEF的面积为1,则AABC的面积为( )
A.24 B.25 C.30 D.32
【解答】解:连接BF,
∵BE=2EC,
∴S mE=2Src=2,
设SpF=X
∵AD=BD
∴S DF=SABDF=X,SADC =SAaDC
第12页(共22页)
∴SDc-SAADF=SABDC-SABDF=3
∵BE =2EC
∴SE=2S
∴2x+2=2x4
∴x=3
∴Sac =SuDp+SAaDp+SAaFE+SAAE=12
故选: C,
二 .填空题(共5小题)
11. 如图,△ABC=ADEF, 则 x+y=_9
【解答】解:∵△ABC=ADEF,
∴BC=FE=5,DF=AC=4,
∴x=5,y=4,
∴x+y
=5+4
=9.
故答案为:9.
12. 一个等腰三角形的两边长分别是3cm和7cm, 则它的周长是 cm.
【解答】解:①当腰是3cm, 底边是7cm时:不满足三角形的三边关系,因此舍去.
②当底边是3cm, 腰长是7cm 时,能构成三角形,则其周长=3+7+7=17(cm).
故答案为:17.
13.已 知 2x+y-3=0, 则2° ·4*的值是8
【解答】解:由题意,得
2x+y=3.
第13页(共22页)
2'·4 =2 -2 =2 +=2 =8,
故答案为:8.
14. 如图,已知∠MAN=55°, 点B为AN上一点.用尺规按如下过程作图:以点A为圆心, 以任意长为半径画弧,交AN于点D, 交AM于点E; 以点B为圆心,以AD长为半径作弧, 交AB于点F; 以点F 为圆心,以DE长为半径作弧,交前面的弧于点G, 连接BG并延长
交AM于点C, 则∠BCM=__ 110°_.
【解答】解:由作法得∠ABC=∠A=55°,
所以∠BCM=∠A+∠ABC=55°+55°=110°,
故答案为:110°
15. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB/IDE,
∠D=70°, 则∠ACD=_20°_.
【解答】解:过点C 作CF//AB,
∵ABIIDE,
∴CF//DE,
∴∠ACF=∠BAC,∠D+∠DCF=180°,
又∠BAC=130°,∠D=70°,
∴∠ACF=130°,∠DCF=110°,
∴∠ACD=∠ACF-∠DCF=20°.
故答案为:20°.
第14页(共22页)
三 .解答题(共7小题)
16. 计算:
(2)2023 -2024×2022;
(3)(2x y) ·(-2xy)+(-2x y)÷(2x );
(4)(x+4) -(x+2)(x-5) ·
【解答】解:(1)原式=-17
(2)原式=1
(3)原式=12x y
(4)原式=11x+26
17. 先化简,再求值:[(x+y)(x-y)-(x-2y) -3y ]÷4y, 其中x=2024,y=-1.
【解答】解:原式=[x -y -(x -4xy+4y )-3y ]÷4y
=(x -y -x +4xy-4y -3y )÷4y
=(-8y +4xy)÷4y
=-2y+x,
当x=2024,y=-1 时,
原式=-2×(-1)+2024
=2+2024
=2026.
18. 看图填空:已知如图, AD⊥BC于D,EG⊥BC 于G,∠E=∠1,
求证: AD平分∠BAC.
证明:∵AD⊥BC 于D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90( 垂直的定义 ).
∴∠ADC=∠EGC (等量代换).
∴AD//EG( ).
∴∠1=∠2( ),
第15页(共22页)
∠E=∠3( ).
又∵∠E=∠1 (已知),
∴∠2=∠3(__).
∴AD平分∠BAC(_).
【解答】证明:
∵AD⊥BC于D,EG⊥BC 于G (已知),
∴∠ADC=90°,∠EGC=90° (垂直的定义),
∴∠ADC=∠EGC (等量代换),
∴AD/IEG (同位角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3 (两直线平行,同位角相等),
又∵∠E=∠1 (已知),
∴∠2=∠3(等量代换),
∴AD平分∠BAC (角平分线的定义).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,
同位角相等;等量代换;角平分线的定义.
19. 如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC 于D,AE 平分∠CAB,BD 与
AE交于点F, 求∠AFB.
【解答】解:∵∠CAB=180°-∠ABC-∠C,
而∠ABC=82°,∠C=58°,
∴∠CAB=40°,
∵AE平分∠CAB,
第16页(共22页)
∴∠DAF=20°,
∵BD⊥AC于D,
∴∠ADB=90°,
∴∠AFB=∠ADB+∠DAF=90°+20°=110°.
故答案为:110°.
20. 已知△ABC的三边长为a,b,c, 且a,b,c 都是整数.
(1)若a=2,b=5. 且c 为偶数.求AABC的周长.
(2)化简: |a-b+c|-|b-c-a|+|a+b+c|;
【解答】解:
(1)∵a=2,b=5,
∴5-2
当c=4 时, AABC的周长为a+b+c=2+5+4=11,
当c=6 时, AABC 的周长为a+b+c=2+5+6=13,
综上所述, AABC的周长为11或13.
(2)∵AABC 的三边长为a,b,c,
∴a+c>b,
:|a-b+c|-|b-c-a|+|a+b+cl
=a+c-b-(a+c-b)+a+b+c
=a+b+c;
21.【阅读理解】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如
图1可以得到(a+b) =a +2ab+b , 基于此,请解答下列问题:
【类比应用】
(1)①若xy=8,x+y=6, 则x +y 的值为
②若x(5-x)=6, 则x +(5-x) =
【迁移应用】
第17页(共22页)
(2)两块完全相同的特制直角三角板(∠AOB=∠COD=90°) 如图2所示放置,其中A,O,
D在一直线上,连接AC,BD, 若AD=14,Soc+Smop=54, 求一块三角板的面积.
图 1 图 2
【解答】解:(1)①由题意可知, x +y =(x+y) -2xy,
∵xy=8,x+y=6,
∴x +y =6 -2×8=20,
故答案为:20.
②令a=x,b=5-x,
∴a+b=5,ab=6,
∴x +(5-x) =a +b =(a+b} -2ab=5 -2×6=13,
故答案为:13.
(2)设三角板的两条直角边AO=m,BO=n, 则一块三角板的面积为 ∴m+n=14, · ,即m +n =108,
∵2mn=(m+m) -(m +n )=14 -108=88,
∴mn=44,
:一块三角板的面积是22.
22.【基础探究】
(1)如图1,AB//CD, 点E 是CD 上的点,点P 是AB 和CD 之间的一点,连接PB、PE. 若
∠B=25°,∠PEC=32°, 则∠P 的度数为_57°_ ;
(2)如图2, BE//DF,∠DBE 的平分线与∠CDF的平分线交于点G, 当∠BGD=65°时,
则∠BDC 的度数为 ;
第18页(共22页)
(3)如图3, DHIIEG, 点A 、点C 分别是DH 、EG 上的点,点B 和点F 是DH 和EG 之间的点,连接AB 、AF 、CB 、CF. 若∠B=94°,∠F=92°,AF 、CB 分别平分∠HAB、
∠GCE, 则∠BAH的度数为
【问题迁移】
(4)如图4,在△ABC中 ,BO 、CO分别平分∠ABC、∠ACB.则∠BOC与∠A的数量关
系为: ∠BOC=
【拓展深化】
如图,在AABC 中 ,D 、E 是 AB 、AC 上的点,设∠AED=m°,∠C=n°(m
为 ;
图 1
图 4
图 2
图 5
图 3
【解答】解:(1)过点P 作 PNHAB, 如图1所示:
∵AB ICD,
∴AB/IPN1ICD,
∴∠BPN=∠B,∠EPN=∠PEC,
∴∠BPN+∠EPN=∠B+∠PEC,
即∠BPE=∠B+∠PEC,
第19页(共22页)
∵∠B=25°,∠PEC=32°,
∴∠BPE=∠B+∠PEC=25°+32 =57°;
故答案为:57°
(2)设∠EBG=α,∠FDG=β, 如图2所示:
图2
∵∠DBE的平分线与∠CDF的平分线交于点G,
∴∠DBG=∠EBG=α,∠CDG=∠FDG=β,
∵BEIIDF,
由(1)可知:∠BGD=∠EBG+∠FDG=a+β,
∵∠BGD=65°,
∴a+β=65°,
∴∠DBG+∠CDG=a+β=65°,
由三角形的内角和定理得:
∠BGD+∠DGB+∠BDG=180°,
∴∠BGD+∠DGB+∠CDG+∠BDC=180°,
∴65°+65 +∠BDC=180°,
∴∠BDC=50°;
故答案为:50°.
(3)设∠HAF=α,∠GCB=β, 如图3所示:
图3
∵AF、CB 分别平分∠HAB、∠GCF,
∴∠BAF=∠HAF=a ∠BAH=2∠HAF=2a
∠GCF=2∠GCB=2β,
第20页(共22页)
∠GCF=∠GCB=β
∵DH IEG,
由(1)可知:∠B=∠HAB+∠GCB=2a+β,
∠F=∠HAF+∠GCF=α+2β,
∵∠B=94°,∠F=92°,
∴2a+β=94°,a+2β=92°,
解得:α=32°,β=30°
∴∠BAH=2a=64°,
故答案为:64°,
(4)如图1所示:
∵∠ABC+∠ACB+∠A=180°,
∴∠ABC+∠ACB=180°-∠A,
∵BO 、CO分别平分∠ABC、∠ACB,
∴ ,
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC与∠A的数量关系是:
(5)延长 DE与BC的延长线交于点F, 如图5所示:
∵∠AED=m°,
∴∠FEC=∠AED=m°,
第21页(共22页)
∵∠ACB=∠FEC+∠F,∠ACB=n°(m
∵BO、DO 分别平分∠ABC、∠BDE,
由(4)可知:
故答案为:
第22页(共22页)
同课章节目录
