2023-2024年山东省临沂市兰陵县九年级下学期期中数学试题(PDF版无答案)
文档属性
| 名称 | 2023-2024年山东省临沂市兰陵县九年级下学期期中数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 319.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 17:35:38 | ||
图片预览


文档简介
2023-2024学年度下学期阶段质量调研
九年级 数学
第 Ⅰ卷(选择题,共 30分)
一、选择题(本题共10小题,每小题3分,共30分,每小题只有一个选项符合题目要求)
1.在标准大气压下,几种物质的沸点如下表,其中沸点最低的物质是( )
物质 氮气 氧气 水 水银
沸点/℃ -196 -183 100 357
A.氮气 B.氧气 C. 水 D.水银
2.科学家可以使用冷冻电子显微镜技术以高分辨率测定溶液中的生物分子结构,使
用此技术测定某种细菌蛋白结构的分辨率达到 0.0000000018m,将 0.0000000018用科学
记数法表示为( )
A. 0.18 10 8 B.1.8 10 9 C. 0.18 10 10 D.18 10 11
3.花钿 ( diàn )是古时汉族妇女脸上用金翠珠宝制成的一种花形首饰,有红、绿、黄三种颜色,其中
以红色为最多,是唐代比较流行的一种首饰.下列四种眉心花钿图案既是轴对称图形又是中心对称图
形的是 ( )
A. B. C. D.
4.下列计算正确的是( )
A. a2 a4 a8 B. 3a3 a3 2a C.(ab2)3 a3b6 D.(a b)2 a2 b2
5.如图,是小明自制的正方形飞镖盘,若他每次投掷飞镖都能扎中飞镖盘,则小明随机
投掷一枚飞镖,恰好扎中阴影区域的概率是( )
A 1. B 1 C 1 1. . D.
2 4 6 8
6.如图,在△ABC 1中,按以下步骤作图:①分别以点 B和 C为圆心,以大于 BC的长为半径作弧,
2
两弧相交于点 M和 N;②作直线 MN交边 AB于点 E.若 AC=10,BE=8,∠B=45°,则 AB的长为
( )
A.14 B.16 C.18 D.20
7.用计算机处理数据,为了防止数据输入出错,某研究室安排两名程序操作员各输入一遍,比较两
人的输入是否一致,本次操作需输入 2640个数据,已知甲的输入速度是乙的 2倍,结果甲比乙少用 2
小时输完.这两名操作员每分钟各能输入多少个数据?设乙每分钟能输入 x个数据,根据题意得方程
正确的是( )
A 2640 2640 2640 2640 2640 2640 2640 2640. 2 B. 2 C. 2 60 D. 2 60
2x x 2x x 2x x 2x x
8.如图,AB是⊙O的直径,点 C为圆上一点且∠ABC=22°,D是劣弧 BC的中点,连接 BC,CD.则
∠BCD的度数为( )
A.22° B.32° C.34° D.68°
第 1 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
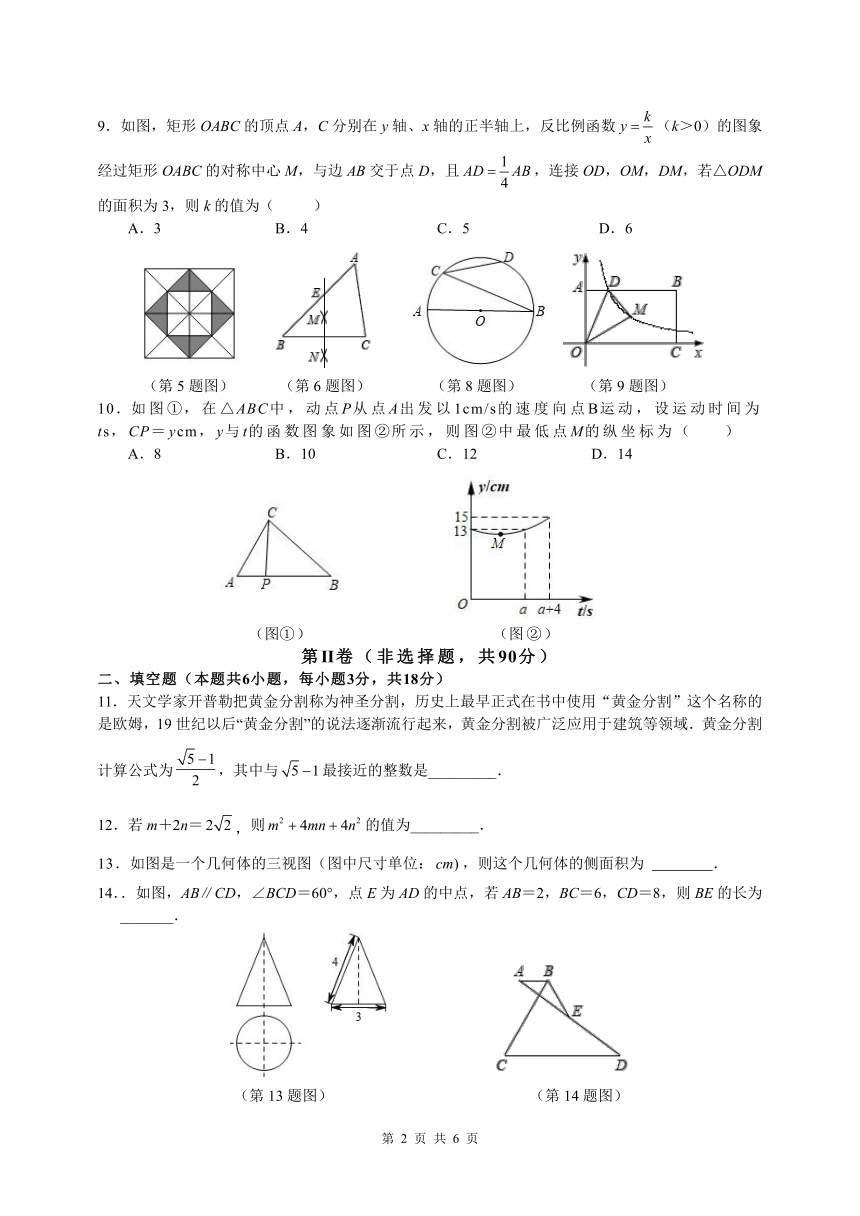
9.如图,矩形 OABC k的顶点 A,C分别在 y轴、x轴的正半轴上,反比例函数 y (k>0)的图象
x
1
经过矩形 OABC的对称中心 M,与边 AB交于点 D,且 AD AB,连接 OD,OM,DM,若△ODM
4
的面积为 3,则 k的值为( )
A.3 B.4 C.5 D.6
(第 5题图) (第 6题图) (第 8题图) (第 9题图)
10.如图①,在△ABC中,动点 P从点 A出发以 1cm/s的速度向点B运动,设运动时间为
ts,CP= ycm, y与 t的函数图象如图②所示,则图②中最低点M的纵坐标为( )
A.8 B.10 C.12 D.14
(图①) (图②)
第Ⅱ卷(非选择题,共 90分)
二、填空题(本题共6小题,每小题3分,共18分)
11.天文学家开普勒把黄金分割称为神圣分割,历史上最早正式在书中使用“黄金分割”这个名称的
是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割
5 1
计算公式为 2 ,其中与 5 1最接近的整数是_________.
12.若 m+2n= 2 2,则m
2 4mn 4n2 的值为_________.
13.如图是一个几何体的三视图(图中尺寸单位: cm),则这个几何体的侧面积为 .
14..如图,AB∥CD,∠BCD=60°,点 E为 AD的中点,若 AB=2,BC=6,CD=8,则 BE的长为
_______.
(第 13题图) (第 14题图)
第 2 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
15.已知二次函数 y ax2 x 2,当 4<x<5时,y<0,则 a的取值范围是__________.
16.观察下列等式:
第 1 1个等式: a1 2 1;1 2
第 2 1个等式: a2 3 2;2 3
第 3 1个等式: a3 2 3;3 2
1
第 4个等式: a4 5 2;2 5
按上述规律 a1 a2 a3 a2024 =_________.
三、解答题(本题共 8小题,共 72分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 8 分)
|1 2 | ( 1计算: ) 2 2cos45 3 8 ( 2024)0 .
2
18.(本小题满分 8分)
为实现绿色可持续发展,倡导低碳生活,某市的商场、超市等场所均有偿使用可
降解塑料袋.某小区为了了解每户家庭每周有偿使用可降解塑料袋的个数,随机抽取
了 20户家庭.现将这 20户家庭每周有偿使用可降解塑料袋的个数作为样本,统计结果
如下表:
个数 0 1 2 3 4
户数 8 5 3 2 2
( 1)这 20户家庭每周有偿使用可降解塑料袋个数的中位数为 ______,平均数为
______,众数为 _______;
( 2)若一个可降解塑料袋 1元,该小区有 800户家庭,请你利用样本的平均数,估
计该小区一年内(按 52周计算)有偿使用可降解塑料袋所花费的金额;
( 3)请你提出一条关于“限塑”的合理化建议.
19.(本小题满分 8 分)
在学习分式的运算时,小明提出了这样一个问题:
2x2 2x x2 x x
代数式( 2 2 ) ,它的值能等于-1吗?为什么?请你帮小明解答这个问题.x 1 x 2x 1 x 1
第 3 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
20.(本小题满分 8分)
某超市销售甲、乙两种类型的护眼台灯,已知销售 2个甲类型护眼台灯和 3个乙类
型护眼台灯可获利 29元,销售 5个甲类型护眼台灯比销售 4个乙类型护眼台灯多获利 15
元.
( 1)求销售 1个甲类型护眼台灯和 1个乙类型护眼台灯各获利多少元?
( 2)若该超市计划采购甲、乙两种类型的护眼台灯共 200个,但甲类型护眼台灯
1
的数量不能超过乙类型护眼台灯数量的 ,根据前期的销售情况,一周可售完这些台灯,问:这一
3
周要获得最大利润,应购进甲、乙两种类型的护眼台灯各多少个?
21.(本小题满分 9分)
跑步机是家庭及健身房常备的健身器材,如图① 是一款家用电动跑步机,图②
是其侧面结构示意图,已知跑步机扶手 AB和踏板 CD所在平面平行,操作面板 EA与机
架 AC之间的夹角为 120°,与扶手 AB之间的夹角为 135°,机架 AC的长为 1.3米,踏板的
厚度为 0.08米,求扶手 AB与踏板之间的距离.
(精确到 0.1米,参考数据: sin75°≈0.97, cos75°≈0.26, tan75°≈ 3.73)
第 4 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
22.(本小题满分 9 分)
如图,在 Rt△ABC中,∠C=90°,以 BC为直径的⊙O交 AB于点 D,E是 AC的中点,连接 DE.
(1)求证:DE是⊙O的切线;
(2)若 AD=16,DE=10,求 BC的长.
23.(本小题满分 10 分)
3 3
如图,抛物线 y - x2 bx c与 x轴交于 A、B两点,与 y轴交于点 C,直线 y x 3经过 A、
4 4
C两点,点 D是第二象限内抛物线上一点.
(1)求抛物线的解析式;
(2)连接 AD、CD,求△ACD面积的最大值;
(3)若点 D关于直线 BC的对称点 D′ 恰好落在直线 AC上,求点 D的坐标.
第 5 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
24.(本小题满分 12分)综合与实践
【问题情境】
已知在四边形 ABCD中,M为边 AD上一点(不与点 A,D重合),连接 BM,将△ABM
沿 BM折叠得到△NBM,点 A的对应点为点N.
【问题探究】
( 1)乐学小组的同学对正方形进行探究:若四边形 ABCD是正方形,如图①,点N落
在对角线 BD上,连接 AN并延长交CD于点G.在该图中,发现有很多与∠DGA相等的角,请
你帮他们找出与∠DGA相等的角:_____(写出一个即可);
( 2)善思小组的同学对矩形进行探究:若四边形 ABCD是矩形,如图②,点N恰好落
在 AB的垂直平分线 EF上,EF与 BM交于点G.他们发现了下列结论:①GN= 2EG;②
△GMN是等边三角形,请任意选择一个你认为正确的结论加以证明;
【深度探究】
(3)探究完后,老师又提出了如下问题,如图③,若四边形 ABCD是平行四边形,BC
= 2AB= 4,∠ABC= 60°,点N落在线段 BC上,P为AB的中点,连接DP,PN,DN,求△PND
的面积,请你完成该问题.
(图①) (图②) (图③)
第 6 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
九年级 数学
第 Ⅰ卷(选择题,共 30分)
一、选择题(本题共10小题,每小题3分,共30分,每小题只有一个选项符合题目要求)
1.在标准大气压下,几种物质的沸点如下表,其中沸点最低的物质是( )
物质 氮气 氧气 水 水银
沸点/℃ -196 -183 100 357
A.氮气 B.氧气 C. 水 D.水银
2.科学家可以使用冷冻电子显微镜技术以高分辨率测定溶液中的生物分子结构,使
用此技术测定某种细菌蛋白结构的分辨率达到 0.0000000018m,将 0.0000000018用科学
记数法表示为( )
A. 0.18 10 8 B.1.8 10 9 C. 0.18 10 10 D.18 10 11
3.花钿 ( diàn )是古时汉族妇女脸上用金翠珠宝制成的一种花形首饰,有红、绿、黄三种颜色,其中
以红色为最多,是唐代比较流行的一种首饰.下列四种眉心花钿图案既是轴对称图形又是中心对称图
形的是 ( )
A. B. C. D.
4.下列计算正确的是( )
A. a2 a4 a8 B. 3a3 a3 2a C.(ab2)3 a3b6 D.(a b)2 a2 b2
5.如图,是小明自制的正方形飞镖盘,若他每次投掷飞镖都能扎中飞镖盘,则小明随机
投掷一枚飞镖,恰好扎中阴影区域的概率是( )
A 1. B 1 C 1 1. . D.
2 4 6 8
6.如图,在△ABC 1中,按以下步骤作图:①分别以点 B和 C为圆心,以大于 BC的长为半径作弧,
2
两弧相交于点 M和 N;②作直线 MN交边 AB于点 E.若 AC=10,BE=8,∠B=45°,则 AB的长为
( )
A.14 B.16 C.18 D.20
7.用计算机处理数据,为了防止数据输入出错,某研究室安排两名程序操作员各输入一遍,比较两
人的输入是否一致,本次操作需输入 2640个数据,已知甲的输入速度是乙的 2倍,结果甲比乙少用 2
小时输完.这两名操作员每分钟各能输入多少个数据?设乙每分钟能输入 x个数据,根据题意得方程
正确的是( )
A 2640 2640 2640 2640 2640 2640 2640 2640. 2 B. 2 C. 2 60 D. 2 60
2x x 2x x 2x x 2x x
8.如图,AB是⊙O的直径,点 C为圆上一点且∠ABC=22°,D是劣弧 BC的中点,连接 BC,CD.则
∠BCD的度数为( )
A.22° B.32° C.34° D.68°
第 1 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
9.如图,矩形 OABC k的顶点 A,C分别在 y轴、x轴的正半轴上,反比例函数 y (k>0)的图象
x
1
经过矩形 OABC的对称中心 M,与边 AB交于点 D,且 AD AB,连接 OD,OM,DM,若△ODM
4
的面积为 3,则 k的值为( )
A.3 B.4 C.5 D.6
(第 5题图) (第 6题图) (第 8题图) (第 9题图)
10.如图①,在△ABC中,动点 P从点 A出发以 1cm/s的速度向点B运动,设运动时间为
ts,CP= ycm, y与 t的函数图象如图②所示,则图②中最低点M的纵坐标为( )
A.8 B.10 C.12 D.14
(图①) (图②)
第Ⅱ卷(非选择题,共 90分)
二、填空题(本题共6小题,每小题3分,共18分)
11.天文学家开普勒把黄金分割称为神圣分割,历史上最早正式在书中使用“黄金分割”这个名称的
是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割
5 1
计算公式为 2 ,其中与 5 1最接近的整数是_________.
12.若 m+2n= 2 2,则m
2 4mn 4n2 的值为_________.
13.如图是一个几何体的三视图(图中尺寸单位: cm),则这个几何体的侧面积为 .
14..如图,AB∥CD,∠BCD=60°,点 E为 AD的中点,若 AB=2,BC=6,CD=8,则 BE的长为
_______.
(第 13题图) (第 14题图)
第 2 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
15.已知二次函数 y ax2 x 2,当 4<x<5时,y<0,则 a的取值范围是__________.
16.观察下列等式:
第 1 1个等式: a1 2 1;1 2
第 2 1个等式: a2 3 2;2 3
第 3 1个等式: a3 2 3;3 2
1
第 4个等式: a4 5 2;2 5
按上述规律 a1 a2 a3 a2024 =_________.
三、解答题(本题共 8小题,共 72分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 8 分)
|1 2 | ( 1计算: ) 2 2cos45 3 8 ( 2024)0 .
2
18.(本小题满分 8分)
为实现绿色可持续发展,倡导低碳生活,某市的商场、超市等场所均有偿使用可
降解塑料袋.某小区为了了解每户家庭每周有偿使用可降解塑料袋的个数,随机抽取
了 20户家庭.现将这 20户家庭每周有偿使用可降解塑料袋的个数作为样本,统计结果
如下表:
个数 0 1 2 3 4
户数 8 5 3 2 2
( 1)这 20户家庭每周有偿使用可降解塑料袋个数的中位数为 ______,平均数为
______,众数为 _______;
( 2)若一个可降解塑料袋 1元,该小区有 800户家庭,请你利用样本的平均数,估
计该小区一年内(按 52周计算)有偿使用可降解塑料袋所花费的金额;
( 3)请你提出一条关于“限塑”的合理化建议.
19.(本小题满分 8 分)
在学习分式的运算时,小明提出了这样一个问题:
2x2 2x x2 x x
代数式( 2 2 ) ,它的值能等于-1吗?为什么?请你帮小明解答这个问题.x 1 x 2x 1 x 1
第 3 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
20.(本小题满分 8分)
某超市销售甲、乙两种类型的护眼台灯,已知销售 2个甲类型护眼台灯和 3个乙类
型护眼台灯可获利 29元,销售 5个甲类型护眼台灯比销售 4个乙类型护眼台灯多获利 15
元.
( 1)求销售 1个甲类型护眼台灯和 1个乙类型护眼台灯各获利多少元?
( 2)若该超市计划采购甲、乙两种类型的护眼台灯共 200个,但甲类型护眼台灯
1
的数量不能超过乙类型护眼台灯数量的 ,根据前期的销售情况,一周可售完这些台灯,问:这一
3
周要获得最大利润,应购进甲、乙两种类型的护眼台灯各多少个?
21.(本小题满分 9分)
跑步机是家庭及健身房常备的健身器材,如图① 是一款家用电动跑步机,图②
是其侧面结构示意图,已知跑步机扶手 AB和踏板 CD所在平面平行,操作面板 EA与机
架 AC之间的夹角为 120°,与扶手 AB之间的夹角为 135°,机架 AC的长为 1.3米,踏板的
厚度为 0.08米,求扶手 AB与踏板之间的距离.
(精确到 0.1米,参考数据: sin75°≈0.97, cos75°≈0.26, tan75°≈ 3.73)
第 4 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
22.(本小题满分 9 分)
如图,在 Rt△ABC中,∠C=90°,以 BC为直径的⊙O交 AB于点 D,E是 AC的中点,连接 DE.
(1)求证:DE是⊙O的切线;
(2)若 AD=16,DE=10,求 BC的长.
23.(本小题满分 10 分)
3 3
如图,抛物线 y - x2 bx c与 x轴交于 A、B两点,与 y轴交于点 C,直线 y x 3经过 A、
4 4
C两点,点 D是第二象限内抛物线上一点.
(1)求抛物线的解析式;
(2)连接 AD、CD,求△ACD面积的最大值;
(3)若点 D关于直线 BC的对称点 D′ 恰好落在直线 AC上,求点 D的坐标.
第 5 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
24.(本小题满分 12分)综合与实践
【问题情境】
已知在四边形 ABCD中,M为边 AD上一点(不与点 A,D重合),连接 BM,将△ABM
沿 BM折叠得到△NBM,点 A的对应点为点N.
【问题探究】
( 1)乐学小组的同学对正方形进行探究:若四边形 ABCD是正方形,如图①,点N落
在对角线 BD上,连接 AN并延长交CD于点G.在该图中,发现有很多与∠DGA相等的角,请
你帮他们找出与∠DGA相等的角:_____(写出一个即可);
( 2)善思小组的同学对矩形进行探究:若四边形 ABCD是矩形,如图②,点N恰好落
在 AB的垂直平分线 EF上,EF与 BM交于点G.他们发现了下列结论:①GN= 2EG;②
△GMN是等边三角形,请任意选择一个你认为正确的结论加以证明;
【深度探究】
(3)探究完后,老师又提出了如下问题,如图③,若四边形 ABCD是平行四边形,BC
= 2AB= 4,∠ABC= 60°,点N落在线段 BC上,P为AB的中点,连接DP,PN,DN,求△PND
的面积,请你完成该问题.
(图①) (图②) (图③)
第 6 页 共 6 页
{#{QQABLYAQogAoAIJAARgCQQWiCEAQkBEACIoGgFAAMAABSQNABAA=}#}
同课章节目录
