数学:第三章《不等式》学案(新人教b版必修5)
文档属性
| 名称 | 数学:第三章《不等式》学案(新人教b版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-06 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《不等式》复习小结 学案
一、学习目标
1.会用不等式(组)表示不等关系;
2.熟悉不等式的性质,能应用不等式的性质求解“范围问题”,会用作差法比较大小;
3.会解一元二次不等式,熟悉一元二次不等式、一元二次方程和二次函数的关系;
4.会作二元一次不等式(组)表示的平面区域,会解简单的线性规划问题;
5.明确均值不等式及其成立条件,会灵活应用均值不等式证明或求解最值。
二、重点,难点
不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用。利用不等式加法法则及乘法法则解题,求目标函数的最优解,基本不等式的应用。
三、掌握的知识点
1.本章知识结构
2、知识梳理
(一)不等式与不等关系
1、应用不等式(组)表示不等关系;
不等式的主要性质:
(1)对称性:
(2)传递性:
(3)加法法则:;
(4)乘法法则:;
(5)倒数法则:
(6)乘方法则:
(7)开方法则:
2、应用不等式的性质比较两个实数的大小;作差法
3、应用不等式性质证明
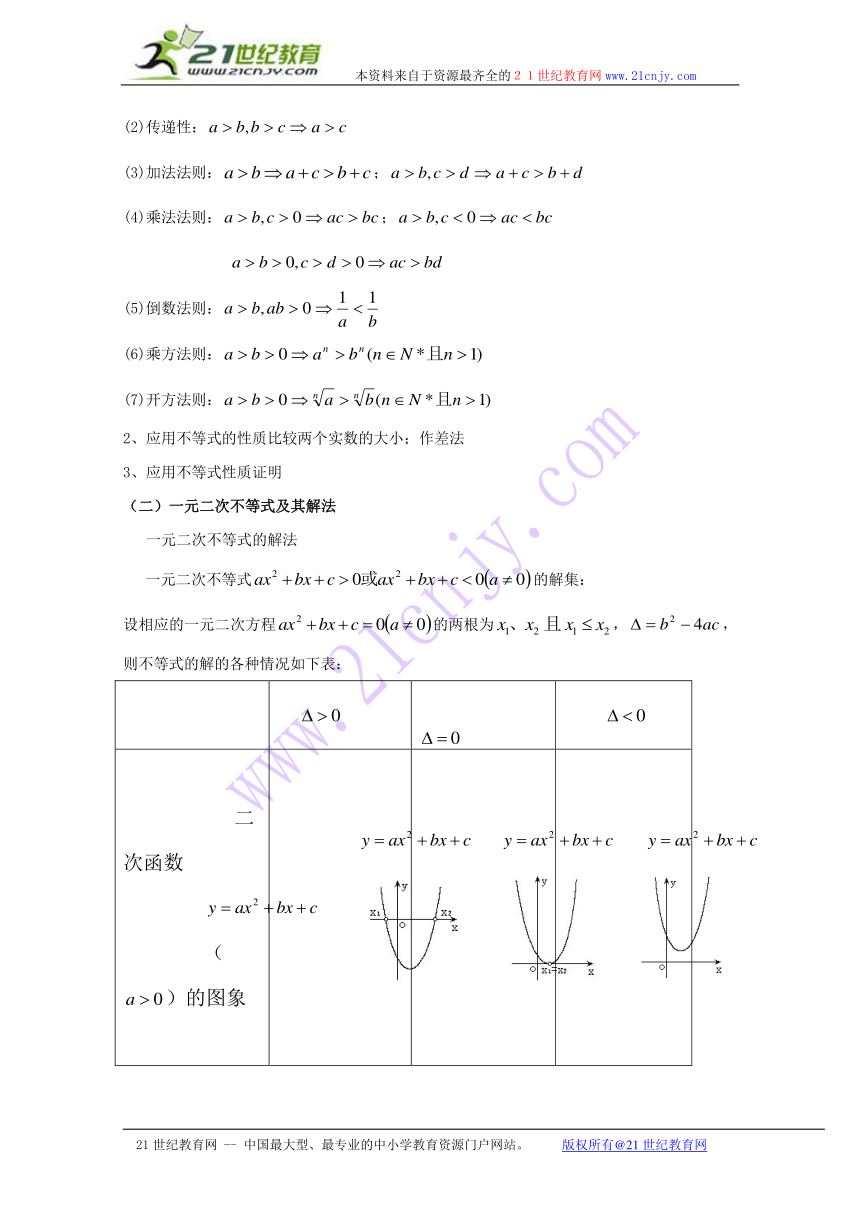
(二)一元二次不等式及其解法
一元二次不等式的解法
一元二次不等式的解集:
设相应的一元二次方程的两根为,,则不等式的解的各种情况如下表:
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
(三)线性规划
1、用二元一次不等式(组)表示平面区域
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)
2、二元一次不等式表示哪个平面区域的判断方法
由于对在直线Ax+By+C=0同一侧的所有点(),把它的坐标()代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
3、线性规划的有关概念:
①线性约束条件:在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.
③线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
④可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
4、求线性目标函数在线性约束条件下的最优解的步骤:
(1)寻找线性约束条件,线性目标函数;
(2)由二元一次不等式表示的平面区域做出可行域;
(3)在可行域内求目标函数的最优解
(四)基本不等式
1、如果a,b是正数,那么
2、基本不等式几何意义是“半径不小于半弦”
五、知识运用
1. 已知正数满足,则的最小值为 .
2. 已知且则的最小值为 .
(2)已知则的取值范围是 .
3.已知函数在点的切线方程为,若函数在上单调递增,求的取值范围.
4.对于任意,不等式恒成立,求实数的取值范围.
5.已知二次函数和一次函数,其中满足
.
(1) 求证:两函数的图象交于不同的两点;
(1) 求线段在轴上的射影的长的取值范围.
参考答案:
1.法一:
因为,
所以 .
法二:结论向条件靠,将次数升上去,方便使用条件,
=
=4(4-2+(.
又,故
2.(1)解:当且仅当时等号成立.
或解:由得,则,后略.
(2)解:由题意,
故,,
当且仅当时等号成立,.
3.解:由及得到,则.
由题设可得对恒成立.
即对恒成立 对恒成立
只需在上的最大值.对于这个最大值的计算方法可以是平均值定理法,也可以是导数法,下面我选择其中一种.
(当时等号成立)
故.
4.令,则问题转化为对于任意,恒成立,则问题
或或.
5.解: (1)由消得,由题意且.由条件不难得到,故即.可得两函数图象有两个不同的交点.
(2)设上述方程的两个根分别为,则
=
令,则原式=4(1.
由有,又,,
因此且,且.即.
所以,.
www.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《不等式》复习小结 学案
一、学习目标
1.会用不等式(组)表示不等关系;
2.熟悉不等式的性质,能应用不等式的性质求解“范围问题”,会用作差法比较大小;
3.会解一元二次不等式,熟悉一元二次不等式、一元二次方程和二次函数的关系;
4.会作二元一次不等式(组)表示的平面区域,会解简单的线性规划问题;
5.明确均值不等式及其成立条件,会灵活应用均值不等式证明或求解最值。
二、重点,难点
不等式性质的应用,一元二次不等式的解法,用二元一次不等式(组)表示平面区域,求线性目标函数在线性约束条件下的最优解,基本不等式的应用。利用不等式加法法则及乘法法则解题,求目标函数的最优解,基本不等式的应用。
三、掌握的知识点
1.本章知识结构
2、知识梳理
(一)不等式与不等关系
1、应用不等式(组)表示不等关系;
不等式的主要性质:
(1)对称性:
(2)传递性:
(3)加法法则:;
(4)乘法法则:;
(5)倒数法则:
(6)乘方法则:
(7)开方法则:
2、应用不等式的性质比较两个实数的大小;作差法
3、应用不等式性质证明
(二)一元二次不等式及其解法
一元二次不等式的解法
一元二次不等式的解集:
设相应的一元二次方程的两根为,,则不等式的解的各种情况如下表:
二次函数()的图象
一元二次方程 有两相异实根 有两相等实根 无实根
R
(三)线性规划
1、用二元一次不等式(组)表示平面区域
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)
2、二元一次不等式表示哪个平面区域的判断方法
由于对在直线Ax+By+C=0同一侧的所有点(),把它的坐标()代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点)
3、线性规划的有关概念:
①线性约束条件:在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
②线性目标函数:
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.
③线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
④可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域.
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
4、求线性目标函数在线性约束条件下的最优解的步骤:
(1)寻找线性约束条件,线性目标函数;
(2)由二元一次不等式表示的平面区域做出可行域;
(3)在可行域内求目标函数的最优解
(四)基本不等式
1、如果a,b是正数,那么
2、基本不等式几何意义是“半径不小于半弦”
五、知识运用
1. 已知正数满足,则的最小值为 .
2. 已知且则的最小值为 .
(2)已知则的取值范围是 .
3.已知函数在点的切线方程为,若函数在上单调递增,求的取值范围.
4.对于任意,不等式恒成立,求实数的取值范围.
5.已知二次函数和一次函数,其中满足
.
(1) 求证:两函数的图象交于不同的两点;
(1) 求线段在轴上的射影的长的取值范围.
参考答案:
1.法一:
因为,
所以 .
法二:结论向条件靠,将次数升上去,方便使用条件,
=
=4(4-2+(.
又,故
2.(1)解:当且仅当时等号成立.
或解:由得,则,后略.
(2)解:由题意,
故,,
当且仅当时等号成立,.
3.解:由及得到,则.
由题设可得对恒成立.
即对恒成立 对恒成立
只需在上的最大值.对于这个最大值的计算方法可以是平均值定理法,也可以是导数法,下面我选择其中一种.
(当时等号成立)
故.
4.令,则问题转化为对于任意,恒成立,则问题
或或.
5.解: (1)由消得,由题意且.由条件不难得到,故即.可得两函数图象有两个不同的交点.
(2)设上述方程的两个根分别为,则
=
令,则原式=4(1.
由有,又,,
因此且,且.即.
所以,.
www.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
