人教版八年级上册全等三角形的判定SAS(表格式)
文档属性
| 名称 | 人教版八年级上册全等三角形的判定SAS(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 09:29:36 | ||
图片预览

文档简介
课题 12.2.2全等三角形的判定(SAS)
教学目标 1.探索并正确理解三角形全等的判定方法“SAS”(重点)2.会用“SAS”证明两个三角形全等及进行简单的应用(重点)3. 了解“SSA”不能作为两个三角形全等的条件(难点)
教学重点 掌握“边角边”判定两个三角形全等的方法.
教学难点 掌握图形特征,寻找适合条件的两个三角形.
教具 三角板、圆规(多媒体课件及几何画板)
教学活动
教学步骤 师生活动 设计意图
活动一:创设情境导入新课 我国古代工匠是非常有智慧的,他们这样测量巨石的,在石头的两端各取点A 和B,在适当的位置取点C连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么? C 将课本例题进行适当变形,把教学背景从孤立的人工背景过渡到现实背景,并提出“你想知道为什么吗 ”使学生经历将实际问题转化为数学问题的建模过程,激发学生学习新知的强烈欲望.
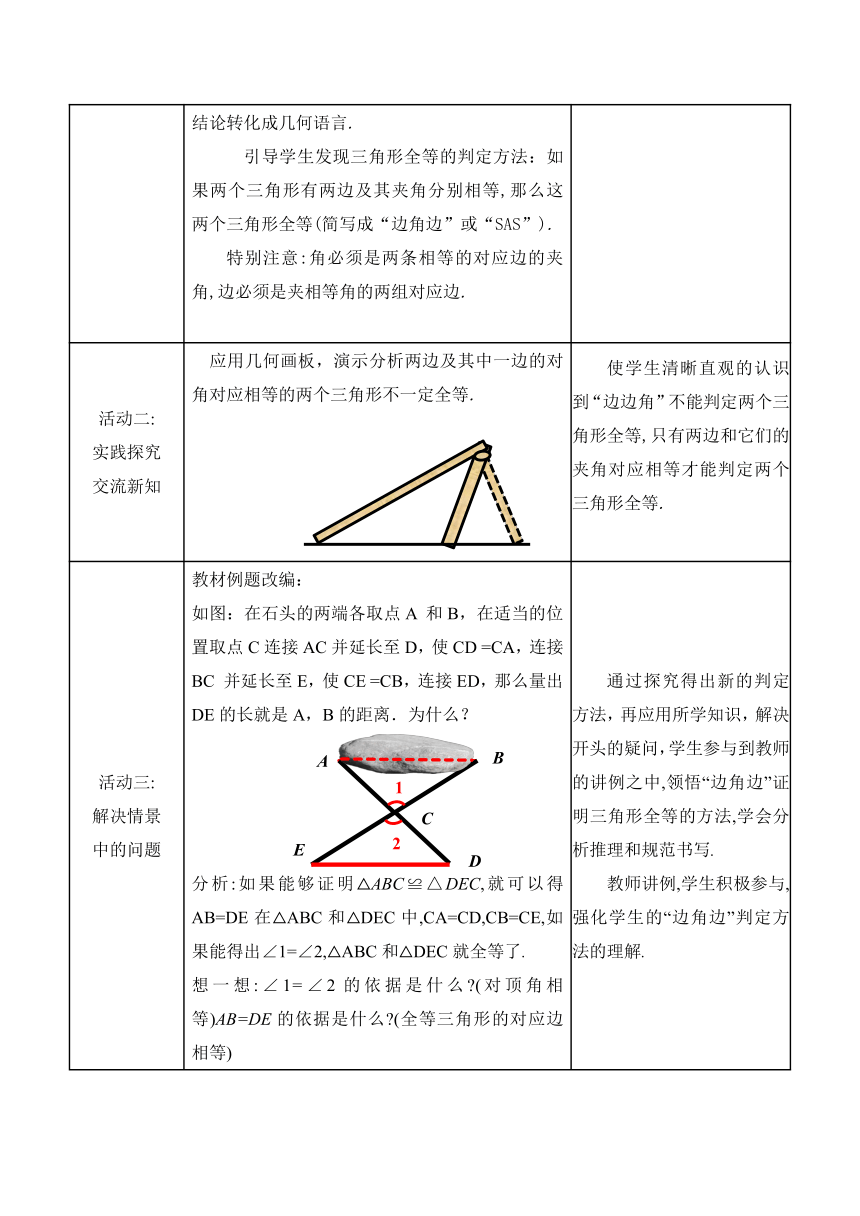
活动二:实践探究交流新知 【探究1】 请每一个同学准备两张纸,在一张纸上任意画一个△ABC,在另一张纸上尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A (即使两边和它们的夹角对应相等)将两张纸叠放在一起,两个三角形有怎样的关系?观察、概括:通过上面的画图和比较,你能用自己的语言总结出两个三角形全等的新判定方法吗 这个结论可以简单地记作什么 结合图形,请你把结论转化成几何语言.引导学生发现三角形全等的判定方法:如果两个三角形有两边及其夹角分别相等,那么这两个三角形全等(简写成“边角边”或“SAS”).特别注意:角必须是两条相等的对应边的夹角,边必须是夹相等角的两组对应边. 通过让学生画图操作,让学生发现已知两条线段和它们夹角相等,所画的三角形都是全等的.规范证明过程的书写格式.
活动二:实践探究交流新知 应用几何画板,演示分析两边及其中一边的对角对应相等的两个三角形不一定全等. 使学生清晰直观的认识到“边边角”不能判定两个三角形全等,只有两边和它们的夹角对应相等才能判定两个三角形全等.
活动三:解决情景中的问题 教材例题改编:如图:在石头的两端各取点A 和B,在适当的位置取点C连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?分析:如果能够证明△ABC≌△DEC,就可以得AB=DE在△ABC和△DEC中,CA=CD,CB=CE,如果能得出∠1=∠2,△ABC和△DEC就全等了.想一想:∠1=∠2的依据是什么 (对顶角相等)AB=DE的依据是什么 (全等三角形的对应边相等) 通过探究得出新的判定方法,再应用所学知识,解决开头的疑问,学生参与到教师的讲例之中,领悟“边角边”证明三角形全等的方法,学会分析推理和规范书写.教师讲例,学生积极参与,强化学生的“边角边”判定方法的理解.
活动四:巩固新知闯关活动 设置闯关游戏第一关:1.找出图中的全等三角形引导学生熟练SAS的应用第二关:考察共角模型及其变式2.如图,在△AEC和△ADB中,已知AE=AD,AC=AB,证明:CE=BD第二题 第三题如图所示,CD=CA,∠1=∠2,EC=BC.求证:△ABC≌△DEC.公共角经常作为证明全等的隐含条件,要提醒学生注意,另外要看清所给的等角是不是要证三角形的内角第三关:共边模型及其变式4.如图,,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________第四题 第五题5.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF. 求证:△AFD≌△CEB. 公共边也是常见的隐含条件,在证明时要留意所给的边是不是三角形的边。另外等角的补角相等,由平行推角相等也是较常用的方法,要让学生有这样的考虑。整个闯关游戏,学生运用所学由浅入深,针对不同类型,攻克了一个个难关,在提高综合运用知识的同时,也体会到较复杂图形都是由一些基本图形经过几何变换得到的。 整个闯关过程由浅入难,把不同模型进行变式,使学生发现不同并加强学生对知识的理解,借此也培养了学生仔细观察的能力,提高了学生知识的综合能力与应考能力。在闯关过程中,通过歌曲,提问,男女上黑板PK等方式,提高学生的学习兴趣,锻炼学生的表达能力,巩固深化,强化学生对“边角边”判定方法的理解,规范证明三角形全等的书写格式.
活动四:课堂总结活动五:作业布置 【课堂总结】让学生自己分享总结这节课学到了哪些知识,提高学生的总结和表达能力,引导学生建立知识网络体系。 判定:有两边及夹角对应相等的 两个三角形全等(简写成 “SAS”)应用:为证明线段和角相等提供了新的证法 注意1.已知两边,考虑找“夹角”2. 已知一角和这角的一夹边,考虑找这角的另一夹边 布置作业:每组四号到六号做课本43页复习巩固第二题每组一号到三号做课本39页练习题第二题,43页复习巩固第二题 系统归纳本节知识点,提高学生归纳问题的能力.框架图式总结,更容易形成知识网络.分层布置作业,让每个阶段的孩子都能有合适的作业写。
教学反思 【教学反思】①[授课流程反思]通过让学生在直观的操作过程中发现问题、获得新知,使学生开拓思维,发展探究新知的能力.②[讲授效果反思]教师讲解例题时要使学生明确:证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形全等来解决.学习要善于总结,在总结中提高.引导学生从知识、方法、学习习惯等多方面进行总结和反思. 回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师的教学能力.
A
B
D
E
C
A
E
D
B
1
2
边角边
教学目标 1.探索并正确理解三角形全等的判定方法“SAS”(重点)2.会用“SAS”证明两个三角形全等及进行简单的应用(重点)3. 了解“SSA”不能作为两个三角形全等的条件(难点)
教学重点 掌握“边角边”判定两个三角形全等的方法.
教学难点 掌握图形特征,寻找适合条件的两个三角形.
教具 三角板、圆规(多媒体课件及几何画板)
教学活动
教学步骤 师生活动 设计意图
活动一:创设情境导入新课 我国古代工匠是非常有智慧的,他们这样测量巨石的,在石头的两端各取点A 和B,在适当的位置取点C连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么? C 将课本例题进行适当变形,把教学背景从孤立的人工背景过渡到现实背景,并提出“你想知道为什么吗 ”使学生经历将实际问题转化为数学问题的建模过程,激发学生学习新知的强烈欲望.
活动二:实践探究交流新知 【探究1】 请每一个同学准备两张纸,在一张纸上任意画一个△ABC,在另一张纸上尺规作图画出一个△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A (即使两边和它们的夹角对应相等)将两张纸叠放在一起,两个三角形有怎样的关系?观察、概括:通过上面的画图和比较,你能用自己的语言总结出两个三角形全等的新判定方法吗 这个结论可以简单地记作什么 结合图形,请你把结论转化成几何语言.引导学生发现三角形全等的判定方法:如果两个三角形有两边及其夹角分别相等,那么这两个三角形全等(简写成“边角边”或“SAS”).特别注意:角必须是两条相等的对应边的夹角,边必须是夹相等角的两组对应边. 通过让学生画图操作,让学生发现已知两条线段和它们夹角相等,所画的三角形都是全等的.规范证明过程的书写格式.
活动二:实践探究交流新知 应用几何画板,演示分析两边及其中一边的对角对应相等的两个三角形不一定全等. 使学生清晰直观的认识到“边边角”不能判定两个三角形全等,只有两边和它们的夹角对应相等才能判定两个三角形全等.
活动三:解决情景中的问题 教材例题改编:如图:在石头的两端各取点A 和B,在适当的位置取点C连接AC并延长至D,使CD =CA,连接BC 并延长至E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?分析:如果能够证明△ABC≌△DEC,就可以得AB=DE在△ABC和△DEC中,CA=CD,CB=CE,如果能得出∠1=∠2,△ABC和△DEC就全等了.想一想:∠1=∠2的依据是什么 (对顶角相等)AB=DE的依据是什么 (全等三角形的对应边相等) 通过探究得出新的判定方法,再应用所学知识,解决开头的疑问,学生参与到教师的讲例之中,领悟“边角边”证明三角形全等的方法,学会分析推理和规范书写.教师讲例,学生积极参与,强化学生的“边角边”判定方法的理解.
活动四:巩固新知闯关活动 设置闯关游戏第一关:1.找出图中的全等三角形引导学生熟练SAS的应用第二关:考察共角模型及其变式2.如图,在△AEC和△ADB中,已知AE=AD,AC=AB,证明:CE=BD第二题 第三题如图所示,CD=CA,∠1=∠2,EC=BC.求证:△ABC≌△DEC.公共角经常作为证明全等的隐含条件,要提醒学生注意,另外要看清所给的等角是不是要证三角形的内角第三关:共边模型及其变式4.如图,,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________第四题 第五题5.如图,点E、F在AC上,AD//BC,AD=CB,AE=CF. 求证:△AFD≌△CEB. 公共边也是常见的隐含条件,在证明时要留意所给的边是不是三角形的边。另外等角的补角相等,由平行推角相等也是较常用的方法,要让学生有这样的考虑。整个闯关游戏,学生运用所学由浅入深,针对不同类型,攻克了一个个难关,在提高综合运用知识的同时,也体会到较复杂图形都是由一些基本图形经过几何变换得到的。 整个闯关过程由浅入难,把不同模型进行变式,使学生发现不同并加强学生对知识的理解,借此也培养了学生仔细观察的能力,提高了学生知识的综合能力与应考能力。在闯关过程中,通过歌曲,提问,男女上黑板PK等方式,提高学生的学习兴趣,锻炼学生的表达能力,巩固深化,强化学生对“边角边”判定方法的理解,规范证明三角形全等的书写格式.
活动四:课堂总结活动五:作业布置 【课堂总结】让学生自己分享总结这节课学到了哪些知识,提高学生的总结和表达能力,引导学生建立知识网络体系。 判定:有两边及夹角对应相等的 两个三角形全等(简写成 “SAS”)应用:为证明线段和角相等提供了新的证法 注意1.已知两边,考虑找“夹角”2. 已知一角和这角的一夹边,考虑找这角的另一夹边 布置作业:每组四号到六号做课本43页复习巩固第二题每组一号到三号做课本39页练习题第二题,43页复习巩固第二题 系统归纳本节知识点,提高学生归纳问题的能力.框架图式总结,更容易形成知识网络.分层布置作业,让每个阶段的孩子都能有合适的作业写。
教学反思 【教学反思】①[授课流程反思]通过让学生在直观的操作过程中发现问题、获得新知,使学生开拓思维,发展探究新知的能力.②[讲授效果反思]教师讲解例题时要使学生明确:证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形全等来解决.学习要善于总结,在总结中提高.引导学生从知识、方法、学习习惯等多方面进行总结和反思. 回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师的教学能力.
A
B
D
E
C
A
E
D
B
1
2
边角边
