5.2 探索轴对称的性质 课件(共17张PPT)2023-2024学年度北师大版数学七年级下册
文档属性
| 名称 | 5.2 探索轴对称的性质 课件(共17张PPT)2023-2024学年度北师大版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 09:48:58 | ||
图片预览



文档简介
(共17张PPT)
第五章 生活中的轴对称
2 探索轴对称的性质
轴对称图形:如果一个图形沿某条直线对折后,直线两
旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
轴对称:对于两个图形,把一个图形沿着某一条直线对
折,如果它能够与另一个图形完全重合,那么就说这
两个图形成轴对称。
这条直线就是对称轴
课堂导入
温故
知新
思考:
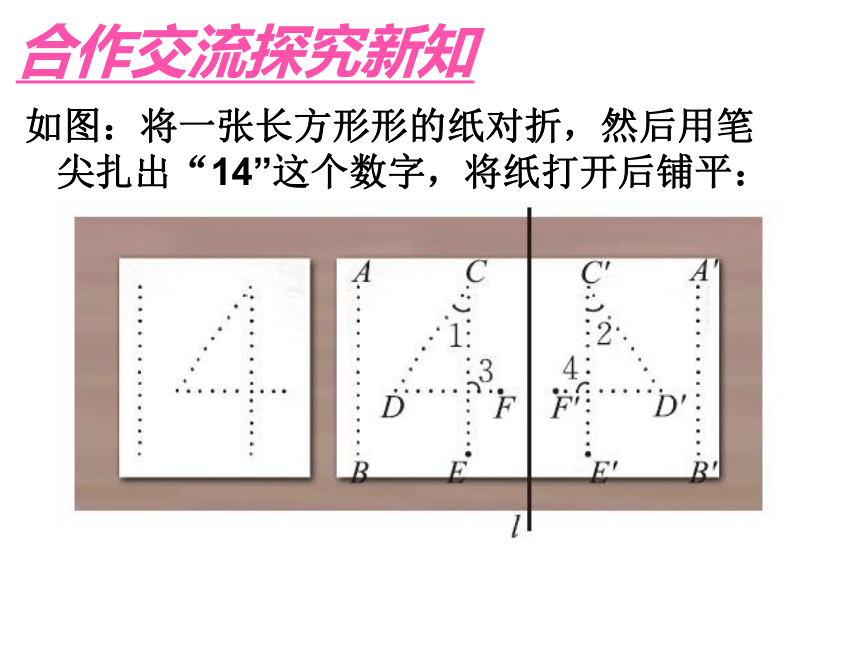
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
合作交流探究新知
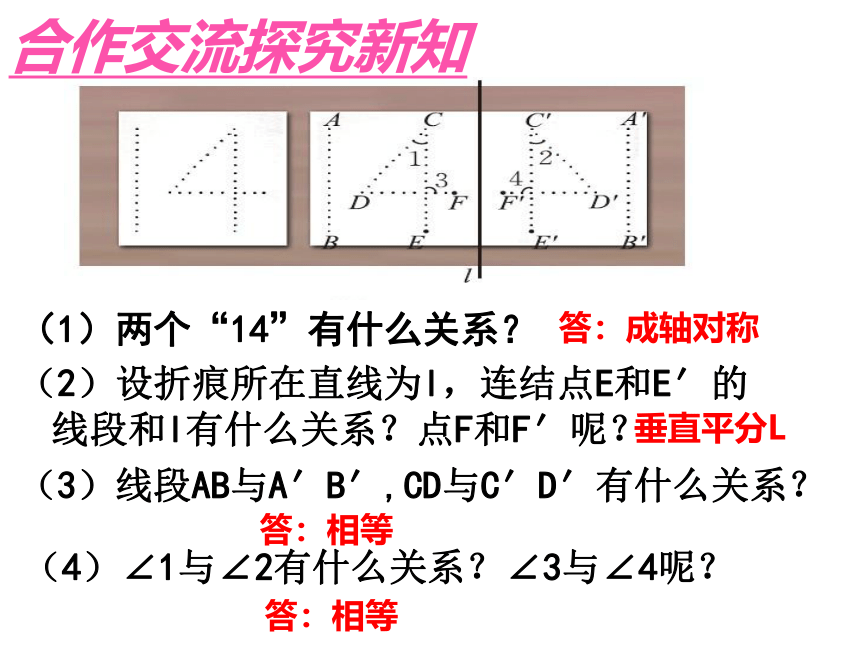
(1)两个“14”有什么关系?
(2)设折痕所在直线为l,连结点E和E′的线段和l有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
答:成轴对称
垂直平分L
答:相等
答:相等
合作交流探究新知
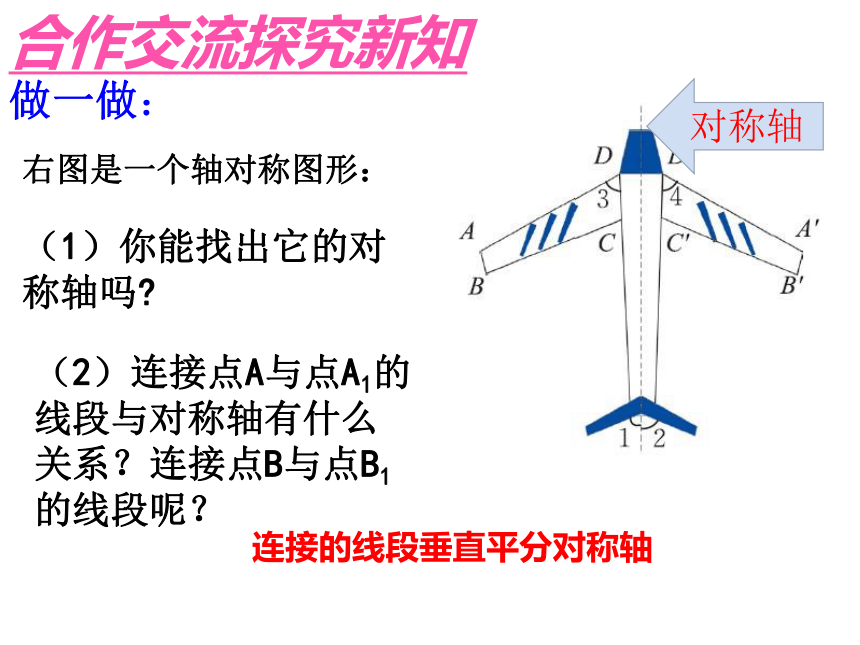
做一做:
右图是一个轴对称图形:
(1)你能找出它的对称轴吗
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
A
对称轴
连接的线段垂直平分对称轴
合作交流探究新知
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系 ∠ 3与∠4呢?说说你的理由?
答:相等,因为它们关于
对称轴对称重合
答:相等,因为它们关于
对称轴对称重合
合作交流探究新知
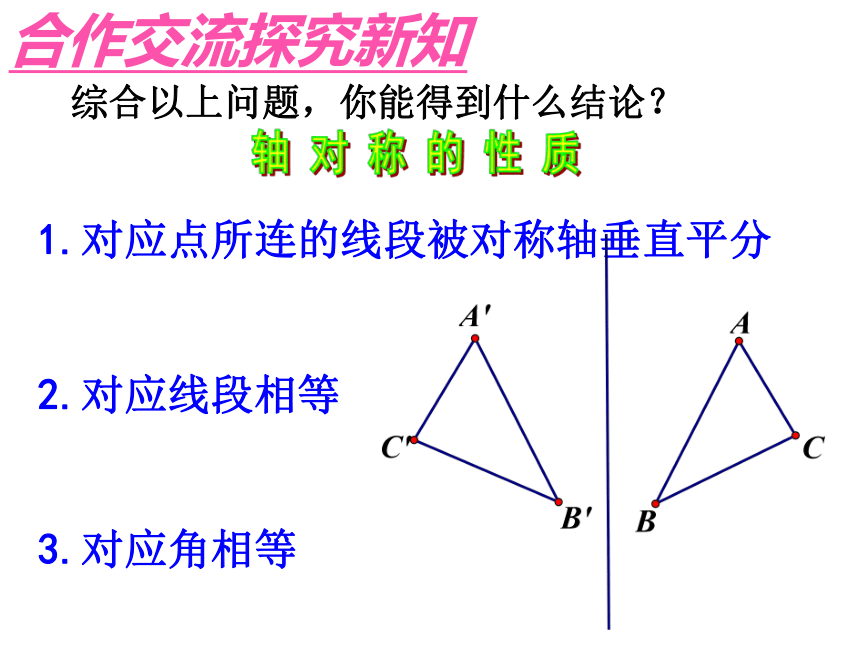
综合以上问题,你能得到什么结论?
轴 对 称 的 性 质
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等
3.对应角相等
合作交流探究新知
图5-6是一个图案的一半,虚线是图形的对称轴,画出这个图案的另一半。
合作交流探究新知
做一做:
例:如图所示,AD为 △ABC 的高,∠B= 2∠C ,借助于轴对称的性质想一想:CD与AB+BD相等吗?请说明你的理由.
范例研讨运用新知
答:相等,理由如下:
在DC上截取DE使DE=DB,连接AE
∵AD⊥BE且DB=DE ∴B、E关于AD对称
∴△ABD与△AED关于直线AD对称
∴ △ABD ≌ △AED ∴AB=AE,∠AED= ∠B
又∵ ∠B=2 ∠C ∴ ∠AED= 2 ∠C
而∠AED= ∠C + ∠CAE ∴ ∠CAE = ∠ C
∴AE=CE ∴AB=CE 故AB+BD=DE+EC
即:AB+BD=CD
范例研讨运用新知
1. 如果两个图形关于某条直线对称,那么对应点所连的线段被 垂直平分。
2. 下图是轴对称图形,相等的线段是 式, 相等的角 。
对称轴
AB=CD,BE=CE
∠B=∠C
A
B
C
D
E
反馈练习巩固新知
你一定能行!
认真做一做:
3.两个图形关于某直线对称,对称点一定 ( )
A.这直线的两旁 B.这直线的同旁
C.这直线上 D.这直线两旁或这直线上
D
4.轴对称图形沿对称轴对折后,对称轴两旁的
部分( )
A.完全重合 B.不完全重合 C.两者都有
A
认真做一做:
反馈练习巩固新知
5. 若直角三角形是轴对称图形,则它的三个内角的度数分别为 。
45°,45°,90°
反馈练习巩固新知
6、某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B。为了节约资金,使修建的水渠最短,应将缺口P修建在哪里 请你利用所学知识解决这一问题,并用红色线段画出水渠。
A
B
P
M
N
A
B
M
A1
反馈练习巩固新知
通过这堂课的学习,你掌握了轴对称的哪些性质?
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
课堂小结布置作业
小结:
课堂小结布置作业
布置作业
课本122-123页 第2、3题
谢
谢
第五章 生活中的轴对称
2 探索轴对称的性质
轴对称图形:如果一个图形沿某条直线对折后,直线两
旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
轴对称:对于两个图形,把一个图形沿着某一条直线对
折,如果它能够与另一个图形完全重合,那么就说这
两个图形成轴对称。
这条直线就是对称轴
课堂导入
温故
知新
思考:
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
合作交流探究新知
(1)两个“14”有什么关系?
(2)设折痕所在直线为l,连结点E和E′的线段和l有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
答:成轴对称
垂直平分L
答:相等
答:相等
合作交流探究新知
做一做:
右图是一个轴对称图形:
(1)你能找出它的对称轴吗
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
A
对称轴
连接的线段垂直平分对称轴
合作交流探究新知
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系 ∠ 3与∠4呢?说说你的理由?
答:相等,因为它们关于
对称轴对称重合
答:相等,因为它们关于
对称轴对称重合
合作交流探究新知
综合以上问题,你能得到什么结论?
轴 对 称 的 性 质
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等
3.对应角相等
合作交流探究新知
图5-6是一个图案的一半,虚线是图形的对称轴,画出这个图案的另一半。
合作交流探究新知
做一做:
例:如图所示,AD为 △ABC 的高,∠B= 2∠C ,借助于轴对称的性质想一想:CD与AB+BD相等吗?请说明你的理由.
范例研讨运用新知
答:相等,理由如下:
在DC上截取DE使DE=DB,连接AE
∵AD⊥BE且DB=DE ∴B、E关于AD对称
∴△ABD与△AED关于直线AD对称
∴ △ABD ≌ △AED ∴AB=AE,∠AED= ∠B
又∵ ∠B=2 ∠C ∴ ∠AED= 2 ∠C
而∠AED= ∠C + ∠CAE ∴ ∠CAE = ∠ C
∴AE=CE ∴AB=CE 故AB+BD=DE+EC
即:AB+BD=CD
范例研讨运用新知
1. 如果两个图形关于某条直线对称,那么对应点所连的线段被 垂直平分。
2. 下图是轴对称图形,相等的线段是 式, 相等的角 。
对称轴
AB=CD,BE=CE
∠B=∠C
A
B
C
D
E
反馈练习巩固新知
你一定能行!
认真做一做:
3.两个图形关于某直线对称,对称点一定 ( )
A.这直线的两旁 B.这直线的同旁
C.这直线上 D.这直线两旁或这直线上
D
4.轴对称图形沿对称轴对折后,对称轴两旁的
部分( )
A.完全重合 B.不完全重合 C.两者都有
A
认真做一做:
反馈练习巩固新知
5. 若直角三角形是轴对称图形,则它的三个内角的度数分别为 。
45°,45°,90°
反馈练习巩固新知
6、某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B。为了节约资金,使修建的水渠最短,应将缺口P修建在哪里 请你利用所学知识解决这一问题,并用红色线段画出水渠。
A
B
P
M
N
A
B
M
A1
反馈练习巩固新知
通过这堂课的学习,你掌握了轴对称的哪些性质?
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
课堂小结布置作业
小结:
课堂小结布置作业
布置作业
课本122-123页 第2、3题
谢
谢
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
