人教版五年级数学上册组合图形的面积课件(共33张PPT)
文档属性
| 名称 | 人教版五年级数学上册组合图形的面积课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-26 12:13:44 | ||
图片预览






文档简介
(共33张PPT)
组合图形的面积
新人教版五年级数学上册
课前热热身
学 习 新 知
分 层 训 练
正方形
梯 形
三角形
长方形
平行四边形
我们都学过哪些平面图形?
课前热热身
它们的面积是怎样计算的呢?
长 方 形 的 面 积 =
正 方 形 的 面 积 =
平行四边形的面积=
三 角 形 的 面 积 =
梯 形 的 面 积 =
长 ×宽 S=ab
边长×边长 S=a×a
底×高 S=ah
底×高÷2 S=ah÷2
(上底+下底)×高÷2 S=(a+b)h÷2
返回目录
学 习 新 知
下面这些组合图形里有哪些学过的图形?
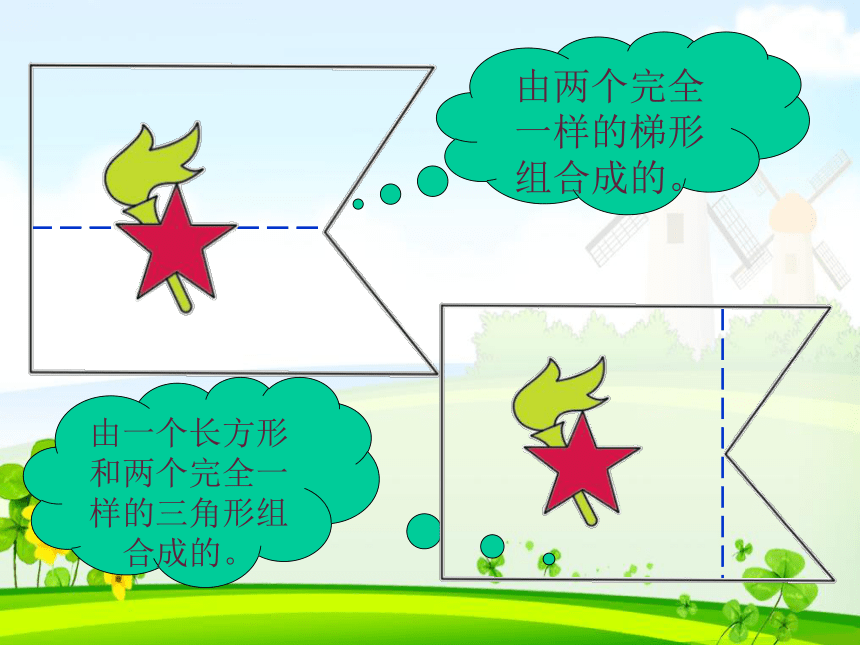
由两个完全一样的梯形组合成的。
由一个长方形和两个完全一样的三角形组合成的。
由三角形、正方形和长方形组合成的。
由四个三角形组合成的。
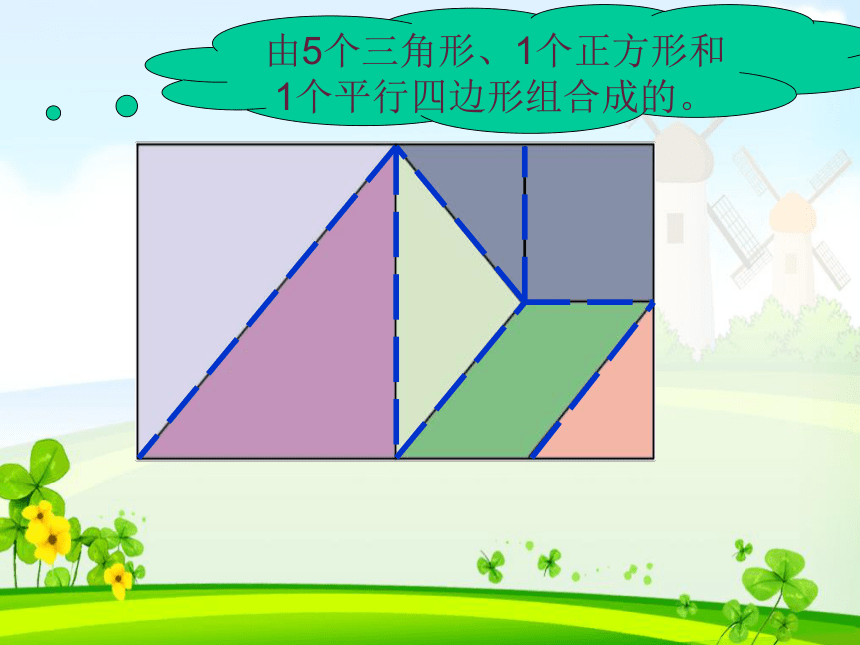
由5个三角形、1个正方形和1个平行四边形组合成的。
由几个简单的图形拼出来的图形,我们把它们叫做组合图形。
生活中有哪些地方有组合图形?
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
你能想出几种方法?
这就是我们刚才看到的一间房子的侧面墙,它的面积有多大呢?
请同学们小组合作,利用手中的答题卡,先讨论方法,并画一画,再说一说这个图形的面积该怎样求
分割法
添补法
方法一
方法二
方法三
方法一:三角形的面积+正方形的面积
方法二:直角梯形的面积×2
5+2=7(m) 5÷2=2.5(m)
(5+7)×2.5÷2×2
=12×2.5÷2×2
=30 (m2)
5×2÷2+5×5
=5+25
=30(m2)
方法三:长方形的面积 — 小三角形的面积×2
7×5-2×2.5÷2×2
=35-5
=30 (m2)
图中每个小方格的面积是1平方厘米,请你估计这片叶子的面积。
1厘米
方法一
数格子。
把树叶放到每个方格面积是1平方厘米的格子图中,不足一格按半格计算。
树叶大约有30个1平方厘米的小方格那么大
方法二
把不规则图形看作规则图形计算
树叶的形状行四边形
S=ah
=5×6
=30(平方厘米)
答案不唯一。
小 结
计算组合图形的面积时,要根据图形本身的特点,灵活地选择计算方法(分割法或添补法)。
谁来说一说,这节课你都学习了哪些知识?有什么收获?
返回目录
分 层 训 练
夯实基础
提升培优
思维创新
返回目录
1.(基础题)下面的图形是由哪些简单图
形组成的?画一画。
夯实基础
答案不唯一。
2.(重点题)计算下列组合图形的面积。
(单位:cm)
12×13
19×31
+
=156 + 247
=745(cm2)
12
13
19
31
夯实基础
(1)
2.(重点题)计算下列组合图形的面积。
(单位:cm)
21
20
52
52×21÷2
52×20
+
=546+1040
=1586(cm2)
(4+11)×5÷2
8×4
+
=37.5+32
=69.5(cm2)
11
8
4
13
13- 8=5(㎝)
夯实基础
(2)
(3)
3、(重点题)估算下面图形的面积。(每个小
方格的面积表示1平方厘米)
(1)小华出生时,脚印的面积约是多少?
小华出生时,脚印的面积约是18 平方厘米。
(答案不唯一)
3、(重点题)估算下面图形的面积。(每个小
方格的面积表示1平方厘米)
(2)小华2岁时,脚印的面积约是多少?
小华2岁时,脚印的面积约是40平方厘米。(答案不唯一)
(3)估计自己脚印的面积。
4.(难点题)用两种不同的方法计算下面
图形的面积。(单位:cm)
20
18
6
10
2
方法一
(10+20)×2÷2=30(㎝ )
(18-2+18)×6÷2=102(㎝ )
30+102=132(㎝ )
方法二
(10+20-6)×2÷2=24(㎝ )
6×18=108(㎝ )
24+108=132(㎝ )
提升培优
20
10
16
5.(易错题)求下面图形的面积。
(单位:cm)
12
(10+16) ×12÷2
20×(16-10) ÷2
+
=156+60
=216(cm2)
提升培优
6.(竞赛题)求下图中阴影部分的面积。
20米
20米
10米
10米
10 ×10÷2=50(平方米)
(20-10)×20÷2=100(平方米)
100+50=150(平方米)
思维创新
把阴影部分分割成两个三角形。
祝同学们学习愉快
组合图形的面积
新人教版五年级数学上册
课前热热身
学 习 新 知
分 层 训 练
正方形
梯 形
三角形
长方形
平行四边形
我们都学过哪些平面图形?
课前热热身
它们的面积是怎样计算的呢?
长 方 形 的 面 积 =
正 方 形 的 面 积 =
平行四边形的面积=
三 角 形 的 面 积 =
梯 形 的 面 积 =
长 ×宽 S=ab
边长×边长 S=a×a
底×高 S=ah
底×高÷2 S=ah÷2
(上底+下底)×高÷2 S=(a+b)h÷2
返回目录
学 习 新 知
下面这些组合图形里有哪些学过的图形?
由两个完全一样的梯形组合成的。
由一个长方形和两个完全一样的三角形组合成的。
由三角形、正方形和长方形组合成的。
由四个三角形组合成的。
由5个三角形、1个正方形和1个平行四边形组合成的。
由几个简单的图形拼出来的图形,我们把它们叫做组合图形。
生活中有哪些地方有组合图形?
右图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
你能想出几种方法?
这就是我们刚才看到的一间房子的侧面墙,它的面积有多大呢?
请同学们小组合作,利用手中的答题卡,先讨论方法,并画一画,再说一说这个图形的面积该怎样求
分割法
添补法
方法一
方法二
方法三
方法一:三角形的面积+正方形的面积
方法二:直角梯形的面积×2
5+2=7(m) 5÷2=2.5(m)
(5+7)×2.5÷2×2
=12×2.5÷2×2
=30 (m2)
5×2÷2+5×5
=5+25
=30(m2)
方法三:长方形的面积 — 小三角形的面积×2
7×5-2×2.5÷2×2
=35-5
=30 (m2)
图中每个小方格的面积是1平方厘米,请你估计这片叶子的面积。
1厘米
方法一
数格子。
把树叶放到每个方格面积是1平方厘米的格子图中,不足一格按半格计算。
树叶大约有30个1平方厘米的小方格那么大
方法二
把不规则图形看作规则图形计算
树叶的形状行四边形
S=ah
=5×6
=30(平方厘米)
答案不唯一。
小 结
计算组合图形的面积时,要根据图形本身的特点,灵活地选择计算方法(分割法或添补法)。
谁来说一说,这节课你都学习了哪些知识?有什么收获?
返回目录
分 层 训 练
夯实基础
提升培优
思维创新
返回目录
1.(基础题)下面的图形是由哪些简单图
形组成的?画一画。
夯实基础
答案不唯一。
2.(重点题)计算下列组合图形的面积。
(单位:cm)
12×13
19×31
+
=156 + 247
=745(cm2)
12
13
19
31
夯实基础
(1)
2.(重点题)计算下列组合图形的面积。
(单位:cm)
21
20
52
52×21÷2
52×20
+
=546+1040
=1586(cm2)
(4+11)×5÷2
8×4
+
=37.5+32
=69.5(cm2)
11
8
4
13
13- 8=5(㎝)
夯实基础
(2)
(3)
3、(重点题)估算下面图形的面积。(每个小
方格的面积表示1平方厘米)
(1)小华出生时,脚印的面积约是多少?
小华出生时,脚印的面积约是18 平方厘米。
(答案不唯一)
3、(重点题)估算下面图形的面积。(每个小
方格的面积表示1平方厘米)
(2)小华2岁时,脚印的面积约是多少?
小华2岁时,脚印的面积约是40平方厘米。(答案不唯一)
(3)估计自己脚印的面积。
4.(难点题)用两种不同的方法计算下面
图形的面积。(单位:cm)
20
18
6
10
2
方法一
(10+20)×2÷2=30(㎝ )
(18-2+18)×6÷2=102(㎝ )
30+102=132(㎝ )
方法二
(10+20-6)×2÷2=24(㎝ )
6×18=108(㎝ )
24+108=132(㎝ )
提升培优
20
10
16
5.(易错题)求下面图形的面积。
(单位:cm)
12
(10+16) ×12÷2
20×(16-10) ÷2
+
=156+60
=216(cm2)
提升培优
6.(竞赛题)求下图中阴影部分的面积。
20米
20米
10米
10米
10 ×10÷2=50(平方米)
(20-10)×20÷2=100(平方米)
100+50=150(平方米)
思维创新
把阴影部分分割成两个三角形。
祝同学们学习愉快
