数学:1.2《空间几何体的三视图》学案(新人教版a必修2)
文档属性
| 名称 | 数学:1.2《空间几何体的三视图》学案(新人教版a必修2) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-07 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.2 空间几何体的三视图
一、三维目标
1.了解平行投影与中心投影的概念和简单性质。
2 理解三视图的含义,能画出简单几何体的三视图,掌握画法规则。
3.能根据三视图,运用空间想象能力,识别并说出它所表示的空间图形。
二、导学提纲
1.平行投影的投影线互相平行,而中心投影的投影线 。在平行投影中,投影线 时,叫做正投影,否则叫做 。21世纪教育网
2.空间几何体的三视图是指 、 、 。
3.三视图的排列规则是 放在正视图的下方,长度与正视图一样, 放在正视图一样,宽度与俯视图的宽度一样。
4.三视图的正视图、俯视图、侧视图分别是从 、 、 观察同一个几何体,画出的空间几何体的图形。
5.三视图对于认识空间几何体有何作用?你有何体会?
三小试牛刀
1.下列命题正确的是( )
A.一个点在一个平面内的投影仍是一个点
B.一条线段在一个平面内的投影仍是线段
C.一条直线在一个平面内的投影仍是一条直线
D.一个三角形在一个平面内的投影仍是三角形
2.一个圆柱的三视图中,一定没有的图形是( )
A.正方形 B.长方形 C.三角形 D.圆
3.一个正方形的平行投影的形状可能是 。
4.一个几何体的三视图如下图。
则这个几何体的名称是 。
四、典例剖析
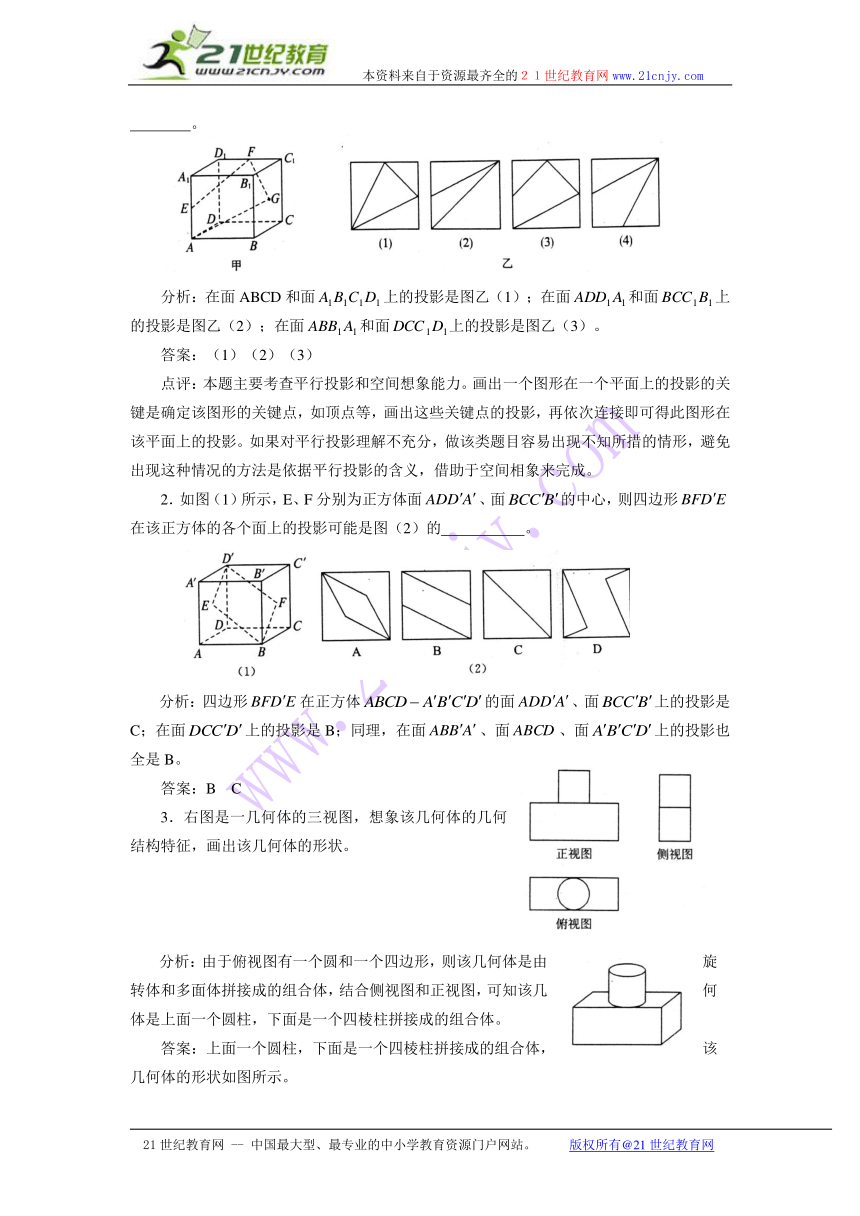
1.如图甲所示,在正方体中,E、F分别是、的中点,G是正方形的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的 。
分析:在面ABCD和面上的投影是图乙(1);在面和面上的投影是图乙(2);在面和面上的投影是图乙(3)。
答案:(1)(2)(3)
点评:本题主要考查平行投影和空间想象能力。画出一个图形在一个平面上的投影的关键是确定该图形的关键点,如顶点等,画出这些关键点的投影,再依次连接即可得此图形在该平面上的投影。如果对平行投影理解不充分,做该类题目容易出现不知所措的情形,避免出现这种情况的方法是依据平行投影的含义,借助于空间相象来完成。
2.如图(1)所示,E、F分别为正方体面、面的中心,则四边形在该正方体的各个面上的投影可能是图(2)的 。
分析:四边形在正方体的面、面上的投影是C;在面上的投影是B;同理,在面、面、面上的投影也全是B。
答案:B C
3.右图是一几何体的三视图,想象该几何体的几何结构特征,画出该几何体的形状。
分析:由于俯视图有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体,结合侧视图和正视图,可知该几何体是上面一个圆柱,下面是一个四棱柱拼接成的组合体。
答案:上面一个圆柱,下面是一个四棱柱拼接成的组合体,该几何体的形状如图所示。
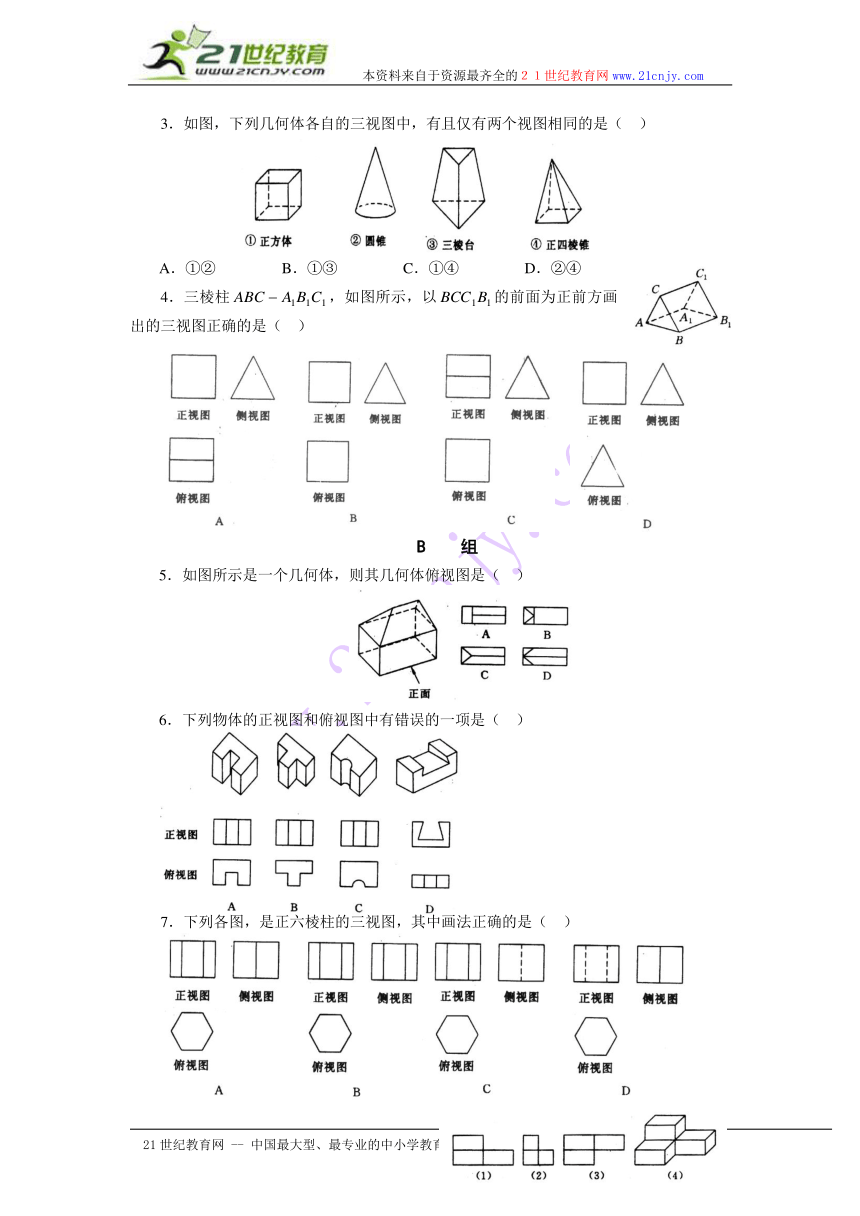
4.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
分析:正方体的三视图都是正方形,所以①不符合题意,排除A、B、C。
答案:D
点评:虽然三视图的画法比较繁琐,但是三视图是考查空间想象能力的重要形式,因此是新课标高考的必考内容之一,足够的空间想象能力才能保证顺利解决三视图问题。
5.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥
C.四棱台 D.三棱台
分析:由所给三视图可以判定对应的几何体是四棱锥。
答案:B
6.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )
A.8 B.7 C.6 D.5
分析:由正视图和侧视图可知,该几何体有两层小正方体拼接成,由俯视图,可知最下层有5个小正方体,由侧视图可知上层仅有一个正方体,则共有6个小正方体。
答案:C
空间几何体的三视图
No.038 班级 姓名 学号 成绩
A 组
1.直线的平行投影可能是( )
A.点 B.线段 C.射线 D.曲线
2.如图所示,空心圆柱体的正视图是( )
3.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
4.三棱柱,如图所示,以的前面为正前方画出的三视图正确的是( )
B 组
5.如图所示是一个几何体,则其几何体俯视图是( )
6.下列物体的正视图和俯视图中有错误的一项是( )
7.下列各图,是正六棱柱的三视图,其中画法正确的是( )
8.如图,图(1)、(2)、(3)是图(4)所表示的几何体的三视图,其中图(1)是 ,图(2)是 ,图(3)是 。(说出视图名称)
C 组
9.根据图中的三视图想象物体原形,并分别画出物体的实物图。
10.如图,E、F分别是正方体的面和面的中心,则四边形在该正方体的面上的正投影(投射线垂直于投影面的投影)可能是图中 (把所有可能图形的序号都填上)。
1.2 空间几何体的直观图
一、三维目标
1.体会平面图形和空间图形的直观图的含义。
2.结合画直观图的实例,掌握直观图的斜二测画法及步骤。
3.会用斜二测画法画水平放置的平面图形的直观图。
4.会用斜二测画法画柱、锥、台、球及其简单组合体等空间图形的直观图。
二、导学提纲
1.表示空间图形的 ,叫做空间图形的直观图。
2.用斜二测画法画空间图形的直观图时,图形中平行于轴、轴或轴的线段,在直观图中分别画成 于轴、轴或轴的线段。平行于轴和轴的线段,在直观图中长度 ;平行于轴的线段,长度变为原来的 。
3.斜二测画法是一种特殊的 投影画法。
4.用斜二测画法画水平放置的平面图形时会改变两线段的关系吗?
三、小试牛刀
1.利用斜二测画法叙述正确的是( )
A.正三角形的直观图是正三角形 B.平行四边形的直观图是平行四边形
C.矩形的直观图是矩形 D.圆的直观图一定是圆
2.下列结论正确的是( )
A.相等的线段在直观图中仍然相等
B.若两条线段平行,则在直观图中对应的两条线段仍然平行
C.两个全等三角形的直观图一定也全等
D.两个图形的直观图是全等的三角形,则这两个图形是全等三角形
3.直角坐标系中一个平面图形上的一条线段AB的实际长度为4cm,若AB//轴,则画出直观图后对应的线段 ,若轴,则画出直观图后对应的线段= 。
4.水平放置的的斜二测直观图如图所示,已知,则AB边上的中线的实际长度为 。
四、典例剖析
1.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积是( )
A.16 B.64 C.16或64 D.都不对
分析:根据直观图的画法,平行于轴的线段长度不变,平行于轴的线段变为原来的一半,于是长为4的边如果平行于轴,则正方形边长为4,面积为16,边长为4的边如果平行于轴,则正方形边长为8,面积是64。
答案:C
2.利用斜二测画法画直观图时:
①三角形的直观图是三角形; ②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形; ④菱形的直观图是菱形。
以上结论中,正确的是 。
分析:斜二测画法保持平行性和相交性不变,即平行直线的直观图还是平行直线,相交直线的直观图还是相交直线,故①②正确;但是斜二测画法中平行于轴的线段,在直观图中长度为原来的一半,则正方形的直观图不是正方形,菱形的直观图不是菱形,所以③④错。
答案:①②
3.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是( )
A. B. C. D.都不对
分析:根据斜二测画法的规则,正三角形的边长是原三角形的底边长,原三角形的高是正三角形高的倍,而正三角形的高是,所以原三角形的高为,于是其面积为
答案:A
4.一个水平放置的平面图形的直观图是一个底角为,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
A. B. C. D.
分析:平面图形是上底长为1,下底长为,高为2的直角梯形。计算得面积为
答案:D
5.斜二测画法中,位于平面直角坐标系中的点的直观图中对应点是,则点的找法是 。
分析:在轴的正方向上取点,使,在轴上取点,使,过和分别作平行于轴和轴的直线的交点就是
答案:在中,过点和轴平行的直线与过和轴平行的直线的交点即是。
6.根据图中所示物体的三视图(阴影部分为空洞)描绘出物体的大致形状。
分析:根据该物体的三视图可以判断该物体的外轮廓是一个正方体,从正面和左面看是一个正方形中间有一个圆形的孔。从而知这两个面应该都有一个圆柱形的孔。
解:由此可以推测该物体大致形状如图所示。
7.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原来三角形面积的( )
A.倍 B.倍 C.倍 D.倍
分析:直观图也是三角形,并且有一条公共边,但是这条公共边上的高发生变化。直观图中公共边上的高是原三角形中公共边上高的,则直观图的面积是原来三角形面积的倍。
答案:A
空间几何体的直观图
No.039 班级 姓名 学号 成绩
A 组
1.根据斜二测画法的规则画直观图时,把、、轴画成对应的、、,做与的度数分别为( )
A. B. C. D.或
2.关于“斜二测”直观图的画法,如下说法不正确的是( )
A.原图形中平行于轴的线段,其对应线段平行于轴,长度不变
B.原图形中平行于轴的线段,其对应线段平行于轴,长度变为原来的
C.画与直角坐标系对应的时,必须是
D.在画直观图时,由于选轴的不同,所得的直观图可能不同
3.两条相交直线的平行投影是( )
A.两条相交直线 B.一条直线
C.一条折线 D.两条相交直线或一条直线
4.下列叙述中正确的个数是( )
①相等的角,在直观图中仍相等;
②长度相等的线段,在直观图中长度仍相等;
③若两条线平行,在直观图中对应的线段仍平行;
④若两条线段垂直,则在直观图中对应的线段也互相垂直。
A.0 B.1 C.2 D.3
B 组
5.水平放置的有一边在水平线上,它的直观图是正,则( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
6.一个水平放置的平面图形的斜二测直观图是一个底角为、腰和上底均为1的等腰梯形,则这个平面图形的面积是( )
A. B. C. D.
7.一个长方体去掉一角的直观图和图中所示。关于它的三视图,下列画法正确的是( )
8.如图所示的水平放置的三角形的直观图,是中边的中点,那么、、三条线段对应原图形中线段AB、AD、AC中( )
A.最长的是AB,最短的是AC
B.最长的是AC,最短的是AB
C.最长的是AB,最短的是AD D.最长的是AD,最短的是AC
9.平面直角坐标系中点在直观图中对应点,则的找法是 。
10.若线段AB平行于投影面,O是AB上一点,且,则O的平行投影分AB的平行投影的长度之比为 。
C 组
11.如图是一个几何体的三视图,用斜二测画法画出它的直观图。
12.画水平放置的正五边形的直观图。
1.3 空间几何体的表面积与体积
一、三维目标
1.体会球的体积和表面积公式的推导过程,了解无限分割取极限的思想方法。
2.记住球的体积公式和表面积公式,会运用公式进行计算。
二、导学提纲自学
1.棱柱的侧面展开图是由 ,棱锥的侧面展开图是由 ,梭台的侧面展开图是由 ,圆柱的侧面展开图是 ,圆锥的侧面展开图是 ,圆台的侧面展开图是 。
2.几何体的表面积是指 ,棱柱、棱锥、棱台的表面积问题就是求 、 ,圆柱、圆锥、圆台的表面积问题就是求 、
、 、 。
3.几何体的体积是指 ,一个几何体的体积等于 。
4.柱体、锥体、台体的体积有何关系?
三、小试牛刀
1.一个长方体的三个面的面积分别为,则这个长方体的体积为( )
A.6 B. C.3 D.
2.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是,则母线长为( )
A.2 B. C. D.8
3.长、宽、高分别为的长方体的表面积S= 。
4.圆台的上、下底面半径分别为2,4,母线长为,则这个圆台的体积V= 。
三、典例剖析
1.已知圆柱和圆锥的高、底面半径均分别相等。若圆柱的底面半径为,圆柱侧面积为S,求圆锥的侧面积。
解:设圆锥的母线长为,因为圆柱的侧面积为S,圆柱的底面半径为,即,根据圆柱的侧面积公式可得:圆柱的母线(高)长为,由题意得圆锥的高为,又圆柱的底面半径为,根据勾股定理,圆锥的母线长,根据圆锥的侧面积公式得
2.两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( )
A.1:2:3 B.1:7:19 C.3:4:5 D.1:9:27
分析:因为圆锥的高被分成的三部分相等,所以两个截面的半径与原圆锥底面半径之比为1:2:3,于是自上而下三个圆锥的体积之比为· ,所以圆锥被分成的三部分的体积之比为
答案:B
3.三棱锥的中截面是,则三棱锥与三棱锥的体积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
分析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1:4,将三棱锥转化为三棱锥,这样三棱锥与三棱锥的高相等,底面积之比为1:4,于是其体积之比为1:4。
答案:B
4.如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )
A.1 B. C. D.
活动:让学生将三视图还原为实物图,讨论和交流该几何体的结构特征。
分析:根据三视图,可知该几何体是三棱锥,图中所示为该三棱锥的直观图,并且侧棱则该三棱锥的高是PA,底面三角形是直角三角形,所以这个几何体的体积为
答案:D
点评:本题订考查几何体的三视图和体积,给出几何体的三视图,求该几何体的体积或面积时,首先根据三视图确定该几何体的结构特征,再利用公式求得,此类题目成为新课标高考的热点,应引起重视。
5.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
A. B. C. D.
分析:该正三棱柱的直观图如图所示,且底面等边三角形的高为,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为
答案:C
6.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )
A. B. C. D.
分析:由三视图知该几何体是圆锥,且轴截面是等边三角形,其边长等于底面直径2,则圆锥的高是轴截面等边三角形的高为,所以这个几何体的体积为
答案:A
7.已知某几何体的俯视图如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形。
(1)求该几何体的体积V;
(2)求该几何体的侧面积S。
解:由三视图可知该几何体是一个底面边长分别为6、8的矩形,高为4的四棱锥。设底面矩形为ABCD。如图所示,,高
(1)
(2)设四棱锥侧面VAD、VBC是全等的等腰三角形,侧面VAB、VCD也是全等的等腰三角形,
在中,BC边上的高为,
在中,AB边上的高为
所以此几何体的侧面积
点评:高考试题中对面积和体积的考查有三种方式,一是给出三视图,求其面积或体积;二是与的组合体有关的面积和体积的计算;三是在解答题中,作为最后一问。
8.如图所示,圆锥的底面半径为1,高为,则圆锥的表面积为( )
A. B. C. D.
分析:设圆锥的母线长为,则,所以圆锥的表面积为
答案:C
9.正三棱锥的底面边长为3,侧棱长为,则这个正三棱锥的体积是( )
A. B. C. D.
分析;可得正三棱锥的高,于是
答案:D
10.若圆柱的高扩大为原来的4倍,底面半径不变,则圆柱的体积扩大为原来的 倍;若圆柱的高不变,底面半径扩大为原来的4倍,则圆柱的体积扩大为原来的 倍。
分析:圆柱的体积公式为,底面半径不变,高扩大为原来的4倍,其体积也变为原来的4倍;当圆柱的高不变,底面半径扩大为原来的4倍时,其体积变为原来的倍。
答案:4 16
11.右图是一个正方体,H、G、F分别是棱AB、AD、的中点。现在沿所在平面锯掉正方体的一个角,问锯掉部分的体积是原正方体体积的几分之几?
分析:因为锯掉的正方体的一个角,所以HA与AG、AF都垂直,即HA垂直于立方体的上底面,实际上锯掉的这个角,是以三角形AGF为底面,H为顶点的一个三棱锥。
解:设正方体的棱长淡,则正方体的体积为
三棱锥的底面是,即为,G、F又分别为AD、AA1的中点,所以所以的面积为又因AH是三棱锥的高,H又是AB的中点,所以所以锯掉的部分的体积为
又因,所以锯掉的那块的体积是原正方体体积的
12.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是 。
分析:如图,设圆锥底面半径为母线长为由题意得解得所以圆锥的底面积为
答案:
13.如图,一个正三棱柱容顺路,底面边长为,高为,内装水若干,将容器放倒,把一个侧面作为底面,如图,这时水面恰好为中截面,则图中容器内水面的高度是 。
分析:图中容器内水面的高度为,水的体积为V,则又图23中水组成了一个直四棱柱,其底面积为,高度为,则
答案:
14.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B.
C. D.
分析:该几何体是四棱锥,并且长为20cm的一条侧棱垂直于底面,所以四棱锥的高为20cm,底面是边长为20cm的正方形(如俯视图),所以底面积是,所以该几何体的体积是
答案:B
15.问题:有两个相同的直三棱柱,高为,底面三角形的三边长分别为用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则的取值范围是 。
探究:两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱,有三种情况:
四棱柱有一种,就是边长为的边重合在一起,表面积为,三棱柱有两种,边长为的边重合在一起,表面积为,边长为的边重合在一起,表面积为,两个相同的直三棱柱竖直放在一起,有一种情况,表面积为,
最小的是一个四棱柱,这说明
答案:
空间几何体的表面积与体积
No.040 班级 姓名 学号 成绩
A 组
1.正方体的全面积是96,则正方体的体积是( )
A. B. C.16 D.96
2.若圆台的上、下底面半径分别是1和3,它的侧面积是两底面面积和的2倍,则圆台的母线长是( )
A.2 B.2.5 C.5 D.10
3.若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
A.倍 B.3倍 C.2倍 D.5倍
4.如图,在四正体中,截面AEF经过四面体的内切球(与四个面都相切的球)的球心O,且分别截BC、DC于点E、F。如果截面将四面体分为体积相等的两部分,设四棱锥与三棱锥的表面积分为、,则必有( )
A. B. C. D.不能确定
5、如图,在正方体中,三棱锥的表面积与正方体的表面积的比为( )
A. B. C. D.
B 组
5.六棱柱的两底面是正六边形,侧面是全等的矩形,它的底面边长为4,高为12,则它的全面积是( )
A. B.
C. D.
6.若长方体的三个面的面积分别是则长方体的体积为( )
A. B. C.6 D.12
7.五棱台的上、下底面均是正五边形,边长分别为4cm和6cm,侧面是全等的等腰梯形,侧棱长是5cm,则它的侧面积是 。
8.正三棱锥的底面边长是,高是,则它的全面积为 。
9.圆台的两个底面半径是2cm、4cm,截得这个圆台的圆锥的高为6cm,则这个圆台的体积是 。
C 组
10.由8个面围成的几何体,每一个面都是正三角形,且有四个顶点A、B、C、D在同一个平面内,ABCD是边长为20cm的正方形,求此几何体的表面积和体积。
11.一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为 cm2。
12.圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,顶点均在上、下底面的圆周上是正三角形,如果三棱柱的体积为V,圆柱的底面直径与母线长相等,那么圆柱的体积为多少?
13:如图所示,在长方体中,用截面截下一个棱锥,求棱锥的体积与剩余部分的体积之比。
14:如图,已知三棱锥的底面是等边三角形,三条侧棱长都等于1且,M、N分别在棱AC和AD上,求BM+MN+NB的最小值。
21世纪教育网
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.2 空间几何体的三视图
一、三维目标
1.了解平行投影与中心投影的概念和简单性质。
2 理解三视图的含义,能画出简单几何体的三视图,掌握画法规则。
3.能根据三视图,运用空间想象能力,识别并说出它所表示的空间图形。
二、导学提纲
1.平行投影的投影线互相平行,而中心投影的投影线 。在平行投影中,投影线 时,叫做正投影,否则叫做 。21世纪教育网
2.空间几何体的三视图是指 、 、 。
3.三视图的排列规则是 放在正视图的下方,长度与正视图一样, 放在正视图一样,宽度与俯视图的宽度一样。
4.三视图的正视图、俯视图、侧视图分别是从 、 、 观察同一个几何体,画出的空间几何体的图形。
5.三视图对于认识空间几何体有何作用?你有何体会?
三小试牛刀
1.下列命题正确的是( )
A.一个点在一个平面内的投影仍是一个点
B.一条线段在一个平面内的投影仍是线段
C.一条直线在一个平面内的投影仍是一条直线
D.一个三角形在一个平面内的投影仍是三角形
2.一个圆柱的三视图中,一定没有的图形是( )
A.正方形 B.长方形 C.三角形 D.圆
3.一个正方形的平行投影的形状可能是 。
4.一个几何体的三视图如下图。
则这个几何体的名称是 。
四、典例剖析
1.如图甲所示,在正方体中,E、F分别是、的中点,G是正方形的中心,则四边形AGFE在该正方体的各个面上的投影可能是图乙中的 。
分析:在面ABCD和面上的投影是图乙(1);在面和面上的投影是图乙(2);在面和面上的投影是图乙(3)。
答案:(1)(2)(3)
点评:本题主要考查平行投影和空间想象能力。画出一个图形在一个平面上的投影的关键是确定该图形的关键点,如顶点等,画出这些关键点的投影,再依次连接即可得此图形在该平面上的投影。如果对平行投影理解不充分,做该类题目容易出现不知所措的情形,避免出现这种情况的方法是依据平行投影的含义,借助于空间相象来完成。
2.如图(1)所示,E、F分别为正方体面、面的中心,则四边形在该正方体的各个面上的投影可能是图(2)的 。
分析:四边形在正方体的面、面上的投影是C;在面上的投影是B;同理,在面、面、面上的投影也全是B。
答案:B C
3.右图是一几何体的三视图,想象该几何体的几何结构特征,画出该几何体的形状。
分析:由于俯视图有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接成的组合体,结合侧视图和正视图,可知该几何体是上面一个圆柱,下面是一个四棱柱拼接成的组合体。
答案:上面一个圆柱,下面是一个四棱柱拼接成的组合体,该几何体的形状如图所示。
4.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
分析:正方体的三视图都是正方形,所以①不符合题意,排除A、B、C。
答案:D
点评:虽然三视图的画法比较繁琐,但是三视图是考查空间想象能力的重要形式,因此是新课标高考的必考内容之一,足够的空间想象能力才能保证顺利解决三视图问题。
5.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥
C.四棱台 D.三棱台
分析:由所给三视图可以判定对应的几何体是四棱锥。
答案:B
6.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是( )
A.8 B.7 C.6 D.5
分析:由正视图和侧视图可知,该几何体有两层小正方体拼接成,由俯视图,可知最下层有5个小正方体,由侧视图可知上层仅有一个正方体,则共有6个小正方体。
答案:C
空间几何体的三视图
No.038 班级 姓名 学号 成绩
A 组
1.直线的平行投影可能是( )
A.点 B.线段 C.射线 D.曲线
2.如图所示,空心圆柱体的正视图是( )
3.如图,下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①② B.①③ C.①④ D.②④
4.三棱柱,如图所示,以的前面为正前方画出的三视图正确的是( )
B 组
5.如图所示是一个几何体,则其几何体俯视图是( )
6.下列物体的正视图和俯视图中有错误的一项是( )
7.下列各图,是正六棱柱的三视图,其中画法正确的是( )
8.如图,图(1)、(2)、(3)是图(4)所表示的几何体的三视图,其中图(1)是 ,图(2)是 ,图(3)是 。(说出视图名称)
C 组
9.根据图中的三视图想象物体原形,并分别画出物体的实物图。
10.如图,E、F分别是正方体的面和面的中心,则四边形在该正方体的面上的正投影(投射线垂直于投影面的投影)可能是图中 (把所有可能图形的序号都填上)。
1.2 空间几何体的直观图
一、三维目标
1.体会平面图形和空间图形的直观图的含义。
2.结合画直观图的实例,掌握直观图的斜二测画法及步骤。
3.会用斜二测画法画水平放置的平面图形的直观图。
4.会用斜二测画法画柱、锥、台、球及其简单组合体等空间图形的直观图。
二、导学提纲
1.表示空间图形的 ,叫做空间图形的直观图。
2.用斜二测画法画空间图形的直观图时,图形中平行于轴、轴或轴的线段,在直观图中分别画成 于轴、轴或轴的线段。平行于轴和轴的线段,在直观图中长度 ;平行于轴的线段,长度变为原来的 。
3.斜二测画法是一种特殊的 投影画法。
4.用斜二测画法画水平放置的平面图形时会改变两线段的关系吗?
三、小试牛刀
1.利用斜二测画法叙述正确的是( )
A.正三角形的直观图是正三角形 B.平行四边形的直观图是平行四边形
C.矩形的直观图是矩形 D.圆的直观图一定是圆
2.下列结论正确的是( )
A.相等的线段在直观图中仍然相等
B.若两条线段平行,则在直观图中对应的两条线段仍然平行
C.两个全等三角形的直观图一定也全等
D.两个图形的直观图是全等的三角形,则这两个图形是全等三角形
3.直角坐标系中一个平面图形上的一条线段AB的实际长度为4cm,若AB//轴,则画出直观图后对应的线段 ,若轴,则画出直观图后对应的线段= 。
4.水平放置的的斜二测直观图如图所示,已知,则AB边上的中线的实际长度为 。
四、典例剖析
1.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积是( )
A.16 B.64 C.16或64 D.都不对
分析:根据直观图的画法,平行于轴的线段长度不变,平行于轴的线段变为原来的一半,于是长为4的边如果平行于轴,则正方形边长为4,面积为16,边长为4的边如果平行于轴,则正方形边长为8,面积是64。
答案:C
2.利用斜二测画法画直观图时:
①三角形的直观图是三角形; ②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形; ④菱形的直观图是菱形。
以上结论中,正确的是 。
分析:斜二测画法保持平行性和相交性不变,即平行直线的直观图还是平行直线,相交直线的直观图还是相交直线,故①②正确;但是斜二测画法中平行于轴的线段,在直观图中长度为原来的一半,则正方形的直观图不是正方形,菱形的直观图不是菱形,所以③④错。
答案:①②
3.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是( )
A. B. C. D.都不对
分析:根据斜二测画法的规则,正三角形的边长是原三角形的底边长,原三角形的高是正三角形高的倍,而正三角形的高是,所以原三角形的高为,于是其面积为
答案:A
4.一个水平放置的平面图形的直观图是一个底角为,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
A. B. C. D.
分析:平面图形是上底长为1,下底长为,高为2的直角梯形。计算得面积为
答案:D
5.斜二测画法中,位于平面直角坐标系中的点的直观图中对应点是,则点的找法是 。
分析:在轴的正方向上取点,使,在轴上取点,使,过和分别作平行于轴和轴的直线的交点就是
答案:在中,过点和轴平行的直线与过和轴平行的直线的交点即是。
6.根据图中所示物体的三视图(阴影部分为空洞)描绘出物体的大致形状。
分析:根据该物体的三视图可以判断该物体的外轮廓是一个正方体,从正面和左面看是一个正方形中间有一个圆形的孔。从而知这两个面应该都有一个圆柱形的孔。
解:由此可以推测该物体大致形状如图所示。
7.若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原来三角形面积的( )
A.倍 B.倍 C.倍 D.倍
分析:直观图也是三角形,并且有一条公共边,但是这条公共边上的高发生变化。直观图中公共边上的高是原三角形中公共边上高的,则直观图的面积是原来三角形面积的倍。
答案:A
空间几何体的直观图
No.039 班级 姓名 学号 成绩
A 组
1.根据斜二测画法的规则画直观图时,把、、轴画成对应的、、,做与的度数分别为( )
A. B. C. D.或
2.关于“斜二测”直观图的画法,如下说法不正确的是( )
A.原图形中平行于轴的线段,其对应线段平行于轴,长度不变
B.原图形中平行于轴的线段,其对应线段平行于轴,长度变为原来的
C.画与直角坐标系对应的时,必须是
D.在画直观图时,由于选轴的不同,所得的直观图可能不同
3.两条相交直线的平行投影是( )
A.两条相交直线 B.一条直线
C.一条折线 D.两条相交直线或一条直线
4.下列叙述中正确的个数是( )
①相等的角,在直观图中仍相等;
②长度相等的线段,在直观图中长度仍相等;
③若两条线平行,在直观图中对应的线段仍平行;
④若两条线段垂直,则在直观图中对应的线段也互相垂直。
A.0 B.1 C.2 D.3
B 组
5.水平放置的有一边在水平线上,它的直观图是正,则( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
6.一个水平放置的平面图形的斜二测直观图是一个底角为、腰和上底均为1的等腰梯形,则这个平面图形的面积是( )
A. B. C. D.
7.一个长方体去掉一角的直观图和图中所示。关于它的三视图,下列画法正确的是( )
8.如图所示的水平放置的三角形的直观图,是中边的中点,那么、、三条线段对应原图形中线段AB、AD、AC中( )
A.最长的是AB,最短的是AC
B.最长的是AC,最短的是AB
C.最长的是AB,最短的是AD D.最长的是AD,最短的是AC
9.平面直角坐标系中点在直观图中对应点,则的找法是 。
10.若线段AB平行于投影面,O是AB上一点,且,则O的平行投影分AB的平行投影的长度之比为 。
C 组
11.如图是一个几何体的三视图,用斜二测画法画出它的直观图。
12.画水平放置的正五边形的直观图。
1.3 空间几何体的表面积与体积
一、三维目标
1.体会球的体积和表面积公式的推导过程,了解无限分割取极限的思想方法。
2.记住球的体积公式和表面积公式,会运用公式进行计算。
二、导学提纲自学
1.棱柱的侧面展开图是由 ,棱锥的侧面展开图是由 ,梭台的侧面展开图是由 ,圆柱的侧面展开图是 ,圆锥的侧面展开图是 ,圆台的侧面展开图是 。
2.几何体的表面积是指 ,棱柱、棱锥、棱台的表面积问题就是求 、 ,圆柱、圆锥、圆台的表面积问题就是求 、
、 、 。
3.几何体的体积是指 ,一个几何体的体积等于 。
4.柱体、锥体、台体的体积有何关系?
三、小试牛刀
1.一个长方体的三个面的面积分别为,则这个长方体的体积为( )
A.6 B. C.3 D.
2.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是,则母线长为( )
A.2 B. C. D.8
3.长、宽、高分别为的长方体的表面积S= 。
4.圆台的上、下底面半径分别为2,4,母线长为,则这个圆台的体积V= 。
三、典例剖析
1.已知圆柱和圆锥的高、底面半径均分别相等。若圆柱的底面半径为,圆柱侧面积为S,求圆锥的侧面积。
解:设圆锥的母线长为,因为圆柱的侧面积为S,圆柱的底面半径为,即,根据圆柱的侧面积公式可得:圆柱的母线(高)长为,由题意得圆锥的高为,又圆柱的底面半径为,根据勾股定理,圆锥的母线长,根据圆锥的侧面积公式得
2.两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( )
A.1:2:3 B.1:7:19 C.3:4:5 D.1:9:27
分析:因为圆锥的高被分成的三部分相等,所以两个截面的半径与原圆锥底面半径之比为1:2:3,于是自上而下三个圆锥的体积之比为· ,所以圆锥被分成的三部分的体积之比为
答案:B
3.三棱锥的中截面是,则三棱锥与三棱锥的体积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
分析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1:4,将三棱锥转化为三棱锥,这样三棱锥与三棱锥的高相等,底面积之比为1:4,于是其体积之比为1:4。
答案:B
4.如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )
A.1 B. C. D.
活动:让学生将三视图还原为实物图,讨论和交流该几何体的结构特征。
分析:根据三视图,可知该几何体是三棱锥,图中所示为该三棱锥的直观图,并且侧棱则该三棱锥的高是PA,底面三角形是直角三角形,所以这个几何体的体积为
答案:D
点评:本题订考查几何体的三视图和体积,给出几何体的三视图,求该几何体的体积或面积时,首先根据三视图确定该几何体的结构特征,再利用公式求得,此类题目成为新课标高考的热点,应引起重视。
5.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
A. B. C. D.
分析:该正三棱柱的直观图如图所示,且底面等边三角形的高为,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为
答案:C
6.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )
A. B. C. D.
分析:由三视图知该几何体是圆锥,且轴截面是等边三角形,其边长等于底面直径2,则圆锥的高是轴截面等边三角形的高为,所以这个几何体的体积为
答案:A
7.已知某几何体的俯视图如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形。
(1)求该几何体的体积V;
(2)求该几何体的侧面积S。
解:由三视图可知该几何体是一个底面边长分别为6、8的矩形,高为4的四棱锥。设底面矩形为ABCD。如图所示,,高
(1)
(2)设四棱锥侧面VAD、VBC是全等的等腰三角形,侧面VAB、VCD也是全等的等腰三角形,
在中,BC边上的高为,
在中,AB边上的高为
所以此几何体的侧面积
点评:高考试题中对面积和体积的考查有三种方式,一是给出三视图,求其面积或体积;二是与的组合体有关的面积和体积的计算;三是在解答题中,作为最后一问。
8.如图所示,圆锥的底面半径为1,高为,则圆锥的表面积为( )
A. B. C. D.
分析:设圆锥的母线长为,则,所以圆锥的表面积为
答案:C
9.正三棱锥的底面边长为3,侧棱长为,则这个正三棱锥的体积是( )
A. B. C. D.
分析;可得正三棱锥的高,于是
答案:D
10.若圆柱的高扩大为原来的4倍,底面半径不变,则圆柱的体积扩大为原来的 倍;若圆柱的高不变,底面半径扩大为原来的4倍,则圆柱的体积扩大为原来的 倍。
分析:圆柱的体积公式为,底面半径不变,高扩大为原来的4倍,其体积也变为原来的4倍;当圆柱的高不变,底面半径扩大为原来的4倍时,其体积变为原来的倍。
答案:4 16
11.右图是一个正方体,H、G、F分别是棱AB、AD、的中点。现在沿所在平面锯掉正方体的一个角,问锯掉部分的体积是原正方体体积的几分之几?
分析:因为锯掉的正方体的一个角,所以HA与AG、AF都垂直,即HA垂直于立方体的上底面,实际上锯掉的这个角,是以三角形AGF为底面,H为顶点的一个三棱锥。
解:设正方体的棱长淡,则正方体的体积为
三棱锥的底面是,即为,G、F又分别为AD、AA1的中点,所以所以的面积为又因AH是三棱锥的高,H又是AB的中点,所以所以锯掉的部分的体积为
又因,所以锯掉的那块的体积是原正方体体积的
12.已知一圆锥的侧面展开图为半圆,且面积为S,则圆锥的底面面积是 。
分析:如图,设圆锥底面半径为母线长为由题意得解得所以圆锥的底面积为
答案:
13.如图,一个正三棱柱容顺路,底面边长为,高为,内装水若干,将容器放倒,把一个侧面作为底面,如图,这时水面恰好为中截面,则图中容器内水面的高度是 。
分析:图中容器内水面的高度为,水的体积为V,则又图23中水组成了一个直四棱柱,其底面积为,高度为,则
答案:
14.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B.
C. D.
分析:该几何体是四棱锥,并且长为20cm的一条侧棱垂直于底面,所以四棱锥的高为20cm,底面是边长为20cm的正方形(如俯视图),所以底面积是,所以该几何体的体积是
答案:B
15.问题:有两个相同的直三棱柱,高为,底面三角形的三边长分别为用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则的取值范围是 。
探究:两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱,有三种情况:
四棱柱有一种,就是边长为的边重合在一起,表面积为,三棱柱有两种,边长为的边重合在一起,表面积为,边长为的边重合在一起,表面积为,两个相同的直三棱柱竖直放在一起,有一种情况,表面积为,
最小的是一个四棱柱,这说明
答案:
空间几何体的表面积与体积
No.040 班级 姓名 学号 成绩
A 组
1.正方体的全面积是96,则正方体的体积是( )
A. B. C.16 D.96
2.若圆台的上、下底面半径分别是1和3,它的侧面积是两底面面积和的2倍,则圆台的母线长是( )
A.2 B.2.5 C.5 D.10
3.若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
A.倍 B.3倍 C.2倍 D.5倍
4.如图,在四正体中,截面AEF经过四面体的内切球(与四个面都相切的球)的球心O,且分别截BC、DC于点E、F。如果截面将四面体分为体积相等的两部分,设四棱锥与三棱锥的表面积分为、,则必有( )
A. B. C. D.不能确定
5、如图,在正方体中,三棱锥的表面积与正方体的表面积的比为( )
A. B. C. D.
B 组
5.六棱柱的两底面是正六边形,侧面是全等的矩形,它的底面边长为4,高为12,则它的全面积是( )
A. B.
C. D.
6.若长方体的三个面的面积分别是则长方体的体积为( )
A. B. C.6 D.12
7.五棱台的上、下底面均是正五边形,边长分别为4cm和6cm,侧面是全等的等腰梯形,侧棱长是5cm,则它的侧面积是 。
8.正三棱锥的底面边长是,高是,则它的全面积为 。
9.圆台的两个底面半径是2cm、4cm,截得这个圆台的圆锥的高为6cm,则这个圆台的体积是 。
C 组
10.由8个面围成的几何体,每一个面都是正三角形,且有四个顶点A、B、C、D在同一个平面内,ABCD是边长为20cm的正方形,求此几何体的表面积和体积。
11.一个正四棱柱的各个顶点在一个直径为2cm的球面上。如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为 cm2。
12.圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,顶点均在上、下底面的圆周上是正三角形,如果三棱柱的体积为V,圆柱的底面直径与母线长相等,那么圆柱的体积为多少?
13:如图所示,在长方体中,用截面截下一个棱锥,求棱锥的体积与剩余部分的体积之比。
14:如图,已知三棱锥的底面是等边三角形,三条侧棱长都等于1且,M、N分别在棱AC和AD上,求BM+MN+NB的最小值。
21世纪教育网
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
