2015秋冀教版数学九上第二十五章第5节相似三角形的性质课件
文档属性
| 名称 | 2015秋冀教版数学九上第二十五章第5节相似三角形的性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 360.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-06 14:06:32 | ||
图片预览





文档简介
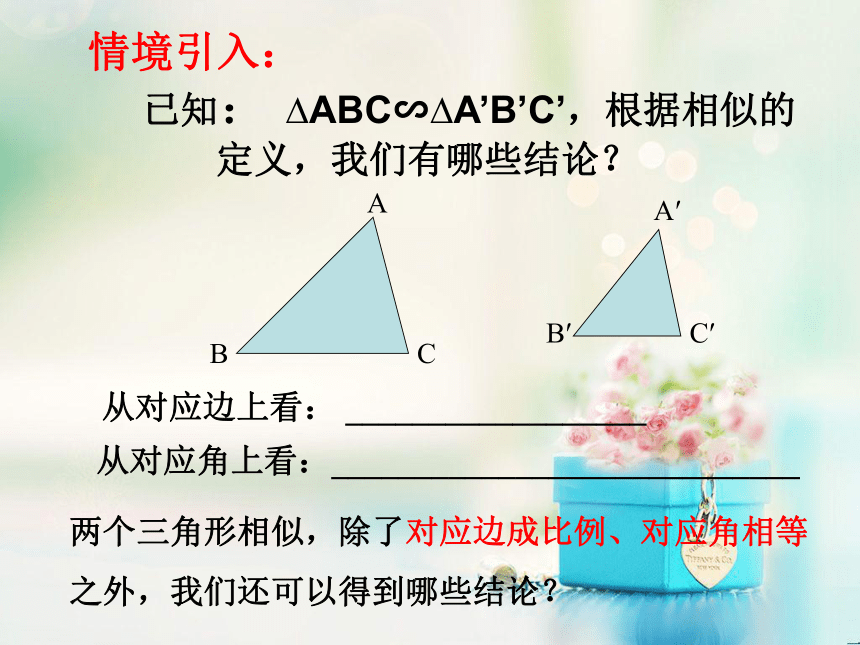
课件13张PPT。相似三角形的性质 已知: ?ABC∽?A’B’C’,根据相似的定义,我们有哪些结论?情境引入:从对应边上看: __________________从对应角上看:____________________________两个三角形相似,除了对应边成比例、对应角相等之外,我们还可以得到哪些结论? 例如:△ABC和△A′B′C′相似三角形,
相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、 A′D′之间有什么关系? 由此可以得出结论: 相似三角形对应高的比等于相似比 变化一:如果把对应的高改为对应边上的中线?变化二:如果把对应的高改为对应角的角平分线?我们再用心来观察下面一组图形:图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似?为什么?(2)与(1)的相似比=________________, ?
(2)与(1)的周长比=________________; ?
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________, ?
(3)与(1)的周长比=________________. ?
(3)与(1)的面积比=________________. ?由此可以得出结论: 相似三角形的周长比等于_____________. ? 由可以得出结论: 相似三角形的面积比
等于___________.
?
我来试一试:1.相似三角形对应边的比为3∶5 ,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。变化:相似三角形对应边的比为9∶8?相似三角形对应边的比为0.5?2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____, 周长比为___ . 3.两个相似三角形对应中线的比为1:4,则对应高的比为______ ,面积比为______。例题:求:BC、AC、 、 例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为 , 求四边形BCDE的面积。AEBDC展示风采:1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.1:21:43.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
4、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。 6、如图在 ABCD中,E是BC的中点,F是BE的中点,AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。 1:4今天我们学习相似三角形哪些性质?1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。课堂小结
相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、 A′D′之间有什么关系? 由此可以得出结论: 相似三角形对应高的比等于相似比 变化一:如果把对应的高改为对应边上的中线?变化二:如果把对应的高改为对应角的角平分线?我们再用心来观察下面一组图形:图中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似?为什么?(2)与(1)的相似比=________________, ?
(2)与(1)的周长比=________________; ?
(2)与(1)的面积比=________________;
(3)与(1)的相似比=________________, ?
(3)与(1)的周长比=________________. ?
(3)与(1)的面积比=________________. ?由此可以得出结论: 相似三角形的周长比等于_____________. ? 由可以得出结论: 相似三角形的面积比
等于___________.
?
我来试一试:1.相似三角形对应边的比为3∶5 ,那么相似比为___________,对应角的角平分线的比为______,周长的比为_____,面积的比为_____。变化:相似三角形对应边的比为9∶8?相似三角形对应边的比为0.5?2.两个相似三角形对应高的比为2:5,则对应角平分线的比为____, 周长比为___ . 3.两个相似三角形对应中线的比为1:4,则对应高的比为______ ,面积比为______。例题:求:BC、AC、 、 例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为 , 求四边形BCDE的面积。AEBDC展示风采:1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.1:21:43.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
4、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。 6、如图在 ABCD中,E是BC的中点,F是BE的中点,AE与DF交于点H,过点H作MN⊥AD,垂足为M,
交BC于N,则NH:MH=______。 1:4今天我们学习相似三角形哪些性质?1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。课堂小结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
