第八单元 立体几何全章复习讲义(无答案)2023-2024学年高一数学(人教A版2019必修第二册)
文档属性
| 名称 | 第八单元 立体几何全章复习讲义(无答案)2023-2024学年高一数学(人教A版2019必修第二册) |  | |
| 格式 | docx | ||
| 文件大小 | 798.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 11:49:59 | ||
图片预览




文档简介
第八章 立体几何初步 立体几何初步全章复习四
知识点一 直线和平面平行的判定
(1)定义:直线和平面没有公共点,则称直线平行于平面;
(2)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。 符号:
注:1、利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
2、证线线平行的方法常用三角形中位线定理、平行四边形的性质、平行线分线段成比例定理、平行公理等.
典例1、能保证直线a与平面α平行的条件是( )
A.b α,a∥b B.b α,c∥α,a∥b,a∥c
C.b α,A、B∈a,C、D∈b,且AC=BD D.a α,b α,a∥b
知识拓展 :
1、平行问题的实质
(1)平行问题是以无公共点为主要特征的,直线和平面平行即直线与平面没有任何公共点,紧紧抓住这一点,平行的问题就可以顺利解决.
(2)正确理解直线与平面平行的判定定理和掌握直线和平面的位置关系是解决此类题目的关键,可以采用直接法,也可以使用排除法.
典例2、下列说法:①若直线a在平面α外,则a∥α;②若直线a∥b,直线b α,则a∥α;③若直线a∥b,b α,那么直线a就平行于平面α内的无数条直线. 其中说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
2、证明线面平行的方法、步骤
(1)利用判定定理判断或证明直线与平面平行的关键是在已知平面α内找一条直线b和已知直线a平行.即要证直线a与平面α平行,先证直线a与直线b平行.即由立体向平面转化.
(2)证明线面平行的一般步骤:①在平面内找一条直线;②证明线线平行;③由判定定理得出结论.
(3)在与中点有关的平行问题中,常考虑中位线定理.
典例3、如图,在底面为平行四边形的四棱锥P-ABCD 中,E是PC的中点.求证:PA∥平面BDE.
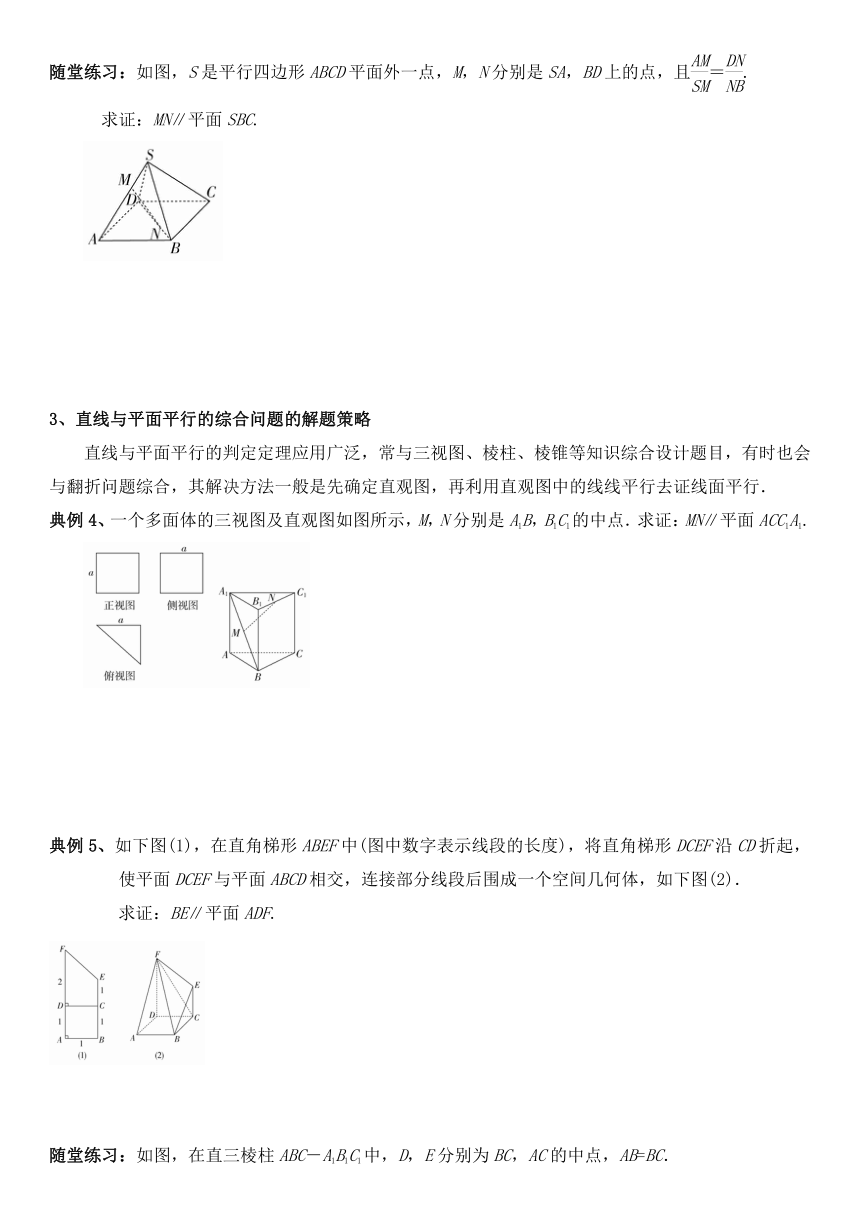
随堂练习:如图,S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且=.
求证:MN∥平面SBC.
3、直线与平面平行的综合问题的解题策略
直线与平面平行的判定定理应用广泛,常与三视图、棱柱、棱锥等知识综合设计题目,有时也会与翻折问题综合,其解决方法一般是先确定直观图,再利用直观图中的线线平行去证线面平行.
典例4、一个多面体的三视图及直观图如图所示,M,N分别是A1B,B1C1的中点.求证:MN∥平面ACC1A1.
典例5、如下图(1),在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF与平面ABCD相交,连接部分线段后围成一个空间几何体,如下图(2).
求证:BE∥平面ADF.
随堂练习:如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.
求证:A1B1平面DEC1.
知识点二 直线和平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行,则线线平行. 符号:
知识拓展:利用线面平行的性质定理解题的步骤
典例6、如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
典例7、如图所示,在四棱锥P-ABCD 中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.
随堂练习:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接FN,求证:FN∥CM.
知识点三 平面与平面平行的判定
(1)定义:两个平面没有公共点,称这两个平面平行;
(2)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
简记为:线面平行,则面面平行. 符号:
典例8、如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC//AB,
求证:平面PAB//平面EFG.
知识拓展:1、应用平面与平面平行判定定理注意事项
(1)平面与平面平行判定定理把判定面面平行转化为判定线面平行,同时应注意是两条相交直线都平行于另一平面.
(2)解决此类问题,若认为命题正确,必须用相关定理严格证明;而要否定它,只需要举出一个反例,此时借用常见几何模型是非常有效的方法.
典例9、平面与平面平行判定定理的理解
下列命题中正确的是( )
①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;
③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线分别平行于另一个平面,则这两个平面平行.
A.①③ B.②④ C.②③④ D.③④
随堂练习:设直线l,m,平面α,β,下列条件能得出α∥β的有( )
①l α,m α,且l∥β,m∥β; ②l α,m α,且l∥m,l∥β,m∥β;
③l∥α,m∥β,且l∥m; ④l∩m=P,l α,m α,且l∥β,m∥β.
A.1个 B.2个 C.3个 D.0个
2、线线平行、线面平行与面面平行的转化
(1)要证面面平行需证线面平行,要证线面平行需证线线平行,因此“面面平行”问题最终转化为“线线平行”问题.此即为面面平行判定定理的推论产生的依据.
(2)在转化为线面平行证面面平行时,首先观察面内已有的直线是否平行,若不平行,再利用条件有针对性地构造平面找出平行直线.
例10、已知在正方体ABCD-A1B1C1D1中,E,F分别是AA1,CC1的中点,求证:平面BDF∥平面B1D1E.
随堂练习:如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面; (2)平面EFA1∥平面BCHG.
3、三角形重心性质在解题中的应用
(1)要证明平面MNG∥平面ACD,主要是充分利用三角形重心的性质找出与平面平行的直线.
(2)求两个三角形的面积比,实质是求两个三角形对应边的平方比.
典例11、如图,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD,△BCD的重心.
(1)求证:平面MNG∥平面ACD; (2)求S△MNG∶S△DCA .
随堂练习:如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点.求证:平面EFG∥平面BDD1B1.
2、平面与平面平行的性质定理:如果两个平行的平面同时与第三个平面相交,那么它们的交线平行。
简记为:面面平行,则线线平行. 符号:
补充:平行于同一平面的两平面平行; 夹在两平行平面间的平行线段相等;
两平面平行,一平面上的任一条直线与另一个平面平行;
典例12四面体如图所示,过棱的中点作平行于,的平面,分别交四面体的棱于点.证明:四边形是平行四边形.
随堂练习:如图,在三棱锥中,,,分别是,,的中点.是上一点,连接,是与的交点,连接,求证:.
知识拓展:1、性质定理应用的注意事项
面面平行的性质定理是由面面平行得到线线平行.证明线线平行的关键是把要证明的直线看作是平面的交线,所以构造三个平面:即两个平行平面,一个经过两直线的平面,有时需要添加辅助面.
典例13、在三棱柱中,(1)若分别是的中点,求证:平面平面.(2)若点分别是上的点,且平面平面,试求的值.
2、空间平行关系的注意事项
直线与平面平行,平面与平面平行的判定定理、性质定理,揭示了线线平行、线面平行、面面平行之间的转化关系,具体转化过程如图所示.
典例14、如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.求证:在四棱锥P-ABCD中,AP平面EFG.
随堂练习:如图,已知点P是平行四边形ABCD所在平面外一点,M N分别是AB PC的中点
(1)求证:MN平面PAD;(2)在PB上确定一个点Q,使平面MNQ平面PAD.
3、线面、面面平行的判定与性质的综合应用
典例15、如图所示,矩形和矩形中,,点M,N分别位于上,且,矩形可沿任意翻折.(1)求证:当F,A,D不共线时,线段总平行于平面.
(2)“不管怎样翻折矩形,线段总和线段平行,”这个结论对吗?如果对,请证明;如果不对,请说明能否改变个别已知条件使上述结论成立.
典例16、如图,E,F,G,H分别是正方体ABCD A1B1C1D1的棱BC,CC1,C1D1,AA1的中点.
求证:(1)EG平面BB1D1D;(2)平面BDF平面B1D1H.
随堂练习:如图,在四棱锥中,四边形为平行四边形,,分别为,的中点,.求证:(1)平面;(2)平面平面.
课 后 练 习
一、单选题
1、在正六棱柱任意两个顶点的连线中与棱AB平行的条数为( )
A.2 B.3 C.4 D.5
2、如图,在三棱锥A-BCD中,E,F,G,H分别是边AC,CD,BD,AB的中点,且AD=BC,那么四边形EFGH是( ) A.平行四边形 B.矩形 C.菱形 D.正方形
(2) (5) (6)(8)
3、如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面平行的有( )个 A. B. C. D.
①. ②. ③. ④.
4、在空间四边形ABCD中,E,F分别为AB,AD上的点,且,H,G分别为BC,CD的中点,则( )
A.平面EFG,且四边形EFGH是平行四边形 B.平面BCD,且四边形EFGH是梯形
C.平面ABD,且四边形EFGH是平行四边形 D.平面ADC,且四边形EFGH是梯形
5、如图,已知四棱锥的底面是菱形,交于点O,E为的中点,F在上,,∥平面,则的值为( ) A.1 B. C.3 D.2
6、如图所示,正方体,E在上,F在上,且,过E作交BD于H,则平面EFH与平面的位置关系是( )
A.平行 B.相交 C.垂直 D.以上都有可能
7、正方体的棱长为2,E,F,G,H分别为,AD,,的中点,则过GH且与EF平行的平面截正方体所得的截面的面积为( ) A. B.2 C. D.4
8、在三棱台中,点在上,且,点是三角形内(含边界)的一个动点,且有平面平面,则动点的轨迹是( )
A.三角形边界的一部分 B.一个点 C.线段的一部分 D.圆的一部分
二、多选题
9、(多选题)下列命题中,错误的结论有( )
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
10、已知表示两条直线,表示三个不重合的平面,给出下列命题,正确的是( )
A.若,且,则 B.若相交,且都在外,,则
C.若,且,则 D.若,则
11、(多选题)如图是正方体的平面展开图,在这个正方体中,以下说法正确的是( )
A.BM∥平面ADE B.CN∥平面BAF C.平面BDM∥平面AFN D.平面BDE∥平面NCF
12、如图所示,在棱长为2的正方体中,E,F,G分别为所在棱的中点,P为平面内(包括边界)一动点,且平面EFG,则( )
A. B.平面EFG C.三棱锥的体积为 D.P点的轨迹长度为2
(12) (13)(14)(15)
三、填空题
13、如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
14、如图所示﹐在三棱柱中,截面与平面ABC交于直线a,则直线a与直线的位置关系为______.
15、如图,在正方体中,,,,分别是棱、、、的中点,是的中点,点在四边形及其内部运动,则满足________时,有平面.
16、在斜三棱柱中,点,分别为,上的点,若平面平面,则_______.
四、解答题
17、长方体中,分别为棱的中点.(1)求证:;(2)求证:.
18、如图,在三棱柱中,侧棱底面ABC,,D为AC的中点,,.
(1)求证:平面;(2)求三棱柱的表面积
19、如图,在四棱锥中,四边形为等腰梯形,,,M为上一点,且.(1)求证:平面;(2)若为正三角形,,求异面直线与所成角的余弦值;(3)若点P到底面的距离为3,求三棱锥的体积.
20、如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
求证:(1)l∥BC;(2)MN∥平面PAD.
21、如图,已知四边形ABCD是空间四边形,E是AB的中点,F、G分别是BC、CD上的点,且.
(1)设平面EFG∩AD=H,AD=λAH,求λ的值 (2)试证明四边形EFGH是梯形.
22、图,在正方体中,是的中点,,,分别是,,的中点.求证:
(1)直线平面; (2)平面平面;(3)若正方体棱长为1,过,,三点作正方体的截面,画出截面与正方体的交线,并求出截面的面积.
23、如图,在正三棱柱中,为棱的中点.(1)若是面积为6的直角三角形,则此三棱柱的体积为多少?(2)在线段上确定一点,使得平面,并说明理由.
24、如图所示,在四棱锥中,平面,,是的中点.
(1)求证:;(2)求证:平面;
(3)若是线段上一动点,则线段上是否存在点,使平面?说明理由.
知识点一 直线和平面平行的判定
(1)定义:直线和平面没有公共点,则称直线平行于平面;
(2)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。 符号:
注:1、利用直线与平面平行的判定定理证明线面平行,关键是寻找平面内与已知直线平行的直线.
2、证线线平行的方法常用三角形中位线定理、平行四边形的性质、平行线分线段成比例定理、平行公理等.
典例1、能保证直线a与平面α平行的条件是( )
A.b α,a∥b B.b α,c∥α,a∥b,a∥c
C.b α,A、B∈a,C、D∈b,且AC=BD D.a α,b α,a∥b
知识拓展 :
1、平行问题的实质
(1)平行问题是以无公共点为主要特征的,直线和平面平行即直线与平面没有任何公共点,紧紧抓住这一点,平行的问题就可以顺利解决.
(2)正确理解直线与平面平行的判定定理和掌握直线和平面的位置关系是解决此类题目的关键,可以采用直接法,也可以使用排除法.
典例2、下列说法:①若直线a在平面α外,则a∥α;②若直线a∥b,直线b α,则a∥α;③若直线a∥b,b α,那么直线a就平行于平面α内的无数条直线. 其中说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
2、证明线面平行的方法、步骤
(1)利用判定定理判断或证明直线与平面平行的关键是在已知平面α内找一条直线b和已知直线a平行.即要证直线a与平面α平行,先证直线a与直线b平行.即由立体向平面转化.
(2)证明线面平行的一般步骤:①在平面内找一条直线;②证明线线平行;③由判定定理得出结论.
(3)在与中点有关的平行问题中,常考虑中位线定理.
典例3、如图,在底面为平行四边形的四棱锥P-ABCD 中,E是PC的中点.求证:PA∥平面BDE.
随堂练习:如图,S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且=.
求证:MN∥平面SBC.
3、直线与平面平行的综合问题的解题策略
直线与平面平行的判定定理应用广泛,常与三视图、棱柱、棱锥等知识综合设计题目,有时也会与翻折问题综合,其解决方法一般是先确定直观图,再利用直观图中的线线平行去证线面平行.
典例4、一个多面体的三视图及直观图如图所示,M,N分别是A1B,B1C1的中点.求证:MN∥平面ACC1A1.
典例5、如下图(1),在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF与平面ABCD相交,连接部分线段后围成一个空间几何体,如下图(2).
求证:BE∥平面ADF.
随堂练习:如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.
求证:A1B1平面DEC1.
知识点二 直线和平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行,则线线平行. 符号:
知识拓展:利用线面平行的性质定理解题的步骤
典例6、如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.
典例7、如图所示,在四棱锥P-ABCD 中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH.
随堂练习:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接FN,求证:FN∥CM.
知识点三 平面与平面平行的判定
(1)定义:两个平面没有公共点,称这两个平面平行;
(2)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
简记为:线面平行,则面面平行. 符号:
典例8、如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC//AB,
求证:平面PAB//平面EFG.
知识拓展:1、应用平面与平面平行判定定理注意事项
(1)平面与平面平行判定定理把判定面面平行转化为判定线面平行,同时应注意是两条相交直线都平行于另一平面.
(2)解决此类问题,若认为命题正确,必须用相关定理严格证明;而要否定它,只需要举出一个反例,此时借用常见几何模型是非常有效的方法.
典例9、平面与平面平行判定定理的理解
下列命题中正确的是( )
①若一个平面内有两条直线都与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线都与另一个平面平行,则这两个平面平行;
③若一个平面内任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线分别平行于另一个平面,则这两个平面平行.
A.①③ B.②④ C.②③④ D.③④
随堂练习:设直线l,m,平面α,β,下列条件能得出α∥β的有( )
①l α,m α,且l∥β,m∥β; ②l α,m α,且l∥m,l∥β,m∥β;
③l∥α,m∥β,且l∥m; ④l∩m=P,l α,m α,且l∥β,m∥β.
A.1个 B.2个 C.3个 D.0个
2、线线平行、线面平行与面面平行的转化
(1)要证面面平行需证线面平行,要证线面平行需证线线平行,因此“面面平行”问题最终转化为“线线平行”问题.此即为面面平行判定定理的推论产生的依据.
(2)在转化为线面平行证面面平行时,首先观察面内已有的直线是否平行,若不平行,再利用条件有针对性地构造平面找出平行直线.
例10、已知在正方体ABCD-A1B1C1D1中,E,F分别是AA1,CC1的中点,求证:平面BDF∥平面B1D1E.
随堂练习:如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面; (2)平面EFA1∥平面BCHG.
3、三角形重心性质在解题中的应用
(1)要证明平面MNG∥平面ACD,主要是充分利用三角形重心的性质找出与平面平行的直线.
(2)求两个三角形的面积比,实质是求两个三角形对应边的平方比.
典例11、如图,B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD,△BCD的重心.
(1)求证:平面MNG∥平面ACD; (2)求S△MNG∶S△DCA .
随堂练习:如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点.求证:平面EFG∥平面BDD1B1.
2、平面与平面平行的性质定理:如果两个平行的平面同时与第三个平面相交,那么它们的交线平行。
简记为:面面平行,则线线平行. 符号:
补充:平行于同一平面的两平面平行; 夹在两平行平面间的平行线段相等;
两平面平行,一平面上的任一条直线与另一个平面平行;
典例12四面体如图所示,过棱的中点作平行于,的平面,分别交四面体的棱于点.证明:四边形是平行四边形.
随堂练习:如图,在三棱锥中,,,分别是,,的中点.是上一点,连接,是与的交点,连接,求证:.
知识拓展:1、性质定理应用的注意事项
面面平行的性质定理是由面面平行得到线线平行.证明线线平行的关键是把要证明的直线看作是平面的交线,所以构造三个平面:即两个平行平面,一个经过两直线的平面,有时需要添加辅助面.
典例13、在三棱柱中,(1)若分别是的中点,求证:平面平面.(2)若点分别是上的点,且平面平面,试求的值.
2、空间平行关系的注意事项
直线与平面平行,平面与平面平行的判定定理、性质定理,揭示了线线平行、线面平行、面面平行之间的转化关系,具体转化过程如图所示.
典例14、如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.求证:在四棱锥P-ABCD中,AP平面EFG.
随堂练习:如图,已知点P是平行四边形ABCD所在平面外一点,M N分别是AB PC的中点
(1)求证:MN平面PAD;(2)在PB上确定一个点Q,使平面MNQ平面PAD.
3、线面、面面平行的判定与性质的综合应用
典例15、如图所示,矩形和矩形中,,点M,N分别位于上,且,矩形可沿任意翻折.(1)求证:当F,A,D不共线时,线段总平行于平面.
(2)“不管怎样翻折矩形,线段总和线段平行,”这个结论对吗?如果对,请证明;如果不对,请说明能否改变个别已知条件使上述结论成立.
典例16、如图,E,F,G,H分别是正方体ABCD A1B1C1D1的棱BC,CC1,C1D1,AA1的中点.
求证:(1)EG平面BB1D1D;(2)平面BDF平面B1D1H.
随堂练习:如图,在四棱锥中,四边形为平行四边形,,分别为,的中点,.求证:(1)平面;(2)平面平面.
课 后 练 习
一、单选题
1、在正六棱柱任意两个顶点的连线中与棱AB平行的条数为( )
A.2 B.3 C.4 D.5
2、如图,在三棱锥A-BCD中,E,F,G,H分别是边AC,CD,BD,AB的中点,且AD=BC,那么四边形EFGH是( ) A.平行四边形 B.矩形 C.菱形 D.正方形
(2) (5) (6)(8)
3、如图,在下列四个正方体中,为正方体的两个顶点,为所在棱的中点,则在这四个正方体中,直线与平面平行的有( )个 A. B. C. D.
①. ②. ③. ④.
4、在空间四边形ABCD中,E,F分别为AB,AD上的点,且,H,G分别为BC,CD的中点,则( )
A.平面EFG,且四边形EFGH是平行四边形 B.平面BCD,且四边形EFGH是梯形
C.平面ABD,且四边形EFGH是平行四边形 D.平面ADC,且四边形EFGH是梯形
5、如图,已知四棱锥的底面是菱形,交于点O,E为的中点,F在上,,∥平面,则的值为( ) A.1 B. C.3 D.2
6、如图所示,正方体,E在上,F在上,且,过E作交BD于H,则平面EFH与平面的位置关系是( )
A.平行 B.相交 C.垂直 D.以上都有可能
7、正方体的棱长为2,E,F,G,H分别为,AD,,的中点,则过GH且与EF平行的平面截正方体所得的截面的面积为( ) A. B.2 C. D.4
8、在三棱台中,点在上,且,点是三角形内(含边界)的一个动点,且有平面平面,则动点的轨迹是( )
A.三角形边界的一部分 B.一个点 C.线段的一部分 D.圆的一部分
二、多选题
9、(多选题)下列命题中,错误的结论有( )
A.如果一个角的两边与另一个角的两边分别平行,那么这两个角相等
B.如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等
C.如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补
D.如果两条直线同时平行于第三条直线,那么这两条直线互相平行
10、已知表示两条直线,表示三个不重合的平面,给出下列命题,正确的是( )
A.若,且,则 B.若相交,且都在外,,则
C.若,且,则 D.若,则
11、(多选题)如图是正方体的平面展开图,在这个正方体中,以下说法正确的是( )
A.BM∥平面ADE B.CN∥平面BAF C.平面BDM∥平面AFN D.平面BDE∥平面NCF
12、如图所示,在棱长为2的正方体中,E,F,G分别为所在棱的中点,P为平面内(包括边界)一动点,且平面EFG,则( )
A. B.平面EFG C.三棱锥的体积为 D.P点的轨迹长度为2
(12) (13)(14)(15)
三、填空题
13、如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
14、如图所示﹐在三棱柱中,截面与平面ABC交于直线a,则直线a与直线的位置关系为______.
15、如图,在正方体中,,,,分别是棱、、、的中点,是的中点,点在四边形及其内部运动,则满足________时,有平面.
16、在斜三棱柱中,点,分别为,上的点,若平面平面,则_______.
四、解答题
17、长方体中,分别为棱的中点.(1)求证:;(2)求证:.
18、如图,在三棱柱中,侧棱底面ABC,,D为AC的中点,,.
(1)求证:平面;(2)求三棱柱的表面积
19、如图,在四棱锥中,四边形为等腰梯形,,,M为上一点,且.(1)求证:平面;(2)若为正三角形,,求异面直线与所成角的余弦值;(3)若点P到底面的距离为3,求三棱锥的体积.
20、如图所示,已知P是 ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
求证:(1)l∥BC;(2)MN∥平面PAD.
21、如图,已知四边形ABCD是空间四边形,E是AB的中点,F、G分别是BC、CD上的点,且.
(1)设平面EFG∩AD=H,AD=λAH,求λ的值 (2)试证明四边形EFGH是梯形.
22、图,在正方体中,是的中点,,,分别是,,的中点.求证:
(1)直线平面; (2)平面平面;(3)若正方体棱长为1,过,,三点作正方体的截面,画出截面与正方体的交线,并求出截面的面积.
23、如图,在正三棱柱中,为棱的中点.(1)若是面积为6的直角三角形,则此三棱柱的体积为多少?(2)在线段上确定一点,使得平面,并说明理由.
24、如图所示,在四棱锥中,平面,,是的中点.
(1)求证:;(2)求证:平面;
(3)若是线段上一动点,则线段上是否存在点,使平面?说明理由.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
