第7章 平面直角坐标系单元同步检测试题 2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 第7章 平面直角坐标系单元同步检测试题 2023-2024学年人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 595.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 08:53:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第七章《平面直角坐标系》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在平面直角坐标系中,已知点到x轴的距离为2,则a的值为( )
A.2 B.-2 C.±2 D.不能确定
2.点P(1,-4)所在的象限是( )
A.第三象限 B.第二象限 C.第一象限 D.第四象限
3.根据下列表述,不能确定具体位置的是( )
A.某电影院1号厅的3排4座 B.慈溪市孙塘北路824号
C.某灯塔南偏西30°方向 D.东经108°,北纬53°
4.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),则“炮”位于点( )
A.(1,3) B.(﹣2,0) C.(﹣1,2) D.(﹣2,2)
5、已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A.(3,-2) B.(-3,2) C.(3,-4) D.(-3,4)
6、已知点A(1,0)B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标
为( )
A.(-4,0) B.(6,0) C.(-4,0)或(6,0) D.(0,12)或(0,-8)
7.已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1 B.3 C.﹣1 D.5
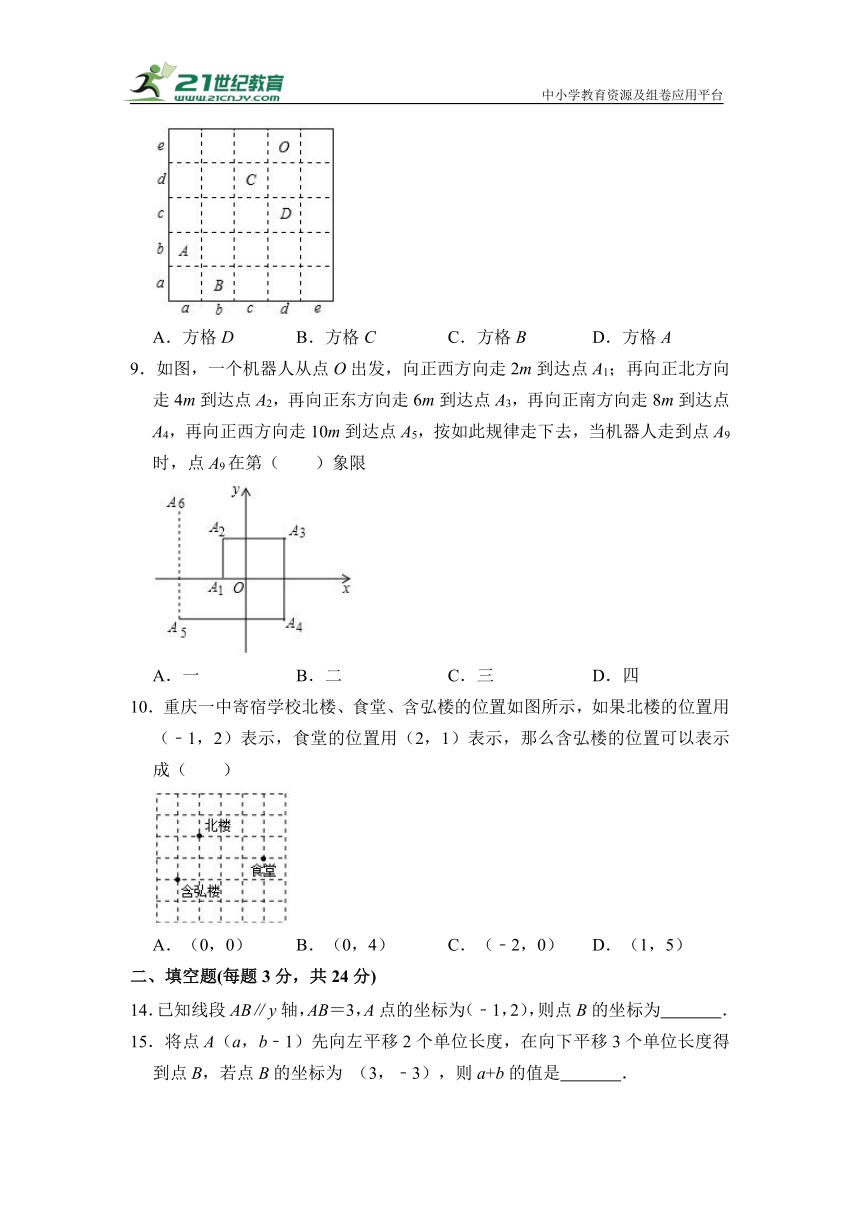
8.如图,网格图中的每一格的边长都相等,列和行都用字母标记,按照先列后行的顺序,方格O的位置可用(d,e)表示,则(c,d)可表示图中的( )
A.方格D B.方格C C.方格B D.方格A
9.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正西方向走10m到达点A5,按如此规律走下去,当机器人走到点A9时,点A9在第( )象限
A.一 B.二 C.三 D.四
10.重庆一中寄宿学校北楼、食堂、含弘楼的位置如图所示,如果北楼的位置用(﹣1,2)表示,食堂的位置用(2,1)表示,那么含弘楼的位置可以表示成( )
A.(0,0) B.(0,4) C.(﹣2,0) D.(1,5)
二、填空题(每题3分,共24分)
14.已知线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),则点B的坐标为 .
15.将点A(a,b﹣1)先向左平移2个单位长度,在向下平移3个单位长度得到点B,若点B的坐标为 (3,﹣3),则a+b的值是 .
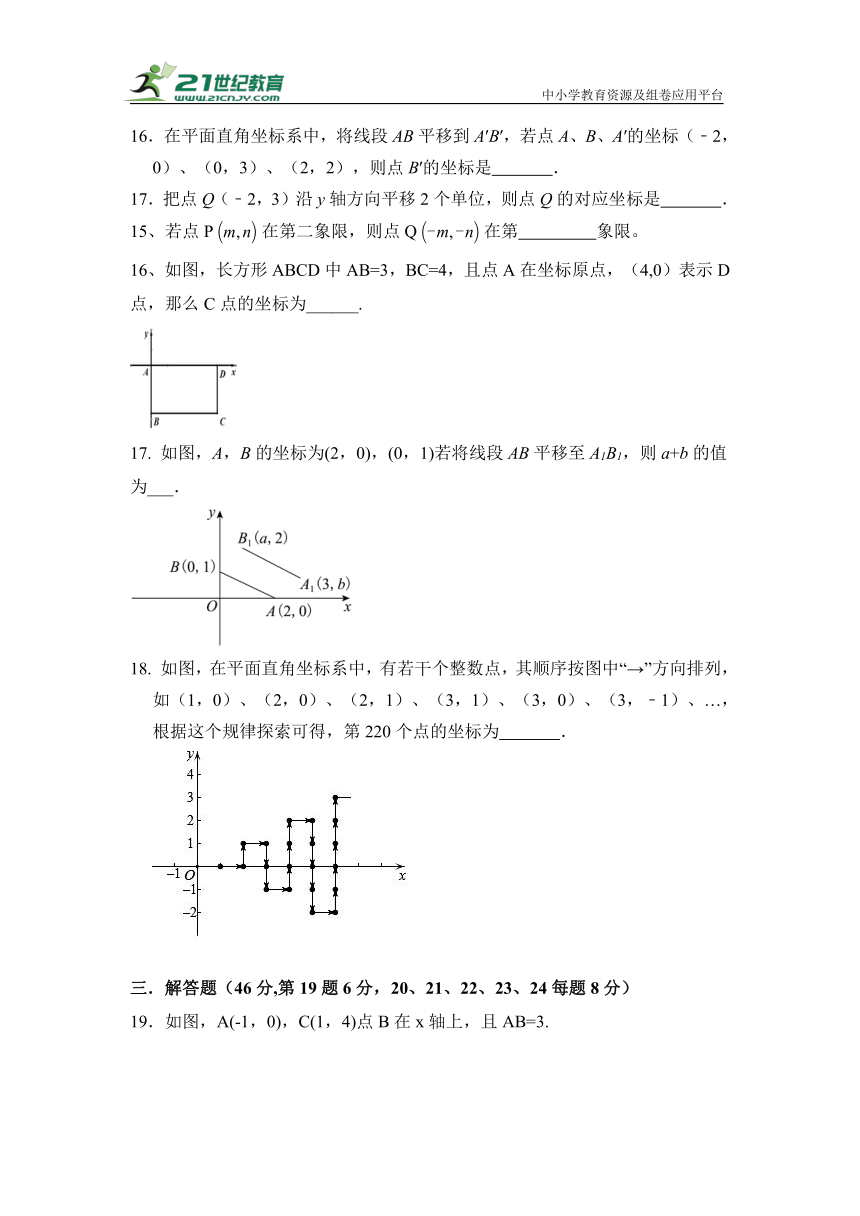
16.在平面直角坐标系中,将线段AB平移到A′B′,若点A、B、A′的坐标(﹣2,0)、(0,3)、(2,2),则点B′的坐标是 .
17.把点Q(﹣2,3)沿y轴方向平移2个单位,则点Q的对应坐标是 .
15、若点P在第二象限,则点Q在第 象限。
16、如图,长方形ABCD中AB=3,BC=4,且点A在坐标原点,(4,0)表示D点,那么C点的坐标为______.
17. 如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至A1B1,则a+b的值为___.
18. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0)、(2,0)、(2,1)、(3,1)、(3,0)、(3,﹣1)、…,根据这个规律探索可得,第220个点的坐标为 .
三.解答题(46分,第19题6分,20、21、22、23、24每题8分)
19.如图,A(-1,0),C(1,4)点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
20.如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(﹣4,1),B(﹣3,﹣4).
(1)将线段AB向上平移2个单位,再向右平移5个单位得到线段A'B',画出线段A'B'(点A',B'分别为
21.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
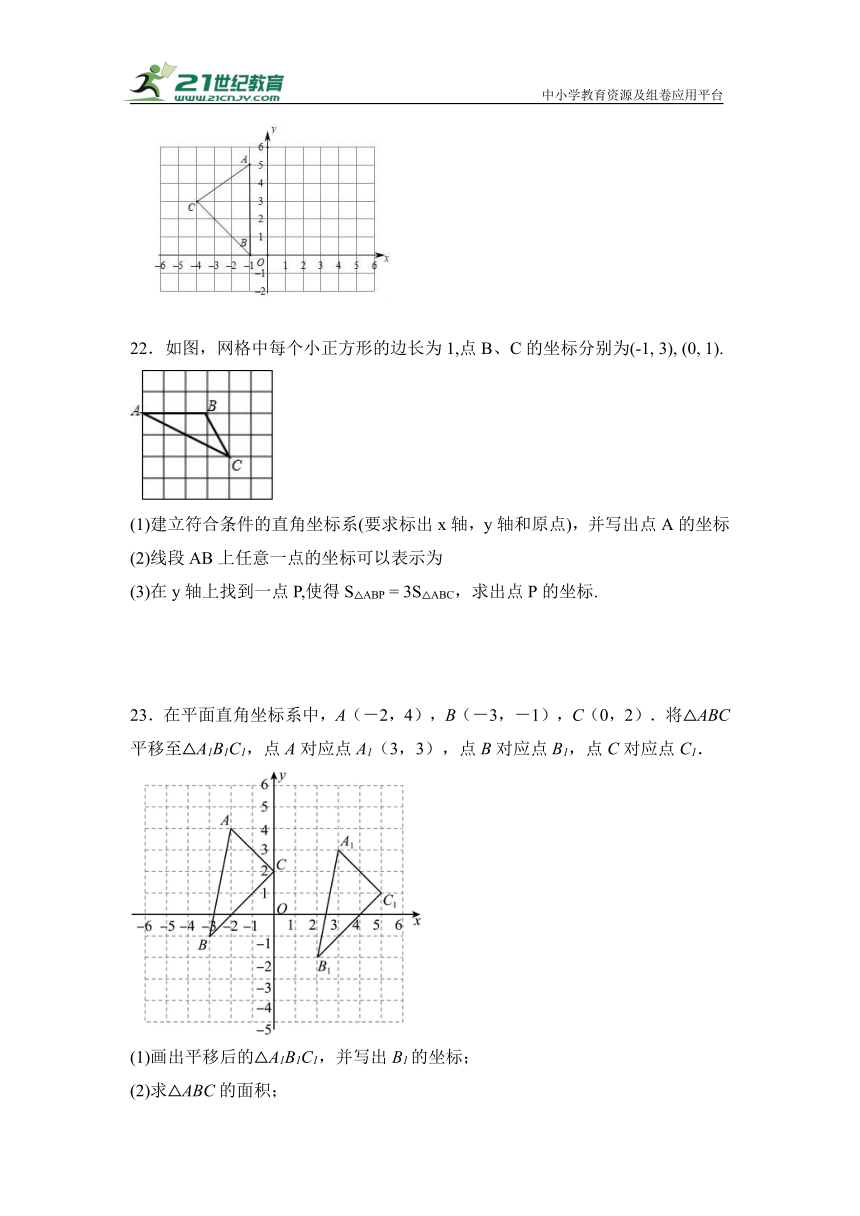
22.如图,网格中每个小正方形的边长为1,点B、C的坐标分别为(-1, 3), (0, 1).
(1)建立符合条件的直角坐标系(要求标出x轴,y轴和原点),并写出点A的坐标
(2)线段AB上任意一点的坐标可以表示为
(3)在y轴上找到一点P,使得S△ABP = 3S△ABC,求出点P的坐标.
23.在平面直角坐标系中,A(-2,4),B(-3,-1),C(0,2).将△ABC平移至△A1B1C1,点A对应点A1(3,3),点B对应点B1,点C对应点C1.
(1)画出平移后的△A1B1C1,并写出B1的坐标;
(2)求△ABC的面积;
(3)若存在点D(m,n)使得△BB1D和△BB1C面积相等,其中m,n均为绝对值不超过5的整数,则点D的坐标为_________.
24.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3),B(6,3),现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3)在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B D C B C C C
二、填空题:
11.【分析】根据线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),可以设出点B的坐标,列出方程,从而可以得到点B的坐标.
【解答】解:∵线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),
设点B的坐标为(﹣1,b),
∴|2﹣b|=3,
解得,b=﹣1或b=5,
∴点B的坐标为:(﹣1,﹣1)或(﹣1,5),
故答案为:(﹣1,﹣1)或(﹣1,5),
12.【分析】先将点A的横坐标减2、纵坐标减3表示出点B的坐标,再结合点B的坐标为 (3,﹣3)得出关于a、b的方程,解之可得.
【解答】解:点A(a,b﹣1)先向左平移2个单位长度,在向下平移3个单位长度得到点B的坐标可表示为(a﹣2,b﹣4),
∵点B的坐标为 (3,﹣3),
∴a﹣2=3,b﹣4=﹣3,
解得a=5,b=1,
则a+b=6,
故答案为:6.
13.【分析】根据点A的平移规律解决问题即可.
【解答】解:∵点A(﹣2,0)向右平移4个单位,向上平移2个单位得到A′(2,2),
∴点B(0,3)向右平移4个单位,向上平移2个单位得到B′(4,5),
故答案为(4,5).
14.【分析】根据上下平移纵坐标加或者减可得答案.
【解答】解:把点Q(﹣2,3)沿y轴方向平移2个单位,则点Q的对应点坐标是(﹣2,3+2)或(﹣2,3﹣2),即(﹣2,5)或(﹣2,1),
故答案为:(﹣2,5)或(﹣2,1).
15、四
16、(4,-3)
17. 18
18. (13,64) (15,-128)
三.解答题:
19.【答案】(1)解: ∵AB=3 ∴点B的坐标为(-4,0)或(2,0)
(2)解: S=3×4÷2=6.
【解析】【分析】根据AB的长度得出点B的坐标,根据三角形的面积计算公式求出三角形的面积.
20.【答案】(1)解:如图:线段 A'B' 就是所求作的线段.
(2)(m+5,n+2)
【解析】【解答】(2)解: 点P(m,n)为线段AB上任意一点,经过(1)的平移后,在线段A'B'上对应的点P'的坐标为(m+5,n+2).
故答案为:(m+5,n+2).
【分析】(1)利用方格纸的特点分别将点A、B向上平移2个单位,再向右平移5个单位得到对应点A'、B',再连接即可;
(2)根据点的坐标的平移规律“左减右加,上加下减”可直接得出点P'的坐标.
21.【分析】(1)根据三角形面积求法得出即可;
(2)根据已知将△ABC各顶点向下平移2个单位,向右平移5个单位得到各对应点,即可作图;进而得出点C′的坐标.
【解答】解:(1)△ABC的面积是:×3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
【点评】此题主要考查了平移变换以及三角形面积求法,正确平移图象的各顶点坐标是解题关键.
22.解:(1)如图所示,点A坐标为(-4,3);
(2)∵A(-4,3),B(-1,3)
∴线段AB上任意一点的坐标可表示为(x,3)(-4≤x≤-1).
(3)由图可得S△ABP=3S△ABC=,
P点坐标为(0,m),则
解得或9
所以P点坐标为(0,9)或(0,-3).
23.(1)如图,△A1B1C1即为所求,B1的坐标(2,﹣2);
(2)△ABC的面积=3×52×23×31×5=6;
(3)如图,点D的坐标为(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
故答案为:(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
24.(1)C(-2,0),D(4,0)
(2)t=2
(3)值不变,为6
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第七章《平面直角坐标系》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.在平面直角坐标系中,已知点到x轴的距离为2,则a的值为( )
A.2 B.-2 C.±2 D.不能确定
2.点P(1,-4)所在的象限是( )
A.第三象限 B.第二象限 C.第一象限 D.第四象限
3.根据下列表述,不能确定具体位置的是( )
A.某电影院1号厅的3排4座 B.慈溪市孙塘北路824号
C.某灯塔南偏西30°方向 D.东经108°,北纬53°
4.如图,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,﹣2),“象”位于点(3,﹣2),则“炮”位于点( )
A.(1,3) B.(﹣2,0) C.(﹣1,2) D.(﹣2,2)
5、已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A.(3,-2) B.(-3,2) C.(3,-4) D.(-3,4)
6、已知点A(1,0)B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标
为( )
A.(-4,0) B.(6,0) C.(-4,0)或(6,0) D.(0,12)或(0,-8)
7.已知点A(a﹣2,2a+7),点B的坐标为(1,5),直线AB∥y轴,则a的值是( )
A.1 B.3 C.﹣1 D.5
8.如图,网格图中的每一格的边长都相等,列和行都用字母标记,按照先列后行的顺序,方格O的位置可用(d,e)表示,则(c,d)可表示图中的( )
A.方格D B.方格C C.方格B D.方格A
9.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正西方向走10m到达点A5,按如此规律走下去,当机器人走到点A9时,点A9在第( )象限
A.一 B.二 C.三 D.四
10.重庆一中寄宿学校北楼、食堂、含弘楼的位置如图所示,如果北楼的位置用(﹣1,2)表示,食堂的位置用(2,1)表示,那么含弘楼的位置可以表示成( )
A.(0,0) B.(0,4) C.(﹣2,0) D.(1,5)
二、填空题(每题3分,共24分)
14.已知线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),则点B的坐标为 .
15.将点A(a,b﹣1)先向左平移2个单位长度,在向下平移3个单位长度得到点B,若点B的坐标为 (3,﹣3),则a+b的值是 .
16.在平面直角坐标系中,将线段AB平移到A′B′,若点A、B、A′的坐标(﹣2,0)、(0,3)、(2,2),则点B′的坐标是 .
17.把点Q(﹣2,3)沿y轴方向平移2个单位,则点Q的对应坐标是 .
15、若点P在第二象限,则点Q在第 象限。
16、如图,长方形ABCD中AB=3,BC=4,且点A在坐标原点,(4,0)表示D点,那么C点的坐标为______.
17. 如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至A1B1,则a+b的值为___.
18. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0)、(2,0)、(2,1)、(3,1)、(3,0)、(3,﹣1)、…,根据这个规律探索可得,第220个点的坐标为 .
三.解答题(46分,第19题6分,20、21、22、23、24每题8分)
19.如图,A(-1,0),C(1,4)点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
20.如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(﹣4,1),B(﹣3,﹣4).
(1)将线段AB向上平移2个单位,再向右平移5个单位得到线段A'B',画出线段A'B'(点A',B'分别为
21.如图,在直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位,再向右平移5个单位得到△A′B′C′,并写出C′的坐标.
22.如图,网格中每个小正方形的边长为1,点B、C的坐标分别为(-1, 3), (0, 1).
(1)建立符合条件的直角坐标系(要求标出x轴,y轴和原点),并写出点A的坐标
(2)线段AB上任意一点的坐标可以表示为
(3)在y轴上找到一点P,使得S△ABP = 3S△ABC,求出点P的坐标.
23.在平面直角坐标系中,A(-2,4),B(-3,-1),C(0,2).将△ABC平移至△A1B1C1,点A对应点A1(3,3),点B对应点B1,点C对应点C1.
(1)画出平移后的△A1B1C1,并写出B1的坐标;
(2)求△ABC的面积;
(3)若存在点D(m,n)使得△BB1D和△BB1C面积相等,其中m,n均为绝对值不超过5的整数,则点D的坐标为_________.
24.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,3),B(6,3),现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标;
(2)点M从O点出发,以每秒1个单位的速度向上平移运动.设运动时间为秒,问:是否存在这样的使得四边形OMDB的面积为12?若存在,请求出的值,若不存在,请说明理由.
(3)在(2)的条件下,点M从O点出发的同时,点N从D点出发,以每秒2个单位的速度向左平移运动,当点N到达点O时运动停止.设射线BN交轴于点E.设运动时间为秒,问:的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B D C B C C C
二、填空题:
11.【分析】根据线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),可以设出点B的坐标,列出方程,从而可以得到点B的坐标.
【解答】解:∵线段AB∥y轴,AB=3,A点的坐标为(﹣1,2),
设点B的坐标为(﹣1,b),
∴|2﹣b|=3,
解得,b=﹣1或b=5,
∴点B的坐标为:(﹣1,﹣1)或(﹣1,5),
故答案为:(﹣1,﹣1)或(﹣1,5),
12.【分析】先将点A的横坐标减2、纵坐标减3表示出点B的坐标,再结合点B的坐标为 (3,﹣3)得出关于a、b的方程,解之可得.
【解答】解:点A(a,b﹣1)先向左平移2个单位长度,在向下平移3个单位长度得到点B的坐标可表示为(a﹣2,b﹣4),
∵点B的坐标为 (3,﹣3),
∴a﹣2=3,b﹣4=﹣3,
解得a=5,b=1,
则a+b=6,
故答案为:6.
13.【分析】根据点A的平移规律解决问题即可.
【解答】解:∵点A(﹣2,0)向右平移4个单位,向上平移2个单位得到A′(2,2),
∴点B(0,3)向右平移4个单位,向上平移2个单位得到B′(4,5),
故答案为(4,5).
14.【分析】根据上下平移纵坐标加或者减可得答案.
【解答】解:把点Q(﹣2,3)沿y轴方向平移2个单位,则点Q的对应点坐标是(﹣2,3+2)或(﹣2,3﹣2),即(﹣2,5)或(﹣2,1),
故答案为:(﹣2,5)或(﹣2,1).
15、四
16、(4,-3)
17. 18
18. (13,64) (15,-128)
三.解答题:
19.【答案】(1)解: ∵AB=3 ∴点B的坐标为(-4,0)或(2,0)
(2)解: S=3×4÷2=6.
【解析】【分析】根据AB的长度得出点B的坐标,根据三角形的面积计算公式求出三角形的面积.
20.【答案】(1)解:如图:线段 A'B' 就是所求作的线段.
(2)(m+5,n+2)
【解析】【解答】(2)解: 点P(m,n)为线段AB上任意一点,经过(1)的平移后,在线段A'B'上对应的点P'的坐标为(m+5,n+2).
故答案为:(m+5,n+2).
【分析】(1)利用方格纸的特点分别将点A、B向上平移2个单位,再向右平移5个单位得到对应点A'、B',再连接即可;
(2)根据点的坐标的平移规律“左减右加,上加下减”可直接得出点P'的坐标.
21.【分析】(1)根据三角形面积求法得出即可;
(2)根据已知将△ABC各顶点向下平移2个单位,向右平移5个单位得到各对应点,即可作图;进而得出点C′的坐标.
【解答】解:(1)△ABC的面积是:×3×5=7.5;
(2)作图如下:
∴点C′的坐标为:(1,1).
【点评】此题主要考查了平移变换以及三角形面积求法,正确平移图象的各顶点坐标是解题关键.
22.解:(1)如图所示,点A坐标为(-4,3);
(2)∵A(-4,3),B(-1,3)
∴线段AB上任意一点的坐标可表示为(x,3)(-4≤x≤-1).
(3)由图可得S△ABP=3S△ABC=,
P点坐标为(0,m),则
解得或9
所以P点坐标为(0,9)或(0,-3).
23.(1)如图,△A1B1C1即为所求,B1的坐标(2,﹣2);
(2)△ABC的面积=3×52×23×31×5=6;
(3)如图,点D的坐标为(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
故答案为:(﹣5,3)或(0,2)或(5,1)或(﹣1,﹣5).
24.(1)C(-2,0),D(4,0)
(2)t=2
(3)值不变,为6
www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
