沪教版七年级数学下册试题 第十四章 三角形单元综合提优练习-沪教版(含答案)
文档属性
| 名称 | 沪教版七年级数学下册试题 第十四章 三角形单元综合提优练习-沪教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 994.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 11:27:35 | ||
图片预览




文档简介
第十四章 三角形单元综合提优练习
一、单选题
1.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
2.直线与两坐标轴交于、两点,点在坐标轴上,若为等腰三角形,则满足条件的点最多有( )个
A.8 B.4 C.5 D.7
3.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,给出下列结论:①∠ABC=45°;②AD∥BE;③∠CAD=∠BCE;④△CEB≌△ADC;⑤.那么其中正确的有( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB,连接EF,有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC.其中正确的有( )
A.①②③④ B.②③ C.②③④ D.③④
5.如图,,点B和点C是对应顶点,,记,,将绕点A顺时针旋转,当时,与之间的数量关系为( )
A. B. C. D.
6.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B'C' B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
7.如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
8.如图,已知点B、C、E在一直线上,、都是等边三角形,联结和,与相交于点F,与相交于点G,下列说法不一定正确的是( )
A. B. C. D.
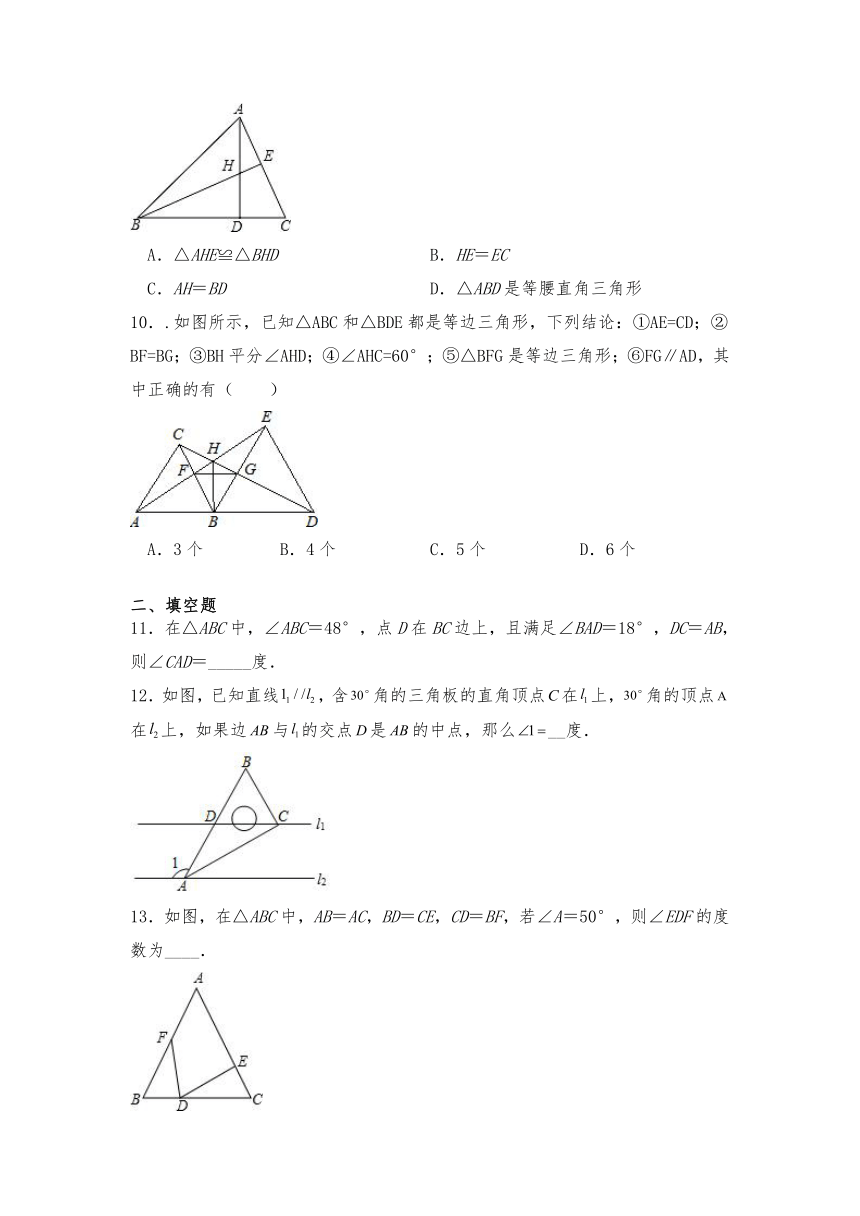
9.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H且HD=DC,那么下列结论中,正确的是( )
A.△AHE≌△BHD B.HE=EC
C.AH=BD D.△ABD是等腰直角三角形
10..如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.在△ABC中,∠ABC=48°,点D在BC边上,且满足∠BAD=18°,DC=AB,则∠CAD=_____度.
12.如图,已知直线,含角的三角板的直角顶点在上,角的顶点在上,如果边与的交点是的中点,那么__度.
13.如图,在△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF的度数为____.
14.在等腰△ABC中,如果过顶角顶点A的一条直线AD将△ABC分割成两个等腰三角形,那么∠BAC=___.
15.如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC等于___度.
16.如图,,,,给出下列结论:①;②;③;④;
其中正确的结论是__________________________________.(注:将你认为正确的结论填上)
17.在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于6,则△ABC的面积等于____.
18.如图,ABC的周长为26,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则DE的长是____.
19.已知:如图所示,等边三角形ABC,点P和Q分别从A和C两点同时出发,它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当点P在边AB上时,DE:AC=_________
20.如图,在中,,点在内,将以点为旋转中心进行旋转,使点B与点C重合,点M 落在点N处,若,且 B、M、N三点恰共线,则=_______.
三、解答题
21.如图,四边形ABCD中,AB=BC=3厘米,DA=DC=4厘米,∠DAB=∠DCB=90°,点P从A点开始沿射线AB方向运动,点Q从点C开始沿射线BC方向运动,P、Q两点运动速度均为1厘米/秒,两点同时运动.
(1)在P、Q两点运动过程中,请问∠PDQ的大小是否发生变化?请说明理由;
(2)当点P在线段AB上运动时(如图1),请求出四边形PDQB的而积;
(3)如图2,P点运动到AB延长线上,设DP与线段BC的交点为E.
①当P、Q运动了多少秒时,S△CDE=S△BPE.
②当P、Q运动了多少秒时,第①小问中两个三角形的面积差为(3﹣)平方厘米.
22.△ABC中,AC=BC,∠ACB=90°,点D是边BC上的一点,BE⊥AD交AD的延长线于点E,联结CE.
(1)如图,AD平分∠CAB,CF⊥CE交AD于点F,
①求证:AF=BE;
②直接写出∠BCE的度数,∠BCE=______°;
(2)如图,CM//BE交AD于点M,探究AM、ME与BE之间的数量关系:__________,并证明.
23.如图,在等边ABC中,AB=AC=BC=6cm,现有两点M、N分别从点A、B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次回到点B时,点M、N同时停止运动,设运动时间为t(s).
(1)当t= 时,M、N两点重合;
(2)当点M、N分别在AC、BA边上运动,AMN的形状会不断发生变化,当t= 时,AMN是等边三角形;
(3)当点M、N运动到BC边上时,若存在以MN为底边的等腰AMN,则t= .
24.△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠EAD=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.
(1)如图1,若∠EAD=∠BAC=60°,则△BEF是 三角形;
(2)若∠EAD=∠BAC≠60°:
①如图,当点D在线段BC上移动,判断△BEF的形状并证明;
②当点D在线段BC的延长线上移动,△BEF是什么三角形,请直接写出结论并画出相应的图形.
25.已知:如图,在四边形中,,点是边上一点,且平分,平分.
求证:(1);
(2)是线段的中点.
26.已知:如图所示,中,,D是AB上一点,DE⊥CD于D,交BC于E,且有.求证:
27.在△ABC中,AB=AC,点D是直线BC上的一点(不与点B、C重合),以AD为腰右侧作等腰三角形△ADE,且AD=AE,∠BAC=∠DAE,联接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度.
(2)设∠BAC=α,∠BCE=β.
①点D是在线段BC上移动时,如图2,则α、β之间有怎样的数量关系?试说明理由.
②点D是在射线CB上移动时,则α、β之间有怎样的数量关系?试直接写出结论.
28.如图,在△ABC中,∠A=90°,AB=AC,点D在射线AC上(点D不与点A重合)
(1)若点D在边AC时,延长AC至点G,CG=AD,过点D作DE⊥BD,交BC于点E,过G作HG⊥AG交DE延长线于点H.求证:BD=DH.
(2)过点A作AF⊥BD,垂足为F,射线AF交BC于点N,点Q在射线CA上,且∠QNC=∠ANB.求证:AQ=CD.
29.已知:如图,,AC平分∠MAB,BC平分∠NBA.过点C作直线DE,分别交AM、BN于D、E.
(1)求证:△ABC是直角三角形.
(2)求证:CD=CE.
30.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系,并说明理由.
答案
一、单选题
1.C
【思路指引】
根据等边三角形的性质和定义,可得:有一个角为60°的等腰三角形是等边三角形;三个内角都相等的三角形为等边三角形;再由中线的性质和三角形内角和的定义可解答本题.
【详解详析】
解:①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确;
②两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误;
③等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误;
④三个外角都相等的三角形是等边三角形,说法正确,
正确的命题有2个,
故选:C.
2.D
【思路指引】
运用分类讨论的数学思想,分AB为腰或底两种情况来分类解析,逐一判断,即可解决问题.
【详解详析】
解:如图,对于直线y=x 1,
当x=0时,y= 1;
当y=0时,x=1,
∴直线y=x 1与两个坐标轴的交点分别为A(0, 1),B(1,0);
若以点B为圆心,以AB的长为半径画弧,
则与x轴有两个交点,与y轴有一个交点(点A除外);
若以点A为圆心,以AB的长为半径画弧,
则与x轴有一个交点(点B除外),与y轴有两个交点;
∴以AB为腰的等腰△ABC有6个;
若以AB为底,作AB的垂直平分线,与坐标轴交于原点O,
综上所述,满足条件的点C最多有7个,
故选D.
3.D
【思路指引】
根据△ABC是等腰直角三角形可判断①正确;根据“内错角相等,两直线平行”可判断②正确;利用等腰三角形的性质及其它条件,证明△CEB≌△ADC,则其他结论易求.
【详解详析】
解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,故①正确;
∵BE⊥CE,AD⊥CE,
∴AD∥BE,故②正确;
∵∠BCE+∠ACD=90°∠ACD+∠CAD=90°
∴∠BCE=∠CAD,故③正确;
又∠E=∠ADC=90°,AC=BC
∴△CEB≌△ADC,故④正确
∴CE=AD,BE=CD
∴,故⑤正确.
因此,正确的结论有5个,
故选:D.
4.C
【思路指引】
利用旋转性质可得△ABF≌△ACD,根据全等三角形的性质一一判断即可.
【详解详析】
解:∵△ADC绕A顺时针旋转90°后得到△AFB,
∴△ABF≌△ACD,
∴∠BAF=∠CAD,AF=AD,BF=CD,故②④正确,
∴∠EAF=∠BAF+∠BAE=∠CAD+∠BAE=∠BAC﹣∠DAE=90°﹣45°=45°=∠DAE故③正确
无法判断BE=CD,故①错误,
故选:C.
5.C
【思路指引】
根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【详解详析】
解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°-α),
∵BC∥OA,
∴∠OBC=180°-∠O=180°-90°=90°,
∴β+(180°-α)=90°,
整理得,α=2β.
故选:C.
6.C
【思路指引】
根据全等三角形的判定定理进行推理.
【详解详析】
解:A、由AB=A′B′,AC=A′C′,BC=B'C'可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故选:C.
7.B
【思路指引】
根据题目中的条件和各个选项中的条件,利用全等三角形的判定方法,可以得到哪个选项中的条件,不能判定△ABE≌△ACD,从而可以解答本题.
【详解详析】
解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
8.B
【思路指引】
利用等边三角形的性质和“SAS”证明可得A选项;可利用“ASA”证明可得C、D选项,利用排除法求解即可.
【详解详析】
解:∵、都是等边三角形,
∴,=60°,,
∴∠ACB+∠ACD=∠ECD+∠ACD,即∠ACE=∠BCD,
∴(SAS),
∴BD=AE,(故A正确);
∴∠AEC=∠BDC,又,,
∴(ASA),
∴EG=FD,(故C正确),
FC=GC,(故D正确)
由于B项不能由已知条件得到,故B错误,
故选:B.
9.D
【思路指引】
首先根据垂直可得∠ADB=∠ADC=90°,然后再证明∠HAE=∠HBD,然后再利用AAS证明△ADC≌△BDH.
【详解详析】
解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴△ABD是等腰直角三角形,
故选:D.
10.D
【详解详析】
∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故选D.
二、填空题
11.66
【思路指引】
作辅助线,构建等腰三角形ABE,证明AB=BE,再证明△ABD≌△ACE,得∠CAE=∠BAD=18°,根据角的和可得结论.
【详解详析】
解:如图,在线段CD上取一点E,使CE=BD,连接AE,
∴CE+DE=BD+DE,
即CD=BE,
∵CD=AB,
∴AB=BE,
∴∠BAE=∠BEA,
∵∠B=48°,
∴∠BAE=∠BEA=66°,
∵∠B=48°,∠BAD=18°,
∴∠ADE=66°=∠AED,
∴AD=AE,∠ADB=∠AEC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠EAC=∠BAD=18°,
∴∠CAD=∠CAE+∠DAE=∠BAD+∠DAE=66°.
故答案为:66.
12.120
【思路指引】
根据直角三角形斜边上的中线性质得到,则,再利用三角形外角性质得到,然后根据平行线的性质求的度数.
【详解详析】
解:是斜边的中点,
,
,
,
,
,
.
故答案为120.
13.65°
【思路指引】
根据等腰三角形的性质可得出∠B=∠C及∠B的度数,结合BD=CE、BF=CD,即可证出△BDF≌△CED(SAS),由全等三角形的性质可得出∠CDE=∠BFD,再根据三角形内角和定理及平角等于180°,即可得出∠EDF=∠B,此题得解.
【详解详析】
解:∵AB=AC,∠A=50°,
∴∠B=∠C=(180°﹣∠A)=65°.
在△BDF和△CED中,,
∴△BDF≌△CED(SAS),
∴∠CDE=∠BFD.
∵∠BDF+∠BFD+∠B=180°,∠BDF+∠EDF+∠CDE=180°,
∴∠EDF=∠B=65°.
故答案为:65°
14.90°或108°.
【思路指引】
根据题意画出图形,分类讨论,利用三角形的内角和定理和等腰三角形的性质可得结论.
【详解详析】
解:①当BD=AD,CD=AD时,如图①所示,
∵AB=AC,
∴∠B=∠C,
设∠B=∠C=x,
∵BD=AD,CD=AD,
∴∠BAD=∠B=x,∠CAD=∠C=x,
∴4x=180°,
∴x=45°,
∴∠BAC=2x=45°×2=90°;
②当AD=BD,AC=CD时,如图②所示,
∵AB=AC,
∴∠B=∠C
设∠B=∠C=x,
∵AD=BD,AC=CD,
∴∠BAD=∠B=x,∠CAD=,
∴+x=180°-2x,
解得:x=36°,
∴∠BAC=180°-2x=180°-2×36°=108°,
故答案为:90°或108°.
15.45
【思路指引】
根据同角的余角相等求出∠CAD=∠HBD,再利用“角角边”证明△ACD和△BHD全等,根据全等三角形对应边相等可得AD=BD,然后判断出△ABD是等腰直角三角形,根据等腰直角三角形的性质解答即可.
【详解详析】
解:∵AD、BE是△ABC的高,
∴∠CAD+∠C=∠HBD+∠C,
∴∠CAD=∠HBD,
在△ACD和△BHD中,
,
∴△ACD≌△BHD(AAS),
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABC=45.
故答案为:45.
16.①②③
【思路指引】
利用三角形的内角和定理可判断①,证明可判断②,证明可判断③,最后证明可得 但是不能得到 从而可判断④.
【详解详析】
解: ,,
故①正确,符合题意;
,,,
故②正确,符合题意;
故③正确,符合题意;
但是不一定成立,故④错误,不符合题意;
故答案为:①②③
17.12
【思路指引】
先根据点O是△ABC的重心得出OD=AD,再由△BOD的面积等于6,得出S△ABD =S△BCE=18,即可求出SΔCEOD.
【详解详析】
解:∵△ABC中,中线AD、BE相交于点O,
∴点O是△ABC的重心,
∴OD=AD.
∵S△BOD=6,
∴S△ABD=18=S△ABC= S△BCE
∴S四边形CEOD= S△BCE - S△BOD =18 6=12.
故答案为:12.
18.6
【思路指引】
证明△BQA≌△BQE,得到BA=BE,同理证明△CAP≌△CDP,得到AC=CD,根据三角形的周长公式出去BE+CD,求出DE,
【详解详析】
解:∵BQ平分∠ABC,BQ⊥AE,
在△BQA和△BQE中,
,
∴△BQA≌△BQE,
∴BA=BE,
同理可证△CAP≌△CDP,得到AC=CD,
∵BE+CD=AB+AC=26-BC=26-10=16,
∴DE=BE+CD-BC=6,
故答案为:6
19.1:2
【思路指引】
延长AC,过点Q作垂直于AC的延长线于点F,证明,得到,又由,得到;证明,得到,即,从而得到结果.
【详解详析】
解:延长AC,过点Q作垂直于AC的延长线于点F,如下图:
∵
∴
又∵
∴
∴
∵点P和Q分别从A和C两点同时出发且速度相同
∴
∵△ABC是等边三角形
∴
又∵
∴
在和中,
∴
∴
∴
即:
在和中,
∴
∴
∴
∴
故答案为:
20.40°
【思路指引】
由全等可推理得到,由可得到,又由,结合三角形内角和定理即可求得答案.
【详解详析】
解:由旋转可知:
∴,
∴
即:
又∵
∴
∵
∴
∵
∴
∵
∴
故答案为:
三、解答题
21.
解:(1)∠PDQ的大小不发生变化,
理由是:∵∠A=∠DCB=∠DCQ=90°,由已知得出AP=CQ,
∴在△DAP和△DCQ中,
,
∴△DAP≌△DCQ(SAS),
∴∠ADP=∠CDQ,
∴∠PDQ=∠PDC+∠CDQ=∠PDC+∠ADP=∠ADC,
即∠PDQ的大小不发生变化,总等于∠ADC;
(2)∵△ADP≌△DCQ,
∴S△ADP=S△DCQ,
∴四边形PDQB的面积是:
S四边形PDQB=S四边形PDCB+S△CDQ
=S四边形PDCB+S△ADP
=S四边形ABCD
=×3×4+×3×4
=12(平方厘米);
(2)①连接BD,
设P、Q运动了t秒时,S△CDE=S△BPE,
∵S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB=0,
∵AB=BC=3,AP=t,DA=DC=4,
×3×4-×(t-3)×4=0,
解得t=6,
即P、Q运动了6秒时,S△CDE=S△BPE;
②连接BD,
设P、Q运动了t秒时,S△CDE-S△BPE=3-(平方厘米),
∴AP=CQ=t,
∴S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB,或S△BPE-S△CDE=S△PDB-S△DCB,
∵AB=BC=3,AP=t,DA=DC=4,
∴S△DCB=×3×4=6,S△PDB=×(t-3)×4=2(t-3),
∴S△CDE-S△BPE=S△DCB-S△PDB=6-2(t-3)=3-.
解得(秒),
或S△BPE-S△CDE=S△PDB-S△DCB=2(t-3)-6=3-.
解得(秒),
综上,当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
22.
(1)①证明:∵BE⊥AD,
∴∠ACB=∠BED=90°,
又∵∠ADC=∠BDE,
∴∠CAF=∠CBE,
∵CE⊥CF,
∴∠ECF=∠ACB=90°,
∴∠ACF=∠BCE,
又∵AC=BC,
∴△CAF≌△CBE(ASA),
∴AF=BE;
②∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°,
∵AD平分∠CAB,
∴∠CAF=∠BAD==22.5,
∵△CAF≌△CBE,
∴∠CBE=∠CAF=22.5,CE=CF,
∵CF⊥CE,
∴∠CFE=∠CEF=45°,
∴∠CEB=135°,
∴∠BCE=180°-135°-22.5=22.5,
故答案为:22.5;
(2)AM=BE+ME.理由如下:
作CG⊥CE交AD于点G,
∵BE⊥AD,
∴∠ACB=∠BED=90°,
又∵∠ADC=∠BDE,
∴∠CAG=∠CBE,
∵CE⊥CG,
∴∠ECG=∠ACB=90°,
∴∠ACG=∠BCE,
又∵AC=BC,
∴△CAG≌△CBE(ASA),
∴AG=BE,CG=CE,
∴△CGE是等腰直角三角形,
∵CM//BE,BE⊥AD,
∴CM⊥AD,
∴GM=ME,
∴AM=AG+GM=BE+ME.
23.
解:(1)设点M、N运动x秒后,M、N两点重合,
x+6=2x,
解得:x=6,
即当M、N运动6秒时,点N追上点M;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图1,
AM=t,AN=6-2t,
∵∠A=60°,当AM=AN时,△AMN是等边三角形,
∴t=6-2t,
解得t=2,
∴点M、N运动2秒后,可得到等边三角形△AMN;
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知6秒时M、N两点重合,恰好在C处,
如图4,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
∴t-6=18-2t,
解得t=8,符合题意.
所以假设成立,当M、N运动8秒时,能得到以MN为底的等腰三角形.
24.
解:(1)∵AB=AC,AD=AE,∠EAD=∠BAC=60°,
∴△AED和△ABC为等边三角形,∠C=∠ABC=60°,∠EAB=∠DAC,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),
∴∠EBA=∠C=60°
∵EF∥BC,
∴∠EFB=∠ABC=60°
在△EFB中,∠EFB=∠EBA=60°,
∴△EFB为等边三角形.
故答案为:等边;
(2)①结论:△EFB为等腰三角形.
理由:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形,
∴∠C=∠ABC,∠EAB=∠DAC.
同法可证△EAB≌△DAC(SAS),
∴∠EBA=∠C
∵EF∥BC,
∴∠EFB=∠ABC
∴∠EFB=∠EBA,
∴△EFB为等腰三角形;
②图形如图3所示,结论:△BEF是等腰三角形.
理由:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形,
∴∠ACB=∠ABC,
∴∠EAB=∠DAC,
同法可证△EAB≌△DAC(SAS),
∴∠EBA=∠ACD,
∴∠EBF=∠ACB,
∵EF∥BC,
∴∠AFE=∠ABC,
∵∠ABC=∠ACB,
∴∠AFE=∠ACB,
在△EFB中,∠EBF=∠AFE,
∴△EFB为等腰三角形.
25.
解:(1),
,
又、分别平分、,
,
,
(2)如图,延长,交于,
,,
,
,
,且,
,
.
26.
证明:过A作AF⊥CD于F,如下图:
∵AC=AD,AF⊥CD
∴CF=CD,∠AFC=
∵
∴∠ACF+∠DCE=
又∵DE⊥CD
∴∠CDE=,∠DCE+∠CED=
∴∠ACF=∠CED,
在△ACF与△CED中,
∴△ACF≌△CED,
∴CF=DE
∴DE=CD.
27.
解:(1)如图1,∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC-∠DAC=∠DAE-∠DAC,∠B=∠ACB=∠AED=45°,
∴∠BAD=∠CAE;
在△BAD与△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∴∠BCE=∠ACB+∠ACE=90°,
故答案为:90;
(2)①如图2,α+β=180°;理由如下:
∵∠BAC=∠DAE,AB=AC,AD=AE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABC=∠ACE,β=∠BCE=∠ACE+∠ACB=∠ABC+∠ACB=180°-α,
∴α+β=180°;
②当D在CB的延长线时,α=β.
∵∠DAE=∠BAC,AB=AC,AD=AE,
∴∠BAC-∠DAE=∠DAE-∠DAE,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
而∠ABD=∠ACB+α,β=∠ACE-∠ACB,
∴β=∠ACB+α-∠ACB,
∴α=β.
28.
(1)证明:∵CG=AD,
∴CG+DC=AD+DC,
∴DG=AC=AB,
∵DE⊥BD,
∴∠BDE=∠A=90°,
∴∠ADB+∠GDH=∠ADB+∠ABD=90°,
∴∠ABD=∠GDH,
在△ABD和△GDH中,
,
∴△ABD≌△GDH(ASA),
∴BD=DH;
(2)证明:如图,过C作CE⊥AC交AN延长线于点E,
∴∠ECQ=90°,
∵∠BAC=90°,AB=AC,
∴∠ACB=45°,
∴∠ECN=45°,
∴∠QCN=∠ECN,
∵∠QNC=∠ANB.∠ENC=∠ANB.
∴∠QNC=∠ENC.
在△QNC和ENC中,
,
∴△QNC≌ENC(ASA),
∴CQ=CE,
∵AF⊥BD,
∴∠AFD=∠BAC=90°,
∴∠ADB+∠FAD=∠ADB+∠ABD,
∴∠ABD=∠FAD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(ASA),
∴AD=CE;
∵CQ=CE,
∴AD=CQ,
∴AD+DQ=CQ+CQ,
∴AQ=CD.
29.
证明:(1)∵,
∴∠MAB+∠ABN=180°,
又∵AC平分∠MAB,BC平分∠NBA,
∴∠ABC+∠CAB=(∠ABN+∠MAB)=90°,
∴∠ACB=180°﹣(∠ABC+∠CAB)=90°,
∴△ACB是直角三角形;
(2)延长,交AD于P.
∵
∴∠APB=∠EBC,
∵BC平分∠NBA,
AC平分∠MAB,
30.
证明:(1)如图1,∵E是AB的中点,
∴AE=BE,
∵ADBC,
∴∠A=∠ABF,∠ADE=∠F,
∴△ADE≌△BFE(AAS);
(2)答:如图2,EG垂直平分DF.
理由是:∵∠ADF=∠F,∠ADF=∠GDF,
∴∠F=∠GDF,
∴DG=FG,
由(1)得:△ADE≌△BFE,
∴DE=EF,
∴EG⊥FD;
一、单选题
1.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
2.直线与两坐标轴交于、两点,点在坐标轴上,若为等腰三角形,则满足条件的点最多有( )个
A.8 B.4 C.5 D.7
3.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,给出下列结论:①∠ABC=45°;②AD∥BE;③∠CAD=∠BCE;④△CEB≌△ADC;⑤.那么其中正确的有( )
A.2个 B.3个 C.4个 D.5个
4.如图所示,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB,连接EF,有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC.其中正确的有( )
A.①②③④ B.②③ C.②③④ D.③④
5.如图,,点B和点C是对应顶点,,记,,将绕点A顺时针旋转,当时,与之间的数量关系为( )
A. B. C. D.
6.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.BC=B'C' B.∠A=∠A′
C.∠C=∠C′ D.∠B=∠B′=90°
7.如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.OB=OC D.∠BDC=∠CEB
8.如图,已知点B、C、E在一直线上,、都是等边三角形,联结和,与相交于点F,与相交于点G,下列说法不一定正确的是( )
A. B. C. D.
9.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于点H且HD=DC,那么下列结论中,正确的是( )
A.△AHE≌△BHD B.HE=EC
C.AH=BD D.△ABD是等腰直角三角形
10..如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.在△ABC中,∠ABC=48°,点D在BC边上,且满足∠BAD=18°,DC=AB,则∠CAD=_____度.
12.如图,已知直线,含角的三角板的直角顶点在上,角的顶点在上,如果边与的交点是的中点,那么__度.
13.如图,在△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF的度数为____.
14.在等腰△ABC中,如果过顶角顶点A的一条直线AD将△ABC分割成两个等腰三角形,那么∠BAC=___.
15.如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC等于___度.
16.如图,,,,给出下列结论:①;②;③;④;
其中正确的结论是__________________________________.(注:将你认为正确的结论填上)
17.在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于6,则△ABC的面积等于____.
18.如图,ABC的周长为26,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则DE的长是____.
19.已知:如图所示,等边三角形ABC,点P和Q分别从A和C两点同时出发,它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当点P在边AB上时,DE:AC=_________
20.如图,在中,,点在内,将以点为旋转中心进行旋转,使点B与点C重合,点M 落在点N处,若,且 B、M、N三点恰共线,则=_______.
三、解答题
21.如图,四边形ABCD中,AB=BC=3厘米,DA=DC=4厘米,∠DAB=∠DCB=90°,点P从A点开始沿射线AB方向运动,点Q从点C开始沿射线BC方向运动,P、Q两点运动速度均为1厘米/秒,两点同时运动.
(1)在P、Q两点运动过程中,请问∠PDQ的大小是否发生变化?请说明理由;
(2)当点P在线段AB上运动时(如图1),请求出四边形PDQB的而积;
(3)如图2,P点运动到AB延长线上,设DP与线段BC的交点为E.
①当P、Q运动了多少秒时,S△CDE=S△BPE.
②当P、Q运动了多少秒时,第①小问中两个三角形的面积差为(3﹣)平方厘米.
22.△ABC中,AC=BC,∠ACB=90°,点D是边BC上的一点,BE⊥AD交AD的延长线于点E,联结CE.
(1)如图,AD平分∠CAB,CF⊥CE交AD于点F,
①求证:AF=BE;
②直接写出∠BCE的度数,∠BCE=______°;
(2)如图,CM//BE交AD于点M,探究AM、ME与BE之间的数量关系:__________,并证明.
23.如图,在等边ABC中,AB=AC=BC=6cm,现有两点M、N分别从点A、B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次回到点B时,点M、N同时停止运动,设运动时间为t(s).
(1)当t= 时,M、N两点重合;
(2)当点M、N分别在AC、BA边上运动,AMN的形状会不断发生变化,当t= 时,AMN是等边三角形;
(3)当点M、N运动到BC边上时,若存在以MN为底边的等腰AMN,则t= .
24.△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠EAD=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.
(1)如图1,若∠EAD=∠BAC=60°,则△BEF是 三角形;
(2)若∠EAD=∠BAC≠60°:
①如图,当点D在线段BC上移动,判断△BEF的形状并证明;
②当点D在线段BC的延长线上移动,△BEF是什么三角形,请直接写出结论并画出相应的图形.
25.已知:如图,在四边形中,,点是边上一点,且平分,平分.
求证:(1);
(2)是线段的中点.
26.已知:如图所示,中,,D是AB上一点,DE⊥CD于D,交BC于E,且有.求证:
27.在△ABC中,AB=AC,点D是直线BC上的一点(不与点B、C重合),以AD为腰右侧作等腰三角形△ADE,且AD=AE,∠BAC=∠DAE,联接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度.
(2)设∠BAC=α,∠BCE=β.
①点D是在线段BC上移动时,如图2,则α、β之间有怎样的数量关系?试说明理由.
②点D是在射线CB上移动时,则α、β之间有怎样的数量关系?试直接写出结论.
28.如图,在△ABC中,∠A=90°,AB=AC,点D在射线AC上(点D不与点A重合)
(1)若点D在边AC时,延长AC至点G,CG=AD,过点D作DE⊥BD,交BC于点E,过G作HG⊥AG交DE延长线于点H.求证:BD=DH.
(2)过点A作AF⊥BD,垂足为F,射线AF交BC于点N,点Q在射线CA上,且∠QNC=∠ANB.求证:AQ=CD.
29.已知:如图,,AC平分∠MAB,BC平分∠NBA.过点C作直线DE,分别交AM、BN于D、E.
(1)求证:△ABC是直角三角形.
(2)求证:CD=CE.
30.如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系,并说明理由.
答案
一、单选题
1.C
【思路指引】
根据等边三角形的性质和定义,可得:有一个角为60°的等腰三角形是等边三角形;三个内角都相等的三角形为等边三角形;再由中线的性质和三角形内角和的定义可解答本题.
【详解详析】
解:①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确;
②两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误;
③等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误;
④三个外角都相等的三角形是等边三角形,说法正确,
正确的命题有2个,
故选:C.
2.D
【思路指引】
运用分类讨论的数学思想,分AB为腰或底两种情况来分类解析,逐一判断,即可解决问题.
【详解详析】
解:如图,对于直线y=x 1,
当x=0时,y= 1;
当y=0时,x=1,
∴直线y=x 1与两个坐标轴的交点分别为A(0, 1),B(1,0);
若以点B为圆心,以AB的长为半径画弧,
则与x轴有两个交点,与y轴有一个交点(点A除外);
若以点A为圆心,以AB的长为半径画弧,
则与x轴有一个交点(点B除外),与y轴有两个交点;
∴以AB为腰的等腰△ABC有6个;
若以AB为底,作AB的垂直平分线,与坐标轴交于原点O,
综上所述,满足条件的点C最多有7个,
故选D.
3.D
【思路指引】
根据△ABC是等腰直角三角形可判断①正确;根据“内错角相等,两直线平行”可判断②正确;利用等腰三角形的性质及其它条件,证明△CEB≌△ADC,则其他结论易求.
【详解详析】
解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,故①正确;
∵BE⊥CE,AD⊥CE,
∴AD∥BE,故②正确;
∵∠BCE+∠ACD=90°∠ACD+∠CAD=90°
∴∠BCE=∠CAD,故③正确;
又∠E=∠ADC=90°,AC=BC
∴△CEB≌△ADC,故④正确
∴CE=AD,BE=CD
∴,故⑤正确.
因此,正确的结论有5个,
故选:D.
4.C
【思路指引】
利用旋转性质可得△ABF≌△ACD,根据全等三角形的性质一一判断即可.
【详解详析】
解:∵△ADC绕A顺时针旋转90°后得到△AFB,
∴△ABF≌△ACD,
∴∠BAF=∠CAD,AF=AD,BF=CD,故②④正确,
∴∠EAF=∠BAF+∠BAE=∠CAD+∠BAE=∠BAC﹣∠DAE=90°﹣45°=45°=∠DAE故③正确
无法判断BE=CD,故①错误,
故选:C.
5.C
【思路指引】
根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
【详解详析】
解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°-α),
∵BC∥OA,
∴∠OBC=180°-∠O=180°-90°=90°,
∴β+(180°-α)=90°,
整理得,α=2β.
故选:C.
6.C
【思路指引】
根据全等三角形的判定定理进行推理.
【详解详析】
解:A、由AB=A′B′,AC=A′C′,BC=B'C'可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故选:C.
7.B
【思路指引】
根据题目中的条件和各个选项中的条件,利用全等三角形的判定方法,可以得到哪个选项中的条件,不能判定△ABE≌△ACD,从而可以解答本题.
【详解详析】
解:∵∠ABC=∠ACB,
∴AB=AC,
∵∠BAE=∠CAD,
∴补充条件AD=AE时,△ABE≌△ACD(SAS),故选项A不符合题意;
补充条件BE=CD,无法判断△ABE≌△ACD,故选项B符合题意;
补充条件OB=OC时,则∠OBC=∠OCB,故∠ABE=∠ACD,则△ABE≌△ACD(ASA),故选项C不符合题意;
补充条件∠BDC=∠CEB时,则∠AEB=∠ADC,则△ABE≌△ACD(AAS),故选项D不符合题意;
故选:B.
8.B
【思路指引】
利用等边三角形的性质和“SAS”证明可得A选项;可利用“ASA”证明可得C、D选项,利用排除法求解即可.
【详解详析】
解:∵、都是等边三角形,
∴,=60°,,
∴∠ACB+∠ACD=∠ECD+∠ACD,即∠ACE=∠BCD,
∴(SAS),
∴BD=AE,(故A正确);
∴∠AEC=∠BDC,又,,
∴(ASA),
∴EG=FD,(故C正确),
FC=GC,(故D正确)
由于B项不能由已知条件得到,故B错误,
故选:B.
9.D
【思路指引】
首先根据垂直可得∠ADB=∠ADC=90°,然后再证明∠HAE=∠HBD,然后再利用AAS证明△ADC≌△BDH.
【详解详析】
解:∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∴∠DAE+∠AHE=90°,
∵BE⊥AC,
∴∠HBD+∠BHD=90°,
∵∠AHE=∠BHD,
∴∠HAE=∠HBD,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(AAS),
∴BD=AD,
∵∠BDA=90°,
∴△ABD是等腰直角三角形,
故选:D.
10.D
【详解详析】
∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故选D.
二、填空题
11.66
【思路指引】
作辅助线,构建等腰三角形ABE,证明AB=BE,再证明△ABD≌△ACE,得∠CAE=∠BAD=18°,根据角的和可得结论.
【详解详析】
解:如图,在线段CD上取一点E,使CE=BD,连接AE,
∴CE+DE=BD+DE,
即CD=BE,
∵CD=AB,
∴AB=BE,
∴∠BAE=∠BEA,
∵∠B=48°,
∴∠BAE=∠BEA=66°,
∵∠B=48°,∠BAD=18°,
∴∠ADE=66°=∠AED,
∴AD=AE,∠ADB=∠AEC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠EAC=∠BAD=18°,
∴∠CAD=∠CAE+∠DAE=∠BAD+∠DAE=66°.
故答案为:66.
12.120
【思路指引】
根据直角三角形斜边上的中线性质得到,则,再利用三角形外角性质得到,然后根据平行线的性质求的度数.
【详解详析】
解:是斜边的中点,
,
,
,
,
,
.
故答案为120.
13.65°
【思路指引】
根据等腰三角形的性质可得出∠B=∠C及∠B的度数,结合BD=CE、BF=CD,即可证出△BDF≌△CED(SAS),由全等三角形的性质可得出∠CDE=∠BFD,再根据三角形内角和定理及平角等于180°,即可得出∠EDF=∠B,此题得解.
【详解详析】
解:∵AB=AC,∠A=50°,
∴∠B=∠C=(180°﹣∠A)=65°.
在△BDF和△CED中,,
∴△BDF≌△CED(SAS),
∴∠CDE=∠BFD.
∵∠BDF+∠BFD+∠B=180°,∠BDF+∠EDF+∠CDE=180°,
∴∠EDF=∠B=65°.
故答案为:65°
14.90°或108°.
【思路指引】
根据题意画出图形,分类讨论,利用三角形的内角和定理和等腰三角形的性质可得结论.
【详解详析】
解:①当BD=AD,CD=AD时,如图①所示,
∵AB=AC,
∴∠B=∠C,
设∠B=∠C=x,
∵BD=AD,CD=AD,
∴∠BAD=∠B=x,∠CAD=∠C=x,
∴4x=180°,
∴x=45°,
∴∠BAC=2x=45°×2=90°;
②当AD=BD,AC=CD时,如图②所示,
∵AB=AC,
∴∠B=∠C
设∠B=∠C=x,
∵AD=BD,AC=CD,
∴∠BAD=∠B=x,∠CAD=,
∴+x=180°-2x,
解得:x=36°,
∴∠BAC=180°-2x=180°-2×36°=108°,
故答案为:90°或108°.
15.45
【思路指引】
根据同角的余角相等求出∠CAD=∠HBD,再利用“角角边”证明△ACD和△BHD全等,根据全等三角形对应边相等可得AD=BD,然后判断出△ABD是等腰直角三角形,根据等腰直角三角形的性质解答即可.
【详解详析】
解:∵AD、BE是△ABC的高,
∴∠CAD+∠C=∠HBD+∠C,
∴∠CAD=∠HBD,
在△ACD和△BHD中,
,
∴△ACD≌△BHD(AAS),
∴AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABC=45.
故答案为:45.
16.①②③
【思路指引】
利用三角形的内角和定理可判断①,证明可判断②,证明可判断③,最后证明可得 但是不能得到 从而可判断④.
【详解详析】
解: ,,
故①正确,符合题意;
,,,
故②正确,符合题意;
故③正确,符合题意;
但是不一定成立,故④错误,不符合题意;
故答案为:①②③
17.12
【思路指引】
先根据点O是△ABC的重心得出OD=AD,再由△BOD的面积等于6,得出S△ABD =S△BCE=18,即可求出SΔCEOD.
【详解详析】
解:∵△ABC中,中线AD、BE相交于点O,
∴点O是△ABC的重心,
∴OD=AD.
∵S△BOD=6,
∴S△ABD=18=S△ABC= S△BCE
∴S四边形CEOD= S△BCE - S△BOD =18 6=12.
故答案为:12.
18.6
【思路指引】
证明△BQA≌△BQE,得到BA=BE,同理证明△CAP≌△CDP,得到AC=CD,根据三角形的周长公式出去BE+CD,求出DE,
【详解详析】
解:∵BQ平分∠ABC,BQ⊥AE,
在△BQA和△BQE中,
,
∴△BQA≌△BQE,
∴BA=BE,
同理可证△CAP≌△CDP,得到AC=CD,
∵BE+CD=AB+AC=26-BC=26-10=16,
∴DE=BE+CD-BC=6,
故答案为:6
19.1:2
【思路指引】
延长AC,过点Q作垂直于AC的延长线于点F,证明,得到,又由,得到;证明,得到,即,从而得到结果.
【详解详析】
解:延长AC,过点Q作垂直于AC的延长线于点F,如下图:
∵
∴
又∵
∴
∴
∵点P和Q分别从A和C两点同时出发且速度相同
∴
∵△ABC是等边三角形
∴
又∵
∴
在和中,
∴
∴
∴
即:
在和中,
∴
∴
∴
∴
故答案为:
20.40°
【思路指引】
由全等可推理得到,由可得到,又由,结合三角形内角和定理即可求得答案.
【详解详析】
解:由旋转可知:
∴,
∴
即:
又∵
∴
∵
∴
∵
∴
∵
∴
故答案为:
三、解答题
21.
解:(1)∠PDQ的大小不发生变化,
理由是:∵∠A=∠DCB=∠DCQ=90°,由已知得出AP=CQ,
∴在△DAP和△DCQ中,
,
∴△DAP≌△DCQ(SAS),
∴∠ADP=∠CDQ,
∴∠PDQ=∠PDC+∠CDQ=∠PDC+∠ADP=∠ADC,
即∠PDQ的大小不发生变化,总等于∠ADC;
(2)∵△ADP≌△DCQ,
∴S△ADP=S△DCQ,
∴四边形PDQB的面积是:
S四边形PDQB=S四边形PDCB+S△CDQ
=S四边形PDCB+S△ADP
=S四边形ABCD
=×3×4+×3×4
=12(平方厘米);
(2)①连接BD,
设P、Q运动了t秒时,S△CDE=S△BPE,
∵S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB=0,
∵AB=BC=3,AP=t,DA=DC=4,
×3×4-×(t-3)×4=0,
解得t=6,
即P、Q运动了6秒时,S△CDE=S△BPE;
②连接BD,
设P、Q运动了t秒时,S△CDE-S△BPE=3-(平方厘米),
∴AP=CQ=t,
∴S△CDE=S△DCB-S△DEB,S△BPE=S△PDB-S△DEB,
∴S△CDE-S△BPE=S△DCB-S△PDB,或S△BPE-S△CDE=S△PDB-S△DCB,
∵AB=BC=3,AP=t,DA=DC=4,
∴S△DCB=×3×4=6,S△PDB=×(t-3)×4=2(t-3),
∴S△CDE-S△BPE=S△DCB-S△PDB=6-2(t-3)=3-.
解得(秒),
或S△BPE-S△CDE=S△PDB-S△DCB=2(t-3)-6=3-.
解得(秒),
综上,当秒或秒时,S△BPE与S△CDE的差为(3﹣)平方厘米.
22.
(1)①证明:∵BE⊥AD,
∴∠ACB=∠BED=90°,
又∵∠ADC=∠BDE,
∴∠CAF=∠CBE,
∵CE⊥CF,
∴∠ECF=∠ACB=90°,
∴∠ACF=∠BCE,
又∵AC=BC,
∴△CAF≌△CBE(ASA),
∴AF=BE;
②∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°,
∵AD平分∠CAB,
∴∠CAF=∠BAD==22.5,
∵△CAF≌△CBE,
∴∠CBE=∠CAF=22.5,CE=CF,
∵CF⊥CE,
∴∠CFE=∠CEF=45°,
∴∠CEB=135°,
∴∠BCE=180°-135°-22.5=22.5,
故答案为:22.5;
(2)AM=BE+ME.理由如下:
作CG⊥CE交AD于点G,
∵BE⊥AD,
∴∠ACB=∠BED=90°,
又∵∠ADC=∠BDE,
∴∠CAG=∠CBE,
∵CE⊥CG,
∴∠ECG=∠ACB=90°,
∴∠ACG=∠BCE,
又∵AC=BC,
∴△CAG≌△CBE(ASA),
∴AG=BE,CG=CE,
∴△CGE是等腰直角三角形,
∵CM//BE,BE⊥AD,
∴CM⊥AD,
∴GM=ME,
∴AM=AG+GM=BE+ME.
23.
解:(1)设点M、N运动x秒后,M、N两点重合,
x+6=2x,
解得:x=6,
即当M、N运动6秒时,点N追上点M;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图1,
AM=t,AN=6-2t,
∵∠A=60°,当AM=AN时,△AMN是等边三角形,
∴t=6-2t,
解得t=2,
∴点M、N运动2秒后,可得到等边三角形△AMN;
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知6秒时M、N两点重合,恰好在C处,
如图4,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
∴t-6=18-2t,
解得t=8,符合题意.
所以假设成立,当M、N运动8秒时,能得到以MN为底的等腰三角形.
24.
解:(1)∵AB=AC,AD=AE,∠EAD=∠BAC=60°,
∴△AED和△ABC为等边三角形,∠C=∠ABC=60°,∠EAB=∠DAC,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),
∴∠EBA=∠C=60°
∵EF∥BC,
∴∠EFB=∠ABC=60°
在△EFB中,∠EFB=∠EBA=60°,
∴△EFB为等边三角形.
故答案为:等边;
(2)①结论:△EFB为等腰三角形.
理由:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形,
∴∠C=∠ABC,∠EAB=∠DAC.
同法可证△EAB≌△DAC(SAS),
∴∠EBA=∠C
∵EF∥BC,
∴∠EFB=∠ABC
∴∠EFB=∠EBA,
∴△EFB为等腰三角形;
②图形如图3所示,结论:△BEF是等腰三角形.
理由:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴△AED和△ABC为等腰三角形,
∴∠ACB=∠ABC,
∴∠EAB=∠DAC,
同法可证△EAB≌△DAC(SAS),
∴∠EBA=∠ACD,
∴∠EBF=∠ACB,
∵EF∥BC,
∴∠AFE=∠ABC,
∵∠ABC=∠ACB,
∴∠AFE=∠ACB,
在△EFB中,∠EBF=∠AFE,
∴△EFB为等腰三角形.
25.
解:(1),
,
又、分别平分、,
,
,
(2)如图,延长,交于,
,,
,
,
,且,
,
.
26.
证明:过A作AF⊥CD于F,如下图:
∵AC=AD,AF⊥CD
∴CF=CD,∠AFC=
∵
∴∠ACF+∠DCE=
又∵DE⊥CD
∴∠CDE=,∠DCE+∠CED=
∴∠ACF=∠CED,
在△ACF与△CED中,
∴△ACF≌△CED,
∴CF=DE
∴DE=CD.
27.
解:(1)如图1,∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAC-∠DAC=∠DAE-∠DAC,∠B=∠ACB=∠AED=45°,
∴∠BAD=∠CAE;
在△BAD与△CAE中,,
∴△BAD≌△CAE(SAS),
∴∠B=∠ACE,
∴∠BCE=∠ACB+∠ACE=90°,
故答案为:90;
(2)①如图2,α+β=180°;理由如下:
∵∠BAC=∠DAE,AB=AC,AD=AE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABC=∠ACE,β=∠BCE=∠ACE+∠ACB=∠ABC+∠ACB=180°-α,
∴α+β=180°;
②当D在CB的延长线时,α=β.
∵∠DAE=∠BAC,AB=AC,AD=AE,
∴∠BAC-∠DAE=∠DAE-∠DAE,
∴∠BAD=∠CAE;
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
而∠ABD=∠ACB+α,β=∠ACE-∠ACB,
∴β=∠ACB+α-∠ACB,
∴α=β.
28.
(1)证明:∵CG=AD,
∴CG+DC=AD+DC,
∴DG=AC=AB,
∵DE⊥BD,
∴∠BDE=∠A=90°,
∴∠ADB+∠GDH=∠ADB+∠ABD=90°,
∴∠ABD=∠GDH,
在△ABD和△GDH中,
,
∴△ABD≌△GDH(ASA),
∴BD=DH;
(2)证明:如图,过C作CE⊥AC交AN延长线于点E,
∴∠ECQ=90°,
∵∠BAC=90°,AB=AC,
∴∠ACB=45°,
∴∠ECN=45°,
∴∠QCN=∠ECN,
∵∠QNC=∠ANB.∠ENC=∠ANB.
∴∠QNC=∠ENC.
在△QNC和ENC中,
,
∴△QNC≌ENC(ASA),
∴CQ=CE,
∵AF⊥BD,
∴∠AFD=∠BAC=90°,
∴∠ADB+∠FAD=∠ADB+∠ABD,
∴∠ABD=∠FAD,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(ASA),
∴AD=CE;
∵CQ=CE,
∴AD=CQ,
∴AD+DQ=CQ+CQ,
∴AQ=CD.
29.
证明:(1)∵,
∴∠MAB+∠ABN=180°,
又∵AC平分∠MAB,BC平分∠NBA,
∴∠ABC+∠CAB=(∠ABN+∠MAB)=90°,
∴∠ACB=180°﹣(∠ABC+∠CAB)=90°,
∴△ACB是直角三角形;
(2)延长,交AD于P.
∵
∴∠APB=∠EBC,
∵BC平分∠NBA,
AC平分∠MAB,
30.
证明:(1)如图1,∵E是AB的中点,
∴AE=BE,
∵ADBC,
∴∠A=∠ABF,∠ADE=∠F,
∴△ADE≌△BFE(AAS);
(2)答:如图2,EG垂直平分DF.
理由是:∵∠ADF=∠F,∠ADF=∠GDF,
∴∠F=∠GDF,
∴DG=FG,
由(1)得:△ADE≌△BFE,
∴DE=EF,
∴EG⊥FD;
