甘肃省宁县第五中学人教版高中数学必修四1-5函数yAsinωx+φ的图象 课件(共16张PPT)
文档属性
| 名称 | 甘肃省宁县第五中学人教版高中数学必修四1-5函数yAsinωx+φ的图象 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 850.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-07 15:37:23 | ||
图片预览




文档简介
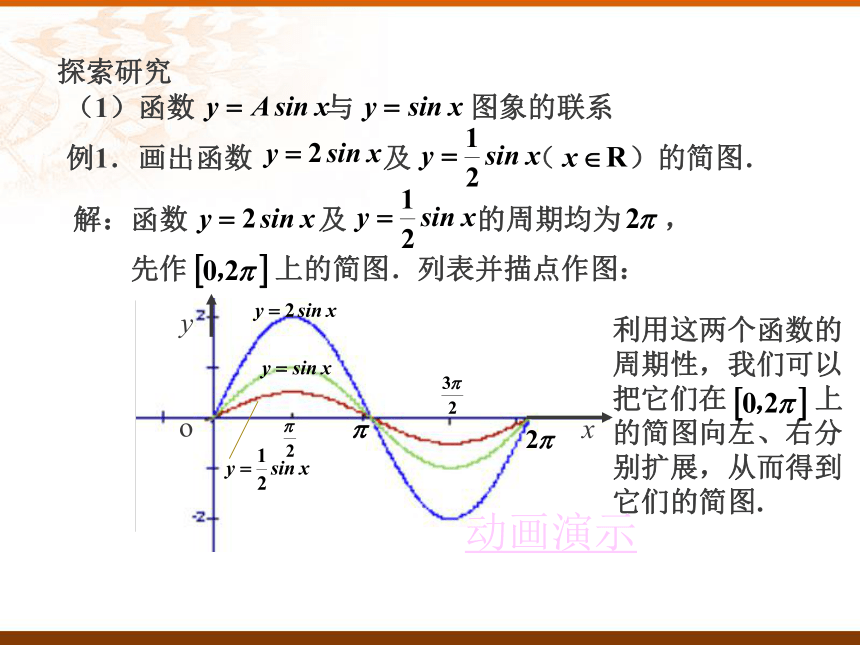
课件16张PPT。欢迎各位领导、老师莅临指导!执教:崔新宇 1.5 函数 的图像探索研究 (1)函数 与 图象的联系 例1.画出函数 及 ( )的简图. 解:函数 及 的周期均为 ,先作 上的简图. 列表并描点作图: 0100000000-1-22利用这两个函数的
周期性,我们可以
把它们在 上
的简图向左、右分
别扩展,从而得到
它们的简图.归纳总结: 函数 ( 且 )的图像可以看做是把函数 的图像上所有点的纵坐标伸长(当 时)或缩短(当 )到原来的 倍(横坐标不变)而得到,这种变换称为振幅变换,它是由 的变化而引起的, 叫做函数 的振幅.
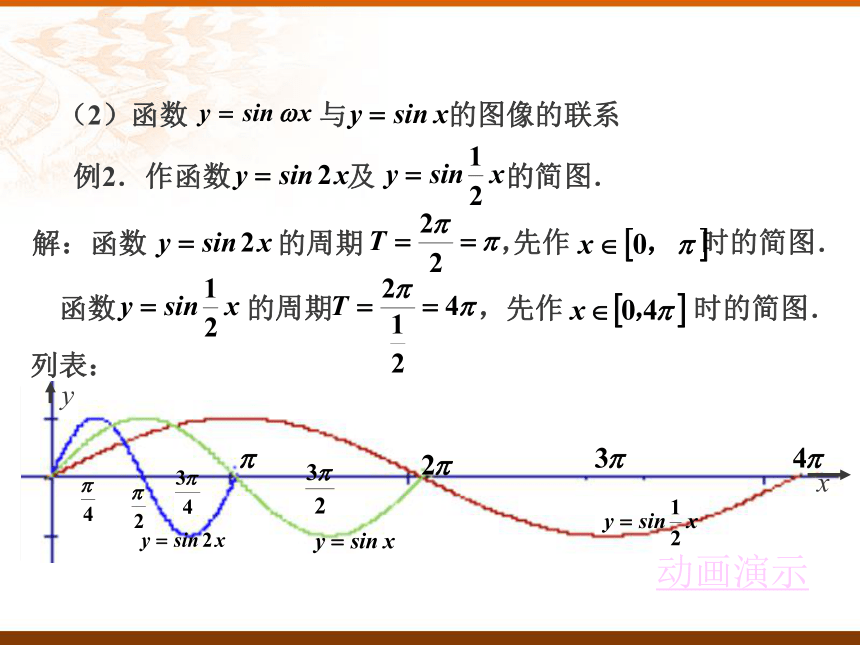
, 的值域是 ,最大值是 ,最小值是 . (2)函数 与 的图像的联系 例2.作函数 及 的简图. 解:函数 的周期 , 先作 时的简图. 列表: 000000001-11-1函数 的周期 ,先作 时的简图. 动画演示归纳总结: 函数 ( 且 )的图像,可以看做是把
的图像上所有点的横坐标缩短(当 时)或伸长(当 时)到原来的 倍(纵坐标不变)而得到的.这种变换称为周期变换,它是由 的变化而引起的, 与周期 的关系为 . 利用这两个函数的周期性,把各函数一个周期的简图向左、右分别扩展,从而得到它们的简图.1.画出下列函数在长为一周期的闭区间上的简图
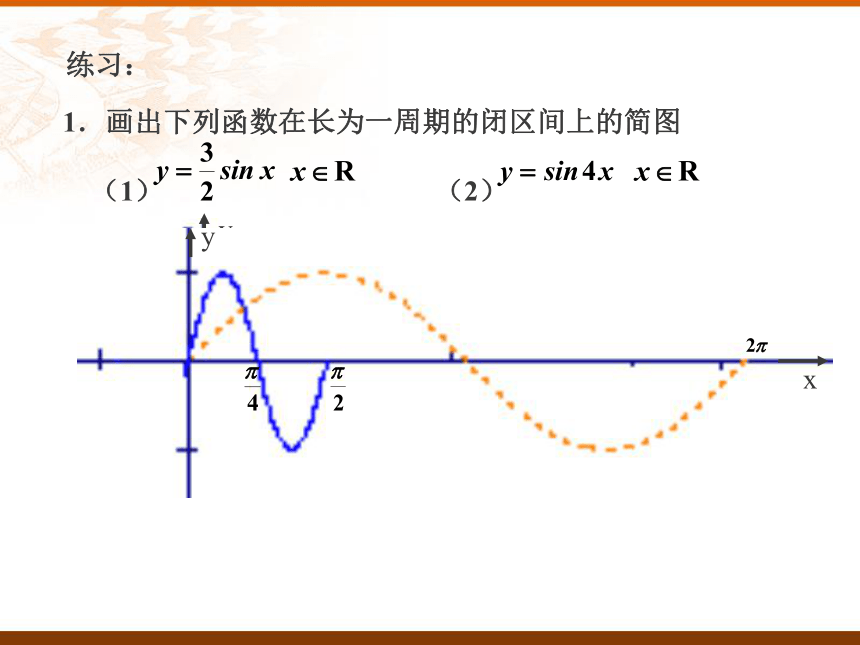
(1) (2)练习: 周期是 ,把 的图像上每个点的横坐标伸长 倍
(纵坐标不变)即得 的图像. 2.函数 , 的周期是什么?它的图像与正弦
曲线有什么联系.3.说明如何由 ;由 的图像沿轴方向压缩 得 的图像(纵坐标
不变);把 的图像上纵坐标缩短 倍(横坐标不变),即得 的图像. [例3]画出函数 y=sin(x+ ),x∈R
y=sin(x-),x∈R 的简图.解:列表X=x+ sin(x+) 0 2 - 010-10(3)函数y=sin(x+φ)与 y=sinx的图像的联系动画演示 ≠0)的图
象,可以看作把正弦曲线上所有点向左(当 >0时)或向右 <0时)平行移动||个单位长度而得到.归纳总结:(当堂上练习1.若将某函数的图象向右平移 以后所得到的图象的
函数式是y=sin(x+ ),则原来的函数表达式为 ----------------
y=sin(x+) 2.若函数f(x)=sin2x+acos2x的图象关于直线x=- 对
称,求:a的值. 分析:这是已知函数图象的对称轴方程,求函数解析式中参数值的一类逆向型题,解题的关键是如何巧用对称性.提示:∵x1=0,x2=-是定义域中关于x=- 对称的两点
∴f(0)=f(- )答案:-13.若对任意实数a,函数y=5sin(πx - )
(k∈N)在区间[a,a+3]上的值 出现不少于4次
且不多于8次,求k的值。 分析:这也是求函数解析式中参数值的逆向型题,解题的思路是:先求出与k相关的周期T的取值范围,再求k.答案:k=2或3.又因每一周期内出现 值时有2次,出现4次取2个周期,
出现 值8次应有4个周期.
∴有4T≥3且2T≤3作业布置必做P57no:2、3(ω=1)
选做p70no:18
课外作业:配套练习册谢谢各位老师光临!
周期性,我们可以
把它们在 上
的简图向左、右分
别扩展,从而得到
它们的简图.归纳总结: 函数 ( 且 )的图像可以看做是把函数 的图像上所有点的纵坐标伸长(当 时)或缩短(当 )到原来的 倍(横坐标不变)而得到,这种变换称为振幅变换,它是由 的变化而引起的, 叫做函数 的振幅.
, 的值域是 ,最大值是 ,最小值是 . (2)函数 与 的图像的联系 例2.作函数 及 的简图. 解:函数 的周期 , 先作 时的简图. 列表: 000000001-11-1函数 的周期 ,先作 时的简图. 动画演示归纳总结: 函数 ( 且 )的图像,可以看做是把
的图像上所有点的横坐标缩短(当 时)或伸长(当 时)到原来的 倍(纵坐标不变)而得到的.这种变换称为周期变换,它是由 的变化而引起的, 与周期 的关系为 . 利用这两个函数的周期性,把各函数一个周期的简图向左、右分别扩展,从而得到它们的简图.1.画出下列函数在长为一周期的闭区间上的简图
(1) (2)练习: 周期是 ,把 的图像上每个点的横坐标伸长 倍
(纵坐标不变)即得 的图像. 2.函数 , 的周期是什么?它的图像与正弦
曲线有什么联系.3.说明如何由 ;由 的图像沿轴方向压缩 得 的图像(纵坐标
不变);把 的图像上纵坐标缩短 倍(横坐标不变),即得 的图像. [例3]画出函数 y=sin(x+ ),x∈R
y=sin(x-),x∈R 的简图.解:列表X=x+ sin(x+) 0 2 - 010-10(3)函数y=sin(x+φ)与 y=sinx的图像的联系动画演示 ≠0)的图
象,可以看作把正弦曲线上所有点向左(当 >0时)或向右 <0时)平行移动||个单位长度而得到.归纳总结:(当堂上练习1.若将某函数的图象向右平移 以后所得到的图象的
函数式是y=sin(x+ ),则原来的函数表达式为 ----------------
y=sin(x+) 2.若函数f(x)=sin2x+acos2x的图象关于直线x=- 对
称,求:a的值. 分析:这是已知函数图象的对称轴方程,求函数解析式中参数值的一类逆向型题,解题的关键是如何巧用对称性.提示:∵x1=0,x2=-是定义域中关于x=- 对称的两点
∴f(0)=f(- )答案:-13.若对任意实数a,函数y=5sin(πx - )
(k∈N)在区间[a,a+3]上的值 出现不少于4次
且不多于8次,求k的值。 分析:这也是求函数解析式中参数值的逆向型题,解题的思路是:先求出与k相关的周期T的取值范围,再求k.答案:k=2或3.又因每一周期内出现 值时有2次,出现4次取2个周期,
出现 值8次应有4个周期.
∴有4T≥3且2T≤3作业布置必做P57no:2、3(ω=1)
选做p70no:18
课外作业:配套练习册谢谢各位老师光临!
