4.9《表面积的变化》(第一课时)(教学课件)五年级 数学下册 沪教版(共23张PPT)
文档属性
| 名称 | 4.9《表面积的变化》(第一课时)(教学课件)五年级 数学下册 沪教版(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
表面积的变化
小学数学·五年级(下)
沪教版·第四单元
第一课时
让学生通过把几个相同的正方体或长方体拼成较大的长方体的操作活动,探索并发现拼接前后有关几何体表面积的变化规律。
应用发现的规律解决一些简单实际问题。
培养学生的合作能力、空间想象能力和思维能力。
重
经过动手操作,增强学生的空间观念,能运用知识解决生活中的数学问题。
通过操作,比较拼成的长方体的表面积与原来两个正方体的表面积的和究竟发生了什么变化,发现规律。
棱长是1厘米的正方体,体积和表面积分别是多少呢?
1cm
V=1×1×1=1(cm3)
S=6×(1×1)=6(cm2)
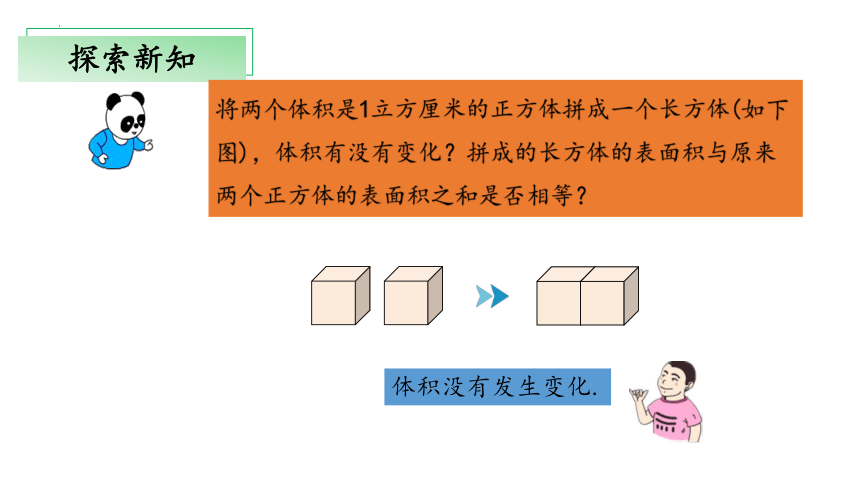
将两个体积是1立方厘米的正方体拼成一个长方体(如下图),体积有没有变化?拼成的长方体的表面积与原来两个正方体的表面积之和是否相等?
体积没有发生变化.
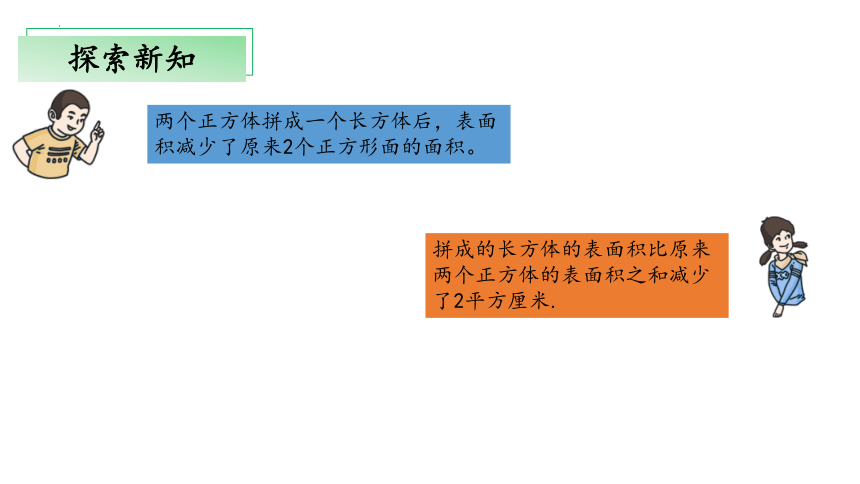
两个正方体拼成一个长方体后,表面积减少了原来2个正方形面的面积。
拼成的长方体的表面积比原来两个正方体的表面积之和减少了2平方厘米.
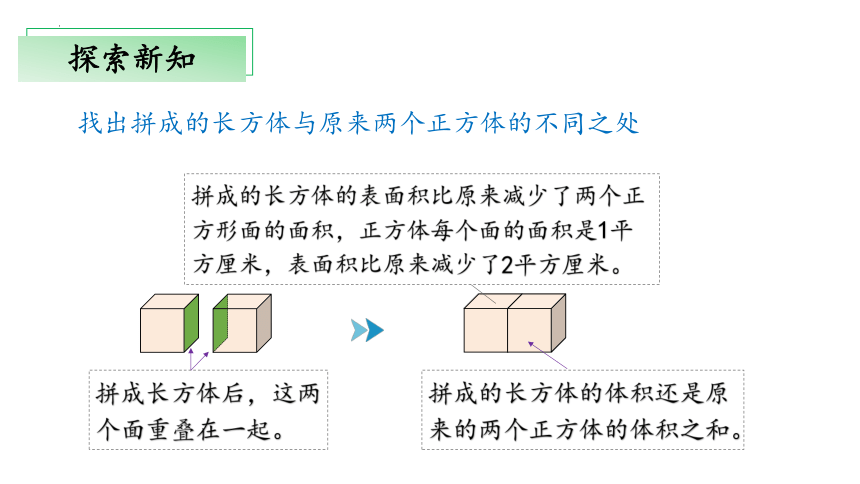
找出拼成的长方体与原来两个正方体的不同之处
拼成长方体后,这两
个面重叠在一起。
拼成的长方体的体积还是原
来的两个正方体的体积之和。
拼成的长方体的表面积比原来减少了两个正方形面的面积,正方体每个面的面积是1平方厘米,表面积比原来减少了2平方厘米。
将两个体积是1立方厘米的正方体拼成一个长方体,体积没有变化;拼成的长方体的表面积与原来两个正方体的表面积之和不相等,表面积比原来两个正方形面的面积和减少了2平方厘米。
正确解答
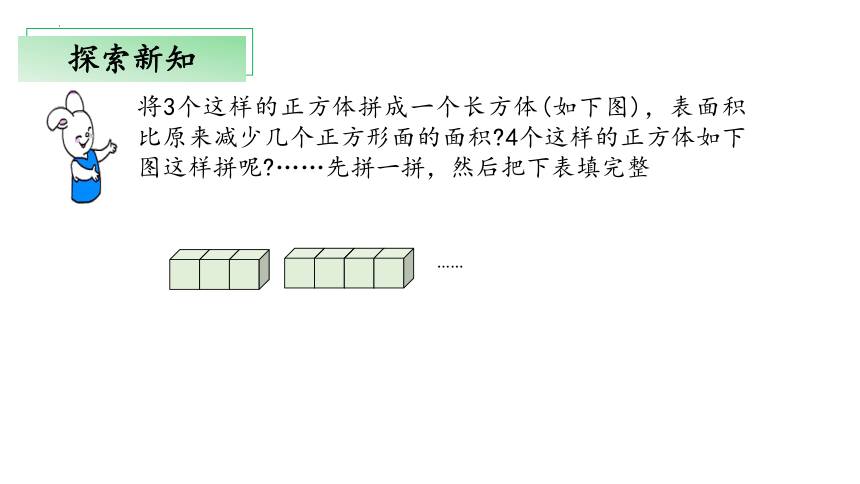
将3个这样的正方体拼成一个长方体(如下图),表面积比原来减少几个正方形面的面积 4个这样的正方体如下图这样拼呢 ……先拼一拼,然后把下表填完整
……
正方体的个数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
2
3
4
5
……
……
……
……
从表中你发现什么规律?
摆一摆,填一填,找出表面积的变化规律。
……
减少4个正方形面的面积。
减少6个正方形面的面积。
减少8个正方形面的面积。
正方体的个数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
2
3
4
5
……
……
……
……
2
12
10
14
4
18
18
6
24
22
8
30
发现:2个正方体拼成一个长方体,减少2个正方形面;
3个正方体拼成一个长方体,减少4个正方形面……
摆一摆,填一填,找出表面积的变化规律
规律:
(1)将若干个相同的正方体摆成一排拼成一个长方体,每增加1个正方体,拼成长方体后就减少了原来2个正方形面的面积,即减少的正方形面的个数=(正方体的个数-1)×2;
(2)拼成的长方体的表面积=原来正方体的表面积之和-拼成长方体后减少的正方形面的面积。
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
2×2=4 (cm )
2×2=4 (个)
2×2=4 (cm ) 4×4=16 (cm )
√
2cm
……减少面的个数
……每个面的大小
……减少的面积
=2×(12+12+4)
=2×28
=56 (cm )
=4×12+2×4
=48+8
=56 (cm )
6cm
2cm
2cm
4×(6×2)+2×(2×2)
2×(6×2+6×2+2×2)
=6×4×3-16
=72-16
=56 (cm )
拼成长方体后表面积是多少平方厘米?
减少了16cm
6×(2×2)×3-16
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
=2×(12+12+4)
=2×28
=56 (cm )
=4×12+2×4
=48+8
=56 (cm )
4×(6×2)+2×(2×2)
2×(6×2+6×2+2×2)
=6×4×3-16
=72-16
=56 (cm )
减少了16cm
6×(2×2)×3-16
=14×4
=56 (cm )
14×(2×2)
拼成长方体后表面积是多少平方厘米?
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
将若干个相同的正方体拼成一个长方体,体积不发生变化,表面积发生变化。
相同的正方体摆成一排拼成一个长方体,减少的正方形面的个数=(正方体的个数-1)×2;拼成的长方体的表面积=原来正方体的表面积之和-拼成长方体后减少的正方形面的面积。
1
2
A的表面积:
拼接以后减少了14个面。
B的表面积,
拼接以后减少了10个面。
所以:
A的表面积<B的表面积
1.如图,用6个体积是1立方分米的正方体可以拼成A、B两个不同的长方体,哪个长方体的表面积大
锯了3次,增加6个面。
C
拼了2次,减少4个面;
2×2×4=16(平方厘米)
B
2.选择。(把正确答案的编号填在括号里)(1)如图,把一根长方体木块锯成4段,比原来共增加了( )个面的面积
(2)用3个棱长为2厘米的小正方体木块拼成一个长方体,表面积会减少( )平方厘米。
A. 3 B.4 C.6 D.8
解:切割以后增加了4个面,
增加的表面积:
3.6÷3=1.2(分米)
1.2×1.2×4
=1.44×4
=5.76(平方分米)
答:表面积增加了5.76平方分米。
3.如图,把一个长为 3.6 分米的长方体刚好切成了3个大小相等的正方体。这3个正方体的表面积的总和比原来这个长方体的表面积增加了多少平方分米
解:
体积:
V=10×10×10-1×1×1
=1000-1
=999(立方厘米)
表面积:
S=6×(10×10)
=6×100
=600(平方厘米)
答:剩余立体图形的体积是999立方厘米;表面积不变。
4.如图,在棱长为 10 厘米的正方体的一个顶角处挖去一个棱长为1厘米的正方体。剩余的立体图形的体积是多少立方厘米 表面积怎样变化
解:
切割之后增加的大正方形面数:2×3=6(个)
每个大正方形面的面积:516÷6=86(平方厘米)
增加的表面积:86×6=516(平方厘米)
答:切割后增加的表面积是516平方厘米。
5.如图,把一个表面积是 516 平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米
设计一个长方体纸箱,正好能装下24个棱长是1分米的正方体小纸盒,怎样设计材料最省?
Thank you!
表面积的变化
小学数学·五年级(下)
沪教版·第四单元
第一课时
让学生通过把几个相同的正方体或长方体拼成较大的长方体的操作活动,探索并发现拼接前后有关几何体表面积的变化规律。
应用发现的规律解决一些简单实际问题。
培养学生的合作能力、空间想象能力和思维能力。
重
经过动手操作,增强学生的空间观念,能运用知识解决生活中的数学问题。
通过操作,比较拼成的长方体的表面积与原来两个正方体的表面积的和究竟发生了什么变化,发现规律。
棱长是1厘米的正方体,体积和表面积分别是多少呢?
1cm
V=1×1×1=1(cm3)
S=6×(1×1)=6(cm2)
将两个体积是1立方厘米的正方体拼成一个长方体(如下图),体积有没有变化?拼成的长方体的表面积与原来两个正方体的表面积之和是否相等?
体积没有发生变化.
两个正方体拼成一个长方体后,表面积减少了原来2个正方形面的面积。
拼成的长方体的表面积比原来两个正方体的表面积之和减少了2平方厘米.
找出拼成的长方体与原来两个正方体的不同之处
拼成长方体后,这两
个面重叠在一起。
拼成的长方体的体积还是原
来的两个正方体的体积之和。
拼成的长方体的表面积比原来减少了两个正方形面的面积,正方体每个面的面积是1平方厘米,表面积比原来减少了2平方厘米。
将两个体积是1立方厘米的正方体拼成一个长方体,体积没有变化;拼成的长方体的表面积与原来两个正方体的表面积之和不相等,表面积比原来两个正方形面的面积和减少了2平方厘米。
正确解答
将3个这样的正方体拼成一个长方体(如下图),表面积比原来减少几个正方形面的面积 4个这样的正方体如下图这样拼呢 ……先拼一拼,然后把下表填完整
……
正方体的个数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
2
3
4
5
……
……
……
……
从表中你发现什么规律?
摆一摆,填一填,找出表面积的变化规律。
……
减少4个正方形面的面积。
减少6个正方形面的面积。
减少8个正方形面的面积。
正方体的个数
拼成长方体后减少了原来几个面的面积
原来正方体的表面积之和(cm2)
拼成的长方体的表面积(cm2)
2
3
4
5
……
……
……
……
2
12
10
14
4
18
18
6
24
22
8
30
发现:2个正方体拼成一个长方体,减少2个正方形面;
3个正方体拼成一个长方体,减少4个正方形面……
摆一摆,填一填,找出表面积的变化规律
规律:
(1)将若干个相同的正方体摆成一排拼成一个长方体,每增加1个正方体,拼成长方体后就减少了原来2个正方形面的面积,即减少的正方形面的个数=(正方体的个数-1)×2;
(2)拼成的长方体的表面积=原来正方体的表面积之和-拼成长方体后减少的正方形面的面积。
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
2×2=4 (cm )
2×2=4 (个)
2×2=4 (cm ) 4×4=16 (cm )
√
2cm
……减少面的个数
……每个面的大小
……减少的面积
=2×(12+12+4)
=2×28
=56 (cm )
=4×12+2×4
=48+8
=56 (cm )
6cm
2cm
2cm
4×(6×2)+2×(2×2)
2×(6×2+6×2+2×2)
=6×4×3-16
=72-16
=56 (cm )
拼成长方体后表面积是多少平方厘米?
减少了16cm
6×(2×2)×3-16
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
=2×(12+12+4)
=2×28
=56 (cm )
=4×12+2×4
=48+8
=56 (cm )
4×(6×2)+2×(2×2)
2×(6×2+6×2+2×2)
=6×4×3-16
=72-16
=56 (cm )
减少了16cm
6×(2×2)×3-16
=14×4
=56 (cm )
14×(2×2)
拼成长方体后表面积是多少平方厘米?
把棱长为2厘米的3个正方体拼成一个长方体(如下图).拼成的长方体表面积比原来3个正方体的表面积之和减少了多少平方厘米?
将若干个相同的正方体拼成一个长方体,体积不发生变化,表面积发生变化。
相同的正方体摆成一排拼成一个长方体,减少的正方形面的个数=(正方体的个数-1)×2;拼成的长方体的表面积=原来正方体的表面积之和-拼成长方体后减少的正方形面的面积。
1
2
A的表面积:
拼接以后减少了14个面。
B的表面积,
拼接以后减少了10个面。
所以:
A的表面积<B的表面积
1.如图,用6个体积是1立方分米的正方体可以拼成A、B两个不同的长方体,哪个长方体的表面积大
锯了3次,增加6个面。
C
拼了2次,减少4个面;
2×2×4=16(平方厘米)
B
2.选择。(把正确答案的编号填在括号里)(1)如图,把一根长方体木块锯成4段,比原来共增加了( )个面的面积
(2)用3个棱长为2厘米的小正方体木块拼成一个长方体,表面积会减少( )平方厘米。
A. 3 B.4 C.6 D.8
解:切割以后增加了4个面,
增加的表面积:
3.6÷3=1.2(分米)
1.2×1.2×4
=1.44×4
=5.76(平方分米)
答:表面积增加了5.76平方分米。
3.如图,把一个长为 3.6 分米的长方体刚好切成了3个大小相等的正方体。这3个正方体的表面积的总和比原来这个长方体的表面积增加了多少平方分米
解:
体积:
V=10×10×10-1×1×1
=1000-1
=999(立方厘米)
表面积:
S=6×(10×10)
=6×100
=600(平方厘米)
答:剩余立体图形的体积是999立方厘米;表面积不变。
4.如图,在棱长为 10 厘米的正方体的一个顶角处挖去一个棱长为1厘米的正方体。剩余的立体图形的体积是多少立方厘米 表面积怎样变化
解:
切割之后增加的大正方形面数:2×3=6(个)
每个大正方形面的面积:516÷6=86(平方厘米)
增加的表面积:86×6=516(平方厘米)
答:切割后增加的表面积是516平方厘米。
5.如图,把一个表面积是 516 平方厘米的正方体切割成8个相等的小正方体(无剩余,损耗不计),切割后的8个小正方体的表面积之和比原来大正方体的表面积增加多少平方厘米
设计一个长方体纸箱,正好能装下24个棱长是1分米的正方体小纸盒,怎样设计材料最省?
Thank you!
