第五单元 面积(复习课件)-三年级数学下学期期末核心考点集训(北师大版)(共24张PPT)
文档属性
| 名称 | 第五单元 面积(复习课件)-三年级数学下学期期末核心考点集训(北师大版)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 15:00:43 | ||
图片预览






文档简介
(共24张PPT)
第五单元 面积
三年级下册 北师大版
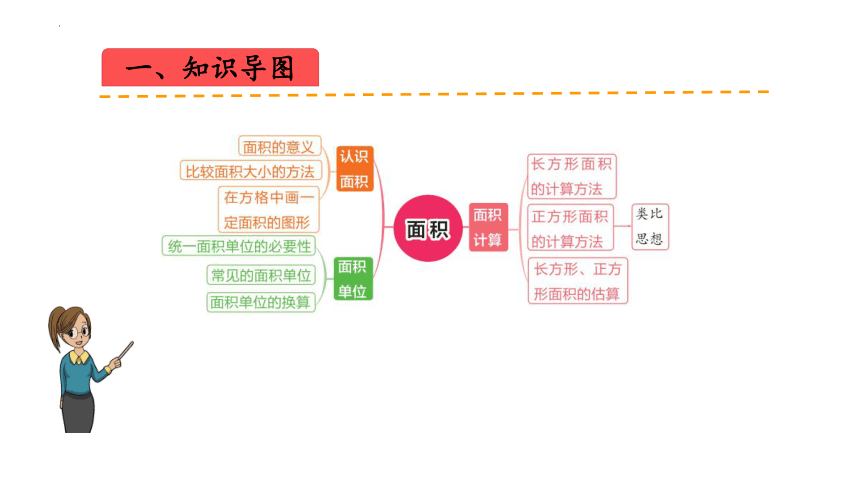
一、知识导图
二、考点梳理
知识点① 比较面积大小的方法
1.观察法;2.重叠法;3.摆小正方形法。
二、考点梳理
知识点② 常见的面积单位
1.平方厘米:边长是1厘米的正方形面积是1平方厘米;
2.平方分米:边长是1分米的正方形面积是1平方分米;
3.平方米:边长是1米的正方形面积是1平方米。
二、考点梳理
知识点③ 面积单位的换算
1平方米=100平方分米,1平方分米=100平方厘米。
二、考点梳理
知识点④ 面积的计算
长方形的面积公式:长方形的面积=长x宽;正方形的面积公式:正方形的面积=边
长x边长。
三、典例精讲
分析
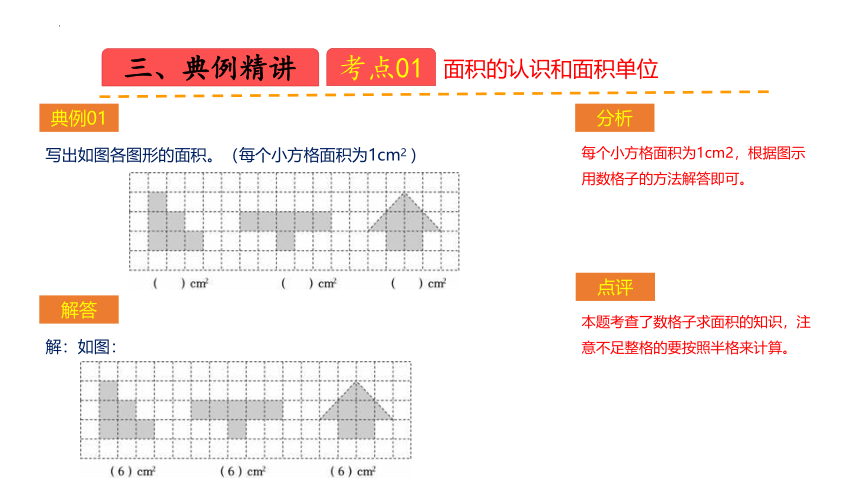
典例01
每个小方格面积为1cm2,根据图示
用数格子的方法解答即可。
面积的认识和面积单位
考点01
解答
点评
本题考查了数格子求面积的知识,注
意不足整格的要按照半格来计算。
写出如图各图形的面积。(每个小方格面积为1cm2 )
解:如图:
三、典例精讲
分析
变式①
面积的认识和面积单位
考点01
物体的表面或围成的平面图形的大小,叫做它们的面积,也就是说面积
就是平面图形的大小。你知道如图各个图形的面积各是多少吗?
左边图形中有15个 ,面积是15个的
面积和。中间图形中有14个 和4
个半格,面积等于(14+4÷2)个 的
面积和。右边图形中有24个 和6个
半格,面积等于(24+6÷2)个 的
面积和。
三、典例精讲
点评
解答
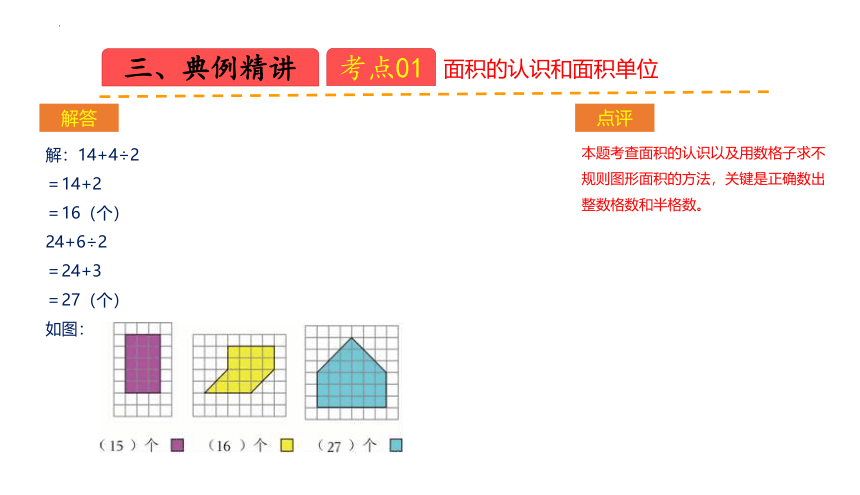
本题考查面积的认识以及用数格子求不
规则图形面积的方法,关键是正确数出
整数格数和半格数。
面积的认识和面积单位
考点01
解:14+4÷2
=14+2
=16(个)
24+6÷2
=24+3
=27(个)
如图:
三、典例精讲
分析
变式②
(1)4平方分米=400平方厘米,40平方厘米<400平方厘米.
(2)9平方米=90000平方厘米,90000平方厘米>900平方厘米.
(3)5平方米=500平方分米,150平方分米<500平方分米.
(4)8平方分米=800平方厘米,790平方厘米<800平方厘米.
(5)低级单位平方厘米化高级单位平方分米除以进率100,即2100平方厘米=21平方分米.
(6)99平方分米=9900平方厘米,600平方厘米<9900平方厘米.
面积的认识和面积单位
考点01
在〇里填上“>““<”或“=”.
40平方厘米〇4平方分米 9平方米〇900平方厘米
150平方分米〇5平方米 790平方厘米〇8平方分米
2100平方厘米〇21平方分米 600平方厘米〇99平方分米
三、典例精讲
点评
解答
不同单位的名数的大小比较通常是先
化成相同的单位名数,再根据数值的
大小进行比较.平方米、平方分米、
平方厘米相邻单位间的进率是100,
由高级单位化低级单位乘进率,反之
除以进率.
面积的认识和面积单位
考点01
解:
故答案为:<,>,<,<,=,<.
(1)40平方厘米<4平方分米 (2)9平方米>900平方厘米
(3)150平方分米<5平方米 (4)790平方厘米<8平方分米
(5)2100平方厘米=21平方分米 (6)600平方厘米<99平方分米
三、典例精讲
分析
变式③
分别算出每个图形是由多少个小正方形组成的,再比
较即可。
(1)①号是有3个正方形和4个三角形组成的,2个三角形的面
积等于1个正方形的面积,所以①号的面积是5个正方形的面积;
②号的面积是6个正方形的面积;③号是有4个正方形和2个三
角形组成的,2个三角形的面积等于1个正方形的面积,所以③
号的面积是5个正方形的面积;④号是有2个正方形和2个底是2
个格,高是1个格的三角形组成的,这2个三角形的面积等于2
个正方形的面积,所以④号的面积是4个正方形的面积;⑤号
的面积是2个正方形的面积;⑥号的面积是2个三角形的面积,
等于1个正方形的面积;(2)①号是有3个正方形和4个三角形
组成的,2个三角形的面积等于1个正方形的面积,所以①号的
面积是5个正方形的面积;③号是有4个正方形和2个三角形组
成的,2个三角形的面积等于1个正方形的面积,所以③号的面
积是5个正方形的面积;(3)⑥号的面积是2个三角形的面积,
即1个正方形的面积,据此解答即可。
面积的认识和面积单位
考点01
看图填一填。
(1) 号图形的面积最大,是 个 。
(2) 号图形和 号图形的面积相等,是 个 。
(3) 号图形的面积最小,是 个 。
三、典例精讲
点评
解答
本题考查的是面积的认识和大小比较
知识的运用,灵活运用所学的知识是
解答本题的关键。
面积的认识和面积单位
考点01
解:根据分析可知:6>5>4>2>1,即:
(1)②号图形的面积最大,是6个 。
(2)①号图形和③号图形的面积相等,是5个 。
(3)⑥号图形的面积最小,是1个 。
故答案为:(1)②;6;(2)①;③;5;(3)⑥;1。
三、典例精讲
分析
典例02
(1)5平方分米=500平方厘米,500平方厘米>490平方厘米.
(2)24平方米=2400平方厘米.
(3)800平方分米=8平方米,8平方米<9平方米.
(4)1000平方分米=10平方米,10平方米<100平方米.
小面积单位间的进率及单位换算
考点02
填上“>”、“<”或“=”.
5平方分米 490平方厘米
24平方米 2400平方分米
800平方分米 9平方米
1000平方分米 100平方米.
三、典例精讲
点评
解答
不同单位的名数的大小比较通常是先
化成相同的单位名数,再根据整数或
小数或分数的大小比较方法进行比较.
化成什么单位要灵活掌握.
小面积单位间的进率及单位换算
考点02
解:(1)5平方分米>490平方厘米;
(2)24平方米=2400平方分米;
(3)800平方分米<9平方米;
(4)1000平方分<100平方米.
故答案为:>,=,<,<.
三、典例精讲
分析
变式①
根据长方形的面积计算公式“长方形
面积=长×宽”,求出走廊的面积是
多少平方米,然后把平方米化成平方
分米;再根据正方形的面积公式“正
方形面积=边长×边长”求出地砖的
面积,然后用走廊的面积除以正方形
地砖的面积,即可得到需要的块数。
小面积单位间的进率及单位换算
考点02
解答
点评
此题考查的知识点:长方形面积的计
算、正方形面积的计算、面积的单位
换算、整数除法的应用。
解:60米=600分米,2米=20分米
(600×20)÷(2×2)
=12000÷4
=3000(块)
答:需要3000块方砖。
实验小学要在教学楼的一条走廊里铺方砖,这条走廊长60米、宽2米,
用边长2分米的正方形方砖铺地,需要多少块方砖?
三、典例精讲
分析
变式②
(1)5平方分米=500平方厘米,50平方
厘米<500平方厘米,即50平方厘米<5
平方分米.(2)60平方米=6000平方分
米,6000平方分米>60平方分米,即60
平方米>60平方分米.(3)7平方分米=
700平方厘米,780平方厘米>700平方厘
米,即780平方厘米>7平方分米.(4)
低级单位平方分米化高级单位平方米除以
进率100,即400平方分米=4平方米.
小面积单位间的进率及单位换算
考点02
在〇里填上“>”“<”或“=”.
50平方厘米〇5平方分米
60平方米〇60平方分米
780平方厘米〇7平方分米
400平方分米〇4平方米
点评
解答
不同单位的名数的大小比较通常是先化成
相同的单位名数,再根据数值的大小进行
比较.
解:(1)50平方厘米<5平方分米
(2)60平方米>60平方分米
(3)780平方厘米>7平方分米
(4)400平方分米=4平方米.
故答案为:<,>,>,=.
三、典例精讲
分析
变式③
根据正方形的面积=边长×边长求出
面积是多少平方分米,然后根据1平
方米=100平方分米进行判断即可。
小面积单位间的进率及单位换算
考点02
我们已经学习了“1m2=100dm2”,这个关系是如何推导出来的呢?
请你用文字、画图或计算说明推导过程。
点评
解答
本题考查了平方米和平方分米之间的
关系推导过程。
解:如果正方形的边长是1米,面积就是1×1=1(平方米)
因为1米=10分米,所以10×10=100(平方分米),因此1平方米=
100平方分米。
三、典例精讲
分析
典例03
根据平移的知识,剩下部分的面积等
于大正方形的面积减去小长方形的面
积。
长方形、正方形的面积
考点03
解答
解:10×10﹣6×4
=100﹣24
=76(平方厘米)
答:剩下部分的面积是76平方厘米。
点评
熟练掌握长方形和正方形面积公式,
是解答此题的关键。
如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米
的长方形,剩下部分的面积是多少?
三、典例精讲
分析
变式①
长方形的面积=长×宽,则长方形的长
为400÷8=50(米),扩大后的绿地
宽为32米,长不变,据此计算出扩大
后长方形的面积即可。
长方形、正方形的面积
考点03
解答
解:400÷8=50(米)
50×32=1600(平方米)
答:扩大后的绿地面积是1600平方米。
点评
本题考查了长方形面积公式的灵活运
用,结合题意分析解答即可。
如图,一块长方形绿地面积为400平方米,如果长不变,宽增加到32米,
扩大后的绿地面积是多少平方米?
三、典例精讲
分析
变式②
长方形的长=面积÷宽,现在的宽是
6+24=30(米),根据长方形面积
=长×宽,可求出扩建后的面积。
长方形、正方形的面积
考点03
解答
点评
此题考查长方形面积公式的灵活应用。
解:180÷6=30(米)
6+24=30(米)
30×30=900(平方米)
答:扩建后菜地的面积是900平方米。
王爷爷家有一块长方形菜地(如图),面积是180平方米。现在准备扩
建,长不变,宽增加了24米。扩建后菜地的面积是多少平方米?
三、典例精讲
分析
变式③
根据题意可知,可以围成边长是1厘
米、边长是5厘米、边长是(5+1)
厘米、边长是8厘米、边长是(8+1)
厘米、边长是(5+8)厘米、边长是
(1+5+8)厘米的正方形,根据正
方形的面积=边长×边长,把数据代
入公式解答。
长方形、正方形的面积
考点03
有8厘米、5厘米和1厘米长的小棒各4根,从中选出若干根,并使它们首
尾相接,你能围成多少种大小不同的正方形?围成正方形的面积分别是
多少?请在下表列举不同的围法。
边长/厘米
面积/平方厘米
三、典例精讲
点评
解答
此题考查的目的是理解掌握正方形的
特征及应用,正方形的面积公式及应
用,关键是熟记公式。
长方形、正方形的面积
考点03
解:1+5=6(厘米)
1+8=9(厘米)
5+8=13(厘米)
1+5+8=14(厘米)
答:一共有7种不同的围法。
填表如下:
谢谢观看~
第五单元 面积
三年级下册 北师大版
一、知识导图
二、考点梳理
知识点① 比较面积大小的方法
1.观察法;2.重叠法;3.摆小正方形法。
二、考点梳理
知识点② 常见的面积单位
1.平方厘米:边长是1厘米的正方形面积是1平方厘米;
2.平方分米:边长是1分米的正方形面积是1平方分米;
3.平方米:边长是1米的正方形面积是1平方米。
二、考点梳理
知识点③ 面积单位的换算
1平方米=100平方分米,1平方分米=100平方厘米。
二、考点梳理
知识点④ 面积的计算
长方形的面积公式:长方形的面积=长x宽;正方形的面积公式:正方形的面积=边
长x边长。
三、典例精讲
分析
典例01
每个小方格面积为1cm2,根据图示
用数格子的方法解答即可。
面积的认识和面积单位
考点01
解答
点评
本题考查了数格子求面积的知识,注
意不足整格的要按照半格来计算。
写出如图各图形的面积。(每个小方格面积为1cm2 )
解:如图:
三、典例精讲
分析
变式①
面积的认识和面积单位
考点01
物体的表面或围成的平面图形的大小,叫做它们的面积,也就是说面积
就是平面图形的大小。你知道如图各个图形的面积各是多少吗?
左边图形中有15个 ,面积是15个的
面积和。中间图形中有14个 和4
个半格,面积等于(14+4÷2)个 的
面积和。右边图形中有24个 和6个
半格,面积等于(24+6÷2)个 的
面积和。
三、典例精讲
点评
解答
本题考查面积的认识以及用数格子求不
规则图形面积的方法,关键是正确数出
整数格数和半格数。
面积的认识和面积单位
考点01
解:14+4÷2
=14+2
=16(个)
24+6÷2
=24+3
=27(个)
如图:
三、典例精讲
分析
变式②
(1)4平方分米=400平方厘米,40平方厘米<400平方厘米.
(2)9平方米=90000平方厘米,90000平方厘米>900平方厘米.
(3)5平方米=500平方分米,150平方分米<500平方分米.
(4)8平方分米=800平方厘米,790平方厘米<800平方厘米.
(5)低级单位平方厘米化高级单位平方分米除以进率100,即2100平方厘米=21平方分米.
(6)99平方分米=9900平方厘米,600平方厘米<9900平方厘米.
面积的认识和面积单位
考点01
在〇里填上“>““<”或“=”.
40平方厘米〇4平方分米 9平方米〇900平方厘米
150平方分米〇5平方米 790平方厘米〇8平方分米
2100平方厘米〇21平方分米 600平方厘米〇99平方分米
三、典例精讲
点评
解答
不同单位的名数的大小比较通常是先
化成相同的单位名数,再根据数值的
大小进行比较.平方米、平方分米、
平方厘米相邻单位间的进率是100,
由高级单位化低级单位乘进率,反之
除以进率.
面积的认识和面积单位
考点01
解:
故答案为:<,>,<,<,=,<.
(1)40平方厘米<4平方分米 (2)9平方米>900平方厘米
(3)150平方分米<5平方米 (4)790平方厘米<8平方分米
(5)2100平方厘米=21平方分米 (6)600平方厘米<99平方分米
三、典例精讲
分析
变式③
分别算出每个图形是由多少个小正方形组成的,再比
较即可。
(1)①号是有3个正方形和4个三角形组成的,2个三角形的面
积等于1个正方形的面积,所以①号的面积是5个正方形的面积;
②号的面积是6个正方形的面积;③号是有4个正方形和2个三
角形组成的,2个三角形的面积等于1个正方形的面积,所以③
号的面积是5个正方形的面积;④号是有2个正方形和2个底是2
个格,高是1个格的三角形组成的,这2个三角形的面积等于2
个正方形的面积,所以④号的面积是4个正方形的面积;⑤号
的面积是2个正方形的面积;⑥号的面积是2个三角形的面积,
等于1个正方形的面积;(2)①号是有3个正方形和4个三角形
组成的,2个三角形的面积等于1个正方形的面积,所以①号的
面积是5个正方形的面积;③号是有4个正方形和2个三角形组
成的,2个三角形的面积等于1个正方形的面积,所以③号的面
积是5个正方形的面积;(3)⑥号的面积是2个三角形的面积,
即1个正方形的面积,据此解答即可。
面积的认识和面积单位
考点01
看图填一填。
(1) 号图形的面积最大,是 个 。
(2) 号图形和 号图形的面积相等,是 个 。
(3) 号图形的面积最小,是 个 。
三、典例精讲
点评
解答
本题考查的是面积的认识和大小比较
知识的运用,灵活运用所学的知识是
解答本题的关键。
面积的认识和面积单位
考点01
解:根据分析可知:6>5>4>2>1,即:
(1)②号图形的面积最大,是6个 。
(2)①号图形和③号图形的面积相等,是5个 。
(3)⑥号图形的面积最小,是1个 。
故答案为:(1)②;6;(2)①;③;5;(3)⑥;1。
三、典例精讲
分析
典例02
(1)5平方分米=500平方厘米,500平方厘米>490平方厘米.
(2)24平方米=2400平方厘米.
(3)800平方分米=8平方米,8平方米<9平方米.
(4)1000平方分米=10平方米,10平方米<100平方米.
小面积单位间的进率及单位换算
考点02
填上“>”、“<”或“=”.
5平方分米 490平方厘米
24平方米 2400平方分米
800平方分米 9平方米
1000平方分米 100平方米.
三、典例精讲
点评
解答
不同单位的名数的大小比较通常是先
化成相同的单位名数,再根据整数或
小数或分数的大小比较方法进行比较.
化成什么单位要灵活掌握.
小面积单位间的进率及单位换算
考点02
解:(1)5平方分米>490平方厘米;
(2)24平方米=2400平方分米;
(3)800平方分米<9平方米;
(4)1000平方分<100平方米.
故答案为:>,=,<,<.
三、典例精讲
分析
变式①
根据长方形的面积计算公式“长方形
面积=长×宽”,求出走廊的面积是
多少平方米,然后把平方米化成平方
分米;再根据正方形的面积公式“正
方形面积=边长×边长”求出地砖的
面积,然后用走廊的面积除以正方形
地砖的面积,即可得到需要的块数。
小面积单位间的进率及单位换算
考点02
解答
点评
此题考查的知识点:长方形面积的计
算、正方形面积的计算、面积的单位
换算、整数除法的应用。
解:60米=600分米,2米=20分米
(600×20)÷(2×2)
=12000÷4
=3000(块)
答:需要3000块方砖。
实验小学要在教学楼的一条走廊里铺方砖,这条走廊长60米、宽2米,
用边长2分米的正方形方砖铺地,需要多少块方砖?
三、典例精讲
分析
变式②
(1)5平方分米=500平方厘米,50平方
厘米<500平方厘米,即50平方厘米<5
平方分米.(2)60平方米=6000平方分
米,6000平方分米>60平方分米,即60
平方米>60平方分米.(3)7平方分米=
700平方厘米,780平方厘米>700平方厘
米,即780平方厘米>7平方分米.(4)
低级单位平方分米化高级单位平方米除以
进率100,即400平方分米=4平方米.
小面积单位间的进率及单位换算
考点02
在〇里填上“>”“<”或“=”.
50平方厘米〇5平方分米
60平方米〇60平方分米
780平方厘米〇7平方分米
400平方分米〇4平方米
点评
解答
不同单位的名数的大小比较通常是先化成
相同的单位名数,再根据数值的大小进行
比较.
解:(1)50平方厘米<5平方分米
(2)60平方米>60平方分米
(3)780平方厘米>7平方分米
(4)400平方分米=4平方米.
故答案为:<,>,>,=.
三、典例精讲
分析
变式③
根据正方形的面积=边长×边长求出
面积是多少平方分米,然后根据1平
方米=100平方分米进行判断即可。
小面积单位间的进率及单位换算
考点02
我们已经学习了“1m2=100dm2”,这个关系是如何推导出来的呢?
请你用文字、画图或计算说明推导过程。
点评
解答
本题考查了平方米和平方分米之间的
关系推导过程。
解:如果正方形的边长是1米,面积就是1×1=1(平方米)
因为1米=10分米,所以10×10=100(平方分米),因此1平方米=
100平方分米。
三、典例精讲
分析
典例03
根据平移的知识,剩下部分的面积等
于大正方形的面积减去小长方形的面
积。
长方形、正方形的面积
考点03
解答
解:10×10﹣6×4
=100﹣24
=76(平方厘米)
答:剩下部分的面积是76平方厘米。
点评
熟练掌握长方形和正方形面积公式,
是解答此题的关键。
如图,在一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米
的长方形,剩下部分的面积是多少?
三、典例精讲
分析
变式①
长方形的面积=长×宽,则长方形的长
为400÷8=50(米),扩大后的绿地
宽为32米,长不变,据此计算出扩大
后长方形的面积即可。
长方形、正方形的面积
考点03
解答
解:400÷8=50(米)
50×32=1600(平方米)
答:扩大后的绿地面积是1600平方米。
点评
本题考查了长方形面积公式的灵活运
用,结合题意分析解答即可。
如图,一块长方形绿地面积为400平方米,如果长不变,宽增加到32米,
扩大后的绿地面积是多少平方米?
三、典例精讲
分析
变式②
长方形的长=面积÷宽,现在的宽是
6+24=30(米),根据长方形面积
=长×宽,可求出扩建后的面积。
长方形、正方形的面积
考点03
解答
点评
此题考查长方形面积公式的灵活应用。
解:180÷6=30(米)
6+24=30(米)
30×30=900(平方米)
答:扩建后菜地的面积是900平方米。
王爷爷家有一块长方形菜地(如图),面积是180平方米。现在准备扩
建,长不变,宽增加了24米。扩建后菜地的面积是多少平方米?
三、典例精讲
分析
变式③
根据题意可知,可以围成边长是1厘
米、边长是5厘米、边长是(5+1)
厘米、边长是8厘米、边长是(8+1)
厘米、边长是(5+8)厘米、边长是
(1+5+8)厘米的正方形,根据正
方形的面积=边长×边长,把数据代
入公式解答。
长方形、正方形的面积
考点03
有8厘米、5厘米和1厘米长的小棒各4根,从中选出若干根,并使它们首
尾相接,你能围成多少种大小不同的正方形?围成正方形的面积分别是
多少?请在下表列举不同的围法。
边长/厘米
面积/平方厘米
三、典例精讲
点评
解答
此题考查的目的是理解掌握正方形的
特征及应用,正方形的面积公式及应
用,关键是熟记公式。
长方形、正方形的面积
考点03
解:1+5=6(厘米)
1+8=9(厘米)
5+8=13(厘米)
1+5+8=14(厘米)
答:一共有7种不同的围法。
填表如下:
谢谢观看~
