第五单元 认识方程(复习课件)-四年级数学下学期期末核心考点集训(北师大版)(共22张PPT)
文档属性
| 名称 | 第五单元 认识方程(复习课件)-四年级数学下学期期末核心考点集训(北师大版)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 15:01:52 | ||
图片预览








文档简介
(共22张PPT)
第五单元 认识方程
四年级下册 北师大版
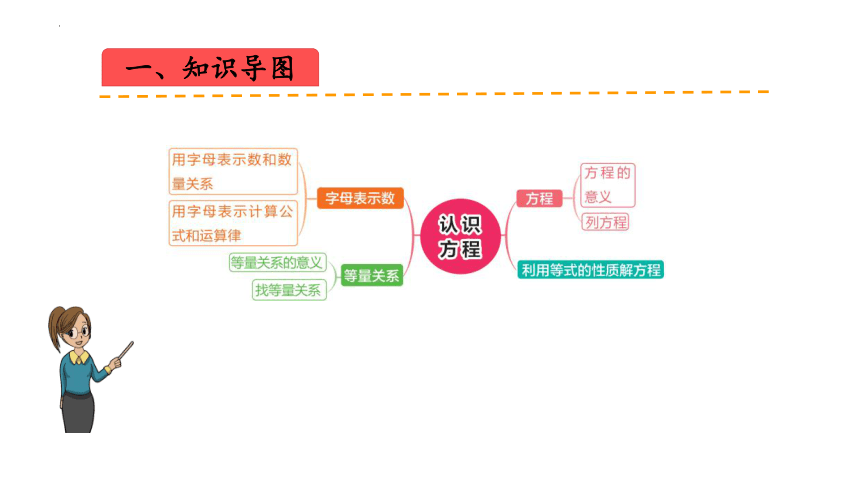
一、知识导图
二、考点梳理
知识点① 用字母表示数
含有字母的式子既可以表示数量关系,也可以表示结果。
二、考点梳理
知识点② 用字母表示运算律
1.如果用a、b、c表示三个数,则可以用字母来表示学过的运算律。
2.字母和字母相乘,中间的乘号可以省略不写;字母和数相乘,中间的乘号也可以
省略不写,数在前字母在后。
二、考点梳理
知识点③ 方程的含义
含有未知数的等式叫方程。
二、考点梳理
知识点④ 等式的性质
1.等式两边都加上或减去同一个数,等式仍然成立。
2.等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立。
二、考点梳理
知识点⑤ 解形如ax±b=c(a≠0)的方程
解形如ax±b=c(a≠0)的方程,步骤如下:
ax±b=c
解: ax±b b=c b
ax=c b
x=(c b)÷a
三、典例精讲
分析
典例01
用总长度减去已经铺了的长度,就是
剩下的长度,再把x=350代入求值
即可。
用字母表示数和运算律
考点01
解答
点评
能用字母表示数量关系,是解答此题
的关键。
铺设一条长3千米的自来水管道,已经铺了8天,每天铺x米。
(1)用含有字母的式子表示未铺的米数。
(2)当x=350时,还剩多少米没有铺?
解:(1)3千米=3000米
3000﹣8x
答:还剩(3000﹣8x)米没有铺。
(2)3000﹣350×8
=3000﹣2800
=200(米)
答:还剩200米没有铺。
三、典例精讲
分析
变式①
(1)根据题意可知,哥哥扛的袋数×每袋的
千克数+弟弟扛的袋数×每袋的千克数=两
兄弟扛的总千克数,用8x+5x即可求出兄弟
俩一共扛了多少千克,再化简即可;
(2)根据题意可知,哥哥扛的袋数×每袋的
千克数﹣弟弟扛的袋数×每袋的千克数=哥
哥比弟弟多扛的千克数,用8x﹣5x即可求出
哥哥比弟弟多扛的千克数,再把x=35代入
计算即可。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及含
未知数式子的化简和求值,找到相应
的数量关系式是解答本题的关键。
哥哥和弟弟帮王奶奶家秋收,每袋稻谷x千克,哥哥扛了8袋,弟弟扛了
5袋。
(1)兄弟俩一共扛了多少千克?(用含有字母的式子表示)
(2)当x=35时,哥哥比弟弟多扛了多少千克?
解:(1)8x+5x=13x(千克)
答:兄弟俩一共扛了13x千克。
(2)8x﹣5x=3x(千克)
当x=35时,
3×35=105(千克)
答:哥哥比弟弟多扛了105千克。
三、典例精讲
分析
变式②
(1)根据总价=单价×数量求出买4
个文具盒的钱数;再将买4个文具盒
和一盒水彩笔的钱数相加,即可得解;
(2)将a=8,b=24代入所得的式
子中,计算即可得解。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及汉
字母式子求值,要熟练掌握。
解:(1)4×a+b=(4a+b)元
(2)当a=8,b=24时
4×8+24=32+24=56(元)
答:王老师一共用去56元钱。
(1)王老师买了4个文具盒和一盒水彩笔,请用含有字母的式子表示王老师用的钱数。
(2)当a=8,b=24时,王老师一共用去多少钱?
三、典例精讲
分析
变式③
(1)由题意可知:甲5小时行驶的
路程与乙5小时行驶的路程之和,就
是两城的距离,用“相遇时间×速度
和=路程”即可列式。
(2)运用字母表示出甲乙两地的距
离,把a=80,b=75代入式子进行
计算即可。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及含
未知数式子的化简和求值,找到相应
的数量关系式是解答本题的关键。
解:(1)a×5+b×5=5a+5b(千米)
答:甲、乙两地间的距离(5a+5b)千米。
(2)5a+5b
当a=80,b=75时
5×80+5×75=400+375=775(千米)
答:甲、乙两地间的距离是775千米。
两辆汽车同时从甲、乙两地相向开出,快车每小时行a千米,慢车每小
时行b千米,经过5小时,两车相遇。
(1)用含有字母的式子表示甲、乙两地间的距离。
(2)当a=80,b=75时,甲、乙两地间的距离是多少千米?
三、典例精讲
分析
典例02
设中间的奇数是x,则这3个连续的奇
数分别为x﹣2,x,x+2,然后根据
题意列出方程解答即可。
等式的性质、方程的含义及解方程
考点02
解答
解:设中间的奇数是x,则这3个连续的奇数分别为x﹣2,x,x+2。
x﹣2+x+x+2=2007
3x=2007
x=669
669﹣2=667
669+2=671
答:这三个数分别是669、669、671。
点评
了解自然数中,奇数的排列规律是完
成本题的关键。
3个连续奇数的和是2007,这三个数分别是多少?(列方程解)
三、典例精讲
分析
变式①
根据图意可知,玉米的质量是小麦质
量的4倍,即为4x,根据小麦的质量
+玉米的质量=180吨,列方程,即
可解答。
等式的性质、方程的含义及解方程
考点02
解答
点评
本题考查列方程解决实际问题。理解
题意,找出数量关系,列等量关系式
是解决本题的关键。
解:x+4x=180
5x=180
5x÷5=180÷5
x=36
答:小麦重36千克。
看图列式解答。
三、典例精讲
分析
变式②
根据等式的性质,可得:24÷x=3
(x>0),那么24÷x×x=3x。
等式的性质、方程的含义及解方程
考点02
如果24÷x=3(x>0),那么24÷x×x=3x。 .
说理: .
点评
解答
此题主要考查了根据等式的性质解方
程的能力,即等式两边同时加上或同
时减去、同时乘或同时除以一个数
(0除外),两边仍相等。
解:如果24÷x=3(x>0),
那么24÷x×x=3x。√
说理:等式两边同时加上或同时减去、同时乘或同时除以一个数(0除
外),两边仍相等。
故答案为:√,等式两边同时加上或同时减去、同时乘或同时除以一个
数(0除外),两边仍相等。
三、典例精讲
分析
变式③
①依据等式的性质,方程两边同时加
35,再同时除以6求解;
②依据等式的性质,方程两边同时加
72,再同时除以3求解;
③依据等式的性质,方程两边同时除
以8,两边同时加12,再同时除以5
求解;
④依据等式的性质,方程两边同时乘
2,两边同时加3x,两边同时减去16,
再同时除以3求解.
等式的性质、方程的含义及解方程
考点02
解下列方程式.
6x﹣35=13;
3x﹣12×6=6;
(5x﹣12)×8=24;
(100﹣3x)÷2=8.
三、典例精讲
点评
解答
此题考查了运用等式的性质解方程,
即等式两边同加上或同减去、同乘上
或同除以一个数(0除外),两边仍
相等,同时注意“=”上下要对齐.
等式的性质、方程的含义及解方程
考点02
解:①6x﹣35=13
6x﹣35+35=13+35
6x=48
6x÷6=48÷6
x=8
②3x﹣12×6=6
3x﹣72+72=6+72
3x=78
3x÷3=78÷3
x=26
三、典例精讲
点评
解答
此题考查了运用等式的性质解方程,
即等式两边同加上或同减去、同乘上
或同除以一个数(0除外),两边仍
相等,同时注意“=”上下要对齐.
等式的性质、方程的含义及解方程
考点02
③(5x﹣12)×8=24
(5x﹣12)×8÷8=24÷8
5x﹣12=3
5x﹣12+12=3+12
5x=15
5x÷5=15÷5
x=3
④(100﹣3x)÷2=8
(100﹣3x)÷2×2=8×2
100﹣3x=16
100﹣3x+3x=16+3x
16+3x﹣16=100﹣16
3x=84
3x÷3=84÷3
x=28
三、典例精讲
分析
典例03
我们设一只燕子每天吃害虫x只,从
而表示出一只青蛙每天吃害虫的只数,
即(2x﹣20)只,等于80只.列方
程解答.
一只青蛙每天吃80只害虫,比一只燕子吃的2倍少20只,一只燕子每天
吃多少只害虫?
列方程解应用题(两步需要逆思考)
考点03
解答
解:设一只燕子每天吃害虫x只.
2x﹣20=80
2x﹣20+20=80+20
2x=100
2x÷2=100÷2
x=50
答;一只燕子每天吃害虫50只.
点评
本题是逆思维题,运用方程解答便于
理解,设出一个量表示出另一个量,
列方程解答即可.
三、典例精讲
分析
变式①
s根据池塘里鸭子比岸上鸭子只数的3
倍少12只,可知本题的数量关系:岸
上的鸭子数×3﹣12=池塘里的鸭子.
据此等量关系可列方程解答.
列方程解应用题(两步需要逆思考)
考点03
解答
解:设岸上有x只鸭子,根据题意得
3x﹣12=30,
3x﹣12+12=30+12,
3x÷3=42÷3,
x=14.
答:岸上有14只鸭子.
点评
本题的关键是找出题目中的数量关系,
再列方程解答.
池塘里有鸭子30只,比岸上鸭子只数的3倍少12只,岸上有多少只鸭子?
(用方程解答)
三、典例精讲
分析
变式②
设野兔奔跑的速度是每小时x千米,
则非洲鸵鸟的奔跑速度为每小时2x﹣
12千米,根据非洲鸵鸟的奔跑速度
列方程解答即可.
列方程解应用题(两步需要逆思考)
考点03
解答
点评
本题考查了列方程解应用题,关键是
根据非洲鸵鸟的奔跑速度列方程.
解:设野兔奔跑的速度是每小时x千米,
2x﹣12=72
2x=84
x=42
答:野兔奔跑的速度是每小时42千米.
非洲鸵鸟的奔跑速度可达每小时72千米,比野兔的2倍少12千米,野兔
奔跑的速度是每小时多少千米?(用方程解)
三、典例精讲
分析
变式③
先设湿地鸟类有x种,可以列出等量
关系式为8x+178=2258,据此解答。
列方程解应用题(两步需要逆思考)
考点03
解答
解:设湿地鸟类有x种。
8x+178=2258
8x=2080
x=260
答:湿地鸟类有260种。
点评
此题考查了学生对列方程、解方程的
熟练掌握程度。关键是找出等量关系
式。
截至2022年1月,我国的国际重要湿地生态状况总体保持稳定,其中湿
地植物2258种,比湿地鸟类的8倍多178种。湿地鸟类有多少种?(先
列出等量关系,再列方程解答)
谢谢观看~
第五单元 认识方程
四年级下册 北师大版
一、知识导图
二、考点梳理
知识点① 用字母表示数
含有字母的式子既可以表示数量关系,也可以表示结果。
二、考点梳理
知识点② 用字母表示运算律
1.如果用a、b、c表示三个数,则可以用字母来表示学过的运算律。
2.字母和字母相乘,中间的乘号可以省略不写;字母和数相乘,中间的乘号也可以
省略不写,数在前字母在后。
二、考点梳理
知识点③ 方程的含义
含有未知数的等式叫方程。
二、考点梳理
知识点④ 等式的性质
1.等式两边都加上或减去同一个数,等式仍然成立。
2.等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立。
二、考点梳理
知识点⑤ 解形如ax±b=c(a≠0)的方程
解形如ax±b=c(a≠0)的方程,步骤如下:
ax±b=c
解: ax±b b=c b
ax=c b
x=(c b)÷a
三、典例精讲
分析
典例01
用总长度减去已经铺了的长度,就是
剩下的长度,再把x=350代入求值
即可。
用字母表示数和运算律
考点01
解答
点评
能用字母表示数量关系,是解答此题
的关键。
铺设一条长3千米的自来水管道,已经铺了8天,每天铺x米。
(1)用含有字母的式子表示未铺的米数。
(2)当x=350时,还剩多少米没有铺?
解:(1)3千米=3000米
3000﹣8x
答:还剩(3000﹣8x)米没有铺。
(2)3000﹣350×8
=3000﹣2800
=200(米)
答:还剩200米没有铺。
三、典例精讲
分析
变式①
(1)根据题意可知,哥哥扛的袋数×每袋的
千克数+弟弟扛的袋数×每袋的千克数=两
兄弟扛的总千克数,用8x+5x即可求出兄弟
俩一共扛了多少千克,再化简即可;
(2)根据题意可知,哥哥扛的袋数×每袋的
千克数﹣弟弟扛的袋数×每袋的千克数=哥
哥比弟弟多扛的千克数,用8x﹣5x即可求出
哥哥比弟弟多扛的千克数,再把x=35代入
计算即可。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及含
未知数式子的化简和求值,找到相应
的数量关系式是解答本题的关键。
哥哥和弟弟帮王奶奶家秋收,每袋稻谷x千克,哥哥扛了8袋,弟弟扛了
5袋。
(1)兄弟俩一共扛了多少千克?(用含有字母的式子表示)
(2)当x=35时,哥哥比弟弟多扛了多少千克?
解:(1)8x+5x=13x(千克)
答:兄弟俩一共扛了13x千克。
(2)8x﹣5x=3x(千克)
当x=35时,
3×35=105(千克)
答:哥哥比弟弟多扛了105千克。
三、典例精讲
分析
变式②
(1)根据总价=单价×数量求出买4
个文具盒的钱数;再将买4个文具盒
和一盒水彩笔的钱数相加,即可得解;
(2)将a=8,b=24代入所得的式
子中,计算即可得解。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及汉
字母式子求值,要熟练掌握。
解:(1)4×a+b=(4a+b)元
(2)当a=8,b=24时
4×8+24=32+24=56(元)
答:王老师一共用去56元钱。
(1)王老师买了4个文具盒和一盒水彩笔,请用含有字母的式子表示王老师用的钱数。
(2)当a=8,b=24时,王老师一共用去多少钱?
三、典例精讲
分析
变式③
(1)由题意可知:甲5小时行驶的
路程与乙5小时行驶的路程之和,就
是两城的距离,用“相遇时间×速度
和=路程”即可列式。
(2)运用字母表示出甲乙两地的距
离,把a=80,b=75代入式子进行
计算即可。
用字母表示数和运算律
考点01
解答
点评
本题主要考查了用字母表示数以及含
未知数式子的化简和求值,找到相应
的数量关系式是解答本题的关键。
解:(1)a×5+b×5=5a+5b(千米)
答:甲、乙两地间的距离(5a+5b)千米。
(2)5a+5b
当a=80,b=75时
5×80+5×75=400+375=775(千米)
答:甲、乙两地间的距离是775千米。
两辆汽车同时从甲、乙两地相向开出,快车每小时行a千米,慢车每小
时行b千米,经过5小时,两车相遇。
(1)用含有字母的式子表示甲、乙两地间的距离。
(2)当a=80,b=75时,甲、乙两地间的距离是多少千米?
三、典例精讲
分析
典例02
设中间的奇数是x,则这3个连续的奇
数分别为x﹣2,x,x+2,然后根据
题意列出方程解答即可。
等式的性质、方程的含义及解方程
考点02
解答
解:设中间的奇数是x,则这3个连续的奇数分别为x﹣2,x,x+2。
x﹣2+x+x+2=2007
3x=2007
x=669
669﹣2=667
669+2=671
答:这三个数分别是669、669、671。
点评
了解自然数中,奇数的排列规律是完
成本题的关键。
3个连续奇数的和是2007,这三个数分别是多少?(列方程解)
三、典例精讲
分析
变式①
根据图意可知,玉米的质量是小麦质
量的4倍,即为4x,根据小麦的质量
+玉米的质量=180吨,列方程,即
可解答。
等式的性质、方程的含义及解方程
考点02
解答
点评
本题考查列方程解决实际问题。理解
题意,找出数量关系,列等量关系式
是解决本题的关键。
解:x+4x=180
5x=180
5x÷5=180÷5
x=36
答:小麦重36千克。
看图列式解答。
三、典例精讲
分析
变式②
根据等式的性质,可得:24÷x=3
(x>0),那么24÷x×x=3x。
等式的性质、方程的含义及解方程
考点02
如果24÷x=3(x>0),那么24÷x×x=3x。 .
说理: .
点评
解答
此题主要考查了根据等式的性质解方
程的能力,即等式两边同时加上或同
时减去、同时乘或同时除以一个数
(0除外),两边仍相等。
解:如果24÷x=3(x>0),
那么24÷x×x=3x。√
说理:等式两边同时加上或同时减去、同时乘或同时除以一个数(0除
外),两边仍相等。
故答案为:√,等式两边同时加上或同时减去、同时乘或同时除以一个
数(0除外),两边仍相等。
三、典例精讲
分析
变式③
①依据等式的性质,方程两边同时加
35,再同时除以6求解;
②依据等式的性质,方程两边同时加
72,再同时除以3求解;
③依据等式的性质,方程两边同时除
以8,两边同时加12,再同时除以5
求解;
④依据等式的性质,方程两边同时乘
2,两边同时加3x,两边同时减去16,
再同时除以3求解.
等式的性质、方程的含义及解方程
考点02
解下列方程式.
6x﹣35=13;
3x﹣12×6=6;
(5x﹣12)×8=24;
(100﹣3x)÷2=8.
三、典例精讲
点评
解答
此题考查了运用等式的性质解方程,
即等式两边同加上或同减去、同乘上
或同除以一个数(0除外),两边仍
相等,同时注意“=”上下要对齐.
等式的性质、方程的含义及解方程
考点02
解:①6x﹣35=13
6x﹣35+35=13+35
6x=48
6x÷6=48÷6
x=8
②3x﹣12×6=6
3x﹣72+72=6+72
3x=78
3x÷3=78÷3
x=26
三、典例精讲
点评
解答
此题考查了运用等式的性质解方程,
即等式两边同加上或同减去、同乘上
或同除以一个数(0除外),两边仍
相等,同时注意“=”上下要对齐.
等式的性质、方程的含义及解方程
考点02
③(5x﹣12)×8=24
(5x﹣12)×8÷8=24÷8
5x﹣12=3
5x﹣12+12=3+12
5x=15
5x÷5=15÷5
x=3
④(100﹣3x)÷2=8
(100﹣3x)÷2×2=8×2
100﹣3x=16
100﹣3x+3x=16+3x
16+3x﹣16=100﹣16
3x=84
3x÷3=84÷3
x=28
三、典例精讲
分析
典例03
我们设一只燕子每天吃害虫x只,从
而表示出一只青蛙每天吃害虫的只数,
即(2x﹣20)只,等于80只.列方
程解答.
一只青蛙每天吃80只害虫,比一只燕子吃的2倍少20只,一只燕子每天
吃多少只害虫?
列方程解应用题(两步需要逆思考)
考点03
解答
解:设一只燕子每天吃害虫x只.
2x﹣20=80
2x﹣20+20=80+20
2x=100
2x÷2=100÷2
x=50
答;一只燕子每天吃害虫50只.
点评
本题是逆思维题,运用方程解答便于
理解,设出一个量表示出另一个量,
列方程解答即可.
三、典例精讲
分析
变式①
s根据池塘里鸭子比岸上鸭子只数的3
倍少12只,可知本题的数量关系:岸
上的鸭子数×3﹣12=池塘里的鸭子.
据此等量关系可列方程解答.
列方程解应用题(两步需要逆思考)
考点03
解答
解:设岸上有x只鸭子,根据题意得
3x﹣12=30,
3x﹣12+12=30+12,
3x÷3=42÷3,
x=14.
答:岸上有14只鸭子.
点评
本题的关键是找出题目中的数量关系,
再列方程解答.
池塘里有鸭子30只,比岸上鸭子只数的3倍少12只,岸上有多少只鸭子?
(用方程解答)
三、典例精讲
分析
变式②
设野兔奔跑的速度是每小时x千米,
则非洲鸵鸟的奔跑速度为每小时2x﹣
12千米,根据非洲鸵鸟的奔跑速度
列方程解答即可.
列方程解应用题(两步需要逆思考)
考点03
解答
点评
本题考查了列方程解应用题,关键是
根据非洲鸵鸟的奔跑速度列方程.
解:设野兔奔跑的速度是每小时x千米,
2x﹣12=72
2x=84
x=42
答:野兔奔跑的速度是每小时42千米.
非洲鸵鸟的奔跑速度可达每小时72千米,比野兔的2倍少12千米,野兔
奔跑的速度是每小时多少千米?(用方程解)
三、典例精讲
分析
变式③
先设湿地鸟类有x种,可以列出等量
关系式为8x+178=2258,据此解答。
列方程解应用题(两步需要逆思考)
考点03
解答
解:设湿地鸟类有x种。
8x+178=2258
8x=2080
x=260
答:湿地鸟类有260种。
点评
此题考查了学生对列方程、解方程的
熟练掌握程度。关键是找出等量关系
式。
截至2022年1月,我国的国际重要湿地生态状况总体保持稳定,其中湿
地植物2258种,比湿地鸟类的8倍多178种。湿地鸟类有多少种?(先
列出等量关系,再列方程解答)
谢谢观看~
